Laboratory investigation of gas permeability and its impact on CBM potential

Abstract

Gas permeability is an important characteristic of coal seam(s) to determine the economic success of CH₄ extraction and CO₂ sequestration. There exists no comprehensive approach to predict the mechanical behaviour during CH₄ extraction, and CO₂ sequestration as coal is highly heterogeneous. Exhaustive laboratory experimentation is often the only approach to successfully predict its behaviour. Coal experiences triaxial stress conditions when change of force field occurs. This paper presents the mechanical properties and change in gas permeability at varying confining as well as gas pressures in a triaxial experimental set-up using Darcy’s approach. Mutual relations between permeability, in situ confining pressure as well as gas pressure have been established statistically. A reservoir simulation investigation has been carried out to predict the rate of coal bed methane (CBM) production and the cumulative amount of CBM over the 5-year life of production well.

Introduction

Coal permeability, porosity, cleat structure, adsorption/desorption of gases, in situ stress–strain of coal matrix are major parameters that influence CBM production and CO₂ sequestration. Permeability gives the general outlook of the flow behaviour of gases in coal matrix. Percentage of gas saturation, gas rate and recoverability of gas from a reservoir is mainly determined by adsorption/desorption behaviour and permeability of coal. Planning a successful pilot as well as production wells depends on the permeability characteristics in coal (Moore 2012). It is an important parameter necessary to model gas flow behaviour in the reservoir. The successful and economic growth of CBM production needs to advance knowledge of coal structural properties and their variation under in situ conditions (Holloway 1997; White 2005). The coal seams are extremely heterogeneous reservoirs whose permeability depends not only on geological age, coal rank and purity, but also on gas and water saturations, in situ stresses and sorbed gas content. The natural fractures and cracks are commonly observed in all rock types but is perhaps most prominent in sedimentary rocks like coal (McCulloch et al. 1974). The fracture plane in flat-lying strata is usually perpendicular to the bedding plane commonly called cleats or cleat surfaces. The coal tends break along the cleat direction (the face cleat, also known as main or master cleat, and butt cleat, also known as cross or board cleat). There exist many reports that predict the seam behaviour post-production from the determination of permeability in the laboratory using triaxial condition (Xiao et al. 2005; Yang and Zoback 2011; Wang et al. 2012; Perera and Ranjith 2012; Zheng et al. 2012; Zhu et al. 2013; Ghanizadeh et al. 2014; Maffucci et al. 2015). Laboratory-measured permeability anisotropies exhibited 2:1 contrast in the face and butt cleats and a 100:1 contrast between face cleat and vertical permeability (Gash et al. 1993). The same 2:1 ratio of face cleat to butt cleat permeabilities was also observed in an interference test in San Juan coals (Mavor and Robinson 1993). Horizontal permeability anisotropy of 17:1 was reported from an interference test in the Warrior Basin (Koenig and Stubbs 1986). The permeability in the horizontal direction is about 42 times than that in the vertical direction (Young et al. 1991). Coal matrix permeability is on the order of micro-darcies or nanodarcies, while coal cleat permeabilities range between 0.1 and 1000 mD (Bell and Rakop 1986). Coal seam permeability decreases exponentially with effective in situ vertical stress (Chatterjee et al. 2010). Gas release from the matrix appears to be diffusive that follows Fick’s law (Seidle 2011). Coal matrix and cleat permeability govern fluid flow through a coal seam. Gas permeability depends on in situ pressure at the seam, i.e. the higher vertical pressure would exhibit reduced permeability and a delayed recovery (Shi and Durucan 2005). Coal bed methane (CBM) production significantly depends on the outcome of the permeability forecast that depends on pore pressure (Robertson and Christiansen 2006). Decreased permeability was reported for coal samples as the high confining pressure closed internal fractures (Siriwardane et al. 2009). It was also observed that the bridge across fractures influences the gas permeability at varying pressures (Izadi et al. 2011). Permeability increased continuously with decrease in pore pressure and absolute value of cleat compressibility increased with decreasing pore pressure (Liu et al. 2012). The macro-diffusivity decreased by more than 82% from dry coal to wet coal and reduced by 73% in case of CO₂ and by 88% for in case of CH₄ (Pan et al. 2010). It was found that with CO₂ injection both (matrix and fracture) permeabilities decreased, but the reductions in fracture permeability were more dramatic than that in the matrix permeability (Wu et al. 2011). Permeability is the most important attribute controlling gas flow in a coal seam reservoir and is influenced by depth, stress regime within the basin and the organic composition of the coal (Moore 2012). The permeability was found to increase continuously with a decrease in pore pressure from 7.6 to ~ 0.35 MPa. The rate of increase in permeability was insignificant between 7.6 and 3.5 MPa and became significant below 3.5 MPa (Liu and Harpalani 2012). The coal permeability depends on the coal fractures controlled by strata stress and gas pressure which changes with depth (Guo and Cheng 2013).

This paper investigated the coal characteristics and gas permeability of coal from different parts of Jharia coal basin, India. Laboratory experiments were carried out to simulate in situ conditions including varying confinements. The correlation of different geo-mechanical parameters with permeability was established using statistical methods. Reservoir simulation was carried out to predict the gas production rate as well as cumulative gas volume over the life of production well.

Geological setting of Jharia coal bed basin

Jharia coal bed basin is located in Dhanbad district of Jharkhand, India. It is bounded between 23°37′N and 23°52′N and longitudes 86°05′E and 86°30′E (Fig. 1). It covers an area of 465 km² extending along the east–west direction (Saikia and Sarkar 2007). The thick sedimentary sequence began with the glacigenic sediments of the Talchir Formation and extended up to Raniganj formations (Ghosh et al. 2014). Barakar Formation comprises 18 standard coal horizon (numbered I to XVIII) with the thickness of each horizon ranging from 1.2 to 29.29 m. Maximum coal seam in this area is reported to be the virgin (Ghosh et al. 2014). Coal block lithology in Barakar Formation covers an area of 20.63 km². Underground mining activities are predominant in this area varying from 200 to 650 m from surface. Mostly these mines are full of the gassy environment with elevated strata temperature (Ghosh et al. 2014). Gas in place of Jharia coal field varies from 2 to 16 m³/ton (daf basis) (CMPDI 2015). Overall estimated gas in place comes to about 7970.47 million cubic meters (CMPDI 2015) (Table 1).

Fig. 1

Geological map and lithology of the Jharia Coalfield showing Moonidih coal block (Modified after Ghosh et al. 2014; BCCL 2012)

Table 1 Seam-wise estimated CBM in Moonidih coalfield (CMPDI 2015)

Sample collection

Sample collection and preservation are the primary requirements for accurate deterministic estimation of coal properties. In this study, the rectangular coal blocks were collected from freshly exposed coal surface of Jharia coal field (Moonidih area), Jharkhand, India, at the depths varying from 400 to 580 m. Coal blocks were collected at right angle to bedding plane of the coal seam. Coal blocks were sealed to preserve natural conditions. Collected and covered samples were brought to the laboratory with care.

Sample preparation

Coal characterization

The laboratory experiments involved for the determination of coal characteristics as proximate and ultimate analyses as well as physico-mechanical properties. Coal samples were crushed and ground to 212 µ size for proximate and ultimate analyses as per guideline [IS: 436 (Part l/Section 1)—1964]. Powdered samples were collected and kept in clean air-dried plastic bag for testing purpose. Coring was carried out as per [IS: 9179–1979, Reaffirmed 2001] [ASTM: D2113, 2014] (Fig. 2a). The polished cores were wrapped with rubber jacket and sealed with plastic tape for permeability testing (Fig. 2b).

Fig. 2

a Unrapped sample showing cleats, b wrapped sample for permeability testing

Apparatus and procedure

Measurement of permeability

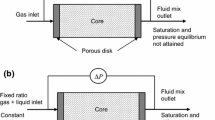
One of the most convenient methods for the determination of permeability of coal at in situ condition in the laboratory is to apply a uniform hydraulic pressure to the curved surface of a cylindrical specimen and then to apply an axial compressive force simultaneously with passing gas through the specimen until failure occurs (Figs. 3, 4). Compression testing machine (Make: Aimil Ltd.) of 1000 kN was used for application of vertical load, while confining pressure was provided using constant pressure system (Make: Aimil Ltd.). Hoek cell (Make: ELE Int., UK) of internal diameter 54 mm was used for holding core sample of diameter 54 mm with L/D ratio 2. In this system, vertical force was applied to the specimen using perforated pedestals (Pistons) made up of cast iron (G2 grade). The specimen was placed inside the Hoek cell and sealed by top and base pedestals. The pedestals were perforated to pass gas along with the application of vertical load. The load was applied by the upward movement of compression testing machine. Gas flow line starts from the inlet port which is connected to the gas cylinder using hose connection. The opening of valves 1 and 2 makes gas to pass into gas flow line and gets stored in reference cell up to predefined pressure. Once the predefined pressure is achieved, the valves 1 and 2 are closed, and valve 3 is opened to flow gas through the upper piston. Gas was flown to specimen through the upper piston continuously until the saturation achieved. The opening of valve 4 allowed gas to be stored in reference cell 2. Pressure gauge 3 indicated the gas pressure in reference cell 2. Gas in reference cell 2 was stored up to 3.5 MPa.

Fig. 3

Schematic diagram of gas permeability set-up

Fig. 4

Experimental set-up for coal gas permeability

The procedure for gas permeability testing starts with mounting wrapped coal core sample in the pressure chamber of Hoek cell. The chamber was then sealed with upper and lower pedestals and evacuated to remove air. The system was re-pressurized to a predetermined level and maintained. Methane gas was then passed through coal sample at varying pressures. The released gases from outlet port pass through the measuring system that consists of pressure gauge as well as flowmeter (make: PCI Analytics Pvt. Ltd, Mumbai) of 0–27.5 MPa and 0–15 LPM, respectively. The sequence of permeability testing followed in steps by varying vertical as well as horizontal stresses at a different level.

Permeability and mechanical properties

Gas permeability in coal is usually calculated using Darcy’s equation as:

$$K = \frac{{2Q_{0} \mu Lp_{0} }}{{A\left( {P_{1}^{2} - P_{2}^{2} } \right)}}$$

(1)

where K = coefficient of gas permeability (m²); Q₀ = gas flow rate (m³/s); µ = viscosity of gas (Pa.s); L = length of sample; p₀ = reference pressure (p₀ = P₂); A = cross-sectional area (m²); P₁ and P₂ = upstream and downstream gas pressures, respectively (Pa).

The following assumption is involved using Eq. (1)

• (1) Laminar flow

• (2) Steady-state flow

• (3) Cleats are straight and free from coal particles

• (4) No-slip boundary conditions

• (5) Constant temperature of coal core sample

The flow of methane from coal matrix to well bore was completed in two phases. In the first phase, the adsorbed volume of methane diffuses from coal matrix to the cleat structures through micro-pores and then in the second phase, it flows through the natural fractures or cleat network to the well bore in response to a pressure gradient obeying Darcy’s law.

The Darcy type of flow was observed a laminar viscous flow in which the flow paths are either prismatic or streamlined (Lama and Nguyen 1984). One of the most important consequences of Darcy’s law is that there should not be molecular slippage along the internal wall of the pores. The steady-state laminar flow of gas in fractured network of straight cleat is well described by Darcy’s equation; therefore, Eq. (1) is involved for the determination of permeability in coal sample.

Dual-continuum system, i.e. the porous coal matrix and cleat structure, is an important characteristic of coal seams. The multiphase flow processes in coal matrix showed a considerable effect on coal bed methane recovery processes (Wei et al. 2007). The stress value increases with an addition in depth that causes decrease in permeability of coal matrix. The permeability and stress are exponentially related to each other as (Reiss 1980):

$$\frac{k}{{k_{i} }} = e^{{\left[ { - 3C_{\text{f}} \left( {\sigma_{\text{h}} - \sigma_{\text{hi}} } \right)} \right]}}$$

(2)

where k = permeability, k_i = initial permeability, c_f = cleat compressibility, σ_h = hydrostatic stress, and σ_hi = initial hydrostatic stress.

At the hydrostatic stress, the permeability variation with depth is expressed as (McKee et al. 1988):

$$\frac{k}{{k_{i} }} = e^{{\left[ { - 3C_{\text{f}} \left( {\sigma_{\text{v}} - \sigma_{\text{vi}} } \right)} \right]}}$$

(3)

$$\sigma_{\text{m}} = \frac{{\sigma_{\text{v}} }}{3}\left( {\frac{1 + \upsilon }{1 - \upsilon }} \right)$$

(4)

where σ_m = mean stress, σ_v = vertical stress and ʋ is Poisson’s ratio

The expression for the transformation of laboratory result to the in situ regime condition is:

$$\frac{k}{{k_{i} }} = e^{{\left[ { - C_{\text{f}} \left( {\frac{1 + \upsilon }{1 - \upsilon }} \right)\left( {\sigma_{\text{v}} - \sigma_{\text{vi}} } \right)} \right]}}$$

(5)

The relation between permeability and the depth of the coal seam is:

$$\frac{k}{{k_{i} }} = e^{{\left[ { - C_{\text{f}} \left( {\frac{1 + \upsilon }{1 - \upsilon }} \right) \cdot A\left( {d - d_{i} } \right)} \right]}}$$

(6)

where d = depth and A = constant

Reservoir modelling

The major assumptions involved in the reservoir simulations are:

• The reservoir is homogeneous and isotropic with uniform thickness and constant porosity, permeability and compressibility

• The height of each fracture is equal to that of reservoir

• The gravity force is neglected

• The stress sensitivity of the cleat system is ignored

• The gas diffusivity coefficient is constant

Dual-porosity (Gilman and Kazemi) model and two-phase flow followed by Fick’s law and Darcy’s law were assumed for flow of gas from the matrix block to the fracture block and fracture block to the production well. The simulation was carried out by considering pure CH₄ component-based flow.

Model building

Coal seam JH-MD-S₁ was considered for reservoir simulation and production prediction because of higher depth and gas content of the seam. Coal bed reservoir shows dual-porosity nature due to its stress dependency of coal permeability and porosity, as well as desorption of gas from the matrix and flows through the natural fracture (cleat structure); thus, the reservoir modelling and simulation were performed under dual-porosity settings. The modelling and simulation were carried out using GEM software suite 2015.10. Many models were run to visualize, analyse and understand the CBM production over time.

Grid formulation

Homogeneous Cartesian grid system was applied to develop hypothetical reservoir model. The coal bed reservoir was assumed highly fractured and well-developed cleat network. To represent the well-cleated network with face cleat and butt cleat, total reservoir area (700 × 700 m²) (assumed based on CMPDI Report 2015) was divided into 23 × 24 grids in i and j coordinates of Cartesian grid system. In order to represent close proximity of the cleated network, 23 × 24 grids were assumed. 23 grids in X axis and 24 grids in Y axis were distributed between 700 × 700 m distances, respectively. Six grids were distributed in Z axis over 6 m distance representing the seam thickness of JH-MD-S₁ coal seam at 580 m depth of occurrence (site data) (Fig. 5).

Fig. 5

Grid block with four production wells

Wells and boundary condition

Four-point patterns were considered for distribution of production well in coal seam area for prediction of gas production rate (m³/day) and cumulative gas in place (m³) over time. Production well was made constant surface water rate max. 200 m³/day as well as bottom hole pressure min. 200 kPa. Horizontal fracturing was created on either side of the production well. The coal seam was considered to be sealed and isotropic to focus more on the input parameters. The overburden pressure of 15.66 MPa at 580 m depth was considered as initial vertical pressure. The Langmuir adsorption isotherm was used to model the reservoir condition. The reservoir base model consisting of four wells, with 16 hydraulic fractures spaced 25 m apart, was constructed. The distance between each well was 100 m. The well location is hypothetical, and all dimensions were assumed based on reservoir model described for CBM production elsewhere (CMPDI Report 2015; Makinde and Lee 2016). The constraint for each well was set to the initial hydrostatic pressure at the well location. The fractures are all infinitely conductive. For computational purposes, a fracture spacing of 14.9 mm was used. The initial parameter setting of base model is listed in Table 2.

Table 2 Initial parameter settings in base model

Results and discussion

Coal characterization

Coal characterization is an important factor to understand the composition and maturity of coal (Tables 3 and 4). VM varies from 22.53 to 26.88, while FC was in between 55.64 and 63.18. It indicates the rank of the coal as medium volatile bituminous (Fig. 6). Variation in moisture content from 0.93 to 1.28 also indicates medium-volatile bituminous coal. The content of fixed carbon divided by the content of volatile matter is called the fuel ratio. According to their fuel ratios, coals have been classified as anthracite, at least 10; semi-anthracite, 6–10; semi-bituminous, 3–6; and bituminous, 3 or less. Fuel ratio was observed from 1.59 to 3.26 confirming the bituminous rank of coal (Table 4). A similar observation was described for the determination of US coal rank by the fuel ratio (Frazer 1877). H:C ratio was found to vary from 0.053 to 0.075 that indicates bituminous coal (Table 4). A similar observation was reported in Alabama and Arkansas coal for the determination of maturity of coal elsewhere (Campbell 1904). The value of vitrinite reflectance is calculated using established Rice formula (Rice 1993):

$$R_{0} \left( \% \right) = - 2.712 \times \log \left( {{\text{VM}}_{\text{daf}} } \right) + 5.092$$

(7)

where R₀ = vitrinite reflectance (%), VM (daf) = volatile matter (dry ash-free basis) (%).

Table 3 Proximate analysis of coal samples

Table 4 Results of ultimate analysis and other parameters of coal samples

Fig. 6

Coal rank chart (Averitt and Berryhill 1950)

The highest value of vitrinite reflectance was 1.132 at 520 m depth (Table 3). The range of R₀ values between 0.79 and 1.132 indicates medium-volatile bituminous coal as per rank parameter discussed elsewhere (Diessel 1992). The range of vitrinite reflectance observed in this study lies in between threshold value 0.7–2.0% for commercial CBM prospects as described elsewhere (Chandra 1997) indicating the suitability of CBM production in the study area.

Geo-mechanical characterization

The flow of gas in coal involves complex gas–solid interaction. Geo-mechanical characterization is necessary to determine the elastic deformation behaviour at different gas pressures as well as potential of coal to bear fluid pressure during CBM production. Ten coal core samples from three different seams were used as per [ASTM D7012-14] for the determination of uniaxial compressive strength (UCS), Poisson’s ratio, elastic modulus (E), bulk modulus (K) and modulus of rigidity (G). Average value of three tests was reported (Table 5). UCS was determined under displacement mode at the rate of 0.05 mm/s to obtain post-failure stress–strain curve. Coal sample JH-MD-S₁ at the depth of 580 m showed the lowest compressive strength with lower elastic modulus. But strength increased with decreasing depth of occurrence. The coal specimen strength showed inverse relation with the depth of occurrence. It is because of the increasing presence of pores high in situ gas content.

Table 5 Geo-mechanical properties

Permeability of coal

In this investigation, methane (CH₄) (99.99% purity) was used to pass through the coal core for the determination of permeability of coal. The sample was gas saturated at 3.5 MPa for 10–12 days before conducting the experiment. Horizontal pressure up to 6 MPa with an increment of 0.5–1 MPa at each step was applied on the specimen using hydraulic oil. Vertical pressure up to 10 Mpa with an increment of 1–1.5 MPa at each step was applied. Gas pressure up to 3.5 MPa with an increment of 0.5 MPa at each step was applied. Downstream flow of gas was allowed to determine permeability at different pressure conditions.

Maximum permeability of 0.377, 0.332 and 0.97 mD was obtained for coal samples JH-MD-S₁, JH-MD-S₂ and JH-MD-S₃, respectively. Decreased trend of permeability was observed at increased gas pressure (Figs. 7, 8, 9). It is observed that as gas pressure increases adsorption ability of coal also increases and as a result reduces the porosity of coal. The reduction and closure of pores lead to swelling. Swelling of the coal matrix does not create any fine pores but only inward expansion, and due to it the internal fractures and cleat become narrow, thereby reducing permeability.

Fig. 7

Variation of permeability with gas pressure

Fig. 8

Variation of permeability with gas pressure

Fig. 9

Variation of permeability with gas pressure

The analysis was also carried out to explore the relation between confining pressure and permeability. Change in permeability was observed at confining pressure ranges from 1 to 6 MPa (Figs. 10, 11, 12). Results showed permeability values of all coal samples below 1 mD under confined conditions. It was observed that permeability of coal samples decreased with increased confining pressure. This is attributed due to the closure of pores and reduction in porosity as well as narrowing of fractures influenced by both gas pressure and confinement.

Fig. 10

Correlation of permeability with confining pressure

Fig. 11

Correlation of permeability with confining pressure

Fig. 12

Correlation of permeability with confining pressure

Reduction in permeability was 24.65% for JH-MD-S₁ coal sample, but it was 23.58 and 22.97% for JH-MD-S₂, and JH-MD-S₃ coal samples. Different coals showed different rates of reduction in permeability when subjected to the same level of stress. When a coal specimen was loaded, it underwent structural changes. These changes were dependent on the mechanical strength of coal samples. Coals with a high degree of elasticity and less apparent fractures usually undergone lower reduction in permeability after the application of pressure. Change in permeability was correlated with depth at variable confinement. It was observed that with an increase in depth from 400 to 580 m the percentage of permeability decreased (Fig. 13). Highest permeability change of 40.5% at 2.94 MPa confinement was observed at the depth of 400 m. This is in response to the reduction in the pore throats, subsequently reducing the ability of the porous media to transmit fluids. As the confinement increased, the closure of cleats was fast, and reduction in permeability was rapid. The reduction in permeability was also due to the crushing of the grains or fracture closure. The reduction percentage of permeability was lower with further increase in confinement. With an increase in confinement, the ability of the coal to adsorb gas gradually tends to equilibrium, while the decrease rate of permeability gradually decreases and tends to be gentle. The formation of new cracks and fractures at higher confinement allow gas to flow through it which decreases the reduction percentage of permeability.

Fig. 13

Variation of permeability with depth at varying confining pressures

Equations (2), (3) and (4) are the established models to determine permeability based on the hydrostatic stress, vertical stress as well as mean stress. These models indicate the exponential correlations between permeability and stresses. Figures 7, 8, 9, 10, 11, 12 13 show the correlation plot between permeability and gas pressure as well as confining pressure obtained from the experimental data. The exponential correlations between permeability and confining pressure in these studies satisfy the established model.

Cleat structure and mechanism of gas permeability

Cleats and fractures of coal samples play an extensive role in the production of coal bed methane at economic rates. The preidentification and study of such cleats provide significant information about the extent and frequency of their occurrence through the coal bed and subsequent formulation of an optimal methane gas production strategy. The density, as well as the dimensions of cleats (aperture and spacing), is easily identified using imaging technique. Study of cleats was carried out on core coal samples at the depth of 580 m. The image of the coal core sample was taken using high-resolution 30.4 megapixel DSLR cameras. The image was captured before and after the flow of gas through coal core samples. The size of the natural fracture was measured using KLONK image measurement software. Gas was passed through the coal core sample, and the change in size of natural fracture was measured at varying gas pressures, respectively. Primary and tertiary cleat network was identified on coal core sample (Fig. 14). The cleat spacing of intact coal specimen varied from 0.83 to 2.18 mm indicating well-developed cleats. The cleat network serves as the natural pathway for commercial flow rates of methane through coal seam. Therefore, the frequency of natural fractures, their interconnections, spacing, and gas pressure all affect the permeability. The change in cleat spacing and bulk volume of coal sample was experimentally analysed.

Fig. 14

Cleat network in intact coal sample

Methane was injected increasingly in coal core sample till 4.2 MPa to determine the change in fracture dimension as well as the volume of the specimen. It was observed that with an increase in gas pressure the cleat spacing also increased. Change in cleat spacing was larger in middle of the specimen as compared to that of the upper and lower ends. Some more fractures were also observed with the increase in gas pressure (Fig. 15). The development of fractures is due to swelling of coal matrix with an increase in pore and gas pressure. At smaller hydrostatic pressure, swelling rate increases positively with stronger expansion effects. However, with increased hydrostatic pressure, the specimen would remain in the compression state, even under sufficient gas adsorption. This leads to expansion of pores and fractures in coal. Internal swelling stress leads to the closure of micro-cleats, but at the same time, the mineral phase had no such internal swelling stress and is less compressible; thus, the open cleats were protected from closure by the mineral phase. The nearby micro-cleats and the pore volume of specimen decreased significantly when the specimen was saturated. A similar behaviour, i.e. strain from 0.51 to 0.55% normal to bedding plane (z-direction) and 0.4–0.48% parallel to bedding plane (x and y directions) were reported elsewhere (Liu et al. 2014).

Fig. 15

Change in cleat spacing with gas pressure

The cleat dimension was correlated with the permeability of coal matrix. Increased permeability from 0.12 to 0.35 mD was observed with the increase in fracture size from 1.01 to 1.98 mm (Fig. 16). As the cleat network is the pathway of gas transportation in coal matrix, the increment in cleat numbers facilitates migration of gas and enhances permeability. The correlation of volumetric change with permeability indicates a reduction in permeability with volumetric changes. Permeability reduced from 0.16 to 0.35 mD with an increase in volume from 0.24 to 2.76% (Fig. 16). Reduction in permeability attributed to the effect of coal swelling and closure of micro-cleats. This compares favourably to similar observation reported elsewhere (Jasinge et al. 2012).

Fig. 16

Change in cleat spacing with pressure

CBM production

The experimental values of coal parameters as well as those from the reservoir were used to predict the CBM production on a 5-year period. A dedicated code GEM (CMG, Canada) was used for the gas production. It works on the concept of Darcy’s law.

The coal sample JH-MD-S₁ at 580 m depth of occurrence and 15.66 MPa initial overburden pressure as well as 0.3031 mD maximum fracture permeability were considered for the determination of production rate (m³/day) and cumulative gas in place (m³) over a 5-year period.

Two-dimensional reservoir model with production wells and horizontal fracturing is represented in Fig. 17. The contour shows the rate of gas production and cumulative gas volume with time. Total gas in place (sum over layer) over 5 years of time has been predicted. The continuous dewatering resulted in decreased bottom hole pressure and migration of gas from coal matrix to cleat structure and finally to well-bore area. The actual surface production varies from 1100 to 1500 m³/day for well 1 to well 4, respectively (Fig. 18). It is observed that the production rate increases continuously to rise beyond 5 years. Actual surface cumulative gas over 5 years of time is projected to vary from 150 to 540 Mm³.

Fig. 17

Total gas in place (sum over layer)

Fig. 18

Production history of production well

Conclusion

The following conclusion is drawn from the mine under investigation at Jharia coal field (Moonidih area).

• Coal of study area belongs to medium-volatile-bituminous (mvb) rank

• Unconfined compressive strength, elastic modulus and Poisson’s ratio of coal samples varied from 2.20 to 7 MPa, 0.42–1.1 GPa and 0.35–0.38, respectively, at the depth ranged from 400 to 580 m.

• Permeability of coal sample varied from 0.377 to 0.97 mD at 6, 10 and 3.5 MPa horizontal, vertical and gas pressures, respectively, for the coal sample from 400 to 580 m depth. The permeability was observed decreasing with depth of occurrence. Decreased permeability with gas pressure and horizontal pressure confirms the closure of pores as well as cleat structure.

• Percentage of reduction in permeability was observed from 22.97 to 24.65 for the coal samples from 400 to 580 m depth of occurrence. Reduction in permeability was observed higher for the coal sample with lower elastic modulus at same level of stress conditions.

• Swelling in coal samples was observed with injection of gas at 4.2 MPa pressure. The swelling leads to expansion of fractures and increment of fracture permeability in coal sample.

• Injection of gas in coal sample from 0 to 4.2 MPa pressure increased the average fracture width from 1.01 to 1.98 mm, and percentage change in volume was observed from 0.24 to 2.76%, respectively. The increase in volume confirms the swelling of coal sample. The coal swelling not only increases the fracture width of the macro-cleats but also closes the nearby micro-cleats of the coal matrix and hence reduces the matrix permeability.

• Surface production rate of all production wells in JH-MD-S₁ coal seam varied from 1100 to 1500 m³/day

• Surface cumulative production ranged from 150 to 540 Mm³