Abstract
Modern downhole temperature measurements indicate that bottomhole fluid temperature can be significantly higher or lower than the original reservoir temperature, especially in reservoirs where high-pressure drawdown is expected during production. This recent finding contradicts the isothermal assumption originally made for routine calculations. In a high-pressure drawdown environment, the Joule–Thomson (J–T) phenomenon plays an important role in fluid temperature alteration in the reservoir. This paper presents a robust analytical model to estimate the flowing-fluid temperature distribution in a reservoir that accounts for the J–T heating or cooling effect. All significant heat transfer mechanisms for fluid flow in the reservoir, including heat transfer due to convection, J–T phenomenon, and heat transfer from overburden and under-burden formations, are incorporated in this study. The proposed model successfully validates the results of a rigorous numerical model that intrinsically honored field data.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Most reservoir engineering calculations presuppose that the fluid temperature entering the wellbore has the same temperature as that in the reservoir, regardless of pressure drop and elapsed time. While the assumption of constant fluid temperature may be true for high-permeability systems, reservoirs undergoing production from low-permeability systems at significant drawdowns may not conform to this simplified assumption. This reality has prompted several studies to probe a radial distribution of the fluid temperature in time.
Early attempts to establish fluid temperature were mainly for heavy-oil reservoir management in thermal recovery operations. One of the earliest models for estimating temperature distribution during steam injection was presented by Lauwerier (1955). Subsequently, several models were presented by Spillette (1965) and Satman et al. (1979) using different approaches. More recently, Tan et al. (2012) compared some of these solutions and offered a solution of their own. All of these models treated heat conduction and convection as main heat transfer mechanisms in the reservoir; however, fluid temperature change due to the Joule–Thomson (J–T) effect remained unaccounted for a given low intrinsic flow rate in heavy-oil reservoirs.
The J–T heating or cooling effect originated from interpreting temperature logs. Steffensen and Smith (1973) proposed an analytical solution for estimating the fluid’s static and flowing temperature at bottomhole during steady-state flow by incorporating the J–T effect. They pointed out that the main heat transfer mechanisms of fluids in the reservoir during production and injection are heat convection and J–T heating (or cooling). Temperature change due to radial conduction is normally negligible. They also proposed that heat transfer between reservoir and overburden and under-burden formations during steady-state flow is negligible; therefore, the “heat transfer to overburden” term was not included in their study. Kabir et al. (2012), among others, showed how independent estimation of individual layer contributions may be made from temperature profiles in both gas and oil wells, with the J–T effect playing a major role. More recently, Onur and Palabiyik (2015) offered an analytical solution for single-phase water flowing in a geothermal reservoir that accounted for the effect of skin. Their approach was to study the use of temperature data for estimating reservoir parameters by history matching. Onur and Cinar (2016) presented an analytical solution accounting for the J–T effect, but not heat exchange with the overburden and under-burden formations.
High-pressure drawdown is normally required to commercially produce from challenging reservoirs, such as those in deep, low-permeability, and overpressure systems. As a result, the impact of the J–T effect on flowing-fluid temperature is more prominent in some of the deepwater reservoirs in Gulf of Mexico. In some cases, the J–T effect may trigger fluid temperature increase of 20–30 °F higher than the fluid temperature at the initial-reservoir condition.
Yoshioka et al. (2005, 2006) introduced a coupled reservoir-and-wellbore analytical temperature model for horizontal well production in a single-phase reservoir, assuming steady-state conditions. An extended version of Yoshioka et al.’s work was presented by Dawkrajai et al. (2006). They developed a finite-difference solution for the coupled reservoir/wellbore system to estimate fluid temperature distribution in the reservoir for two-phase production in horizontal wells. Their numerical solution removes the steady-state assumption and allows variation of reservoir and fluid properties in space and time.
Duru and Horne (2010) developed a semianalytical solution for the same problem, taking into account J–T heating or cooling, as well as heat conduction and convection. They applied the operator-splitting and time-stepping (OSATS) semianalytical technique to solve the problem and split the reservoir energy-balance equation into two parts: convective transport and diffusion. They solved the convective transport part analytically and used the solution to approach the diffusion part. The diffusion part of the energy-balance equation was solved semianalytically; that is, the result from the first timestep is the initial condition for next timestep, and so on. They also coupled the reservoir temperature model with Izgec et al.’s (2007) analytical wellbore temperature model for fluid temperature analysis in the entire production system.
App (2009, 2010) developed a nonisothermal reservoir simulator for single-phase oil flow by coupling mass and energy-balance equations with Darcy’s law. He included all possible heat transfer mechanisms in the reservoir as part of the comprehensive energy-balance equation. While earlier work by other authors in this area generally assumes no heat transfer from a reservoir to its surroundings (adiabatic process), App’s work incorporates potential heat transfer from reservoir to overburden and under-burden formations. His model shows that heat loss to overburden strata is significant and becomes crucial when fluid is significantly heated up later in the production period. He also discussed potential change in well productivity due to J–T heating (or cooling) in high-pressure, high-drawdown reservoirs because fluid viscosity variation depends on temperature change. Ramazanov et al. (2013) proposed a similar numerical model that included convection, radial heat conduction, and the J–T effect. Their numerical model validated their earlier (2007) study and pointed out that the impact of radial conduction to fluid temperature distribution in a reservoir is minimal when the production rate remains constant.
Recently, App and Yoshioka (2013) offered an analytical solution for steady-state fluid temperature change as a function of producing rate, reservoir permeability, and drawdown, among other variables. They used Peclet number (P e = ur/α) to combine production rate and formation thermal conductivity to emphasize the effect of P e on fluid temperature change. They also pointed out that the effect of permeability is included through P e as it incorporates fluid velocity. Their study clearly shows that at high reservoir thermal conductivity when P e < 1, the fluid temperature change is strongly influenced by P e due to rapid conduction of heat through the formation. However, for P e > 3, the influence of P e on steady-state fluid temperature is negligible. The study also shows that fluid temperature changes minimally at very low P e (< 0.1), which appears quite reasonable.
This paper presents an analytical transient-temperature model for estimating the flowing-fluid temperature distribution in a single-phase oil reservoir with constant rate production. The paper also presents an application of this approach to single-phase gas reservoirs. The J–T effect is included as one of the main energy transformation mechanisms of fluid flow in the reservoir. Additionally, heat transfer from a reservoir to overburden and under-burden formations is incorporated in this model formulation following App’s approach. The model is validated with results from the rigorous numerical model developed earlier by App (2010), based on one set of actual field data. Model validation shows that the estimated temperature values compare favorably with those obtained from the numerical simulator.
Model development
Reservoir system
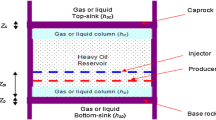
The reservoir system considered in this study is a 1D radial reservoir where fluid flow occurs only in the radial direction. The only flowing fluid in the reservoir is oil, and there is no free gas in the system. Connate water remains immobile. Figure 1 shows a schematic of the reservoir system used in the study. We note that fluid flow in the idealized circular reservoir occurs in the “negative” r-direction. Figure 1 displays this simplified wellbore and reservoir configuration.
Comprehensive energy-balance equation
A principle for estimation of fluid temperature distribution in the reservoir is conservation of energy in the system, which includes reservoir fluid and rock. Conservation of mass for reservoir fluids is also incorporated to achieve a comprehensive energy-balance equation of the system. We also assume that reservoir is perfectly horizontal; thus, gravitational effect (change in fluid potential energy) is negligible.
The general form of thermal energy balance in terms of equation of change for internal energy (Bird et al. 2006) can be written as:
where \(\hat{U}\) is fluid internal energy, ρ is fluid and/or rock density, and \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}\) is fluid local velocity. The ∇· term generally represents the net input rate of energy per unit volume of the system. The first term on the left side of Eq. (1) represents the total rate of internal energy increase in the system. The first and second terms on the right side are net input rate of internal energy to the system caused by convective transport and heat conduction, respectively. The third term represents the net reversible rate of internal energy increase due to fluid compression (pressure difference), while the fourth term is the net irreversible rate of internal energy increase caused by fluid viscous dissipation. The fourth term is also referred to as “J–T” in this study.
In addition to heat conduction, convection, and the J–T phenomenon caused by fluid flow in the reservoir, energy transfer from surroundings (overburden and under-burden formations) to the system (reservoir fluids and formation) is considered in this study. Therefore, a term representing the net energy transfer rate between the system and surroundings, \(\dot{Q}\), is added to the energy-balance equation as the last term in Eq. (1).
Using the principles of rock and fluid enthalpy, Fourier’s law of conduction, Newton’s law of cooling, conservation of mass, and Darcy’s law, Eq. (1) is rearranged and rewritten as
Equation (2) is considered a comprehensive energy-balance equation for the system of interest. The first term on the left side of Eq. (2) contains the heat capacity of oil, water, and rock, which collectively represent energy change due to temperature transient. Similarly, the second term represents convective heat transport. The third term is energy change due to J–T effect, and the fourth term represents energy change due to pressure transient in the reservoir. This pressure transient term is neglected in deriving the analytical solution presented below. The first term on right side reflects change in energy arising from radial heat conduction, and the last term represents rate of heat transfer across system boundary, meaning to overburden and under-burden formations. Details of the comprehensive energy-balance equation are given in “Appendix A.”
Analytical model
We rearranged the comprehensive energy-balance equation of the system by applying all the assumptions described in “Appendix A.” The energy-balance equation can be reduced to a first-order, partial-differential equation (PDE):
The method of characteristics was used to solve the PDE to arrive at a final form of the proposed analytical solution given below. “Appendix B” presents the details of this derivation.
where
and
Equation (4) can be used directly with any software that requires fluid bottomhole temperature as an input, such as in well pressure/temperature traverse calculations and production logging. When we solve Eq. (3) by assuming fluid property variation to be negligible, greater accuracy in estimated sandface temperature can be achieved when radial segments in the reservoir facilitate variation of fluid properties from one node to the next. For temperature computation with Eq. (4), we allowed such variation of fluid properties with pressure and temperature using 100 radial segments with logarithmic spacing in the reservoir. Calculation initiates with known pressure, temperature, and fluid property values at the reservoir boundary. Analytical expressions then facilitate estimation of pressure and temperature at the next node. During these computations, property values are retained from the prior node. New pressure and temperature then allow computation of new property values. This procedure repeats itself until the wellbore is reached. Because pressure, temperature, and viscosity change much faster as the wellbore is approached, logarithmic grid spacing—with a shorter spatial step at wellbore’s proximity—works very well. We have investigated the effect of a number of spatial nodes on computational accuracy and found 100 nodes to be quite satisfactory.
Model validation
App’s (2010) simulated results, which were anchored in field data, formed the cornerstone for model validation. This approach also implicitly verifies the results of the proposed analytical model with those of rigorous numerical solutions offered by App. “Appendix C” presents the reservoir and heat transfer parameters used in these calculations. In all cases, solid lines represent the reservoir temperature profiles estimated with the proposed analytical model. In all subsequent discussions, reference to estimates using the analytical model implies the use of Eq. (4), with the parameters estimated with Eq. (5) through Eq. (10), thereby allowing all fluid properties to vary with pressure and temperature.
In this example, the flowing-fluid temperature distribution in the reservoir is calculated for five different constant production rates: 970, 2050, 3270, 4650, and 6200 STB/D. Figure 2 presents a comparison of solution generated with Eq. (4) with those of App. The solid lines represent the solutions of the analytical model, and the dashed lines do the same for those of App. Each profile represents distribution of the flowing-fluid temperature in the reservoir at different production rates, after 50 days of continuous production at a constant rate. One observes that the temperatures estimated with the proposed model are very close to App’s rigorous, numerical solutions.
Temperature estimations of analytical model at different rates compare favorably with those of App’s (2010) numerical model for 50 days of production
Figure 3 compares the analytical solutions for the sandface oil temperature (solid lines) with those of App (dashed lines). This figure reveals the evolution of flowing-fluid temperature at the sandface with time for the same constant rate production scenarios as before. This figure instills confidence in that the simplified analytical model yields very reasonable estimations of the bottomhole temperature for different production rate scenarios.
Results of the analytical model compare well with App’s numerical model (2010) for the sandface oil temperature
Figure 3 shows that for any constant production rate, the oil temperature rises rapidly with time and then flattens out. Indeed, for high production rates, oil temperature actually begins a slow decline with time after attaining the maximum value. Figure 4 presents this phenomenon in a different way. Each profile of different color represents the flowing-fluid temperature distribution in the reservoir at a particular producing time for a production rate of 6200 STB/D. The solid lines represent our analytical solution, and the dashed lines are from App’s study. Again, we observe that results from the analytical model are very close to the results obtained from App’s numerical simulations. Differences in temperature profiles between the analytical model and App’s simulator are expected because of the significantly more assumptions made to arrive at the analytical solution.
Analytical model agrees well with App’s (2010) numerical model results at different times for the 6200 STB/D producing rate
Examination of Fig. 4 offers several insights. We observe that oil temperature in most of the formation remains unaffected; temperature increase is only noticeable up to about 100 ft from the wellbore for long producing times. The explanation of this phenomenon is simple; most of the pressure drop—the cause for temperature rise—occurs near the wellbore, especially for shorter production periods. In addition, because heat is generated continuously due to J–T effect, longer production leads to greater temperature rise. However, the rate of temperature increase slows down with time, and finally the reversal occurs. Therefore, fluid temperature rise for 400 days (black lines) of production is less than that for 100 days (blue lines). This reversal is captured in both App’s numerical and our analytical solutions.
Let us discuss the two reasons related to reduction and ultimate reversal in temperature rise with time. The primary reason is that our model accounts for fluid heat loss to the overburden and under-burden formations. This heat loss increases with increased fluid temperature. Figure 5 shows the estimated fluid temperature using the rigorous model (solid lines) compared to that estimated assuming no heat loss (everything else remaining the same) to the formation (dashed lines). Note that the maximum temperature after 400 days of flow period is about 10 °F higher when heat loss to the formation is not accounted for compared to when it is. Further analyses of ignoring fluid heat loss to the formation are discussed later.
The other reason for reduced temperature rise with producing time is that oil viscosity depends on temperature and pressure. We have used viscosity data from laboratory measurements for this particular reservoir fluid as presented by App (2010) and is reproduced in Fig. 8 in “Appendix C.” Viscosity, in turn, influences flowing pressure gradient, and consequently, the reservoir pressure. However, fluid temperature depends on heat generation due to fluid expansion, which depends on the pressure gradient, dp/dr. Figure 4 shows this complex interdependency of fluid viscosity, pressure, and temperature in temperature trends.
With the increase in production time, increasing fluid temperature causes lowering of oil viscosity. For a constant flow rate, lower viscosity causes lower pressure drawdown, resulting in higher reservoir pressure than if viscosity had remained constant. Higher pressure, however, triggers increase in oil viscosity, which contributes to increased pressure gradient near the wellbore. This increased pressure gradient in both the analytical and numerical models causes the fluid temperature (black solid and dashed lines in Fig. 4) to be lower than that after 100 days of production (blue lines) after 400 days of production. To investigate the effect of viscosity variation with temperature, we regenerated the solutions with constant fluid viscosity by keeping all other input parameters the same as that for the rigorous model. Figure 6 presents those results with solid lines representing rigorous solution (with property variation), while the dashed lines are for constant viscosity condition.
Lower temperatures in Fig. 6 for lower producing rates represent those with constant viscosity. However, for higher producing rates, the constant viscosity model generally estimates higher temperatures than does the rigorous (variable viscosity) model. Even for higher producing rates though, the trend reverses with producing times. Again, the interdependence of pressure, temperature, and viscosity precipitate these complex temperature profiles. Given the significant discrepancy in temperature profiles exhibited in Fig. 6, we use the temperature-dependent viscosity as default.
In modeling temperature distribution in the reservoir, many investigators have neglected heat transfer to/from overburden and under-burden formations \(\dot{Q}\). This assumption simplifies the modeling approach and results in a much simpler expression for the fluid temperature as a function of radial distance and time; “Appendix B” presents this development. In addition, as Fig. 3 shows, neglecting formation heat loss does not appear to cause significant errors at low drawdowns. However, for higher flow rates and later times, the estimation error can be quite large; Chevarunotai (2014) presents further discussion on this topic.
Model’s application in gas reservoirs
In arriving at the analytical solution for the fluid temperature for fluid flow from the reservoir bulk toward the wellbore, we assumed the fluid to be only slightly compressible, thereby allowing the PDE [Eq. (3)] to be linear. For gas, this assumption of small compressibility is generally untrue. However, by dividing the reservoir into many radial segments with logarithmic spacing, thereby keeping the small spatial steps, the gas compressibility may be still kept small so that Eq. (4) may be applied to a gas reservoir as well. Using this approach, we estimated the sandface gas temperature as a function of producing time and that is shown in Fig. 7. The input values, provided in “Appendix E,” were taken from App’s (2009) study. Good agreement of our estimates with those of App’s numerical solution is evident in Fig. 7.
Discussion
The analytical reservoir temperature solution derived for the simplified reservoir system was validated with App’s numerical model. Although we made several assumptions in our study to simplify the problem to 1D radial reservoir system, the flowing-fluid temperatures estimated by the proposed analytical solutions are very comparable to those calculated by App’s rigorous numerical solution, as shown in all case studies. The simple form of the analytical solutions allows anyone to adopt and apply it to the problems of interest. The proposed solution can also be applied to more complex problems, such as in reservoirs of other geometry by considering the Dietz (1965) shape factor.
The impact of Joule–Thomson phenomenon is actually a function of pressure drop across the reservoir, fluid flow rate, and the J–T throttling coefficient. In general, the J–T coefficient is positive in low-pressure gas reservoir and is negative in high-pressure gas reservoirs and oil reservoirs of any pressure range. As a result, J–T heating becomes the norm in low-to-high-pressure oil and high-pressure (> 7000 psi) gas reservoirs, whereas J–T cooling occurs in low-pressure (< 5000 psi) gas reservoirs. The approach to estimate the flowing-fluid temperature presented in this paper can be used as a basis and adapted for reservoir temperature estimation in gas reservoirs.
Based on model results, we surmise that fluid temperature in the near-wellbore region can be significantly different from the original reservoir temperature. An accurate estimation of the reservoir fluid temperature from the analytical formulations can yield a better estimation of well productivity, which is useful in production optimization and well development planning. A reasonable estimation of the bottomhole flowing-fluid temperature is also advantageous in well design from the standpoints of equipment selection and management of annular-pressure buildup or APB (Oudeman and Kerem 2006; Hasan et al. 2010). When J–T heating is pronounced, excessive heating of annular fluid may result, thereby triggering APB.
The proposed analytical solution also improves wellbore fluid and heat flow modeling because of more realistic temperature evaluation at sandface. The bottomhole flowing-fluid temperature derived from the analytical model can be coupled with wellbore heat transfer model to allow prediction of flowing-fluid temperature along the wellbore. Accurate flowing-fluid temperature profile along the wellbore is also desirable for well design and production optimization, as well as for pressure transient analysis (Onur and Cinar 2016). An accurate estimation of the reservoir fluid temperature from the analytical formulations can yield a better estimation of well productivity index, which is useful in production optimization and well development planning.
To arrive at the analytical solution, we omitted radial heat conduction, meaning the influence of Peclet number on fluid temperature change has been ignored. In “Appendix C,” we show that for the reservoir and fluid properties used in this study, Peclet numbers for all flow rates are higher than 5.6. As App and Yoshioka (2013) showed, the influence of Peclet number on fluid temperature is negligible when it exceeds 3. They also noted that because formation permeability affects oil production rate, it can influence oil temperature increase due to expansion. Earlier, Shook (2001) also reached a similar conclusion in that thermal conduction can be neglected in nonfractured geothermal systems because P e > 1 is satisfied. For the range of cases that we investigated, P e is greater than 5.6, and the effect of permeability, as well as thermal conductivity, is negligible within engineering accuracy. We note that any significant change in the wellbore flowing-fluid temperature is likely to occur in overpressure reservoirs for sustaining high-flow rates, and, in turn, high P e . This reality increases the likelihood of application of the proposed analytical model.
These model results show that fluid temperature in the near-wellbore region can be significantly different from the original reservoir temperature during production. A reasonable estimation of the bottomhole flowing-fluid temperature assists in well design from the standpoints of equipment selection and management of annular-pressure buildup or APB.
Conclusions
This paper presents an analytical model for the flowing-fluid temperature estimation in a single-phase oil reservoir. Concepts of energy balance and conservation of mass were applied to arrive at an analytical formulation to evaluate fluid temperature in a reservoir producing at a constant rate. Fluid temperature change due to the Joule–Thomson effect, as well as energy exchange between a reservoir and its surroundings (overburden and under-burden formations), was incorporated in this study. Results from a rigorous numerical model validated the simplified analytical model within engineering accuracy. Therefore, we reached the following conclusions:
-
1.
The proposed analytical model provides comparable reservoir temperature estimation to the rigorous numerical simulator developed by App (2010), which is anchored in actual field data. Calculations of Peclet numbers suggested that ignoring conductive heat transport appears reasonable for field production rates of interest within the scope of this investigation. Generally speaking, an analytical model is relatively simpler and allows the calculations to be performed in a spreadsheet.
-
2.
The advantage of this analytical model over other analytical solutions for reservoir temperature estimation is that heat transfer from/to overburden and under-burden formations \(\dot{Q}\) is included. While the derivation of the analytical solution neglects property variation, the use of the solution allows for property changes with pressure and temperature. We have shown that \(\dot{Q}\) is crucial in the estimation of flowing-fluid temperature in a reservoir, especially at long producing times when the reservoir fluid is heated significantly, and the reservoir fluid temperature is very different from that in its surroundings.
-
3.
Accounting for viscosity variation with temperature and pressure enhances the accuracy of temperature estimation.
-
4.
The analytical model can be further extended to gas reservoirs by accounting for changing properties, such as density, viscosity, and the J–T coefficient with pressure and temperature.
Abbreviations
- A :
-
Flow area, ft2, L2
- B o :
-
Oil formation volume factor, bbl/STB
- c p :
-
System specific heat capacity, Btu/lbm °F, L2/t2T
- c pf :
-
Formation specific heat capacity, Btu/lbm °F, L2/t2T
- c po :
-
Oil specific heat capacity, Btu/lbm °F, L2/t2T
- c pw :
-
Water specific heat capacity, Btu/lbm °F, L2/t2T
- C J :
-
Joule–Thomson coefficient, °F/psi, TLt2/m
- h :
-
Formation thickness, ft, L
- h c :
-
Heat transfer coefficient, Btu/hr ft2 °F, m/t3/T
- \(\hat{H}\) :
-
Enthalpy, lbm ft2/hr2, mL2/t2
- k :
-
Reservoir permeability, md, L2
- p :
-
Pressure, psi, m/Lt2
- p b :
-
Bubble point pressure, psi, m/Lt2
- p e :
-
Pressure at reservoir external boundary, psi, m/Lt2
- p i :
-
Initial reservoir pressure, psi, m/Lt2
- p wf :
-
Flowing-fluid pressure at well bottom, psi, m/Lt2
- P e :
-
Peclet number (= ur/α), dimensionless
- q :
-
Volumetric flow rate, ft3/hr, L3/t
- \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q}\) :
-
Conductive heat transport, Btu/hr ft2, m/Lt3
- \(\dot{Q}\) :
-
Net heat transfer rate between the system and surroundings, Btu/hr ft2, m/Lt3
- r :
-
Radius, ft, L
- r e :
-
External reservoir radius, ft, L
- r w :
-
Wellbore radius, ft, L
- S :
-
Saturation
- S o :
-
Oil saturation
- S w :
-
Water saturation
- t :
-
Time, hr, t
- T :
-
Fluid temperature, °F, T
- T e :
-
Fluid temperature at reservoir external boundary, °F, T
- T i :
-
Initial reservoir temperature, °F, T
- T s :
-
Temperature of overburden and under-burden formations, °F, T
- T wf :
-
Flowing-fluid temperature at well bottom, °F, T
- \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u}\) :
-
Superficial velocity, ft/hr, L/t
- u r :
-
Fluid local velocity in radial direction, ft/hr, L/t
- \(\hat{U}\) :
-
Fluid internal energy, lbm ft2/hr2, mL2/t2
- \(\hat{V}\) :
-
Specific volume, ft3/lbm, L3/m
- λ :
-
Reservoir thermal conductivity, Btu/hr ft °F, TLt2/m
- α :
-
Thermal diffusivity (= λ/ρc p ), ft2/hr, L2/t
- μ :
-
Fluid viscosity, cp, m/Lt
- ρ :
-
Density, lbm/ft3, m/L3
- ρ o :
-
Oil density, lbm/ft3, m/L3
- ρ w :
-
Water density, lbm/ft3, m/L3
- ρ f :
-
Formation density, lbm/ft3, m/L3
- σ o :
-
Joule–Thomson throttling coefficient of oil, Btu/lbm psi, L3/m
- σ w :
-
Joule–Thomson throttling coefficient of water, Btu/lbm psi, L3/m
- \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau }\) :
-
Stress, lbf/ft2, m/Lt2
- ϕ :
-
Porosity
References
Al-Hadhrami AK, Elliott L, Ingham DB (2003) A new model for viscous dissipation in porous media across a range of permeability values. Transp Porous Media 53(1):117–122. doi:10.1023/A:1023557332542
App JF (2009) Field cases: nonisothermal behavior due to Joule–Thomson and transient fluid expansion/compression effects. In: Paper SPE-124338-MS presented at the 2009 SPE annual technical conference and exhibition, New Orleans, Louisiana, 4–7 Oct 2009. SPE-124338-MS. doi:10.2118/124338-MS
App JF (2010) Nonisothermal and productivity behavior of high-pressure reservoirs. SPE J 15(1):50–63. doi:10.2118/114705-PA
App JF, Yoshioka K (2013) Impact of reservoir permeability on flowing sandface temperatures: dimensionless analysis. SPE J 18(4):685–694. doi:10.2118/146951-PA
Bird RB, Stewart WE, Lightfoot EN (2006) Transport phenomena, 2nd edn. Wiley, New York, p 336. ISBN 978-0470115398
Chevarunotai N (2014) Analytical model for flowing-fluid temperature distribution in single-phase oil reservoir accounting for Joule–Thomson effect. MS Thesis, Petroleum Engineering Department, Texas A&M University, College Station, Texas, USA
Dawkrajai P, Lake LW, Yoshioka K et al (2006) Detection of water or gas entries in horizontal wells from temperature profiles. In: Paper SPE 100050 presented at the 2006 SPE/DOE Symposium on Improved oil Recovery, Tulsa, Oklahoma, 22–26 April 2006. doi:10.2118/100050-MS
Dietz DN (1965) Determination of average reservoir pressure from build-up surveys. J Pet Technol 17(8):955–959. doi:10.2118/1156-PA
Dranchuk PM, Purvis RA, Robinson DB (1973) Computer calculation of natural gas compressibility factors using the Standing and Katz correlation. In: Annual technical meeting, Petroleum Society of Canada, May 8–12, Edmonton, Canada. doi:10.2118/73-112
Duru OO, Horne RN (2010) Modeling reservoir temperature transients and reservoir-parameter estimation constrained to the model. SPE Res Eval Eng 13(6):873–883. doi:10.2118/115791-PA
Hasan R, Izgec B, Kabir CS (2010) Sustaining production by managing annular-pressure buildup. SPE Prod Oper 25(2):195–203. doi:10.2118/120778-PA
Izgec B, Kabir CS, Zhu D et al (2007) Transient fluid and heat flow modeling in coupled wellbore/reservoir systems. SPE Res Eval Eng 10(3):294–301. SPE-102070-PA. doi:10.2118/102070-PA
Kabir CS, Izgec B, Hasan AR et al (2012) Computing flow profiles and total flow rate with temperature surveys in gas wells. J Nat Gas Sci Eng 4:1–7. doi:10.1016/j.jngse.2011.10.004
Lauwerier HA (1955) The transport of heat in an oil layer caused by injection of hot fluid. Appl Sci Res 5(2–3):145–150
Lee AL, Gonzalez MH, Eakin BM (1966) The viscosity of natural gases. Trans AIME 237:997–1000
Onur M, Cinar M (2016) Temperature transient analysis of slightly compressible, single-phase reservoirs. In: Paper SPE-180074-MS presented at the 78th EAGE conference and exhibition, Vienna, Austria, 30 May–2 June 2016. doi:10.2118/180074-MS
Onur M, Palabiyik Y (2015) Nonlinear parameter estimation based on history matching of temperature measurements for single-phase liquid–water geothermal reservoirs. In: Proceedings, world geothermal congress, Melbourne, Australia, 19–25 April 2015. https://pangea.stanford.edu/ERE/db/WGC/papers/WGC/2015/22009.pdf
Oudeman P, Kerem M (2006) Transient behavior of annular pressure build-up in HP/HT wells. SPE Drill Complet 21(4):234–241. doi:10.2118/88735-PA
Ramazanov AS, Nagimov VM, Akhmetov RK (2013) Analytical model of temperature prediction for a given production history. Oil Gas Bus J (1):537–546. http://ogbus.ru/eng/authors/Ramazanov/Ramazanov_4e.pdf
Satman A, Brigham WE, Zolotukhin AB (1979) A new approach for predicting the thermal behavior in porous media during fluid injection. Geotherm Resour Counc Trans 3:621–624
Shook GM (2001) Predicting thermal breakthrough in heterogeneous media from tracer tests. Geothermics 30(6):573–589. doi:10.1016/S0375-6505(01)00015-3
Spillette AG (1965) Heat transfer during hot fluid injection into an oil reservoir. J Can Pet Technol 4(4):213–218. doi:10.2118/65-04-06
Steffensen RJ, Smith RC (1973) The importance of Joule–Thomson heating (or cooling) in temperature log interpretation. In: Paper SPE-4636-MS presented at the SPE-AIME 48th annual fall meeting, Las Vegas, Nevada, 1–3 Oct 1973. doi:10.2118/4636-MS
Tan H, Cheng X, Guo H (2012) Closed solutions for transient heat transport in geological media: new development, comparisons, and validations. Transp Porous Media 93(3):737–752. doi:10.1007/s11242-012-9980-5
Yoshioka K, Zhu D, Hill AD et al (2005) A comprehensive model of temperature behavior in a horizontal well. In: Paper SPE-95656-MS presented at the 2005 SPE annual technical conference and exhibition, Dallas, Texas, 9–12 Oct 2005. doi:10.2118/95656-MS
Yoshioka K, Zhu D, Hill AD et al (2006) Detection of water or gas entries in horizontal wells from temperature profiles. In: Paper SPE-100209-MS presented at the SPE Europec/EAGE annual conference and exhibition, Vienna, Austria, 12–15 June 2006. doi:10.2118/100209-MS
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Comprehensive energy-balance equation of the system
The energy conservation is the underlying principle for the estimation of fluid temperature distribution in the reservoir, involving rock and fluid. Conservation of mass for reservoir fluids allows achieving a comprehensive energy-balance equation of the system. The general form of thermal energy balance, in terms of the equation of change for internal energy, was presented in Eq. (1). This equation can also be written in terms of enthalpy, temperature, and pressure. In other words, Eq. (1) can be rewritten in the following form:
For the 1D radial system, the double-dot product can be represented by Newton’s law of viscosity, \(- \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\tau } :\nabla \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {u} } \right) = 2\mu \left( {\frac{{\partial u_{r} }}{\partial r}} \right)^{2}\), and heat conduction can be represented by \(- \nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {q} = \frac{1}{r}\frac{\partial }{\partial r}\left[ {\lambda r\frac{\partial T}{\partial r}} \right];\) therefore, Eq. (11) can be rewritten as
Al-Hadhrami et al. (2003) examined the viscous dissipation term in the energy-balance equation in Cartesian coordinates. Following their work, we approximated the viscous term for the 1D radial flow in porous media with \(- u_{\text{r}} \frac{\partial p}{\partial r}\). Equation (12) then becomes
Applying mass conservation in 1D radial system, \(\frac{\partial p}{\partial t} + \frac{1}{r}\frac{\partial }{\partial r}(r\rho u_{\text{r}} ) = 0\), Eq. (13) can be rewritten as
Enthalpy of the reservoir rock depends only on its temperature, which is given by dH f = c pfdT. However, the enthalpy of a fluid depends both on its temperature and pressure; that is,
In Eq. (15), c p is the oil specific heat and C J is the Joule–Thomson coefficient. Therefore, reservoir oil enthalpy is expressed by Eq. (16):
where σ o represents the product, − C J c p . A similar expression for the connate water can be written.
We write enthalpy in terms of pressure and temperature for each reservoir component, that is, oil, connate water, and formation rock, and combine all parameters into Eq. (14) to obtain
Equation (17) or Eq. (2) in the text is fundamentally the same as the thermal energy-balance equation presented by App (2009, 2010). This equation is also the basis for our analytical model to evaluate the flowing-fluid temperature distribution in the reservoir.
Let us list the underlying assumptions of this model. This study presupposes that the reservoir is homogeneous, and the rock and fluid properties are time invariant. Other general assumptions include the following:
-
1.
The only flowing fluid in the reservoir is oil.
-
2.
The reservoir is producing at a constant rate.
-
3.
The original temperature of overburden and under-burden formations is the same as the reservoir temperature at initial conditions. The elevation differences from reservoir depth are negligible.
-
4.
Overburden and under-burden formations are infinite sources/sinks. Overburden and under-burden formations remain at their original temperatures even after heat transfer to/from the reservoir occurs.
-
5.
Radial heat conduction is negligible during constant rate production.
-
6.
The pressure transient term, ∂p/∂t, is assumed to be negligible. Therefore, for a given flow rate, pressure varies in the radial direction, but not with time.
-
7.
Fluid temperature and pressure remain constant at the reservoir boundary.
-
8.
Porosity and permeability remains unchanged.
-
9.
Variation in fluid properties of density and viscosity is negligible.
-
10.
The fluid’s local velocity (superficial velocity) can be estimated from Darcy’s equation:
Note that these assumptions are necessary to obtain a useful analytical solution to the flow problem at hand; the model validation section explores the effects of some simplifying assumptions on solution quality.
Appendix B: Analytical solution for reservoir flowing-fluid temperature estimation
A comprehensive energy-balance equation for the system with a consideration of heat transfer between the system and surroundings is given by Eq. (18). Based on our general assumptions, radial heat conduction during constant rate production is negligible. Additionally, ∂p/∂t term is assumed to be minimal and can be omitted. Therefore, Eq. (17) becomes
We rewrite velocity ur in terms of flow rate as q/(2πrh) and rewrite the ∂p/∂r in terms of flow rate as -(μq)/(2πrhk). Also, we replace q with –q because flow occurs in the negative r-direction during production. Therefore, Eq. (20) becomes
The net input rate of energy between reservoir and under- and overburden formations \(\dot{Q}\) is related to the formation undisturbed temperature in a complex manner. We approximate this term by following App’s (2010) approach using Newton’s law of cooling, giving \(\dot{Q} = - 2h_{\text{c}} \left[ {T - T_{s} } \right] /h\), where h c is the heat transfer coefficient. The complete energy-balance equation of the system then becomes
If we use lumped parameters A, B, and C, Eq. (21) can be simplified to the following expression:
Equation (14) is a first-order, partial-differential equation where fluid temperature T is a function of radial distance r from wellbore into the reservoir and producing time t. Initially, fluid temperature in the reservoir is constant at T i. We apply the method of characteristics with the initial condition, \(T\left( {r,t = 0} \right) = T_{\text{i}}\) to arrive at the following solution to Eq. (23):
where
Note that parameters A through H are constant for a particular reservoir and are reported in the main text as Eqs. (5)–(10); Chevarunotai (2014) presents further details of this derivation.
Appendix C: Input data for model validation
We used a real field example, reported previously in App’s study (2010). App had generated his solutions with a newly developed numerical model. Table 1 shows static (rock) properties of the reservoir, which is considered as a base case in this study. We assumed that the reservoir is homogeneous and that the model parameters remain constant throughout the production period. Table 2 presents the reservoir fluid properties. Oil is the flowing phase, and the formation water is considered immobile and that no production of free gas occurs in the reservoir, given the low-saturation pressure.
Another critical fluid property in flowing-fluid temperature and well productivity calculation is oil viscosity. Data from laboratory measurements for this particular reservoir were also presented in App’s paper. Figure 8 presents the oil viscosity as a function of pressure and temperature, which is used for model validation.
Oil viscosity as a function of pressure and temperature (after App 2010)
An important assumption in our model is that conductive heat flow for our problem is negligible. App and Yoshioka (2013) has shown that the effect of formation thermal conductivity can be represented by the Peclet number. Relating fluid velocity u to production rate q, App and Yoshikawa expressed P e as follows:
Their work showed that when 0.1 > P e > 3, the effect of Pe, and, therefore, formation thermal conductivity λ on fluid temperature change due to expansion, is negligible. The calculations for P e for our lowest production rate of 970 STB/D are
Similarly, for our highest production rate of 6200 STB/D, P e = 36.3. Therefore, for the cases considered in this study, omitting thermal conductivity of the formation does not introduce any significant error. We note that for most deepwater assets, economic production rates are expected to be high enough to result in correspondingly high Peclet numbers. As a consequence, the underlying assumptions made while deriving the analytical formulation of this coupled fluid and heat flow problem appear reasonable.
Appendix D: Gas properties
To make our model suitable for gas temperature calculation, we allowed several properties to vary. The models or correlations used for these computations are presented below.
Gas viscosity
Gas viscosity correlations have been presented by a number of authors. For our calculations, we used the one by Lee et al. (1966):
where
Gas density
The gas density is calculated from real gas law, as follows:
where ρ is gas density in gm/cc, M a is apparent molecular weight, T is the temperature in °R, Z is the gas law deviation factor, and p is the pressure in psia.
Joule–Thomson coefficient
An expression for calculating Joule–Thomson coefficient for real gases has been developed by Hasan et al. (2010):
Equation (40) requires accurate estimates of Z and \(\left( {\frac{\partial Z}{\partial T}} \right)_{p}\). We use the following expression for these by Dranchuk et al. (1973):
In Eq. (41), ρ is a polynomial function of p r (= p/p c) and T r (= T/T c), which is given by
The constants are as follows:
a = 0.06423, b = 0.5353T r − 0.6123, c = 0.3151T r − 1.0467 − 0.5783/T 2 r , d = T r , e = 0.6816/T 2 r , f = 0.6845 g = 0.27p r
The Newton–Raphson approach is used to solve for Z and \(\left( {\frac{\partial Z}{\partial T}} \right)_{p}\).
Appendix E: Properties for low-pressure gas DST
The following properties are taken from App (2009) for temperature analysis of a low-pressure gas production test (Tables 3, 4).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Chevarunotai, N., Hasan, A.R., Kabir, C.S. et al. Transient flowing-fluid temperature modeling in reservoirs with large drawdowns. J Petrol Explor Prod Technol 8, 799–811 (2018). https://doi.org/10.1007/s13202-017-0397-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0397-0