Abstract
Commercialization of the steam-assisted gravity drainage (SAGD) process has made recovery of heavy oil/bitumen possible in a number of reservoirs hindered by hydrocarbon immobility. However, the economics of this process are highly sensitive to the efficiency of steam creation, delivery, and use, with a successful and unsuccessful SAGD well pair often separated by how effectively thermal inefficiencies can be mitigated in the flow profiles of steam injection and/or in emulsion recovery. To improve flow profiles, Albertan SAGD completions have experimented with the addition of flow control devices (FCDs). These completion tools have historically been used to regulate liquid inflow across long producing laterals, adding a variable pressure drop along the lateral to improve the conformance of hydrocarbon production and delay water breakthrough; within SAGD completions, FCDs find novel use to force a more even flow distribution of steam in the injector and a thermally dependent inflow profile in the producer to maximize recovery of heavy oil/bitumen. This paper provides a comprehensive overview of different FCD designs, discussing their respective methods of regulation, the fluid-adaptive behavior of “autonomous” FCDs, operational strengths and weaknesses of different commercial offerings, and suggestions on how to use existing pressure loss models for FCDs and apply them to the non-traditional application of regulating SAGD flow profiles, both for equipment sizing and estimation of pressure loss/flow rates across the device. From this work, it is proposed that use of autonomous FCDs in the production lateral are of greater value than use of flow control in the injector; however maximum benefits are achieved by coupling simple orifice-style FCDs in the injector lateral with autonomous, large flow path (non-orifice) FCDs capable of controlling steam flash events in the production well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Starting in the 1980s, advances in drilling technology have made horizontal and multilateral wells a primary design type to economically develop reservoirs particularly with unconventional resources. Horizontal wells have been widely used to increase wellbore contact with the reservoir, increase flowing area, and thus, increase the well productivity by reducing coning tendencies, mitigating the risk of sand production, connecting disconnected drainage areas, and generally lowering drawdown-related production problems (Babu and Odeh 1989; Joshi 2003; Dikken 1990; Ihara et al. 2013; Novy 1995).
Due to higher drawdown at the heel of a horizontal well, the “heel-to-toe effect” occurs which leads to early breakthrough (Li et al. 2013; Li and Zhu 2010; Moen and Asheim 2008; Sagatun 2010). During “heel to toe effect,” as the in-situ oil vacates the region near the heel more rapidly than at the toe, any existing gas cap or aquifer is seen as advancing more quickly toward the wellbore in this regions than at points along the wellbore with lower flux (Atkinson et al. 2004; Tabatabaei and Ghalambor 2011).
Because flow in the wellbore is interdependent with flow in the reservoir, even when the wellbore pressure drop is insignificant relative to reservoir pressure drop, non-conformance of the injection/production fluid front may still be observed. In these cases, an uneven profile is generated by difference in horizontal and/or vertical permeability distribution (Al-Khelaiwi et al. 2010; Baker et al. 2008; Nasr et al. 2000; Yang and Butler 1992), variations in porosity (Llaguno et al. 2002), water saturation heterogeneity (Baker et al. 2008), variations in the distance between the wellbore(s) and fluid contacts (Al-Khelaiwi et al. 2010; Baker et al. 2008; Edmunds and Chhina 2001), variations in localized reservoir pressure (Al-Khelaiwi et al. 2010; Tabatabaei and Ghalambor 2011), changes in capillary pressure and relative permeability along the wellbore (Wang and Leung 2015), localized skin damage or fractures (Furui et al. 2005; Tam et al. 2013), changes in mineralogy or wettability (Ipek et al. 2008; Le Ravalec et al. 2009; Pooladi-Darvish and Mattar 2002), changes in thermal properties (Bois and Mainguy 2011; Irani and Cokar 2016), changes in fluid density, viscosity, or both (Gates et al. 2008; Larter et al. 2008), and the presence or absence of in-situ emulsifiers that blend reservoir and/or introduced fluids into (Ezeuko et al. 2013). With the exceptional of geospatial heterogeneity, like variations in the distance between wellbore(s) and fluid contacts, these root causes serve to change the local mobility ratio. When the local mobility ratio deviates strongly from the average mobility ratio along the wellbore, thief zone communication, sand production, and/or uneven production/injection profiles will occur (Green and Willhite 1998). This coning behavior undermines the economic value of a horizontal well as the most productive zones are now producing an unwanted fluid (water, gas) while oil reserves are ineffectively recovered from other points along the reservoir.
To control or regulate fluid velocity or fluid flow rate within a horizontal well, flow control devices (FCDs) are implemented (Foster et al. 1987). The larger family of devices accomplish this task in a multitude of roles, inclusive but not limited to subsurface safety valves (SSSVs), wellhead chokes, flow metering valves, valves downstream of the well within the process chain (surface safety valves), and downhole throttles on reservoir flux (Denney 2015; Li et al. 2013). Used in this fashion, downhole FCDs are often referred to in industry as “inflow control devices” or “injection control devices” (ICDs), depending on the direction of reservoir flux (Banerjee and Hascakir 2015; Bybee 2008; Jain et al. 2013).
The first downhole field application of FCDs for the recovery of hydrocarbon is credited to Norsk Hydro and Baker Hughes in the early 1990s (Al-Khelaiwi and Davies 2007; Bybee 2008; Mikkelsen et al. 2005). In this first industrial trial, flow control devices were applied to horizontal wells in the Troll field, a subsea giant gas field found on the Norwegian shelf of the North Sea. The Troll field is characterized by a thin oil column (Halvorsen et al. 2012; Henriksen et al. 2006). The main reservoir drive mechanism of this field is gas expansion so horizontal wells were selected and placed ~ 0.5 meters above the oil–water contact to maximize oil recovery despite initial water cuts typically being higher than 50% (Mikkelsen et al. 2005). Because coning of the gas cap dominated the hydrocarbon production, FCDs were placed to regulate the production profile and longer horizontal laterals were drilled. This way water/gas breakthrough was delayed, longer well life was observed, higher cumulative oil production was obtained, and net present value (NPV) was increased (Henriksen et al. 2006).
Since that initial field trial, FCDs/ICDs have been extensively used across the globe to delay water/gas breakthrough in high production rate horizontal wells (Abdelfattah et al. 2012; Al-Khelaiwi and Davies 2007; Jain et al. 2013; Karim et al. 2010; Li et al. 2013). In late 2008, FCDs were proposed for the use in a steam-assisted gravity drainage (SAGD) well pair. A field trial on Surmont well pair 102-06 was started in late 2009 to assess the validity of these theories with promising results (Stalder 2013; Vachon et al. 2015). However, in this type of FCD design, unlike to other applications of FCD, both heat and mass transfer concepts must be considered together to define fluid flow. Hence, addition to the gas coning control problems encountered in light-oil applications, multiple conformance issues were identified in SAGD horizontal wells (Stalder 2013).
Before discussing these problems, it might be useful to define SAGD process first and then, the problems associated with steam injection and bitumen/water production will be discussed.
Overview of steam-assisted gravity drainage
The two horizontal well configuration used in the SAGD process have typical lateral length ranging from 500 to 1500 meters with laterals arranged parallel to each other in a vertical plane a few meters from the bottom of the pay zone (Butler and Stephens 1981a; Wilson 2015). Interwell spacing vertically is typically 5 meters, though drilling tolerances may cause this distance to vary anywhere between 3 and 10 meters (Irani 2013). These horizontal wells are surrounded by heavy oil/bitumen reserves (HO–B), a low-value product that is economically unrecoverable at native viscosity and temperature (Edmunds and Gittins 1993). The steam chamber development unique to SAGD due to its well configuration makes the bitumen extract feasible.
To initiate a steam chamber, steam is circulated in both wellbores for a period of up to 3 months through tubing and out of the annulus (Chen et al. 2008; Gates and Chakrabarty 2006). Thermal energy moves via conduction between the two wellbores (Irani and Cokar 2016). Once thermal and hydraulic communication between the two wellbores is established, true SAGD begins. The upper well in the pair no longer circulates steam but injects it into the reservoir (Irani and Ghannadi 2013). The bitumen flows at the edge of the steam chamber to the production well (Butler et al. 1981; Butler and Stephens 1981a, b; Butler and Yee 2002; Chow and Butler 1996).
As mobilization of bitumen is dependent on delivering thermal energy via steam, it is unsurprising that the economics of SAGD are controlled by the costs of generating steam and waste water treatment/recycling of the produced condensate (Yang et al. 2009; Morrow et al. 2014;). Additionally, SAGD is often criticized for its environmental footprint; in spite of its viability as a bitumen extraction technique, SAGD generates considerable greenhouse gas (GHG) emissions in the process of generating the quantities of steam necessary for the process (Al-Murayri et al. 2011; Brandt 2012; Kovscek 2012 Welch 2011). Based on field data, between 2 and 5 tons of steam are injected into the reservoir to produce each ton of bitumen (Gates and Leskiw 2010). This illustrates how critical energy maintenance is to the SAGD process, with an optimal process delivering injected energy solely to producible bitumen.
Thus, effective utilization of steam through homogeneous distribution along the horizontal well is very important to minimize the environmental impact of SAGD and maximize the oil production from SAGD.
Steam bypassing from injection to production well is another factor impacts the thermal efficiency of steam injection. The producer is designed to remove condensed steam and movable bitumen through gravity drainage. If the condensation rate of fluids is in balance with the fluid movement created by gravity, then, the steam bypassing is prevented (Yuan and Nugent 2013). During bitumen production, a liquid pool is formed around the production well. This liquid pool, being denser than steam, is not easily displaced by the steam phase and prevents live steam from flowing directly into the producer. This phenomenon is known as steam trap and the maintenance of this liquid pool is called steam trap control (Gates and Leskiw 2010).
In field practice, the liquid level cannot be directly measured from surface. Instead, temperature gauges are installed along the length of the producer well to measure the temperature difference between the fluid exiting the upper injector and entering the lower producer. This temperature difference is referred to as subcool and serves as a surrogate variable for liquid level height (Wilson 2015). The smaller the interwell subcool difference, the closer the produced liquids are to the steam temperature, and thus the smaller the height of the liquid pool (Gotawala and Gates 2012). However, subcool is not constant along the length of the production lateral; there is localized variability in subcool. Moreover, flow capacity of the wellbore is large compared to that of the reservoir in the same direction, making compensating steam movement in the reservoir difficult (Vander Valk and Yang 2007). Furthermore, local liquid levels cannot effectively drain parallel to the well due to the very low drainage angles (Edmunds 2013). Too low an average subcool and steam breakthrough will occur at points along the producing lateral, negatively impacting cumulative steam to oil ratio (cSOR), thermal efficiency, and the economics of the project. Too large an average subcool and liquid occupies a significant fraction of the steam chamber, preventing the free movement of steam to the chamber boundaries and potentially flooding the injector well itself (Banerjee et al. 2013b; Carpenter 2015; Gotawala and Gates 2012). Flow control devices (FCDs) are used to overcome the problems with uneven steam trap height, allowing for more aggressive production rates and less manipulation of subcool.
Types of flow control devices
Multiple differing FCD geometries have been commercialized to accomplish the goal of equalizing reservoir flux along the wellbore. All FCD geometries are similar in that they induce an additional pressure drop as fluid travels between the reservoir and the completion base pipe so that the total pressure drop for any fluid flow path is equivalent and thus fluid conformance is maximized (Atkinson et al. 2004). However, the mechanism by which this pressure drop is created can vary wildly between geometries, resulting in drastically different long-term injection/production behavior as reservoir and operational conditions change (Carpenter 2015; Denney 2015). Following sections will explain the existing FCD types.
Channel-style flow control devices
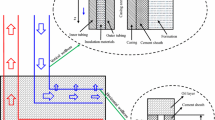
Channel-style flow control devices (FCDs) are one of the earliest geometries of FCDs used downhole in the oil and gas industry (Banerjee et al. 2013b; Li et al. 2013). It is the first type of FCD used to equalize production on a horizontal producer (Al-Khelaiwi and Davies 2007; Henriksen et al. 2006; Mikkelsen et al. 2005) as well as the first geometry used in a SAGD production well (Stalder 2013). Common geometries include helical channels wrapped around a base pipe and labyrinth pathways. Figure 1 is an illustration of a helical geometry on a joint of production pipe. Fluids move from the reservoir through a sand control screen to filter out solid materials. The remaining fluid phase moves in a micro-annulus between the screen and base pipe into the ICD subassembly where it must pass through one or more constant area channels set in parallel. Upon exiting the helical channels, the produced fluid passes through perforations into the production tubing (Qudaihy et al. 2005).

Adapted from Bitto (2005)
Expanded view of flow in a channel-style FCD.
Predicting multiphase flow performance through a channel has been well established in fluid flow mechanics. For fully developed flow in a horizontal pipe, the pressure drop may be expressed as (Lauritzen and Martiniussen 2011; Lee et al. 2013):
In this equation, L [ft] is the length of the channel, D [ft] is the diameter of the channel, v is the fluid average velocity [ft/s], g c [lbm−ft/lbf−s2] is the gravitational constant, and f is the dimensionless friction factor which is the function of Reynolds number (N Re);
In where d h [ft] is the hydraulic diameter, ρ [lbm/ft3] is the density, v [ft/s] is the fluid velocity, µ [cP] is the viscosity, and a 1, a 2, b 1, b 2, c, d, and t are empirically determined dimensionless constants intended to force a fit of the model to experimental data (Lee et al. 2013).
Reynolds number is defined as the ratio of the inertial forces to viscous forces. Viscous forces consist largely of fluid drag along the channel walls while inertial forces refers to shear forces within the fluid that resist changes in direction or velocity (Bird et al. 1960; Lauritzen and Martiniussen 2011). The ratio of the inertial forces to viscous forces creates the pressure drop across pipe and the channel-style FCDs placed in the pipe induce pressure drop over a longer interval which creates an advantageous condition where erosion or plugging of the FCD can be avoided (Al-Khelaiwi and Davies 2007; Visosky et al. 2007). However, this device’s dependence on friction to generate the majority of its pressure drop makes it highly sensitive to the viscosity of the flowing fluid.
Restriction-style flow control devices
For multiple industries, it is a common practice to flow liquid and gas mixtures through restriction-style chokes (Ajienka et al. 1994; Alimonti et al. 2010; Almeida 2013; Campos et al. 2014; Elgibaly and Nashawi 1998; Grose 1985; Kojasoy et al. 1997; Perkins 1993; Schüller et al. 2003; Zhang and Cai 1999). Specifically, within the oil and gas industry, restriction-style FCDs are heavily used as wellhead chokes to control production from wells, as a critical part of single or multiphase flow measurement valves, and within gas lift valves (Ajienka et al. 1994; Al-Attar 2013; Almeida 2013; Surbey et al. 2013). In SAGD operations, restriction-style FCDs have been used in injection wells as a “steam splitter,” a tool to both mechanically divert steam down the wellbore, add additional points of steam injection, and control the rate of injection into particular reservoir zones to equalize steam delivery along the lateral length (Ghesmat and Zhao 2015; Medina 2015).
Figure 2 portrays a restriction-style FCD arranged for production well (Oyeka et al. 2014). Here, an optional sand control screen is illustrated around a production base pipe. Fluid produced from the reservoir is filtered of solid material by the sand control media before being channeled into a micro-annulus between the screen and base pipe. This annular gap is adjusted by wire stand-offs which separate the annulus into several sections evenly distributed around the circumference of the base pipe, providing the dominant flow path (Atkinson et al. 2004). When the fluid reaches the end of the pipe, it encounters the FCD subassembly where it encounters a sudden restriction in its flow path, oriented axially in this illustration. This constriction to flow creates a differential pressure drop across the restriction, in line with Bernoulli’s principle for incompressible flow (Darby 2001; Van Ness and Abbott 2008). Fluid, once downstream of the FCD, encounter perforations to allow entrance into the production base pipe (Banerjee et al. 2013a). If the restriction-style FCD is oriented radially, the FCD also serves as the entrance into the production base pipe (Al-Khelaiwi and Davies 2007). The particular type of restriction may vary with common styles including thin and thick orifice chokes, nozzles, short tubes, and venturi restrictions (Abdelfattah et al. 2012; Atkinson et al. 2004; Banerjee et al. 2013a, b; Banerjee and Hascakir 2015; Bybee 2008).

Adapted from Oyeka et al. (2014)
Expanded view of a restriction-style FCD in a production joint.
Significant effort has gone into characterizing flow behavior across restriction-style chokes by numerous researchers. Published models fall into either empirical or theoretical models (Alsafran and Kelkar 2013; Elgibaly and Nashawi 1998). Empirical models largely follow the form of Gilbert (1954), and include proposed models by Ros (1960), Achong (1961), Ashford and Pierce (1975), and Osman and Dokla (1992). These models were developed on specific ranges of data and should not be used to extrapolate beyond those ranges (Alsafran and Kelkar 2013; Elgibaly and Nashawi 1998).
The second category, theoretical models, attempts to derive performance relationships from mass, momentum, and energy balances. Models within this group are more often used by industry due to their ability to model both critical and subcritical flow, adding to a perception of greater accuracy (Alsafran and Kelkar 2013). Note that the critical flow occurs when fluid velocity across the restriction is equal to the speed of sound in that medium, conversely, subcritical flow is when fluid velocity is less than the speed of sound. If the flow is subcritical, the flow rate is related to the pressure drop across the restriction. However, if the flow is critical, the pressure drop is related only to upstream pressure as reduction in downstream pressure cannot be communicated upstream (Darby 2001; Janssen 1967; Ramamurthi and Nandakumar 1999; Roul and Dash 2012). To optimize a restriction-based FCD, understanding the critical/subcritical boundary and the fluid flow pattern across the restriction is of absolute importance. Prominent theory-based restriction models used by industry include those proposed by Sachdeva and Schmidt (1986), Perkins (1993), Fortunati (1972), and Alsafran and Kelkar (2013) as their models are able to simulate the physical phenomena in both subcritical and critical regimes.
In single-phase fluid flow, the theoretical analysis to evaluate pressure drop caused by abrupt contraction of the flow area is accomplished with one-dimensional analysis. We begin by considering the orifice restriction case: as a fluid stream passes through a sharp edge “thin” orifice restriction, the flow contracts to an area smaller than that of the orifice itself. This smaller area, A c, is called the vena contracta (Van Ness and Abbott 2008). As fluid converges toward the opening of an orifice, it builds up considerable inward radial momentum that causes the flow stream to continue to flow “inwards” for a distance downstream of the restriction (Darby 2001; Sahin and Ceyhan 1996). As the flow stream continues downstream of the vena contracta the flow expands in an irreversible process to the pipe cross-sectional area, A. Correspondingly, the pressure of the flow stream decreases across the restriction and continues to decrease to the point of the vena contracta, with some recovery of pressure occurring as the flow stream expands outward to the pipe cross-sectional area.
As establishing the pressure drop across a restriction-style FCD is not an analytical exercise, optimizing usage for the production lateral in a SAGD completion is difficult. Establishing single-phase flow behavior for emulsions of bitumen and condensate is a daunting enough task, given the variability with phase externality and temperature. To then run multiple laboratory trials with steam to obtain an empirical fit and appropriate two-phase multiplier correction factor borders on impossible when cost and effort are considered. Yet, restriction-style FCDs can be optimized and analytically modeled for the pseudo-multiphase fluid that passes through the injector in SAGD well pairs. High-quality steam is used for injection in SAGD projects, which means that the injected steam behaves as a multiphase mixture of liquid and vapor (Medina 2015). However, this two-phase flow behavior is not as complicated as others (Steven and Hall 2009). Thermal EOR operations use wet steam, a mixture of saturated liquid and saturated vapor, which maintains equilibrium conditions (Chien and Schrodt 1995). The thermodynamic properties of steam are also well known and available in published steam tables (Griston and Cire 1989). The rate of steam injection and steam quality are all controllable factors. As a result, the general orifice flow equation may be adapted for wet steam as follows (Chien and Schrodt 1995):
where w [lbm/hr] is the steam flow rate, σ [dimensionless] is the ratio of restriction diameter to pipe diameter, C d [dimensionless] is the discharge coefficient, d is the restriction diameter [inches], F a [dimensionless] is the thermal expansion coefficient, and Y 2 [dimensionless] is the vapor expansion coefficient. These last two coefficients are calculated according to Miller (1996). The last term, v exp [ft3/lbm] is the two-phase specific volume of the steam as it flows through the restriction. James (1965) offers Eq. 31 as a means of calculation of v exp:
Here, X [percent] is the steam quality, v fg [ft3/lbm] is the specific volume of vaporization, and v f [ft3/lbm] is the specific volume of the saturated liquid. A and B are dimensionless constants that are experimentally determined for a specific range of steam pressure and temperature. Using Eq. 5, inexpensive restriction-style FCDs can be optimized and easily modeled for SAGD injector wells where steam trap control/FCD autonomy is not a necessary feature for establishing fluid conformance.
Autonomous hybrid flow control devices
A fundamental problem that exists with most passive FCDs is how they respond to breakthrough for unwanted fluids. The restriction-style and frictional-style FCDs can improve conformance and delay breakthrough (as might occur due to a fracture, well trajectories that bring segments of the lateral close to gas cap/aquifer, etc.) of unwanted water/gas/steam depending on the goals of their installation. However, these FCD geometries exhibit lower pressure drop for the unwanted fluids than they do for the oleic hydrocarbons. As a result, that segment will see an increase in flow rate and in water/gas cut compared to other segments of the lateral, potentially creating a new non-conforming fluid profile later in well life. The class of FCDs known as “autonomous” FCDs reverses this behavioral trend. Instead of a reduced pressure drop for unwanted fluid, autonomous FCDs increase the pressure drop to unwanted fluid. Hence, if an unwanted breakthrough event happens, the segment in contact with the unwanted fluid exhibits a decrease in flow rate compared to other segments in the lateral, correcting the conformance profile along the lateral over time.
At this point, it is important to distinguish “autonomous” FCDs from “active” FCDs; autonomous FCDs exhibit the control over unwanted fluids passively and without operator intervention relying on properties intrinsic to the fluid or fluid regime to trigger changing behavior. By contrast, active FCDs (such as intelligent control valves and FCDs with sliding sleeves.), require oversight by operators and direct intervention in order for there to be a change in performance behavior. Three commercial FCD geometries exhibit autonomous behavior: fluidic diodes, rate-controlled production valves, and hybrid FCDs. However, the manner by which each provides autonomy varies wildly from manufacturer to manufacturer and introduce new operational advantages and risks depending on the mechanism of action.
The fluidic diode FCD alters how restrictive it is to fluid flow based on the spinning momentum of the fluid passing through (Least et al. 2014). Autonomous behavior is achieved by driving fluid flow through preferential channels based on the fluid’s inherent inertial and viscous forces with simplified internal FCD geometry described in Fig. 3. If viscous forces are dominant, fluid is fairly evenly divided between the straight and divergent pathways of Fig. 3, a typical response for most oils. However, fluids where inertial forces are significantly greater than viscous forces (e.g., gas and water) will favor the straight pathway and bypass the divergent pathway (Fripp et al. 2013). Viscous fluids moving through the divergent pathway are generally lower velocity, and as such require little change in angular momentum to exit the FCD and exhibit minimal rotation in the vortex chamber. If moving through the straight pathway, fluids enter the vortex chamber tangentially and with higher angular momentum. This momentum must be dissipated and fluid velocity reduced by frictional drag while spinning within the vortex chamber before the fluid flow path can be directed to the FCD exit.

Adapted from Fripp et al. (2013)
Simplified Internal Schematic of a Fluidic Diode FCD.
Physically, the fluidic diode occupies a space similar in size to a credit card. Figure 4a is an external view of a fluidic diode device while Fig. 4b illustrates the housing into which the fluidic diode FCD is secured to a production joint. Due to its reduced size, the pathway cross-sectional area is quite small compared to its commercial peers, leading to higher velocities for the same volumetric flowrates and raising questions about potential operational risks with channel plugging or erosion. Similar to frictional-style FCDs, fluidic diodes performance is highly dependent on fluid viscosity. As such, it shares similar issues regarding changing performance as production fluid viscosity changes due to emulsification, temperature change, etc. Unlike frictional-style FCDs, the fluidic diode only provides a pressure drop in one direction, either injection or production, depending on installation. Thus, fluidic diodes will not equalize steam distribution during SAGD start-up and circulation, only production profiles during true SAGD.
Figure 5 provides an illustration of the flow path from the reservoir, through the fluidic diode FCD, and into the base pipe. An additional concern is that should a fluidic diode induce steam flashing, it is most likely to occur at the exit nozzle and thus jet uncontrolled steam into the production tubing.
A second autonomous FCD geometry is that of the Rate-Controlled Production (RCP) valve. This FCD geometry modifies a more traditional restriction-style FCD by introducing a moving disk into the flow path. The position of this disk is dependent on the fluid properties and flow conditions within the RCP. For highly viscous and heavy oils, the disk remains at the bottom of the FCD chamber and provides no obstruction to the restriction at the FCD exit. However for low viscous fluid (e.g., gas), the pressure on the flowing side of the disk is lower than the pressure on the back side of the disk due to the high velocity of the flowing fluid. In this case, the pressure imbalance pushes the disk upward toward the disk seat and reduces the flow area of the exit orifice (Halvorsen et al. 2012). Figure 6a, b illustrates the changing disk position for oil and gas flow while Fig. 6c shows how the RCP valve is inset into the production joint.
Expanded view of RCP insert in base pipe Movement of the RCP internal disk under oil and gas flow conditions (Halvorsen et al. 2016)
When reduction in flow area at the exit orifice occurs, there is a corresponding increases in pressure drop across the FCD. Though the RCP has the strongest autonomous response to unwanted gas flow of any commercial autonomous FCD, it brings with it a number of operational challenges that limit its suitability for field use. One immediate concern is FCD orientation; should the RCP not be installed in the well with gravity initially pulling the internal disk downward, the FCD will not function as designed. Another major concern is in the operational reliability of the disk itself; dependent on a moving part, the FCD fails should the disk ever jam, deform, break, or have its range of motion compromised by foreign materials (Banerjee and Hascakir 2015). In contrast, no other FCD geometry introduces the additional risk of a moving part. Erosion and plugging continue to be an operational risk of the exit orifice, just as it is for the RCP’s non-autonomous counterpart. Finally, the throughput of the RCP is exceptionally low. To quantify this, a flow rate of 2.5 gallon/min [16.37 m3/day] of water across the RCP would require a drawdown on the order of 450 psi [21.55 kPa], well beyond a desirably pressure drop for such a low production flowrate.
The final autonomous design available commercially is the hybrid FCD (Fig. 7), a design that uses multiple restrictions in series placed in a labyrinth pathway. This design hybridizes restriction-style FCDs (by using multiple restrictions within the flow path) and frictional-style FCDs (by creating pressure losses through wall drag and tortuosity) while providing autonomous choking to steam. By distributing the pressure drop over multiple subcomponents, no one individual point of pressure loss is critical to overall function. Cross-sectional flow area through this geometry is 4–10 × larger than other autonomous FCDs, significantly lowering internal velocities and thus, lowering the risk of both plugging and erosion (Banerjee et al. 2013b). The staggered restrictions within this geometry also serve to add a secondary control over steam flashing. Should steam flashing across the restriction of any given cell, the downstream cells serve to create a stronger choke to steam passage, controlling the rate at which it may enter the production tubing. Figure 7 provides a view of the interior of the hybrid FCD along with a close up view of one of the selectable flow paths; depending on which flow path is left unplugged, the pressure drop behavior across the hybrid FCD may be scaled up or down due to the number of cells in the flow path.
Unlike most other FCDs, multiphase testing has been done on the hybrid FCD by third-party laboratories. As a result, this geometry has one of the better characterized pressure drop response to a multiphase fluid. Lee et al. (2013) have suggested that multiphase performance may be accurately described by Eq. 6, where the pressure drop across a hybrid FCD is dependent on a unique friction factor term (ff mixture) that is a function of the dimensionless Reynolds number. This friction factor term is defined in Eq. 7.
Here ff mixture and N Re are dimensionless numbers, l channel is the length of the FCD channel [ft], D h is the hydraulic diameter [inches], ρ mixture is the mixture density [kg/ft3], v mixture is the mixture velocity [ft/s], g c is the gravitational constant [lbm−ft/lbf−s2], and a 1, a 2, b 1, b 2, c, d, and t are dimensionless constants used to fit the empirical laboratory data for multiphase flow.
Like the fluidic diode, the hybrid FCD has no moving parts to introduce additional operational risk. It is less prone to plugging or erosion due to the larger flow areas within its geometry. The redundancy of restrictive cells placed in series provides a theorized benefit in terms of controlling a steam flash event within the FCD. This geometry, unlike the fluidic diode, has demonstrated viscosity insensitivity up to 300 cP. Finally, the hybrid FCD has the most extensive run history for both heavy oil and conventional FCD use.
Summary
There are multiple inflow/injection control device (FCD) geometries commercially available with varied focus on specific operational risks or methods of generating a pressure drop (Fripp and Dykstra 2013; Fripp et al. 2015; Garcia et al. 2009; Loretz and Hosatte 2007; Russell et al. 2013a, b). Yet all FCDs may be sorted into three broad categories: channel-style FCDs, restriction-style FCDs, and autonomous FCDs (Al-Khelaiwi and Davies 2007; Banerjee et al. 2013a; Lauritzen et al. 2011).
While FCD performance has been reasonably well characterized for controlling water breakthrough, no public data exists for FCD performance for fluids at or near saturation temperature as would exist in a SAGD process (Riel et al. 2014; Vachon et al. 2015). Limited information exists for FCD performance with any sort of gas-phase fluid (Coronado et al. 2009; Lauritzen and Martiniussen 2011; Lauritzen et al. 2011; Least et al. 2014, 2013; Lee et al. 2013; Peterson et al. 2010). For a SAGD injector, steam splitters have a limited run history, but not in conjunction with any sort of production control and with little to no performance characterization (Kyanpour and Chen 2013; Medina 2015). Therefore, we summarized strength and weakness of the existing FCDs for SAGD use with two tables. Table 1 summarizes the operational strengths and weakness of all FCD geometry categories for the SAGD application. Table 2 expands upon autonomous FCD subtypes with details again provided in the relevant subsection.
As a result, hybrid autonomous FCD design seems to yield better response than the other FCD designs for SAGD. Detailed public evidence that FCDs provide a benefit to the SAGD process has long been limited to a single field trial, the Surmont 102-06 well pair. Though a number of operators have since experimented with FCDs based on the strength of the Conoco-Phillips Surmount case, as of January 2017 none has published a case history that replicates or refutes the Surmount results (Stalder 2013; Vachon et al 2015).
Abbreviations
- cSOR:
-
Cumulative steam to oil ratio
- FCD:
-
Flow control device
- HO-B:
-
Heavy oil/bitumen reserves
- ICD:
-
Inflow control devices
- NPV:
-
Net present value
- RCP:
-
Rate-controlled production
- SAGD:
-
Steam assisted gravity drainage
- SSSV:
-
Subsurface safety valve
References
Abdelfattah TA, Banerjee S, Garcia GA (2012) Effective use of passive inflow control devices to improve the field development plan. In: Proceedings of SPE deepwater drilling and completions conference, Galveston, Texas. http://dx.doi.org/10.2118/146521-MS
Achong I (1961) Revised bean performance formula for Lake Maracaibo wells. Shell Oil Company, Houston
Ajienka JA, Enaibe OE, Owolabi OO (1994) Multiphase flow metering—an evaluation of discharge coefficients. J Can Petrol Technol 33(8):57–62. doi:10.2118/94-08-07
Al-Attar HH (2013) New correlations for critical and subcritical two-phase flow through surface chokes in high-rate oil wells. SPE Proj Facil Constr 5(01):31–37. doi:10.2118/120788-pa (SPE-120788-PA)
Alimonti C, Falcone G, Bello O (2010) Two-phase flow characteristics in multiple orifice valves. Exp Therm Fluid Sci 34(8):1324–1333. doi:10.1016/j.expthermflusci.2010.06.004
Al-Khelaiwi FT, Davies DR (2007) Inflow control devices: application and value quantification of a developing technology. In: Proceedings of international oil conference and exhibition, Veracruz, Mexico. http://dx.doi.org/10.2118/108700-MS
Al-Khelaiwi FT, Birchenko VM, Konopczynski MR (2010) Advanced wells: a comprehensive approach to the selection between passive and active inflow-control completions. SPE Prod Oper 25(3):305–326. doi:10.2118/132976-PA (SPE-132976-PA)
Almeida AR (2013) A model to calculate the theoretical critical flow rate through venturi gas lift valves (includes Addendum). SPE J 16(01):134–147. doi:10.2118/126184-pa (SPE-126184-PA)
Al-Murayri MT, Harding TG, Maini BB (2011) Impact of noncondensable gas on performance of steam-assisted gravity drainage. J Can Petrol Technol 50(7–8):46–54. doi:10.2118/148943-PA
Alsafran EM, Kelkar MG (2013) Predictions of two-phase critical-flow boundary and mass-flow rate across chokes. SPE Prod Oper 24(02):249–256. doi:10.2118/109243-pa (SPE-109243-PA)
Ashford FE, Pierce PE (1975) Determining multiphase pressure drops and flow capacities in down-hole safety valves. JPT 27(9):1145–1152. doi:10.2118/5161-PA (SPE-5161-PA)
Atkinson C, Monmont F, Zazovsky AF (2004) Flow performance of horizontal wells with inflow control devices. Eur J Appl Math 15(04):409–450. doi:10.1017/S0956792504005546
Babu DK, Odeh AS (1989) Productivity of a horizontal well (includes associated papers 20306, 20307, 20394, 20403, 20799, 21307, 21610, 21611, 21623, 21624, 25295, 25408, 26262, 26281, 31025, and 31035). SPE Res Eng 4(4):417–421. doi:10.2118/18298-PA (SPE-18298-PA)
Baker RO, Fong C, Li T (2008) Practical considerations of reservoir heterogeneities on SAGD projects. In: Proceedings of SPE international thermal operations and heavy oil symposium, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/117525-MS
Banerjee S, Hascakir B (2015) Management of steam flashing in SAGD completion design via the implementation of flow control devices. In: Proceedings of SPE thermal well integrity and design symposium, Banff, Alberta, Canada. http://dx.doi.org/10.2118/178459-MS
Banerjee S, Abdelfattah TA, Nguyen HT (2013a) Benefits of passive inflow control devices in a SAGD completion. In: Proceedings of SPE heavy oil conference, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/165478-MS
Banerjee S, Jobling R, Abdelfattah TA (2013b) The role of autonomous flow control in SAGD well design. In: Proceedings of SPE annual technical conference and exhibition, New Orleans, Louisiana, USA. http://dx.doi.org/10.2118/166266-MS
Bird RB, Stewart WE, Lightfoot EN (1960) Transport phenomena. Wiley, Hoboken, p 204
Bitto R (2005) Equalizer production enhancement system, 6. Baker Hughes Inc., Houston (reprint)
Bois A-P, Mainguy M (2011) Importance of thermal consolidation of shale during SAGD process. In: Proceedings of SPE heavy oil conference and exhibition, Kuwait City, Kuwait. http://dx.doi.org/10.2118/150420-MS
Brandt AR (2012) Variability and uncertainty in life cycle assessment models for greenhouse gas emissions from Canadian oil sands production. Environ Sci Technol 46(2):1253–1261. doi:10.1021/es202312p
Butler RM, Stephens DJ (1981a) The gravity drainage of steam-heated heavy oil to parallel horizontal wells. J Can Petrol Technol 20(2):90–96. doi:10.2118/81-02-07
Butler RM, Stephens DJ (1981b) The gravity drainage of steam-heated heavy oil to parallel horizontal wells. J Can Petrol Technol. doi:10.2118/81-02-07 (PETSOC-81-02-07)
Butler RM, Yee CT (2002) Progress in the in situ recovery of heavy oils and bitumen. J Can Petrol Technol 41(1):31–40. doi:10.2118/02-01-02
Butler RM, Mcnab GS, Lo HY (1981) Theoretical studies on the gravity drainage of heavy oil during in-situ steam heating. Can J Chem Eng 59(4):455–460. doi:10.1002/cjce.5450590407
Bybee K (2008) Production operations: inflow-control devices. JPT 60(3):81–83. doi:10.2118/0308-0081-JPT (SPE-0308-0081-JPT)
Campos SRV, Balino JL, Slobodcicov I (2014) Orifice plate meter field performance: formulation and validation in multiphase flow conditions. Exp Therm Fluid Sci 58:93–104. doi:10.1016/j.expthermflusci.2014.06.018
Carpenter C (2015) The role of autonomous flow control in SAGD well design. J Petrol Technol 66(03):136–139. doi:10.2118/0314-0136-jpt (SPE-0314-0136-JPT)
Chen Q, Gerritsen MG, Kovscek AR (2008) Effects of reservoir heterogeneities on the steam-assisted gravity-drainage process. SPE Res Eval Eng 11(5):921–932. doi:10.2118/109873-Pa
Chien SF, Schrodt JLG (1995) Determination of steam quality and flow-rate using pressure data from an orifice meter and a critical flowmeter. SPE Prod Facil 10(2):76–81. doi:10.2118/24832-PA
Chow L, Butler RM (1996) Numerical simulation of the steam-assisted gravity drainage process (SAGD). J Can Petrol Technol 35(6):55–62. doi:10.2118/96-06-06
Coronado MP, Garcia L, Russell R (2009) New inflow control device reduces fluid viscosity sensitivity and maintains erosion resistance. In: Proceedings of offshore technology conference, Houston, Texas, USA. http://dx.doi.org/10.4043/19811-MS
Darby R (2001) Chemical engineering fluid mechanics. 2nd edn., rev. and expanded. Ron Darby, 2 edn. Marcel Dekker, New York (reprint)
Denney D (2015) Analysis of inflow-control devices. J Petrol Technol 62(05):52–54. doi:10.2118/0510-0052-jpt (SPE-0510-0052-JPT)
Dikken BJ (1990) Pressure drop in horizontal wells and its effect on production performance. J Petrol Technol 42(11):1426–1433. doi:10.2118/19824-pa (SPE-19824-PA)
Edmunds N (2013) Investigation of SAGD steam trap control in two and three dimensions. J Can Petrol Technol. doi:10.2118/00-01-02 (PETSOC-00-01-02)
Edmunds N, Chhina H (2001) Economic optimum operating pressure for SAGD projects in Alberta. J Can Petrol Technol 40(12):13–17. doi:10.2118/01-12-DAS
Edmunds NR, Gittins SD (1993) Effective application of steam assisted gravity drainage of bitumen to long horizontal well pairs. J Can Petrol Technol 32(6):49–55. doi:10.2118/93-06-05
Elgibaly AAM, Nashawi IS (1998) New correlations for critical and subcritical two-phase flow through wellhead chokes. J Can Petrol Technol 37(6):36–43. doi:10.2118/98-06-04
Ezeuko CC, Wang J, Gates ID (2013) Investigation of emulsion flow in steam-assisted gravity drainage. SPE J 18(3):440–447. doi:10.2118/157830-PA
Fortunati F (1972) Two-phase flow through wellhead chokes. In: Proceedings of SPE european spring meeting, Amsterdam, Netherlands. http://dx.doi.org/10.2118/3742-MS
Foster JH, Beson J, Boyle WG (1987) Wellhead equipment and flow control devices (1987 PEH Chapter 3). In: Bradley HB (ed) Petroleum engineering handbook, Chap. 3. Society of Petroleum Engineers, Richardson
Fripp ML, Dykstra JD (2013) Method and apparatus for controlling fluid flow in an autonomous valve using a sticky switch. Patent US9260952
Fripp M, Zhao L, Least B (2013) The theory of a fluidic diode autonomous inflow control device. In: Proceedings of SPE middle east intelligent energy conference and exhibition, Manama, Bahrain. http://dx.doi.org/10.2118/167415-MS
Fripp ML, Gano JC, Murphree ZR (2015) Flow control device for controlling flow based on fluid phase. Patent US7866400
Furui K, Zhu D, Hill AD (2005) A comprehensive model of horizontal well completion performance. SPE Prod Facil 20(3):207–220. doi:10.2118/84401-PA (SPE-84401-PA)
Garcia LA, Coronado MP, Peterson ER (2009) Adjustable flow control devices for use in hydrocarbon production, Google Patents (reprint). Patent US20090205834
Gates ID, Chakrabarty N (2006) Optimization of steam assisted gravity drainage in McMurray reservoir. J Can Petrol Technol. doi:10.2118/06-09-05 (PETSOC-06-09-05)
Gates ID, Leskiw C (2010) Impact of steam trap control on performance of steam-assisted gravity drainage. J Petrol Sci Eng 75(1–2):215–222. doi:10.1016/j.petrol.2010.11.014
Gates ID, Adams J, Larter S (2008) The impact of oil viscosity heterogeneity on the production characteristics of tar sand and heavy oil reservoirs. Part II: intelligent, geotailored recovery processes in compositionally graded reservoirs. J Can Petrol Technol 47(9):40–49. doi:10.2118/08-09-40
Ghesmat K, Zhao L (2015) SAGD well-pair completion optimization using scab liner and steam splitters. J Can Petrol Technol 54(6):387–393. doi:10.2118/170076-PA
Gilbert WE (1954) Flowing and gas-lift well performance. Drilling and production practice. American Petroleum Institute, Washington, D.C. (API-54-126)
Gotawala DR, Gates ID (2012) A basis for automated control of steam trap subcool in SAGD. SPE J 17(3):680–686. doi:10.2118/159170-PA
Green DW, Willhite GP (1998) Enhanced oil recovery, Vol. 6. Richardson, Texas: SPE textbook series, Henry L. Doherty memorial fund of AIME, Society of Petroleum Engineers (reprint)
Griston S, Cire FL (1989) Evaluation of two-phase steam flow through an orifice. In: Proceedings of SPE annual meeting, San Antonio, Texas, USA. Alternate evaluation of two-phase steam flow through an orifice. http://dx.doi.org/10.2118/19700-MS
Grose RD (1985) Orifice contraction coefficient for inviscid incompressible flow. J Fluids Eng 107(1):36–43. doi:10.1115/1.3242437
Halvorsen M, Elseth G, Naevdal OM (2012) Increased oil production at troll by autonomous inflow control with RCP valves. In: Proceedings of SPE annual technical conference and exhibition, San Antonio, Texas, USA. http://dx.doi.org/10.2118/159634-MS
Halvorsen M, Madsen M, Vikøren Mo M (2016) Enhanced oil recovery on troll field by implementing autonomous inflow control device. In: Proceedings of SPE Bergen one day seminar, Bergen, Norway. http://dx.doi.org/10.2118/180037-MS
Henriksen KH, Gule EI, Augustine JR (2006) Case study: the application of inflow control devices in the troll field. In: Proceedings of SPE Europec/EAGE annual conference and exhibition, Vienna, Austria. http://dx.doi.org/10.2118/100308-MS
Ihara M, Yanai K, Takao S (2013) Two-phase flow in horizontal wells. SPE Prod Fac 10(04):249–256. doi:10.2118/24493-pa (SPE-24493-PA)
Ipek G, Frauenfeld T, Yuan JY (2008) Numerical study of shale issues in SAGD. In: Proceedings of Canadian international petroleum conference, Calgary, Alberta, Canada. Alternate numerical study of shale issues in SAGD. http://dx.doi.org/10.2118/2008-150
Irani M (2013) Understanding the steam-hammer mechanism in steam-assisted-gravity-drainage wells. SPE J 18(6):1181–1201. doi:10.2118/165456-PA
Irani M, Cokar M (2016) Discussion on the effects of temperature on thermal properties in the steam-assisted-gravity-drainage (SAGD) process. Part 1: thermal conductivity. SPE J 21(2):334–352
Irani M, Ghannadi S (2013) Understanding the heat-transfer mechanism in the steam-assisted gravity-drainage (SAGD) process and comparing the conduction and convection flux in bitumen reservoirs. SPE J 18(01):134–145. doi:10.2118/163079-PA (SPE-163079-PA)
Jain R, Syal S, Long T (2013) An integrated approach to design completions for horizontal wells for unconventional reservoirs. SPE J 18(6):1026–1032. doi:10.2118/147120-PA (SPE-147120-PA)
James R (1965) Metering of steam-water two-phase flow by sharp-edged orifices. Proc Inst Mech Eng 180(1):549–572. doi:10.1243/pime_proc_1965_180_038_02
Janssen E (1967) Two-phase pressure loss across abrupt contractions and expansions, steam–water at 600 to 1400 psia. General Electric Co., San Jose, pp 13–23
Joshi SD (2003) Cost/benefits of horizontal wells. In: Proceedings of SPE western regional meeting, Long Beach, California, USA. Alternate cost/benefits of horizontal wells. http://dx.doi.org/10.2118/83621-MS
Karim RA, Goh KFG, Nuriyadi MA (2010) Horizontal well optimization with inflow control devices (ICDs) application in heterogeneous and dipping gas-capped oil reservoirs. In: Proceedings of SPE annual technical conference and exhibition, Florence, Italy. http://dx.doi.org/10.2118/133336-MS
Kojasoy G, Landis F, Kwame-Mensah P (1997) Two-phase pressure drop in multiple thick- and thin-orifice plates. Exp Therm Fluid Sci 15(4):347–358. doi:10.1016/S0894-1777(97)00003-4
Kovscek AR (2012) Emerging challenges and potential futures for thermally enhanced oil recovery. J Petrol Sci Eng 98–99:130–143. doi:10.1016/j.petrol.2012.08.004
Kyanpour M, Chen Z (2013) A new approach for designing steam splitters and inflow control devices in steam assisted gravity drainage. In: Proceedings of SPE heavy oil conference—Canada, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/165487-MS
Larter S, Adams J, Gates ID (2008) The origin, prediction and impact of oil viscosity heterogeneity on the production characteristics of tar sand and heavy oil reservoirs. J Can Petrol Technol 47(1):52–61. doi:10.2118/08-01-52 (PETSOC-08-01-52)
Lauritzen JE, Martiniussen IB (2011) Single and multi-phase flow loop testing results for industry standard inflow control devices. In: Proceedings of SPE offshore Europe oil and gas conference and exhibition, Aberdeen, UK. http://dx.doi.org/10.2118/146347-MS
Lauritzen JE, Shahreyar N, Jacob S (2011) Selection methodology for passive, active, and hybrid inflow control completions. In: Proceedings of offshore technology conference, Houston, Texas, USA. http://dx.doi.org/10.4043/21910-MS
Le Ravalec M, Morlot C, Marmier R (2009) Impact des hétérogénéités sur la production d’huiles lourdes mobiles par SAGD. Oil Gas Sci Technol—Rev IFP 64(4):469–476
Least B, Greci S, Wilemon A (2013) Autonomous ICD range 3B single-phase testing. In: Proceedings of SPE annual technical conference and exhibition, New Orleans, Louisiana, USA. http://dx.doi.org/10.2118/166285-MS
Least B, Greci S, Huffer R (2014) Steam flow tests for comparing performance of nozzle, tube, and fluidic diode autonomous ICDs in SAGD wells. In: Proceedings of SPE heavy oil conference—Canada, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/170083-MS
Lee BO, Rabeh MN, Vicario R (2013) Multi-phase (oil–water) loop flow test for helical and hybrid passive inflow control devices. In: Proceedings of international petroleum technology conference, Beijing, China. http://dx.doi.org/10.2523/IPTC-17125-MS
Li ZY, Zhu D (2010) Predicting flow profile of horizontal well by downhole pressure and distributed-temperature data for waterdrive reservoir. SPE Prod Oper 25(3):296–304. doi:10.2118/124873-PA
Li Z, Fernandes PX, Zhu D (2013) Understanding the roles of inflow-control devices in optimizing horizontal-well performance. SPE Drill Completion 26(03):376–385. doi:10.2118/124677-pa (SPE-124677-PA)
Llaguno PE, Moreno F, Garcia R (2002) A reservoir screening methodology for SAGD applications. In: Proceedings of Canadian international petroleum conference, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/2002-124
Loretz I, Hosatte P (2007) Flow control device, Google Patents (reprint). Patent US20070169942
Medina M (2015) Design and field evaluation of tubing-deployed passive outflow-control devices in steam-assisted-gravity-drainage injection wells. SPE Prod Oper 30(4):283–292. doi:10.2118/165563-PA
Mikkelsen JK, Norheim T, Sagatun SI (2005) The troll story. In: Proceedings of offshore technology conference, Houston, Texas, USA. Alternate the troll story. http://dx.doi.org/10.4043/17108-MS
Miller RW (1996) Flow measurement engineering handbook. 3rd ed. Richard W. Miller, 3rd edition. McGraw-Hill, New York (reprint)
Moen T, Asheim HA (2008) Inflow control device and near-wellbore interaction. In: Proceedings of SPE international symposium and exhibition on formation damage control, Lafayette, Louisiana, USA. http://dx.doi.org/10.2118/112471-MS
Morrow AW, Mukhametshina A, Aleksandrov D (2014) Environmental impact of bitumen extraction with thermal recovery. In: Proceedings of SPE heavy oil conference—Canada, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/170066-MS
Nasr TN, Law DHS, Golbeck H (2000) Counter-current aspect of the SAGD process. J Can Petrol Technol. doi:10.2118/00-01-03 (PETSOC-00-01-03)
Novy RA (1995) Pressure drops in horizontal wells: when can they be ignored? SPE Res Eng 10(01):29–35. doi:10.2118/24941-pa (SPE-24941-PA)
Osman ME, Dokla ME (1992) Correlations predict gas-condensate flow through chokes. Oil Gas J 90(11):43–46
Oyeka O, Felten F, Least B (2014) Screen-inflow-design considerations with inflow control devices in heavy oil. In: Proceedings of SPE heavy oil conference—Canada, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/170097-MS
Perkins TK (1993) Critical and subcritical flow of multiphase mixtures through chokes. SPE Drill Completion 8(04):271–276. doi:10.2118/20633-PA (SPE-20633-PA)
Peterson ER, Coronado MP, Garcia L (2010) Well completion applications for the latest-generation low-viscosity-sensitive passive inflow-control device. In: Proceedings of IADC/SPE drilling conference and exhibition, New Orleans, Louisiana, USA. http://dx.doi.org/10.2118/128481-MS
Pooladi-Darvish M, Mattar L (2002) SAGD operations in the presence of overlying gas cap and water layer—effect of shale layers. J Can Petrol Technol 41(6):40–51. doi:10.2118/02-06-04
Qudaihy DS, Faraj OA, Alnughaimish FN (2005) Improving horizontal well productivity using novel technology and optimization of drilling fluids. SPE Drill Completion 20(3):205–208. doi:10.2118/85332-PA (SPE-85332-PA)
Ramamurthi K, Nandakumar K (1999) Characteristics of flow through small sharp-edged cylindrical orifices. Flow Meas Instrum 10(3):133–143. doi:10.1016/S0955-5986(99)00005-9
Riel A, Burton RC, Wheeler TJ (2014) An innovative modeling approach to unveil flow control devices potential in SAGD application. In: Proceedings of SPE heavy oil conference—Canada, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/170045-MS
Ros NCJ (1960) An analysis of critical simultaneous gas/liquid flow through a restriction and its application to flowmetering. Appl Sci Res 9(1):374–388. doi:10.1007/bf00382215
Roul MK, Dash SK (2012) Single-phase and two-phase flow through thin and thick orifices in horizontal pipes. J Fluids Eng Trans ASME 134(9):091301. doi:10.1115/1.4007267
Russell RD, Garcia LA, Garcia GA (2013a) Flow control device that substantially decreases flow of a fluid when a property of the fluid is in a selected range. USA Patent No. US8403038 B2
Russell RD, Garcia LA, Garcia GA (2013b) Method of making a flow control device that reduces flow of the fluid when a selected property of the fluid is in selected range. USA Patent No. US 8403061 B2
Sachdeva R, Schmidt Z, Brill JP et al (1986) Two-phase flow through chokes. In: Proceedings of SPE annual technical conference and exhibition, New Orleans, Louisiana, USA. Alternate two-phase flow through chokes. http://dx.doi.org/10.2118/15657-MS
Sagatun SI (2010) Boundary control of a horizontal oil reservoir. SPE J 15(4):1026–1033. doi:10.2118/135534-PA (SPE-135534-PA)
Sahin B, Ceyhan H (1996) Numerical and experimental analysis of laminar flow through square-edged orifice with variable thickness. Trans Inst Meas Control 18(4):166–174. doi:10.1177/014233129601800401
Schüller RB, Solbakken T, Selmer-Olsen S (2003) Evaluation of multiphase flow rate models for chokes under subcritical oil/gas/water flow conditions. SPE Prod Facil 18(03):170–181. doi:10.2118/84961-pa (SPE-84961-PA)
Stalder JL (2013) Test of SAGD flow-distribution-control liner system in the surmont field, Alberta, Canada. J Can Petrol Technol 52(2):95–100. doi:10.2118/153706-pa
Steven R, Hall A (2009) Orifice plate meter wet gas flow performance. Flow Meas Instrum 20(4–5):141–151. doi:10.1016/j.flowmeasinst.2009.07.001
Surbey DW, Kelkar BG, Brill JP (2013) Study of subcritical flow through multiple-orifice valves. SPE Prod Eng 3(01):103–108. doi:10.2118/14285-pa (SPE-14285-PA)
Tabatabaei M, Ghalambor A (2011) A new method to predict performance of horizontal and multilateral wells. SPE Prod Oper 26(1):75–87. doi:10.2118/141164-PA (SPE-141164-PA)
Tam ES, Modien RM, Best DA (2013) The effect of production well open interval on steamflood performance. J Can Petrol Technol. doi:10.2118/88-03-07 (PETSOC-88-03-07)
Vachon GP, Klaczek W, Erickson PJ (2015) Use of flow control devices (FCDs) to enforce conformance in steam assisted gravity drainage (SAGD) completions. In: Proceedings of SPE Canada heavy oil technical conference, Calgary, Alberta, Canada. http://dx.doi.org/10.2118/174416-MS
Van Ness HC, Abbott MM (2008) Perry’s chemical engineers’ handbook, 8th edn. McGraw-Hill Professional, New York (reprint)
Vander Valk PA, Yang P (2007) Investigation of key parameters in SAGD wellbore design and operation. J Can Petrol Technol 46(06):49–56. doi:10.2118/07-06-02 (PETSOC-07-06-02)
Visosky JM, Clem NJ, Coronado MP (2007) Examining erosion potential of various inflow control devices to determine duration of performance. In: Proceedings of SPE annual technical conference and exhibition, Anaheim, California, USA. http://dx.doi.org/10.2118/110667-MS
Wang C, Leung JY (2015) Characterizing the effects of lean zones and shale distribution in steam-assisted-gravity-drainage recovery performance. SPE Res Eval Eng 18(3):329–345. doi:10.2118/170101-PA
Welch M (2011) Greener EOR: employing cogeneration to improve the energy efficiency of thermal EOR projects. In: Proceedings of SPE Asia Pacific oil and gas conference and exhibition, Jakarta, Indonesia. http://dx.doi.org/10.2118/144224-MS
Wilson A (2015) Simulation of flow-control devices with feedback control for thermal operations. JPT 66(01):69–72. doi:10.2118/0114-0069-JPT (SPE-0114-0069-JPT)
Yang GH, Butler RM (1992) Effects of reservoir heterogeneities on heavy oil recovery by steam-assisted gravity drainage. J Can Petrol Technol. doi:10.2118/92-08-03 (PETSOC-92-08-03)
Yang C, Card C, Nghiem L (2009) Economic optimization and uncertainty assessment of commercial SAGD operations. J Can Petrol Technol 48(9):33–40. doi:10.2118/09-09-33
Yuan JY, Nugent D (2013) Subcool, fluid productivity, and liquid level above a SAGD producer. J Can Petrol Technol 52(5):360–367. doi:10.2118/157899-PA
Zhang ZJ, Cai JM (1999) Compromise orifice geometry to minimize pressure drop. J Hydraul Eng 125(11):1150–1153. doi:10.1061/(Asce)0733-9429(1999)125:11(1150)
Acknowledgements
We acknowledge the financial support and the opportunity provided by the Society of Petroleum Engineering (SPE) and the Heavy Oil, Oil shales, Oil sands, and Carbonate Analysis and Recovery Methods (HOCAM) Research Team at Texas A&M University, Petroleum Engineering Department.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Banerjee, S., Hascakir, B. Design of flow control devices in steam-assisted gravity drainage (SAGD) completion. J Petrol Explor Prod Technol 8, 785–797 (2018). https://doi.org/10.1007/s13202-017-0393-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0393-4