Abstract
Surface Lower Paleozoic sandstone samples were collected from southeast central Sinai. These samples subjected to petrophysical measurements which are porosity and permeability. It is known that turbulence factor (β) is a good tool to describe turbulent flow level, hence it was used to detect the flow properties distribution that corresponds to the nature of the pore system, so turbulence factor (β) was correlated with porosity, permeability, and reservoir quality index using many equations, where porosity correlation shows the presence of three groups having same porosity ranges but correspond to different values of turbulence factor, this refers to the presence of different flow zones. Porosity–permeability relation confirmed also the presence of similar three groups, where there are nearly same porosity ranges but with different permeability values. Consequently, samples with nearly same porosity values and representing the three groups were selected for capillary pressure by mercury injection to reveal the flow properties that characterize each group. Capillary pressure results confirmed that each group has their own pore system and flow regime. Petrography was done by optical polarizing microscope (OPM) through thin sections. The results indicated that the studied sandstone is composed mainly of quartz arenite microfacies of fine, angular to subrounded, moderately well sorted monocrystalline quartz grains. There are several features indicating that the investigated sandstones have been subjected to diagenesis processes. Diagenetic events identified in these sandstones include considerable compaction during burial diagenesis at higher temperatures and low flow rates, cementation by clay minerals and iron oxides, dissolution and alteration of unstable clastic grains, and tectonically induced grain fracturing. Unstable clastic grains like feldspars suffered considerable alteration to kaolinite when exposed to meteoric water of low ionic strength near the surface. The distribution of this kaolinite rather than the post-depositional iron oxides in pores of the studied sandstone leaded to differentiating these sandstones into three different flow units. This zonation indicates that the turbulence properties are proportional to the diagenetic effects inside the pores.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
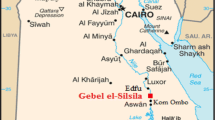
Paleozoic rocks are exposed in various regions of Egypt as south central Sinai, north Eastern Desert, and southwest Western Desert, in addition to the subsurface occurrence in north Western Desert and the Gulf of Suez. The exposed Paleozoic rock units in central Sinai have been studied by many authors, such as Issawi and Jux (1982), Jux and Issawi (1983), Klitzsch (1990), Abdallah (1992), and Wanas (2011). They identified several exposed rock units from basement upward (Table 1) as; Araba Formation of Cambrian age that attains a thickness of 170 m overlying basement complex and is essentially composed of reddish brown, fine-grained laminated sandstone and siltstone. Naqus Formation which attains a thickness of 462 m overlying the Araba Formation and is assigned to the Carboniferous age. Abu Durba Formation which attains a thickness of 166 m overlying the Naqus Formation and is assigned to Early-Carboniferous. Ataqa Formation is assigned to the Early-Carboniferous. In southeast central Sinai, west of Taba, the Araba Formation is attained 120 m thick (Table 1). The location of the studied Lower Paleozoic sandstone is shown (Fig. 1). This work tries to differentiate the studied samples according to flow regime which is a mirror image of the pore system. It is known that the pore system of a rock represents the end product of all diagenetic processes that a rock subjected to, but also uneven diagenetic effects on a rock, lead to different flow characteristics within the same facies, hence turbulence factor was selected as a petrophysical tool to detect if there are different flow systems within the studied samples or not. At first, turbulence factor is used to detect pressure loss during turbulent or non-Darcy flow in a reservoir that leads to a higher pressure gradient (to support a high flow rate through a porous medium) than that of Darcy’s equation, the deviation of the pressure gradient increases more and more as the flow rate increases, hence the lower the permeability, the more the turbulent conditions, the higher the turbulence factor and vice versa, so turbulence factor is a sensitive tool to capture permeability heterogeneity.
Location map showing the areas of exposed Lower Paleozoic rocks in central Sinai (modified after Wanas 2011)
Turbulence factor was studied and calculated by many authors, as Katz et al. (1959), Tek et al. (1962), Geertsma (1974), Noman et al. (1985), Jones (1987), and Amaefule et al. (1993). The following are the equations that estimate inertial coefficient or turbulence factor (β):
where for all equations turbulence factor (β) = ft−1, permeability (k) = mD, porosity (ϕ) = fraction.
Many correlations were done for the turbulence factor against porosity, permeability and reservoir quality index values using all the previous equations. All correlations of turbulence factor (β) with the same parameter (porosity, permeability, and reservoir quality index) using the different equations were similar to great extent hence it would be enough to display the correlation results using two equations only for this work to show that turbulence factor is a valid and reliable tool for our target, through different sources of equations, hence the equations by Jones (1987) and Amaefule et al. (1993), were selected as they just represent the latest ones among all other equations of interest. Turbulence factor-porosity correlation shows the presence of three groups that contain the same porosity range but with different values of turbulence factor. Permeability–porosity relation confirmed also the presence of those three groups where there is the same porosity range but with corresponding different permeability values. Efforts were exerted to know the reasons behind this phenomenon through petrography and capillary pressure. On the other hand, petrography described the lithofacies of the studied samples in terms of rock texture, porosity type, mineralogical composition as well as the cementing material, in addition to interpreting the diagenetic processes that affected the studied section.
Aim of study
This work aims at classifying the reservoir rocks into different flow zones based on an effective tool which is turbulence factor (β) which is a function of turbulent flow, consequently reflects the different pore systems and their relations to the microfacies diagenetic events identified in these sandstones.
Techniques
Surface Nubian Sandstone samples were collected to represent the Lower Paleozoic (Araba and Naqus formations) in southeast central Sinai, west of Taba (Table 1). The studied samples were drilled into cylindrical plugs to carry out the petrophysical measurements, where they cleaned using toluene and methanol to remove any remains of hydrocarbon and salts, respectively, then dried using a drying oven. Porosity data were measured using matrix-cup helium prosimeter (Heise Gauge type) for grain volume calculation and DEB-200 instrument that follows Archimedes principle for sample bulk volume determination. Permeability measurements of the studied samples were done using steady state permeameter. Capillary pressure by mercury injection up to 30,000 psi was performed on small samples using ‘Micromeriticsʼ apparatus, where a clean and dry sample is loaded into a glass penetrometer consisting of a sample chamber attached to a cylindrical coaxial capacitor capillary stem. The penetrometer assembly with the sample is loaded into the mercury injection apparatus and is initially filled with mercury under a vacuum. Mercury is forced into the sample at low pressure, about 1.0 psia, which is maintained until the stabilized condition is reached. The process is repeated through many pressures up to a maximum of 30,000 psia. The volume of mercury injected at each pressure is determined by the capacitance change in the capillary stem. The unsaturated pore volume is estimated as percentage of pore spaces volume that not filled with mercury at 30,000 psia. On the other hand, thin sections of the tested samples were studied using the polarized microscope to identify the microfacies in these sandstones. Thin section preparation involved vacuum impregnation with blue resin (blue-dyed epoxy) to facilitate the recognition of porosity. Special attention was paid to the porosity due to their significance in the reservoir quality evaluation.
Results and discussion
Turbulence factor behavior
The different relations displayed that the studied samples could be classified into three groups based on the turbulence factor, where (according to petrography), group (A) has the lowest percent of detrital clays, the reverse is right for group (C), while group (B) has nearly moderate percent, these groups will be discussed through the diagnostic dominating feature which is the presence of many samples having the same or nearly same porosity values but with different values of turbulence factor, either between or within the three groups. The turbulence factor-porosity relations (Figs. 2, 3) show sudden jumps of turbulence factor values for samples having nearly same porosity range between groups (A and B), (B and C), and (A and C). The previous sudden jumps revealed that we have different flow properties but corresponding to nearly same porosity range and this is most probably due to pore system nature. The turbulence factor versus permeability and reservoir quality index (Figs. 4, 5) and (Figs. 6, 7), respectively, show strong inverse correlations and also confirmed the previous different groups. The permeability–porosity relation (Fig. 8) confirmed the same behavior where at nearly same porosity range, there are sudden jumps of permeability values between groups (A and B), (B and C), and (A and C). The porosity and permeability ranges of each group are illustrated (Table 2). Also, the common porosity ranges between the three groups are displayed (Table 3), where there are common values between (A and B), (B and C), and (A and C). We tried that the common porosity ranges between the different groups to be the same for accurate comparison but 0.1 or 0.2 differences are found which are considered trivial. For example, group (A) has a porosity range of 0.222–0.241 but the equivalent one for group (B) is 0.220–0.241 hence a difference of 0.2 exists between the first limits. Also, permeability ranges (Table 3) that equivalent to the common porosity range for groups (A and B) means, for instance, the samples of that common porosity range in group (A), have permeability values vary between 362 and 6915 mD, but have values vary between 30 and 142 mD for samples in group (B).
Turbulence factor versus porosity (Jones 1987)
Turbulence factor versus porosity (Amaefule et al. 1993)
Turbulence factor versus permeability (Jones 1987)
Turbulence factor versus permeability (Amaefule et al. 1993)
Turbulence factor versus RQI (Jones 1987)
Turbulence factor versus RQI (Amaefule et al. 1993)
Capillary pressure results (Table 4) and pore size distribution of the tested samples (Fig. 9) confirm that the flow properties are quite different for the samples of same or nearly same porosity range but belong to different groups, where porosity behind large pore throats or macropores (Amaefule et al. 1993) constitute the predominate ratio and this was conducive to high permeability value (S#18, group A), in contrast to (S#61, group C) where porosity behind tight pore throats or micropores (Amaefule et al. 1993) constitute the predominate ratio and this was conducive to low permeability value. Sample (28, group B) stands between the two previous samples. The capillary pressure derived parameters that reflect the flow properties are also displayed (Fig. 9), where the highest mean hydraulic radius value (MHR) refers to the permeable group (A), and the lowest value refers to the tight group (C). The previous explanation shows that the pore size distribution (Fig. 9) was responsible for different flow properties of the samples having same porosity values.
Porosity and permeability of the studied samples were plotted again through the Winland’s flow lines (Fig. 10), to check the validity of the current classification using Turbulence Factor, the Winland’s equation that used to create these flow lines, was published by Kolodzie Jr (1980), where the distribution of the studied samples within the Winland’s flow lines (Fig. 10) shows (as the classification using Turbulence Factor method), the existing of three groups of different flow characteristics.
Petrography
Microfacies investigation usually describes the rock constituents, type of cements, pores, diagenesis, and depositional characteristics. The classification of Williams et al. (1982) was followed for the studied sandstones samples, where all impure sandstones contain 10% or more argillaceous material (such as quartz wacke, arkosic wacke, and lithic wacke) while arenites are pure sandstones which contain little or no argillaceous material (such as quartz arenite, arkosic arenite, and lithic arenite). The maturity of the sandstone increases by decreasing the percent of argillaceous matter. The variation between arkosic and lithic arenites stems from differences in source rather than any fundamental differences in process or environment of deposition. More mature sandstones are the feldspathic arenites and quartz-rich lithic arenites. Fully mature types consist essentially of quartz (quartz arenites) or quartz and abundant grains of pure chert. Most of these mature sandstones have a longer sedimentary history than the less mature rocks, usually have more than one cycle of erosion and deposition. Feldspar-rich sandstones are usually derived from granitoid igneous rocks or high-grade feldspathic gneisses or schists. The studied sandstone is mainly quartz arenite microfacies that composed of fine, angular to subrounded, moderately well sorted monocrystalline quartz grains, and porosity is mainly of intergranular type (Fig. 11). Occurrence of some dissolved feldspar areas may refer to feldspathic arenite, (Fig. 11b). The dissolution of feldspar resulted in formation of clays which form with some iron oxide, cementing materials for the rock constituents; this cement reduces to some extent, the rock porosity and permeability. This arenite microfacies is considered as mature regarding to its textural and mineralogy. The iron oxide cement has been recognized as post-depositional cement or rim cement where iron oxide grew around the quartz.
Diagenesis
Diagenetic reactions must have a thermodynamic drive so that the minerals precipitated are more stable than the minerals which are dissolving. At shallow depths and low temperatures, hydrous minerals such as gibbsite, kaolinite, and smectite form as a result of weathering or early diagenetic processes during meteoric water flow. Such early diagenetic processes may be considered a continuation of the weathering process even the pore water reduced. The overall reaction is:
These clay minerals become unstable at greater burial depth and higher temperatures, and this reaction is often referred to as reversed weathering:
The above reactions are modified from Velde (1995). The petrographic investigation of the studied sandstone reservoir of Lower Paleozoic shows that the feldspar as main primary mineral is unstable and dissolved when exposed to meteoric water of low ionic strength near the surface weathering (Figs. 11, 12). There are also several features that indicate the investigated sandstones subjected to diagenetic processes, among those are, considerable compaction during burial diagenesis at high temperatures and low rates and the pressure solution effects which results in the alteration of the original grain shapes (Fig. 12). The simultaneous cementation and pressure solution obscure the original grain shapes and resulting in concave-convex boundaries (Fig. 11), which signifies pressure solution at grain-to-grain contacts during more intense compaction upon burial, Taylor (1950). Cementations with iron oxides and clays are a common diagenetic feature in the studied sandstones. The occurrence of iron oxides as pore lining or pore filling between quartz grains indicates that they are authigenic in origin and not introduced into the pores as aggregates.
Pore system versus petrographic aspect
The petrographical description of the tested samples by the capillary pressure confirmed the pore size distribution results that produced from this test, where a compiled photomicrograph (Fig. 13), displays three different models of the pore system within the tested samples. The sample that represents group (C), shows the highest cemented nature, accompanied with the tortuous confined pore spaces (blue color) between the grains, connected through narrow throats for flow, consequently the tight, turbulent flow regime with the highest turbulence factor is the prevailing conditions for this system at the higher flow rates. The reverse is right for the representative sample of group (A), which displays the lowest cemented nature, accompanied with the spacious pore spaces (blue color) between the grains, connected through wide throats, hence the extensive, laminar flow regime with the lowest turbulence factor are the distinctive attributes for this system. The sample that represents group (B), stands midway between the previous two systems. Although the petrographic investigation revealed that one lithofacies is prevailing within the studied section, but the existence of different pore systems hence different petrophysical parameters within the same facies, reflects the uneven distribution of the diagenetic processes or effects that the studied section subjected to.
Conclusions
The petrographic investigation of the studied Lower Paleozoic sandstones from southeast central Sinai revealed that it is composed mainly of quartz arenite microfacies. Some diagenetic events are identified in this sandstone including considerable compaction during burial diagenesis at higher temperatures and low flow rates, cementation by clay minerals and iron oxides, dissolution and alteration of unstable clastic grains, and tectonically induced grain fracturing. Unstable clastic grains like feldspars suffered considerable alteration to kaolinite when exposed to meteoric water of low ionic strength near the surface. The main pore spaces in this microfacies are of intergranular type. The studied microfacies is characterized by the presence of some detrital clays, and iron oxides as cements which unequally affected the porosity and permeability of the studied rocks due to the heterogenetic distribution of these fines. Existence of different pore systems, hence different petrophysical parameters within the same lithofacies, reflects the dissimilar distribution of the diagenetic processes or effects that affect the studied section. The current reservoir clustering has been done, based on the turbulence factor which is an important petrophysical attribute studied by many authors, among them, Jones (1987) and Amaefule et al. (1993), whose equations were selected for the data layout. Turbulence factor reflects the pore system nature that represents the end product of all diagenetic processes and rock composition, so the tight flow pore system, due to intensive cementation or detrital clays or finer grain components, would exhibit much turbulence within the flow, in contrast to the wide paths pore system as a result of lesser clay content or cementing material or larger grain component, they would display laminar or less turbulent flow regime, so a clear relation between diagenesis and turbulence can be established. Turbulence factor which is a good parameter for reservoir zonation based on flow properties is strongly affected by permeability, heterogeneity, and reservoir quality index. Also, pore throat size distribution affects flow system positively or negatively, where the more the macropores, the higher the permeability, the lower the turbulence factor, and the more the micropores, the lower the permeability, the higher the turbulence factor.
References
Abdallah AM (1992) Paleozoic rocks in Egypt. Technika Poszukiwan Geologicznych. Geosynoptyka Geotermina 3:1–12
Amaefule JO, Altunbay M, Tiab D, Kersey DG, Keelan DK (1993) Enhanced reservoir description: using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells. In: 66th annual SPE conference and exhibitions held in Houston, Texas, October 3–6, 1993
Geertsma J (1974) Estimating the coefficient of inertial resistance in fluid flow through porous media. Soc Pet Eng J 14(5):445
Issawi B, Jux U (1982) Contributions to the stratigraphy of the Paleozoic rocks in Egypt. Geological survey of egypt, vol 64, p 28
Jones SC (1987) Using the inertial coefficient, (β), to characterize heterogeneity in reservoir rock. In: The 62nd annual technical conference and exhibition of society of petroleum engineers held in Dallas. TX September 27–30, 1987
Jux U, Issawi B (1983) Cratonic sedimentation in Egypt during Paleozoic. Ann Geol Surv Egypt 13:223–245
Katz DL, Cornell D, Kobayashi R, Poettmann FH, Vary JA, Elenbaas JR, Weinaug CF (1959) Handbook of natural gas engineering. McGraw-Hill Book Co., Inc., New York City
Klitzsch E (1990) Paleozoic. In: Said R (ed) The geology of Egypt, Chapter 21. A. A. Balkema, Rotterdam, p 734
Kolodzie S Jr (1980) Analysis of pore throat size and use of the Waxman–Smits equation to determine OOIP in Spindle field, Colorado. Society of Petroleum Engineers. In: 55th Annual fall technical conference, paper SPE-9382, p 10
Noman R, Shrimanker N, Archer JS (1985) Estimation of the coefficient of inertial resistance in high-rate gas wells. SPE paper no. 14207. In: Presented at the 60th annual technical conference in Las Vegas, NV, September 22–25, 1985
Taylor JM (1950) Pore space reduction in sandstones. AAPG Bull 34:701–716
Tek MR, Coats KH, Katz DL (1962) The effect of turbulence on flow of natural gas through porous reservoirs. J Pet Technol 799–806, Trans., AIME, vol 225
Velde B (1995) Origin and mineralogy of clays. Springer, New York, pp 8–42
Wanas HA (2011) The Lower Paleozoic rock units in Egypt: an overview. Geosci Front 2(4):491–507
Williams H, Turner FJ, Gilbert C (1982) Petrography, an introduction to the study of rocks in thin sections, 2nd edn. W. H. Freeman Company, Inc., San Francisco, p 626
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Elnaggar, O.M., Temraz, M.G. Lower Paleozoic reservoir zonation into different flow units using turbulence factor and their relations to diagenesis. J Petrol Explor Prod Technol 8, 351–361 (2018). https://doi.org/10.1007/s13202-017-0387-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0387-2