Abstract
Oil recovery prediction and field pilot implementations require basic understanding and estimation of displacement efficiency at the microscopic level. Glass micromodels are commonly used to determine microscopic sweep efficiency and to visualize the flow behavior. In this paper, we investigate the fingering phenomena during immiscible displacements as well as the relationship between capillary number, oil recovery, and wave characteristics of developed fingers. An etched glass micromodel with three layers of large permeability contrasts was used in this work. The fluids used include a filtered deionized water and two field oil samples. Waterflood recovery to residual oil saturation was measured through image tool analysis techniques. The results showed that the low-permeability layer resulted in higher displacement efficiency compared to the medium- and high-permeability layers. At the microscopic level, fingering phenomena are attributed for the latter finding. An early occurrence and growth of multiple fingers were observed for high-permeable layers, whereas finger growth was delayed in layers with low permeability. Peter and Flock equation was used to draw a relation between oil recovery and finger characteristics, where the increase in capillary numbers leads to a decrease in both instability scaling index and incremental oil recovery. Moreover, the limitations of Peter and Flock equation were also highlighted for strongly water-wet systems. This paper helps field operators to gain more insight into microheterogeneity and fingering phenomena and their impact on waterflood recovery estimation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction and background
Oil recovery efficiency is an interplay between different factors at the pore scale as well as at macroscale of the hydrocarbon-brine-rock system (Agbalaka et al. 2009). During different stages of oil recovery processes, unless gravity forces are predominant, the capillary and viscous forces are major driving forces of the fluids and are in competition with each other. Capillary forces are responsible for fluid entrapment, while viscous forces of the displacing phase act against capillary forces and help with oil mobility. The magnitude of capillary force is governed by interfacial tension (IFT), rock wettability, and pore geometry in which the trapped phase exists. On the other hand, viscous forces are governed by permeability of the porous medium, applied pressure drop, and viscosity of the displacing phase (Delshad et al. 1986). Review of related experiences indicates that microscopic and sweep displacement efficiencies are major factors for successful improved oil recovery (IOR) processes. Microscopic displacement efficiency is a function of capillary number. The latter is defined as the ratio of viscous-to-capillary forces, Eq. (1).
For convenience, the concept of capillary desaturation curve (CDC), the relationship between the capillary number and the residual oil saturation, has been established for various reservoir conditions. The general observation is that with increasing capillary number, the incremental oil recovery increases at both laboratory and field scales (Foster 1973; Abrams 1975; MacDonald et al. 1979; Jamaloei et al. 2010). Higher microscopic displacement efficiency is achieved by increasing capillary number (N c) over the critical capillary number (N *c ) which helps in mobilizing increased amount of trapped or residual oil.
In stable displacement conditions, a high-permeability formation usually leads to higher oil recovery compared to that of low permeability. Considering homogenous reservoir rock, higher permeability normally facilitates higher initial oil saturation, larger pore throats, and greater chance of having high primary recovery (Latil 1980). Increasing the permeability of the porous media leads to the shifting of N *c to a lower value, which in turn helps in mobilizing trapped oil blobs (Donaldson et al. 1989).
In spite of being the most popular secondary recovery methods, waterflood recovery has a major drawback of developing fingers like channels in the displacement front, which result in bypassing oil. In majority of the waterflood recovery projects, fingering/channeling phenomenon is the main cause of poor sweep efficiency and low recovery factor. This phenomenon starts to dominate the displacement process when there is a significant difference of mobility ratio between the displacing and displaced fluids (Dushin et al. 2014). The mobility ratio (M) is the ratio of the mobility of the displacing fluid (water) to the mobility of the displaced fluid (oil) and defined as:
and the mobility of a phase α (\(\lambda_{\alpha }\)) is defined as:
In immiscible displacement, occurrence of viscous fingering is believe to be due to the instability of the interface between the displacing and the displaced fluid when the mobility ratio is usually greater than 1 (Chuoke et al. 1959). This might occur when the viscosity of the displaced fluid is much larger than the viscosity of the displacing fluid or/and when the effective permeability of the displacing fluid is larger than the effective permeability of the displaced fluid. The differences in physical properties between two immiscible phases are the main trigger for frontal instability. The forces exist at the interface affecting the frontal stability includes gravity, viscosity, and (for immiscible fluids) surface or interfacial tension (Homsy 1987).
Lenormand (1985) proposed a phase diagram in which different regimes of instabilities are depicted based on mobility ratio and capillary number. It is observed that for immiscible displacement when the displacing fluid is less viscous compared to the displaced fluid, fingers form, spread across the whole network, and grow in all directions at low injection rates. The latter behavior can be best characterized using the invasion percolation (IP) theory upon which capillary fingering is dominant. On the other hand, very thin and more dendritic fingers form at higher injection rates and can be best described using the diffusion-limited aggregation (DLA) theory upon which viscous fingering is dominant.
Based on the initial work of Chuoke et al. (1959) and others, Peter and Flock (1981) proposed a numerical region to quantify the frontal instability of the interface using a dimensionless number, called the instability number (I sr) and defined as:
the value of C * depends on the rock wettability and indicates the effect of imbibition on the growth of viscous fingers. It should be noted that C * can be determined experimentally and is considered as the constant of proportionality between the effective interfacial tension (σ e) and the oil/water interfacial tension (σ), Eq. (5) (Peter and Flock 1981).
where the effective interfacial tension is a term describes the interfacial tension for a macroscopic displacement between parallel plates. In core plugs, there is less potential for fingers to grow due to the small core diameter. Therefore, the effect of instability is more prominent in real reservoir than in a linear core system. Various published data including Peter and Flock (1981) showed that when the I sr is less than 13.56, the displacement front is stable. As I sr value of the system increases, the displacement front become progressively unstable and onset of viscous fingering occurs.
To explain the recovery efficiency from unconsolidated porous media, Peter and Flock (1981) focused on the number and characteristics of the viscous fingers on the displacement front. The characteristic wavelength of the growing fingers for a rectangular porous medium is presented as:
the major assumption in the above equation is that the endpoint permeabilities are approximately equal to the absolute permeability (k) of the porous media. Finally some boundary condition for the stability of the interface was drawn based on the λ c/D value (termed as instability scaling index) where D is the diameter of the core. Through unconsolidated coreflood experiments, they have proposed that the displacement is stable for λ c/D > 1.71, unstable for λ c/D < 0.20, and the transition zone is defined in the range of 0.20 < λ c/D < 1.71. At low range of λ c/D values, many small fingers are observed and the flood front is highly unstable, whereas at higher λ c/D values, the number of fingers or waves reduces and the flood front becomes relatively stable.
Although physical interpretation of the above is obvious, Peter and Flock could not draw definite conclusion between the instability scaling index (ISI) and oil recovery. At low range of ISI, the recovery sounds to be less sensitive to λ c/D values, whereas within the boundary values, the recovery is found to be highly sensitive to the scaling index (Peter and Flock 1981).
In this study, we investigate the fingering phenomena during an immiscible displacement process in a rectangle transparent porous medium as well as the relationship between capillary number, oil recovery, and wave characteristics of developed fingers. An etched glass micromodel with three layers is used to conduct the two-phase immiscible displacement experiments. The transparent porous media helped with real-time visualization and understanding the finger growth and propagation.
Materials and methods
Materials
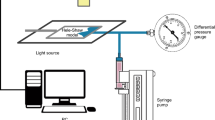
The porous media used for the study are a chamber-and-throat planar pore network fabricated by photo-etching technique (Avraam and Payatakes 1995; Ibrahim 2009; Ghazanfari et al. 2010; Mohammadi et al. 2013). The model has three bedding layers of low to high permeabilities separated by impermeable barriers. The desired channels are etched on a glass plate using hydrofluoric acid. Then, inlet and outlet ports are drilled on the etched glass plate, which is fused on to another flat glass plate at 725 °C. The dimension of each layer of the pore network is 13.6 cm × 2.8 cm representing the length and width, respectively (Fig. 1). The depth and diameter of pore bodies and pore throats were measured using a computerized optical stereo microscope (Fig. 2), and the standard falling head method is used to measure the pore properties (Fig. 3). For visualization aid, the pores were filled with colored water. Example of the 2D and 3D images analyzed and computed to determine the pore characteristics is shown in Fig. 2b, c.
In falling head drainage method, the glass micromodel was 100% saturated with colored water, held vertically, and the rate of gravity drainage and the corresponding level height of the individual layers were measured at varying hydrostatic head difference (Fig. 3). The radius of the pore throat was measured for a strongly water-wet system using the following equation (Amyx et al. 1960):
Porosity of the porous beds was measured from the difference of dry and water filled weight and also using a commercially available image analysis software, which provided the total area of the pores considering the color contrast between grains and pores. Permeability was measured by falling head method as well as normal horizontal flow using Darcy’s equation. The experimental setup used in measuring permeability is shown in Fig. 4. Outcome of these measurements is given in Table 1. From visual observation, the wettability of the pore surface is seen to be strongly water-wet (Fig. 5). Thus, throughout the experiments, water is considered as the wetting phase and the oil represents the non-wetting phase.
By using a high-precision syringe pump, the wetting phase (water) was injected in the pore network at constant flow rate through the inlet ports. Flow rates were predetermined to maintain certain minimum capillary number (N c) at certain viscosity ratio of the fluids. The absolute pressure of the wetting phase at the inlet was measured continuously with the aid of high-precision pressure transducers. Images of the pore-fluid-grain systems were captured during and after the experiments to facilitate saturation determination through image analysis.
The fluids used in this study include a filtered deionized water and two oil samples. A low-viscosity oil sample (4.3 cP) and a medium oil viscosity sample (53.6 cP) were chosen to mimic the stable and the instable displacements, respectively. The oil samples were collected from a nearby field, degassed, and filtered prior to use. Properties of the experimental fluids are given in Table 2. Because of limitations of space, only the results of the 4.3-cP oil sample are discussed in detail.
Experimental procedures
Saturation
The first stage of saturation was conducted with colorless water, followed by oil at irreducible water saturation. In this case, the oil filled pores generated black color image. The water filled pores along with transparent grain areas gave rise to white color in the image. Measurement of the area covered by the respective fluids helped in calculating the pore properties of the porous media as well as the initial oil saturation for each bedding layer.
Waterflooding and capillary desaturation curves (CDCs)
The procedure used to establish capillary desaturation curves during oil displacement with water is as follows:
-
1.
All three layers at high initial oil saturation (1-S wirr) were flooded with water at constant and low capillary number using a precision syringe pump until residual oil saturation (S or) is reached. This was ensured through constant vigilance on the produced oil volume and movement of the trapped oil blobs. The flow is stopped, and magnified displacement images were obtained for calculation of residual oil saturation.
-
2.
Recovery measurements were further initiated at higher capillary number and flow continued until no further oil is produced. Flow is stopped, photographed, and next recovery stage is initiated. This process is continued until the pressure drop reached the higher limit prescribed for the micromodel. Seven data points were obtained from low to high N c values, and the corresponding residual oil was measured. Darcy’s flow velocities of the displacing fluid, which were used later to calculate capillary numbers, were calculated using the following equation:
$$u_{i} = \frac{{q_{i} }}{{A_{i} }} = \frac{{q_{i} }}{{\left( {W.D_{{{\text{etc}},i}} } \right)}} ,$$(8)where “i” is the layer index and D etc,i is the arithmetic average of both pore body (PBDetc) and pore throat (PTDetc) depths of etching. It should be noted that in the experimental setup, a single pump was used to supply the water to all three layers (Fig. 1), and hence, there are different fluid velocities in each layer, which result in different capillary numbers in each layer. The flow rate in each layer (\(q_{i}\)) was calculated using material balance and measuring the fluid volume obtained from each layer at a certain time. Moreover, the cross-sectional area of each layer (\(A_{i}\)) varies due to the different depth of etching (Table 1).
Results and discussion
Capillary number effect
Capillary desaturation curves (CDCs) of the three layers using the 4.3-cP oil are presented in Fig. 6. These CDCs show the decreasing trend in residual oil saturation (S or) at the end of each waterflood displacement as the capillary number of the displacing fluid increased. The decrease in oil saturation is also evident from the glass micromodel images as shown in Fig. 7 for the same oil sample (4.3 cP).
For microscopic displacement, CDC is a useful experimental observation that can predict displacement efficiency at the microscopic level (Abeysinghe et al. 2012). For homogeneous porous media, a typical CDC shows constant S or at low N c. As N c increases and exceeds the critical value (N *c ), S or starts to decrease rapidly. It is important to know this N *c to mobilize trapped residual oil, which is critical for EOR and reservoir modeling. In the present case, it is evident that the critical capillary number was exceeded at the lowest water injection rate of 0.1 ml/min as the S or (for all three layers) is in a decreasing trend with increased N c of the floodwater. It is interesting to note that there is a clear trend of S or at certain N c value showing that the S or of the low-permeability layer is always the least among the three layers. Thus, it is evident that even at the microscopic level there exists a difference in displacement efficiency even at the same N c value. Tables 3 and 4 show the displacement efficiency of the three layers for the 4.3-cP and 53.6-cP oil samples, respectively. Also, Fig. 8 shows the oil recovery versus water injected pore volumes for all three layers and 4.3-cp oil sample. The latter tables and figure support the previous observation by showing higher displacement efficiency for the low-permeability layer compared to that of high permeability.
To justify this observation, the initial-residual curves (IRCs) were established for the three layers, which help in investigating the effect of heterogeneity and initial oil saturation on residual oil saturation (Stegemeier 1977). Figure 9 depicts the IRCs for the 4.3-cP oil sample where the effect of heterogeneity on residual oil saturation is more pronounced compared to initial oil saturation. The IRCs show that the high-permeability layer is the most heterogeneous among the medium- and the low-permeability layers.
Hence, the reason could be attributed to viscous/capillary fingering which takes place at the microscopic level. Photographic evidence for the growth of viscous fingers with time is captured and presented in Figs. 10, 11, and 12. These figures show that fingering is taking place faster in the high-permeability layer compared to the medium- and low-permeability layers at a particular capillary number of displacing fluid. The justification for this fingering phenomenon is related mainly to the adverse mobility ratio between the displacing and displaced fluids as well as the microheterogeneity of the glass micromodel used, which is represented by the variable pore body, pore throat, and depth of etching within the layer (Table 1).
Lenormand et al. (1983) reported that chemically etched networks on glass plates give clear observations, but the shape of the ducts is not well defined. Moreover, according to the proposed phase diagram by Lenormand (1985), the applied experimental conditions of capillary number and viscosity ratio show qualitatively that the flow regime ranges between capillary fingering at low capillary number and viscous fingering at high capillary number. Lenormand (1985) also reported that capillary fingering results in higher displacement efficiency as opposed to viscous fingering. Figure 6 shows that the same injection rate results in high capillary number in the high-permeability layer, followed by the medium- and low-permeability layers, respectively. Hence, it is most probable that viscous fingering occurred in the first layer, capillary fingering in the third layer, and transition capillary-to-viscous fingering in the middle layer.
The fingering phenomena could be observed in different degrees (Figs. 10, 11, and 12) in all the three layers, along with the wave characteristics of the fingers. The low-permeability layer has the lowest number of fingers and longest wavelength, and consequently the highest displacement efficiency. Shortest finger wavelength and largest number of fingers are observed in the high-permeability layer that displayed least displacement efficiency, in spite of the highest superficial velocity. This observation is attributed to instability of flood front, and further efforts have been given to explain the phenomena using the instability scaling index (ISI) as proposed by Peter and Flock (1981).
Instability index and recovery relation
The instability scaling index (λ c/D) was calculated using Eq. (6) for all the recovery experiments, and the results are tabulated in Tables 5 and 6 for the 4.3-cP and 53.6-cP oil samples, respectively. It should be highlighted the width of each layer in the glass micromodel (W) was used instead of (D) which corresponds to the core diameter. Detailed analysis of λ c/D values against corresponding N c and incremental oil recovery shows that as the capillary number increases, the corresponding λ c/D value decreases, and the incremental recovery reduces. This observation is in an agreement with Peter and Flock’s equation as the decrease in λ c/D, increases the instability of the front, and hence leads to lower oil recovery. Nevertheless, the proposed boundary conditions especially for the stable region are not consistent as Peter and Flock suggested an upper boundary of 1.7 instability index for a stable displacement. In our study, we observed higher values than the upper limit where the displacement was unstable and fingering occurred. This is shown clearly in Figs. 10, 11, and 12 for the 4.3-cP oil and 0.1 ml/min injection rate, where fingering occurred in the high-, medium-, and low-permeability layers at λ c/D corresponding values of 3.16, 1.85, and 1.07, respectively (Table 5).
Moreover, Fig. 13 shows that the calculated λ c/D values are the highest for the high-permeability layer and the lowest for the low-permeability layer. This indicates that the high-permeability layer is the most stable and hence higher oil recovery is expected compared to the other layers. This contradicts with our experimental observations. In all our displacement experiments, the highest displacement efficiency was obtained from the low-permeability layer and vice versa.
It is worth mentioning that there is a major difference in the experimental setup between the two cases. Peter and Flock has validated their proposed theory through 1D corefloods in unconsolidated porous media, whereas the experiments conducted here are in consolidated media in a 2D flow setup. Also, the major assumption made in Eq. (6) of replacing the water endpoint permeability with the absolute permeability (k) of the porous media is not valid here. In strongly water-wet systems, the water endpoint relative permeability is usually about 0.1 or lower, hence assuming that the effective permeability is equal to the absolute permeability would introduce erroneous and misleading results. As we discussed earlier, visualization images show that the glass micromodel used in this work is a strongly water-wet medium (Fig. 5).
Summary and conclusions
The relation between finger characteristics and oil recovery has been investigated experimentally using a heterogeneous etched glass micromodel in two-phase immiscible flow systems. The findings of this work can be summarized as follows:
-
Visual examination and quantitative measurements showed higher displacement efficiency from low-permeability layers compared to that of medium and high permeability.
-
The reason behind this finding is the instability of the oil/water interface and early occurrence of fingering. On visual observation, early occurrence and growth of multiple fingers were observed for high-permeable layers, whereas finger growth was delayed and more piston-like displacement was observed in layers with low permeability.
-
Peter and Flock equation was used to draw a relation between oil recovery and finger characteristics, where the increase in capillary numbers leads to a decrease in both instability scaling index and incremental oil recovery.
-
The limitations of Peter and Flock equation were also highlighted for strongly water-wet systems, where the use of the equation might lead to erroneous and misleading results.
Abbreviations
- C*:
-
Wettability constant
- D :
-
Core diameter (ft)
- D etc :
-
Average depth of etching (μm)
- g :
-
Acceleration due to gravity (981 cm/s2)
- k :
-
Absolute permeability (Darcy)
- k r :
-
Relative permeability
- k eff :
-
Effective permeability (Darcy)
- k wor :
-
Permeability to water at the residual oil saturation S or (Darcy)
- M :
-
Mobility ratio
- N c :
-
Capillary number
- N c * :
-
Critical capillary number
- P c :
-
Capillary pressure (Pa)
- PBDetc :
-
Pore body depth of etching (μm)
- PTDetc :
-
Pore throat depth of etching (μm)
- Q :
-
Flow rate (ft3/day)
- R :
-
Radius of etching (cm)
- S oi :
-
Initial oil saturation (%)
- S or :
-
Residual oil saturation (%)
- S wirr :
-
Irreducible water saturation (%)
- U :
-
Injection Darcy’s velocity (m/s)
- V B :
-
Bulk volume (ml)
- V p :
-
Pore volume (ml)
- W :
-
Width of the layer in glass micromodel (ft)
- ∆h :
-
Difference between the height of water in both the micromodel and the beaker (cm)
- ΔP/L :
-
Applied pressure gradient (Pa/m)
- ∆ρ :
-
Density difference between water and air (g/cc)
- μw :
-
Viscosity of water (cP)
- μ 0 :
-
Viscosity of oil (cP)
- σ :
-
Interfacial tension (dynes/cm)
- σ e :
-
Effective interfacial tension (dynes/cm)
- σair–water :
-
Air and water surface tension (72.8 mN/m at 20 °C)
- λw :
-
Mobility of the displacing fluid (water) (Darcy/cP)
- λo :
-
Mobility of the displaced fluid (oil) (Darcy/cP)
- CDC:
-
Capillary desaturation curve
- EOR:
-
Enhanced oil recovery
- IFT:
-
Interfacial tension
- IOR:
-
Improved oil recovery, incremental oil recovery
- ISI:
-
Instability scaling index
- PB:
-
Pore body
- PT:
-
Pore throat
References
Abeysinghe KP, Fjelde I, Lohne A (2012) Dependency of remaining oil saturation on wettability and capillary number. In: SPE 160883, SPE Saudi Arabia Section Technical Symposium and Exhibition
Abrams A (1975) The influence of fluid viscosity, interfacial tension, and flow velocity on residual oil saturation left by waterflood. SPEJ 15(5):437–447
Agbalaka CC, Dandekar AY, Patil SL, Khataniar S, Hemsath JR (2009) Coreflooding studies to evaluate the impact of salinity and wettability on oil recovery efficiency. Trans Porous Med 76:77–94
Amyx JW, Bass DM, Whiting RL (1960) Petroleum reservoir engineering. McGraw-Hill, New York
Avraam DG, Payatakes AC (1995) Flow regimes and relative permeabilities during steady-state two-phase flow in porous media. J Fluid Mech 293:207–236
Chuoke RL, Meurs PV, Poel CV (1959) The Instability of slow, immiscible, viscous liquid–liquid displacements in permeable media. AIME 216:188–194
Delshad M, Bhuyan D, Pope GA, Lake LW (1986) Effect of capillary number on the residual saturation of a three phase micellar solution In: SPE 14911, symposium on EOR in Tulsa
Donaldson EC, Chilingarian GV, Yen TF (1989) Enhanced oil recovery II, processes and operations, 1st edn, vol 17. Part B, Elsevier Science, pp 1–603
Dushin VR, Nikitin VF, Legros JC, Silnikov MV (2014) Mathematical modeling of flows in porous media. Wseas Trans Fluid Mech 9:116–130
Foster WR (1973) A low-tension waterflooding process. J Petrol Technol 25(2):205–210
Ghazanfari M, Kharrat R, Rashtchian D, Vossoughi S (2010) Statistical model of dispersion in a 2D glass micromodel. SPEJ 15(2):301–312
Homsy GM (1987) Viscous fingering in porous media. J Fluid Mech 19:271–311
Ibrahim AS (2009) Investigation of the mobilization of residual oil using micromodels. In: SPE 129515-STU, SPE annual technical conference and exhibition
Jamaloei BY, Ahmadloo F, Kharrat R (2010) The effect of pore throat size and injection flowrate on the determination and sensitivity of different capillary number values at high-capillary-number flow in porous media. Fluid Dyn Res 42(5):1–30
Latil M (1980) Enhanced oil, recovery edn. Technip, Paris
Lenormand R (1985) Capillary and viscous fingering in an etched network. Phys Finely Divided Matter Springer Proc Phys 5:289–294
Lenormand R, Zarcone C, Sarr A (1983) Mechanisms of the displacement of one fluid by another in a network of capillary ducts. J Fluid Mech 135:337–353
MacDonald IF, El-Sayed MS, Mow K, Dullien FAL (1979) Flow through porous media-the Ergun equation revisited. Ind Eng Chem Fundam 18(3):199–208
Mohammadi S, Maghzi A, Ghazanfari MH, Masihi M, Mohebbi A, Kharrat R (2013) On the control of glass micro-model characteristics developed by Laser technology. Energy Sour Part A Recovery Util Environ Eff 35(3):193–201
Peter EJ, Flock DL (1981) The onset of instability during two-phase immiscible displacement in porous media. SPEJ 21(2):249–258
Stegemeier GL (1977) Mechanisms of entrapment and mobilization of oil in porous media. Academic Press, New York, Improved oil recovery by surfactant and polymer Flooding, pp 55–91
Acknowledgement
The authors are grateful to the Petroleum Engineering Department, The Petroleum Institute, Abu Dhabi, for providing the laboratory facilities to conduct the laboratory experiment.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Al-Shalabi, E.W., Ghosh, B. Flow visualization of fingering phenomenon and its impact on waterflood oil recovery. J Petrol Explor Prod Technol 8, 217–228 (2018). https://doi.org/10.1007/s13202-017-0336-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-017-0336-0