Introduction

Gas flow in tight rocks has remained interest of many researchers and is extensively investigated because it plays a major role in gas reservoir engineering. Low-permeability rocks such as tight sandstone are becoming important source of natural gas, as the production from conventional hydrocarbon reserves is declining, whereas the demand is rising. Developing such low-permeability reservoirs is very challenging as the gas is held in very tight formations having poor pore connectivity. Every E&P Company’s strategy is to improve profitability and recovery. In order to achieve production at commercial rates, it is essential to understand the reservoir productivity. For performance prediction of these reservoirs, laboratory measurements are routinely conducted to characterize these low-permeability rocks. Generally, these measurements are made at different stresses, pore pressures and temperatures than are found in the subsurface. In addition, it is routine to use inert gases such as helium or nitrogen instead of methane during laboratory flow tests. So attempts are often made to correct laboratory measurements to subsurface conditions. Such corrections are complicated by several processes as the stress and pore pressure sensitivity of permeability as well as core damage.

It is generally believed that the absolute permeability of tight rocks as observed is often sensitive to the stress and pore pressure (e.g., Jones and Owens 1980; Sampath and Keighin 1982; Brower and Morrow 1985; Warpinski and Teufel 1992; Rushing et al. 2003). Several other authors have also studied about the reduction in permeability due to overburden stress, and the reduction in permeability reported by these authors is up to 90% (Thomas and Ward 1972; Jones and Owens 1980; Yale 1984; Kilmer et al. 1987). In addition, the production losses reported are up to 50% (e.g., Vairogs et al. 1971). Single-phase permeability stress sensitivity can be expressed as, i.e., k ∞ = F(σ′), where net stress, σ′, which is a combination of the relationship of pore pressure P P and confining stress σ c (e.g., Warpinski and Teufel 1992; Zoback and Byerlee 1975; Al-Wardy and Zimmerman 2004; Li et al. 2009),

$$\sigma^{{\prime }} = \sigma_{\text{c}} - n_{\text{k}} P_{\text{p}}$$
(1)

where the net stress parameter for permeability, n k, scales the effect of a pore pressure change on the effective stress. Berryman (1992), based on theory, suggested that the value n k should lie between the fractional porosity and one for a homogeneous single mineral porous medium. For sandstones, some authors experimentally found n k values in this range (e.g., Warpinski and Teufel 1992; Li et al. 2009); however, others have reported values in the order of four to six (e.g., Zoback and Byerlee 1975; Al-Wardy and Zimmerman 2004). Those authors suggested that changes in pore pressure cause compression of clay in the pores, and thereby have a larger effect on permeability. However, Al-Wardy and Zimmerman (2004) assumed that clays are around 25 times less stiff than quartz, and the data showed that the bulk modulus of typical “Gulf clays” is around 25 GPa (Han et al. 2006) which is only slightly less than 37 GPa for quartz (Carmichael 1989). It is noticeable that the samples were allowed to equilibrate for only “a few minutes” during the experiments of reported by Al-Wardy and Zimmerman (2004) and 15 min to 2 h in the experiments of Zoback and Byerlee (1975). It is therefore possible that the high values of n k were simply an experimental artifact resulting from equilibration after the confining pressure was changed.

Generally, the routine core analysis (RCA) of core plugs permeability measurements made by petroleum industry considers the confining pressure of around 2.8 MPa (API 1998). Although, the several recent publications have revealed that the permeability value obtained under these conditions can be several orders of magnitude higher than under in situ conditions for tight gas sandstone samples (e.g., Jones and Owens 1980; Brower and Morrow 1985). It is difficult to explain such large permeability reductions as a result of the stress-induced elastic closure of spherical pores (Ostensen 1983). Integration of microstructural observations with theory suggests a more likely explanation of such large stress sensitivity of permeability is due to the presence of high aspect ratio microfractures formed at grain boundaries (e.g., Ostensen 1983; Brower and Morrow 1985).

In petroleum standard industry, it has become routine to apply “overburden” adjustments to permeability data that usually been conducted at 500 psi confining stress (RCA) to make them representative of subsurface conditions. This correction to (RCA) permeability is performed using either existing empirical relationships or otherwise making measurements at in situ stress conditions on a small number of the samples of similar reservoirs, so that data would be utilized for stress correction for the core being analyzed. In the literature, enormous level of scatter on permeability plots of ambient and in situ measurements has been reported (e.g., Byrnes 1997; Byrnes et al. 2009) with the average difference in situ permeability, being on average reported is 20 times less than that measured at low stresses.

Apart from confining stress, the pore pressure could affect the measured permeability. Specifically, the slippage of gas molecules at the walls of rock pores spaces may cause additional gas flow at low pore pressures which results in a higher measured permeability (Klinkenberg 1941). Essentially, all measurements can be made at in situ stress and pore pressure, but this increases the total costs; therefore, this is not practical when development of such reservoirs is only marginally profitable.

The effect of gas slippage on permeability was reported by Klinkenberg (1941), in which the effective pore size r slip was larger than ten times the mean free path length of gas molecules, λ. The measured permeability, k a, then depends linearly on the inverse pore pressure as shown in following equation

$$k_{\text{a}} = k_{\infty } \left( {1 + \frac{b}{{P_{\text{p}} }}} \right)$$
(2)

where k ∞ is the permeability in the absence of gas slippage, and b, which we refer as the b factor, is given as

$$b = \frac{{4c\lambda P_{\text{p}} }}{{r_{\text{slip}} }}$$
(3)

where c is a parameter that depends on the geometry but is in the order of 1 (Klinkenberg 1941). The b factor is constant with pore pressure (Klinkenberg 1941), when λ is expressed as in Loeb (1934).

$$\lambda = \frac{\mu }{{P_{\text{p}} }}\sqrt {\frac{RT\pi }{2M}}$$
(4)

where μ is the gas viscosity, R the gas constant, T absolute temperature and M the molar mass of the gas.

The b factor can be found by measuring permeability at different ranges of pore pressures, and plotting permeability versus 1/P p, which often referred to as the Klinkenberg procedure (e.g., API 1998). Then the slope of the plot has been referred to as the total gas slippage (e.g., Sampath and Keighin 1982; Rushing et al. 2003). The b factor values can be used to determine slippage radius, which in combination with Klinkenberg-corrected permeabilities that can then be used to calculate permeability to different gasses at different pore pressures and temperatures (Klinkenberg 1941).

Idyllically, the Klinkenberg plots would be constructed for each individual sample and should be analyzed to derive accurate values of the b factor and to get slippage-corrected permeabilities. Although, in petroleum industry it is common practice to make a single permeability measurement at a low gas pressure and then apply a Klinkenberg correction based on empirical relationships between the b factor and permeability, or b factor and porosity and permeability (e.g., Heid et al. 1951; Jones and Owens 1980; Sampath and Keighin 1982). The latter correlations are based on the relation of the three factors to the effective pore size, r. Sampath and Keighin (1982) model the rock as a collection of cylindrical pores, where k ∞ ∝ r 4 and ϕ ∝ r 2 so that r slip r slip ∝ (k ∞/ϕ)1/2 and b ∝ (k ∞/ϕ)−1/2(e.g., Sampath and Keighin 1982). As the b factor depends on the gas used, correlations would have to be corrected for the gas used Florence et al. (2007). However, data measured with the same gas from Byrnes et al. (2009) shown a significant scatter. This will increase uncertainty when using such correlations to extrapolate to subsurface conditions.

Uncertainties in correcting for stress sensitivity and gas slippage could be partly eliminated by conducting all laboratory measurements at in situ conditions. Technically, it is difficult and extremely time consuming to use standard techniques core analysis for companies to measure permeability at in situ conditions. Maintaining controlled and stable flow makes it difficult to make steady-state gas permeability measurements at high pore pressures, and this difficultly increases as permeability decreases. To test samples under the range of drawdown conditions that would be experienced during production would further escalate the costs. In terms of economics, tight gas reservoirs are often only marginally economic so there is a drive to cut costs associated with their characterization (e.g., Baihly et al. 2010). Unfortunately, the reservoir rocks that are among the least economically viable to develop are the most expensive to characterize.

To reduce the time, and hence costs, to analyze the permeability of tight samples under in situ conditions transient techniques such as pulse-decay permeametry (Brace et al. 1968; Jones 1997) are increasingly being used by industry (Rushing et al. 2003). Generally, pulse-decay permeametry measurements are conducted using gas pressures of >2000 psi (Jones 1997). Such high pore pressures would reduce the effect of gas slippage; however, for rocks with low permeability and small pore sizes, the Klinkenberg procedure would still be required to determine the absolute permeability (Jones 1997). Jones (1997) recommended to conduct the Klinkenberg tests at pore pressures of 500, 1000 and 2000 psi. However, such recommendations do not consider either the impact that large variations in pore pressure will have on absolute permeability in stress sensitive samples. On the other hand, when a small range of pore pressures is used, the change in the apparent permeability between measurements at different pore pressures may be too low, relative to the accuracy of the permeability measurement, to determine an accurate b factor (API 1998).

Geological setting of Kirthar fold belt

The study area comprises the sedimentary rocks ranging from Triassic to Holocene (Fig. 1), and Kirthar fold belt is located in West Pakistan (Khan et al. 1986; Ahmed and Ali 1991) which is on the western zone of Indian and Eurasian Plates. This imparts a good Pab Formation (outcrop) and is thought to have good potential of hydrocarbon reserves as well as having good trapping mechanism (Umar et al. 2014). Kirthar fold belt, the Pab Formation, is part of sedimentary succession; the thick marine siliciclastic Pab Formations of Kirthar fold range from 50 to 450 m (e.g., Umar et al. 2010, 2014). These mostly consist of sandstone of interbedded with marl and mudstones. The sandstone is yellow, gray light brown and greenish, which is medium to coarse gained moderate well sorted, well rounded to subrounded (Umar et al. 2011). Marl is very thin bedded light gray and is laminated finely. It is divided into two depositional systems shallow marine, and other one is fluviodeltaic to deep marine turbidites (Umar et al. 2010).

Fig. 1
figure 1

The study area is composed of sedimentary rocks and is shown inside the map (Source: Modified from DGPC report, 2008)

Full size image

Kirthar fold belt has similarity in structural style and straight graphic equivalence to Suleiman fold belt and is trending to north–south tectonically (Khan et al. 1986). The Kirthar fold belt north–south tendering tectonic features are similar to Suleiman fold in structure and style and have stratigraphic equivalence. Kirthar fold belt from its western part connects with the Balochistan basin, and this western margin is associated with hydrothermal activities (e.g., Jadoon et al. 1994; Khan et al. 1986).

Materials and methods

For microstructure examination and mineralogy, the polished thin sections were prepared for backscatter electron microscopy (BSEM) and all samples collected from lower Indus Basin, Sindh, were examined.

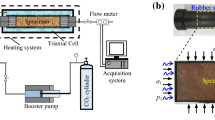
The cylindrical core plugs of ~35 mm diameter and 62 mm lengths were taken; for cleaning purpose, these samples were placed in a Soxhlet extractor using a mixture methanol–toluene and dichloromethane. The samples were dried in a humidity-controlled oven at 60 °C for 48 h prior to measurements. After thoroughly cleaning, the samples grain volume was determined using helium gas expansion porosimeter. Using caliper, the total (bulk) volume of samples was determined by measuring their diameter and length as well as the bulk volume was obtained by weighing the water-saturated sample when immersed in water using Archimedes principle. The porosity was then obtained by Eq. (5).

$$\phi = \frac{{{\text{BV}} - {\text{GV}}}}{\text{BV}}$$
(5)

Permeability measurements were made by flow of helium gas through the samples parallel to the plug axis.

For the steady-state tests, the apparent permeability k a is calculated using Eq. (6).

$$k_{\text{a}} = \frac{{2\mu L_{\text{s}} Q_{\text{a}} P_{\text{a}} }}{{A_{\text{s}} (P_{1}^{2} - P_{2}^{2} )}}$$
(6)

where μ is the gas viscosity, L s is the sample length, Q a is the flow rate at ambient pressure P a, A s is the cross-sectional area of the sample, and P 1 and P 2 are the pressures at the upstream and downstream side of the sample, respectively.

The transient permeability tests were conducted for each sample utilizing the pulse-decay permeametry facility; four tests were run for each sample to perform Klinkenberg corrections. The tests performed with different upstream gas pressures were ranging from 50 to 200 psi, and the downstream pressures were set in a way that the differential pressure should remain in between 5 and 40 psi. All measurements of the Kirthar sandstone samples were performed at different confining pressures ranging from 1000 to 5000 psi, while keeping constant temperature of 25 °C. All permeability measurements performed were corrected for slippage effects by using a straight line to estimate the b factor. Slippage corrections on all samples were performed, as these can also be very significant in low-permeability rocks.

Steady-state experiments were performed on samples with permeability larger than 0.1 mD, whereas those samples with permeability <0.1 mD were tested using pulse-decay permeametry.

Results

The permeability measurements from the Klinkenberg tests were fitted using a straight line to estimate the b factor. As recommended by the API (1998), only those tests results were considered which could be fitted to a straight line with a correlation coefficient greater than 0.95 for 4 or more data points. The b factors and k ∞ for the successful tests are shown in Table 1.

Table 1 Gas permeability and porosity measurement results of samples collected from Kirthar fold belt basin
Full size table

Effect of confining stress up to in situ stress

The absolute permeability falls as the net stress is increased as shown in Figs. 2 and 3, where net stress is given by σ′ = σ c − n k P p with n k = 1. For the steady-state and pulse-decay permeability of the samples Figs. 2 and 3, the stress sensitivity of the absolute permeability could be modeled by a power law

$$k_{\infty } = K\left( {\sigma_{\text{c}} - n_{\text{k}} P_{\text{p}} } \right)^{ - \gamma }$$
(7)

where K is the permeability extrapolated to zero net stress, γ is the stress exponent. The parameters for the different samples are given in Table 2.

Fig. 2
figure 2

Permeability as function of net confining stress

Full size image
Fig. 3
figure 3

Stress sensitivity of pore radius as calculated against each confining stress where measurements were made

Full size image
Table 2 Slippage parameters associated with confining stress
Full size table

The impact of net stress on slip radius is shown in Fig. 3. The values of slippage radius calculated from the steady-state permeability measurements showed an unexpected increase with increasing net stress for four samples. This might be the experimental artifact or error caused due to conduct of experiments; however, the Klinkenberg plots appeared linear and the absolute permeability derived from the Klinkenberg plots did decrease with increasing net stress (Table 2). For one other sample, we did observe a downward deviation in the Klinkenberg plots that indicates experimental error (Fig. 6). Therefore, these results were not included in Table 2.

The slippage radius as calculated from Eq. (3) decreased with increasing net stress in the steady-state permeability measurements, and the pulse-decay measurements Fig. 3. Klinkenberg tests at four confining stress levels on sample KTE show that for this sample both k ∞ and h slip are more sensitive to increasing net stress at low net stress levels (Figs. 3, 4).

Fig. 4
figure 4

Relationship between permeability and stress sensitivity exponents

Full size image

Effect of pore pressure during drawdown at in situ confining stress

The measured permeability increased when the pore pressure was reduced at in situ confining stress, due to increased gas slippage (Fig. 7). However, the absolute permeability k ∞ was reduced by the increase in net stress. The net effect is reduction in measured permeability with increasing net stress at low net stress levels, where slippage is low due to the high pore pressure, due to the reduction in k ∞. At lower pore pressures, higher net stresses, the increased flow due to slippage offsets the reduction in k ∞ and measured permeabilities increase.

Discussion

Influence of confining stress

The permeability stress sensitivity (Fig. 2) shows that the effect of changing the confining stress on permeability is larger at lower confining stresses. Other authors also have reported similar observations (Brower and Morrow 1985; McPhee and Arthur 1991). At low confining stresses from permeability results, it was found that this higher stress sensitivity to permeability could be the result of core damage. The samples when brought to surface experience unloading; this might result in a connected network of microfractures along the grain boundaries (Fig. 5) those results in a high permeability. As shown by Ostensen (1983), an increase in the confining stress has a greater effect on permeability dominated by microfractures or high aspect ratio pores than on round pores (Figs. 6, 7).

Fig. 5
figure 5

Core damage effect and grain boundary microfracture as observed from thin section

Full size image
Fig. 6
figure 6

Diagram shows the downward deviation in the Klinkenberg plots that indicates experimental error

Full size image
Fig. 7
figure 7

Permeability as a function of stress

Full size image

We observed the highest stress sensitivity of the Klinkenberg-corrected permeability characterized by the highest stress exponent, γ in samples KTE and KTF (Figs.  2, 3; Tables 1, 2). Microfractures can be observed between the grains of KTE and KTF sample (Fig. 5). The effect of microfractures on the permeability will depend on the pore structure of the sample. In sample KTB, we observed lesser pore connectivity with lower porosity, and in this sample the microfractures observed may conduct a higher part of the gas flow. However, the pores seem to be more connected in the more porous sample (Fig. 5) and the microfractures would have a smaller effect on the total flow. Accordingly, the stress sensitivity of this sample was found to be lowest (Table 2).

The slippage radius as calculated from the b factors values is just an indication of pore dimensions, as the gas flow model is resulting from flow in a rectangular duct with smooth walls (Beskok and Karniadakis 1999). More the flow of gas within the pores could be affected by geometry of pores as well as the surface roughness (Cao et al. 2009). Even though, the values of slippage radius as calculated at lower confining stress (Table 2) have almost similar dimensions as the width of the microfractures seen within the grain boundaries (Fig. 5). At ambient stress, it can be observed that the width of fractures is in range of μm (Fig. 8). Hence, applying in situ stress reduces slippage radius (Fig. 3), which could be consistent with a compaction of these fractures, resulting in lower permeability at these conditions.

Fig. 8
figure 8

Micro-CT shows grain boundaries closure at overburden stress (courtesy of Lithicon)

Full size image

At lower confining stresses of about 500 to 1000 psi, the Klinkenberg tests will underestimate the role of gas slippage at in situ stress, due to the stress sensitivity of slip radius. The b factor in one of the samples studied increased by a factor of 5 between 500 and 5000 psi. Whereas at 500 psi confining stress, the apparent permeability measured using pore pressure of 200 psi is within 4% error of the absolute permeability, at in situ stress, the apparent permeability is 50% greater than the absolute permeability. This supports the suggestion of Jones (1991) that Klinkenberg procedures are relevant even with the high pore pressures used in pulse-decay permeametry.

It is generally believed that the slippage factor shows the increase in gas flow due to slip proportional to Klinkenberg-corrected permeability; however, the slope of the Klinkenberg plots denotes the total contribution of slip flow to the measured permeability. Hence, some authors refer to the effect of stress on gas slippage, implying the slope rather than the b factor (e.g., Sampath and Keighin 1982; Rushing et al. 2003). The reduction in permeability and a reduction in slippage radius, which results in an increase in b factor, have contradictory effects on the slope of the Klinkenberg plot. Other authors have reported that for tight gas sandstones the slope decreases with increasing net stress (e.g., Sampath and Keighin 1982; Rushing et al. 2003), and we find this in most of the samples; however, for sample KTF an increase in the slope can be observed, due to the proportionally large reduction in slippage radius as calculated from slip parameters (Fig. 9).

Fig. 9
figure 9

Comparison of b factor and permeability data from this study and that of the Byrnes et al. (2009)

Full size image

A good correlation between the b factor and (k ∞/ϕ)1/2 is shown in Fig. 10; as discussed earlier, this would be expected due to the relation of both to the effective pore size for a cylindrical pore model. These samples have high permeabilities, but high slippage radius (Table 2). Our results of slippage factor values obtained were plotted together with that of the data collected from Byrnes et al. (2009) and have also shown consistency (Fig. 9) with the exception of KTE and KTF samples.

Fig. 10
figure 10

b factor values from the present study samples versus (k ∞/ϕ)1/2

Full size image

Funk et al. (1989) also found in carbonate rocks with a high permeability and a high b factor, small slippage calculated radius. They suggested that the high b factor was related to the presence pores with a greater than average pore size in those samples.

Other authors have submitted that the scatter seen in the relation between pore size and permeability is due to experimental error (e.g., Heid et al. 1951; McPhee and Arthur 1991). We observed that in few samples there was an increase in the value of slippage radius with increase in net stress, contrary to the other samples tested here (Fig. 5), and in tests on another sample we observed that measured permeability decreased more than linearly with increasing pore pressure. This would result in a higher b factor and a low slip radius.

Other authors have also noted that the Klinkenberg plot becomes steeper at high pore pressures (Klinkenberg 1941; Ertekin et al. 1986; McPhee and Arthur 1991). Ertekin et al. (1986) suggested that the downward curvature is related to the difference between ideal gas behavior and the properties of a real gas. The b factor would no longer be constant as the viscosity and compressibility of the gas are a function of pore pressure. However, a change in gas properties would be observable in all tests, which was not the case in our tests. The effect suggested by Ertekin et al. (1986) may be more significant for larger gas molecules, such as hydrocarbons, whereas helium was used in this study.

Inertia effects at high pore pressures may lead to higher energy losses, resulting in a downward deviation on the Klinkenberg plot (McPhee and Arthur 1991); similarly, we also observed the downward deviation in one of the samples as shown in (Fig. 6). Some other authors have also suggested that the presence of pore scale heterogeneity can cause the inertial energy losses at lower flow velocities (Noman and Archer 1987). This supports the suggestion that experimental artifacts are the cause of the observed increase in slippage radius with increasing net stress (Fig. 3) and the position of samples KTG and KTC as outliers in Fig. 9. This suggests that the b factors obtained may reflect experimental error despite the linear Klinkenberg plot with a correlation coefficient greater than 0.95 for four data points as recommended by API (1998).

Conclusion

We performed experiments on tight sandstone samples at different stress conditions to define the gas slip parameter and to evaluate an effective pore size from these results. The stress sensitivity of the absolute gas permeability was characterized by permeability measurements covering a range of confining stresses. In addition, the effect of gas slippage and permeability reduction during pressure depletion was investigated by reducing pore pressure at in situ confining stress. Following observations were made:

  1. 1.

    It was observed from experimental results conducted that at lower confining stresses, the permeability of the samples studied showed high stress sensitivity, whereas at higher confining stresses the permeability was less stress sensitive. This could be due to reversible core damage, as we observed microfractures at grain boundaries in thin sections of the samples.

  2. 2.

    The stress sensitivity observed was larger in samples that had a small connected pore volume. The effective pore size was calculated from the gas slip parameter; at low confining stress levels, this value was in the same order of magnitude as the microfracture width. The pore size calculated from gas slippage was reduced at higher stress levels, which could indicate a closure of microfractures.

  3. 3.

    A pore pressure reduction at in situ stress initially reduced the measured permeability by increasing the net stress and thus reducing the absolute permeability. As pore pressure was reduced further, the increased contribution of gas slippage increased in the measured permeability. This indicates that large drawdowns would enhance the rate of gas production in these reservoirs.