Abstract
In this paper, we introduce an L-system based on the fractal geometry to study complex fracture networks. Comparing with other simulation models, the fractal fracture could not only maintain the bifurcation of the fracture geometry but also represent the multi-level feature of the complex fracture networks according to its fractal characteristics. Since the fractal geometry is always connected with several controlling parameters, the factors affecting on the fracture propagation can be quantized. With the fractal fractures, further studies on the fracture geometry and the multi-leveled branches are carried out, and the results can be concluded as: (1) when the complex fracture geometry is considered, the influence of the connectivity and complexity of the fracture network on the well performance is hard to ignore, and enhancing the connectivity and complexity of the fracture network will perform better than making a long but disconnected fracture on the shale gas development; (2) of a multi-leveled fracture network, the main fractures near the horizontal well contributes to the initial production, but the conductivity ratio (conductivity of the secondary fractures versus the conductivity of the main fractures) influences the decline rate, so a high production rate cannot be maintained without an efficient contributing area covered with conductive secondary fractures.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Duo to the low permeability and porosity, economic development of the shale gas resources always needs a multistage hydraulic fracturing. Different from the traditional bi-wing hydraulic fractures, complex fracture networks are generated near the horizontal wells in the shale gas reservoirs, as monitored by microseismic events (MSE) (Fisher et al. 2002; Maxwell et al. 2002; Daniels et al. 2007). Mine-back experiments and some field observations (Huang and Kunsoo 1993; Mayerhofer 2006) suggest that hydrofractures do not propagate linearly; when the reservoir is rich in natural fractures (NFs), the hydraulic fractures (HFs) may be created multi-branched. And it is mentioned that the complexity of the fracture networks is the main factor differing from the bi-wing fractures that contributes to the well production (Jang et al. 2015).
Considering the complex geometry, width of the branches of the fracture network is smaller than a single bi-wing fracture, the proppant might not be able to transport to the tip of the total fracture network (Xu et al. 2009), and this leads to a multi-level feature of the fracture networks which has a significant influence on the well performance. Analytical methods such as rate transient analysis (RTA) and well logging both show that the critical zone of the stimulated reservoir is smaller than the total area monitored by MSE (Friedrich 2013; Rahimi et al. 2014). The complexity and connectivity are two key parameters of the fracture networks, they relate directly with the well production, and it is obvious that the complexity and connectivity of the fracture network near the horizontal well are higher (Jones et al. 2013; Chen et al. 2016).
For better studying the performance of the fracture networks, analytical and numerical methods are applied. Olsen et al. studied the interactions between HFs and NFs and introduce a method to characterize the propagation of the complex fracture network considering the heterogeneity of the reservoir and the irregular distribution of natural fractures (Olson 2008; Olson and Arash 2009). Besides the analytical studies, numerical models are developed for further study and engineering simulation. The dual-porosity model, wiremesh model and unconventional fracture model (UFM) are three typical numerical models that can take the main characteristics of the fractures into consideration when simulating a complex fracture network. Dual-porosity model is first introduced by Warren and Root (Warren and Root 1963) to characterize the behavior of naturally fractured reservoirs and now widely applied in fracture modeling (Zimmerman et al. 1993; Du et al. 2010; Cipolla et al. 2010). The stimulated region is regarded as dual porosity or even multi-porosity, and the properties of the grids can be assigned independently. The wiremesh model is consisted of two perpendicular sets of vertical planar fractures, and it quantizes the complicated geological and engineering factors to the parameters controlling the propagation of the wiremesh network (Xu et al. 2009; Xu et al. 2010; Meyer and Lucas 2011). The properties of the planar fractures and their spacing are related to different engineering parameters even MSE, and the mechanical interactions between the fracturing fluid and fracture walls are its main consideration (Xu et al. 2010; Weng et al. 2011). However, the models above cannot display the fracture geometry and that is the reason UFM is developed (Weng et al. 2011; Weng 2015). The UFM mainly studies the interactions between the HFs and NFs and details the propagation of the fracture network within the unstructured grids. It couples the fracture geometry with the factors influencing the propagation such as the orientation of the NFs and the rock deformation.
In fact, of either wiremesh model or the UFM, the main focus is the description on the fracture propagation; the conceptual models mentioned by Jones et al. (2013), Chen et al. 2016), studying the influence of the fracture complexity and connectivity on the typical production curves, fail to consider the fracture bifurcation. So in this paper, we would like to introduce a method based on the fractal geometry theory to characterize the fracture network and to analyze the well performance. The fractal geometry theory was put forward by Mandelbrot (1979) and has been applied to rock mechanics since 1982 (Xie 1993; Wang et al. 2015a, b) utilized the iterated function system (IFS) to study the bifurcation performance of the fracture network. According to the fractal geometry theory, the fracture network we generated can be both bifurcated and multi-leveled, the fracture geometry can be related to few fractal controlling parameters, and these lead to the main advantages of the model: (1) characterizing the bifurcation feature of the fracture geometry; (2) quantifying the connectivity and complexity of the fracture network for analyzing; and (3) classifying the fractures into different levels to differ the main fractures and secondary fractures.
Fractal fractures based on the L-system
Characterization of fractal fracture model
L-system is a rewriting system that defines a complex object by replacing parts of the initial object according to rewriting rules, and it simulates development rules and topological structure well (Lindenmayer 1968; Han 2007). The system has the feature of self-adjusting when something bifurcates, and this feature can describe the growth of trees. However, in this paper, we first introduce the L-system into fracture characterization because a fracture also has similar development rules and topological structure as trees and the interaction between HFs and NFs could be regarded as a type of rule-adjusting procession affecting the propagation of the fracture, which coincides with the basement of the L-system.
Four key parameters control the generation of a fractal fracture. They relate closely to the fractal fracture geometry which influences the performance of the production wells:
-
1.
The fractal distance (d) mainly controls the extending distance of the fractal fractions, it relates closely to the half-length of the fracture obtained by MS monitoring, and the influence of the fractal distance is shown in Fig. 1.
-
2.
The deviation angle (α) controls the orientation when the fracture deviates or generates a secondary branch; it relates to the area of the stimulated reservoir, and when cooperating with the fractal distance, the size of the fractal fracture network can be adjusted for matching. Figure 2 shows the influence of the deviation angle on the orientation of the branches.
-
3.
The number of iterations (n) controls the growth of a fractal fracture network. It depends on the complexity of the fracture network or the density of the MS events. This parameter relates to the multi-level feature of the fractal branches: in each iteration, the fractal fractures propagate from the original nodes following the given generating rules to construct part of the network. It is now considered that during the actual stimulating procession, the secondary fractures extend on the basis of the main fractures, so with this similarity, levels of the fractal fractures are also distinguished based on the generating orders according to the iteration times.
-
4.
There are rules for controlling the growth of the bifurcation. To account for an irregular propagation mode of a complex fracture network, the rules for controlling are always preset as more than three. In conjunction with the iteration times, the fractal fracture model could model numerous fracture geometries under different conditions. And by adjusting the combination of the growth rules, the value of the fractal distance and deviation angle, the fractal fracture model can generate the best fractal geometry matching the given fracture network.
Geometry calibration with L-system
The generating rules preset the basement to match or to generate a fracture pattern. It is recognized that the fracture network is generated from the interaction between HFs and NFs. When a hydraulic fracture interacts with a natural fracture, three cases are concluded to happen as shown in Fig. 3: crossing, terminating or offsetting (Huang et al. 2015a, b). So the generating rules are preset to characterize these three cases, and each case could be differed into different situations if a high matching accuracy is asked for.
To represent the cases, we may preset the generating rules as shown in Fig. 4. The cases “Crossing” and “Terminating” can be simplified as a straight line, and to represent the case “Offsetting,” at least three cases are necessary. The generating rules can be adjusted by changing the length or the deflection angle. But as we have mentioned before, presetting too much generating rules is not necessary since what we want is a fractal fracture geometry with multi-level feature and following the extending tendency of the fracture network.
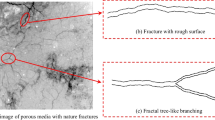
Two simple applications are carried out to illustrate the matching effect of the fractal fractures: Fig. 5a is a typical fracture obtained from the mine-back experiments, the main trunk is first matched with the combination of the generating rules, and by increasing the iteration times, the fractal fractions are generated from the main trunk as shown in Fig. 5c, and the obtained fractal geometry not only follows the extending tendency of the actual fracture but also maintains the fractal characteristics.
Fracture obtained from mine-back experiments and its matching patterns. a Comes from the experiments of Huang and Kunsoo (1993), and b and c are the corresponding fractal fractures obtained in this paper
To match the fracture geometry in the shale gas reservoirs, the MSE can be introduced as the constraints since it is the most significant and common used information about the fracture network. Figure 6 shows an application of the fractal geometry on characterizing the fracture network according to the MSE, and the green signals are pointed to represent different situations. Taking the total distance between the MSE and the nodes of the fractal pattern as the final optimization object, the fractal pattern is randomly generated by adjusting the fractal distance, the turning angle and the combination of the generating rules until the error limit is reached. The results show that the fractal geometry could also match the propagating tendency of the fracture network calibrated by MSE.
Simulation workflow
To convert the fractal geometry to the well performance, we put forward a workflow shown in Fig. 7. The fracture network geometry is generated and discretized into 2D grids to represent the conductive fractures contributing to the production. With this simulation workflow, the fractal fracture geometry can be converted to the conductive fracture network with any simulator, and in this paper, we use E300 simulator of Eclipse for numerical simulation.
Well performance analysis based on a case study
The fractal fracture model (FFM) could analyze the influence of either individual fractures or the integral fracture geometry on the well production. In this part, we would like to study the influence of the multi-leveled fractures, fracture geometry and conductivity ratio, which are rarely analyzed before, on the well performance based on the fractal fracture model.
The analysis is carried out based on a case study. The simulation data and production data are simplified from a shale gas reservoir of China as listed in Table 1. The fractal controlling parameters and the fractal geometry are obtained by history matching under the limitation of the fracture monitoring data. The fractal fracture geometry of each half-wing is taken as the same, and the matching results are shown in Fig. 8.
Multi-level feature of fractal fracture network
According to the multi-level feature of the fractal geometry, fractal fracture network has its advantage on classifying the fractures into different levels. Taking the fracture network in Fig. 8 as an example, three more iterations have been done to generate the responding fractal pattern, so the network is divided into 3 levels with their synthesized length and covering area shown in Fig. 9, and the cumulative production of each pattern is also compared.
The production comparison shows that there is a great enhance on the well production when the fracture network on level 3 is utilized for simulation. However, the growth on the length and the covering area from level 2 to level 3 are both smaller than those from level 1 to level 2. It is assumed that the difference comes from the development on the connectivity and complexity of the fracture network. To demonstrate the assumption, we try to adjust the length and the covering area of other two levels to match level 3 and compare their production data as shown in Fig. 10.
According to the simulation results, daily production rate of level 1 soon goes down and its cumulative production is far smaller than that of the other two. The low complexity of level 1 cannot provide a high production, and it also demonstrates that the bi-wing fracture is hard to fit the fracture modeling in shale gas reservoirs. Daily production rate of level 2 is similar to that of level 3, but it also soon goes down, resulting in the difference on their cumulative production, demonstrating that when the complexity of the fracture network is large enough, it will not influence the initial production rate, but it still influences the decline rate of the production curves.
Influence of the fracture geometry on the well production
As we have discussed, the complexity of the fracture network is critical to the well production; however, with the different fractal fracture geometry, how could we evaluate the fracture performance? We generate four fractal fracture networks by combining different generating rules with the same fractal distance and deviation angle as shown in Fig. 9 to run for simulation, and the patterns and the simulated results are compared in Fig. 11 (lines in black are the main structure of the network, and the lines in blue are their fractions).
Comparing the fracture geometry and production data of patterns (a), (c) and (d), the final production drops with the reduction in the fracture connectivity, although the synthesized length of the fracture increases. So when the complex geometry of the fracture network is considered, the fracture connectivity performs a more critical influence on the well performance than the facture half-length. Combined with the conclusion we drawn before, the efficiency of the fracture network, related to the complexity and connectivity, is a determining factor to the well production, and only considering the increase on the fracture half-length in the shale gas development may contribute little to the final recovery. On the other hand, both pattern (a) and pattern (b) are low in connectivity and production, but the final production of pattern (a) is higher, showing that the synthesized half-length of the fracture network is still positive to the fracture performance.
Influence of the conductivity ratio on the well production
In the actual production, the conductivity of the fracture network is proved to be different, and there are several main fractures with higher conductivity and secondary branches with relatively lower value. The conductivity ratio (conductivity of secondary branches versus the main fractures) is also an important factor to determine the fracture performance. To analyze the influence of the conductivity ratio on the well production, we take the main structure in Fig. 9 as the main fractures, and the fractures in level 3 as the secondary branches, the conductivity ratio is given as 1:1–1:100, and the comparison with the actual production is shown in Fig. 12.
-
1.
The initial production is almost the same. Since the pressure wave does not spread to the secondary branches, the main fractures of the network determine the early production.
-
2.
With the ratio changes and the conductivity of secondary fractures turns down, the decline rate of the production curves increases. So the decline rate, which is a key factor to maintain the high production rate, is connected directly with the overall effect of fracturing.
-
3.
The contribution of the secondary branches maintains a great proportion to the well production, so in the hydraulic fracture network simulation and in the actual fracturing design, only concerning the stimulated results of the main fractures without optimizing the secondary fractures may finally result an inefficient stimulated reservoir area and a low level of production.
Conclusions
-
In this paper, a novel fracture model based on the fractal geometry is introduced, we detail the fractal controlling parameters and their influence on the fracture geometry, and two simple matching cases present that the fractal fracture could be utilized to match either the rock fractures or the fracture network in the shale gas reservoirs.
-
The factors affecting on the fracture propagation can be quantized into several fractal controlling parameters, the fractal fracture can be divided into different levels according to the iteration times, and these are two advantages of the fractal fracture differing from other normal fracture models.
-
With the features of the fractal fractures, further studies on the influence of the fracture geometry and the conductivity ratio of the fracture network on the well performance are carried out, and we obtain the following conclusions: (1) considering the complex fracture geometry, the complexity and connectivity of the fracture network perform a obvious influence on the well production, and (2) the secondary fractures also contribute greatly to the fracture performance. The conductivity ratio mainly influences the decline rate, and it is not sensible to concern over the synthesized fracture half-length of the covering area without considering the contributing efficiency of the fracture network during the fracturing design.
References
Chen Z, Liao X, Zhao X, Lv S, Zhu L (2016) A semianalytical approach for obtaining type curves of multiple-fractured horizontal wells with secondary-fracture networks. Soci Pet Eng. doi:10.2118/178913-PA
Cipolla CL et al (2010) Reservoir modeling in shale-gas reservoirs. SPE Reserv Eval Eng 13(04):638–653
Daniels JL et al (2007) Contacting more of the barnett shale through an integration of real-time microseismic monitoring, petrophysics, and hydraulic fracture design. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Du CM et al (2010) Modeling hydraulic fracturing induced fracture networks in shale gas reservoirs as a dual porosity system. In: International oil and gas conference and exhibition in China. Society of Petroleum Engineers
Fisher MK et al (2002) Integrating fracture mapping technologies to optimize stimulations in the Barnett Shale. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Friedrich M (2013) Determining the contributing reservoir volume from hydraulically fractured horizontal wells in the Wolfcamp formation in the Midland Basin. Unconventional resources technology conference (URTEC)
Han J (2007) Plant simulation based on fusion of L-system and IFS. Computational science—ICCS 2007, pp 1091–1098
Huang J-I, Kunsoo K (1993) Fracture process zone development during hydraulic fracturing. In: International journal of rock mechanics and mining sciences and geomechanics abstracts, vol 30, No. 7. Pergamon
Huang J et al (2015a) Natural-hydraulic fracture interaction: microseismic observations and geomechanical predictions. Interpretation 3(3):SU17–SU31
Huang J et al (2015b) Natural-hydraulic fracture interaction: microseismic observations and geomechanical predictions. Interpretation 3(3):SU17–SU31
Jang Y et al (2015) Modeling multi-stage twisted hydraulic fracture propagation in shale reservoirs considering geomechanical factors. In: SPE eastern regional meeting. Society of Petroleum Engineers
Jones JR, Richard V, Wahju D (2013) Fracture complexity impacts on pressure transient responses from horizontal wells completed with multiple hydraulic fracture stages. In: SPE unconventional resources conference Canada. Society of Petroleum Engineers
Lindenmayer A (1968) Mathematical models for cellular interaction in development. J Theor Biol 18:280–315
Mandelbrot BB (1979) Fractals: form, chance and dimension. In: Mandelbrot BB (ed) Fractals: form, chance and dimension. WH Freeman & Co., San Francisco, p 1 (16 + 365)
Maxwell SC et al (2002) Microseismic imaging of hydraulic fracture complexity in the Barnett shale. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Mayerhofer MJ et al (2006) Integration of microseismic-fracture-mapping results with numerical fracture network production modeling in the Barnett Shale. In: SPE annual technical conference and exhibition. Society of Petroleum Engineers
Meyer BR, Lucas WB (2011) A discrete fracture network model for hydraulically induced fractures-theory, parametric and case studies. In: SPE hydraulic fracturing technology conference. Society of Petroleum Engineers
Olson JE (2008) Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight gas sands. The 42nd US rock mechanics symposium (USRMS). American Rock Mechanics Association
Olson, JE, Arash DT (2009) Modeling simultaneous growth of multiple hydraulic fractures and their interaction with natural fractures. In: SPE hydraulic fracturing technology conference. Society of Petroleum Engineers
Rahimi ZA et al (2014) Correlation of stimulated rock volume from microseismic pointsets to production data-A horn river case study. In: SPE Western North American and Rocky Mountain joint meeting. Society of Petroleum Engineers
Wang W et al (2015a) A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. J Nat Gas Sci Eng 23:139–147
Wang W, Su Y, Zhang X, Sheng G, Ren L (2015b) Analysis of the complex fracture flow in multiple fractured horizontal wells with the fractal tree-like network models. Fractals 23(2):1550014
Warren JE, Root PJ (1963) The behavior of naturally fractured reservoirs. Soc Petrol Eng J 3(03):245–255
Weng X (2015) Modeling of complex hydraulic fractures in naturally fractured formation. J Unconv Oil Gas Resour 9:114–135
Weng X, Kresse O, Cohen CE, Wu R, Gu H (2011) Modeling of hydraulic-fracture-network propagation in a naturally fractured formation. SPE Prod Oper 26(04):368–380
Xie H (1993) Fractals in rock mechanics. Crc Press
Xu W, Le Calvez JH, Thiercelin MJ (2009) Characterization of hydraulically-induced fracture network using treatment and microseismic data in a tight-gas sand formation: a geomechanical approach. In: SPE tight gas completions conference. Society of Petroleum Engineers
Xu W, Thiercelin MJ, Ganguly U, Weng X, Gu H, Onda H, Sun J, Le Calvez J (2010) Wiremesh: a novel shale fracturing simulator. Soc Pet Eng. doi:10.2118/132218-MS
Zimmerman RW et al (1993) A numerical dual-porosity model with semianalytical treatment of fracture/matrix flow. Water Resour Res 29(7):2127–2137
Acknowledgments
This work was supported by the National Basic Research Program of China (2014CB239103) and Graduates’ Innovation Foundation of China University of Petroleum (East) (YCXJ2016020). The authors would like to acknowledge the technical support of ECLIPSE in this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhou, Z., Su, Y., Wang, W. et al. Application of the fractal geometry theory on fracture network simulation. J Petrol Explor Prod Technol 7, 487–496 (2017). https://doi.org/10.1007/s13202-016-0268-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-016-0268-0