Introduction

Markov process was firstly introduced by Russian mathematician, Andrei Andreyevich Markov, in 1907. Markov-based algorithm, like Markov chain Monte Carlo (MCMC) simulation, has recently been used to quantify uncertainty in infill well placement in the field of petroleum exploration and production (Arinkoola et al. 2015). Spatial Markov chain (SMC) models have also been widely adopted in petroleum reservoir to characterize the spatial heterogeneity of categorical variables through the conditional probabilities (transition probabilities) from different directions (Carle and Fogg 1997; Weissmann and Fogg 1999). At present, there are two kinds of different independent assumptions to simplify the conditional probability of SMC models: one is full independence assumption; the other is conditional independence assumption. The full independence assumption is defined by Elfeki and Dekking (2001), and the corresponding conditional probability formulas are proposed by Elfeki and Dekking (2001) and developed by Li et al. (2012). A spatial Markov chain with full independence assumption consists of several one-dimensional Markov chains, which are forced to move to the same location with equal states. The full independent assumption caused the small class underestimation problem. This method is feasible only for enough conditional data. The conditional independence assumption can be found in Pickard random field in cardinal directions (Pickard 1980), and its general definition is suggested by Li (2007), i.e., given a cell, its nearest neighboring states are conditionally independent. The general conditional probability formulas are given by Li (2007), which do not have the small class underestimation problem.

An SMC is actually a dimensionality reduction process where its multi-dimensional conditional probabilities are expressed as multiple one-dimensional transition probabilities. The transition probabilities of reservoir categorical variables, such as lithofacies, can be estimated from well data. The vertical transition probabilities can be estimated by the vertical transition tallies from well logs. The transition probabilities in other directions can be estimated by the Walther’s law (Li et al. 2012). Most traditional geostatistical models, like Markov chain random field (MCRF), use well data only and make prediction based on SMC, which results in a relatively low prediction accuracy (Huang et al. 2016a). Huang et al. (2016b) introduced a beta-transformed Bayesian updating model to boost the classification accuracy of category random field. Auxiliary information, however, has not been taken into consideration. To make use of secondary data, such as geophysical well logs, Eidsvik et al. (2004) used hidden Markov chains for estimation of geological attributes. The hidden Markov chain uses Dirichlet prior distributions for the Markov transition probabilities between rock types. Li et al. (2010) developed the Markov chain models by integrating multi-scale information, such as logging, core data and seismic data. In the remote-sensing area, Li et al. (2015) introduced a Bayesian MCRF cosimulation method for improving land cover classification accuracy. We propose a single spatial hidden Markov chain (SHMC), which improves the accuracy of reservoir modeling by integrating geological conceptual data with well data.

Review of Markov models

Markov mesh model

A petroleum reservoir grid is a finite, regular grid in one to three dimensions, and its gridding cells are indexed by a positive integer s, where s takes on values in \(S = \{ 1,2, \ldots ,n\}\). All cell states \(F = \left\{ {F_{1} ,F_{2} , \ldots ,F_{n} } \right\}\) can be regarded as a family of random category variables defined on the set S; each random variable \(F_{s}\) takes a state value \(f_{s}\) in the state set \(\varOmega = \{ 1,2, \ldots ,m\}\). If all cell states \(F_{1} ,F_{2} , \ldots ,F_{n}\) follow a sequential path, it is defined as a spatial stochastic sequence. A set of reservoir category variables F can be considered as a Markov random field or a Gibbs random field, and its joint probability (likelihood function) generally takes the following form (Tjelmeland and Besag 1998; Salomão and Remacre 2001)

$${ \Pr }(f) = \frac{{\exp \left\{ { - \sum\nolimits_{s = 1}^{n} {\sum\nolimits_{{j \in \eta_{s} }} {\varPsi (f_{s} ,f_{j} )} } } \right\}}}{{\sum\nolimits_{f} {\exp \left\{ { - \sum\nolimits_{s = 1}^{n} {\sum\nolimits_{{j \in \eta_{s} }} {\varPsi (f_{s} ,f_{j} )} } } \right\}} }}$$
(1)

where \(\eta_{s}\) is a set of cells which is adjacent to s; \(\varPsi \left( {f_{s} ,f_{j} } \right)\) denotes the relationship between cell s and cell j; \(f = \left\{ {f_{1} ,f_{2} , \ldots ,f_{n} } \right\}\) is a configuration of F, corresponding to a realization of the field. The use of Eq. (1) for the simulation of reservoir category variables is theoretically feasible, but it is actually limited by the highly time consuming in computation. By the best-known classical approximation, Eq. (1) can be simplified as Blake et al. (2011) suggested

$${ \Pr }(f) = \prod\limits_{s = 1}^{n} {\Pr } \left( {f_{\text{s}} |f_{{\eta_{\text{s}} }} } \right)$$
(2)

where \(f_{{\eta_{s} }} = \{ f_{r} \left| {r \in \eta_{s} } \right.\}\) stands for the set of state values at the cells neighboring s.

Markov mesh models (Stien and Kolbjørnsen 2011) are fully specified through the conditional probabilities in RHS of Eq. (2) as

$${ \Pr }\left( {f_{s} |f_{{\eta_{s} }} } \right) = { \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} ,f_{{s_{2} }} , \ldots ,f_{{s_{l} }} } \right)$$
(3)

where \(s_{1} ,s_{2} , \ldots ,s_{l}\) is its nearest known locations of current cell s in different directions; s − 1 is always the start cell of the Markov chain to the unknown cell s, which is to be estimated. The probabilities in Eq. (3) are defined through logit link functions in generalized linear models, and Markov mesh can use larger cliques or neighborhood to capture complex interclass relationships. Recently, Stien and Kolbjørnsen (2011) proposed the method of a fast estimation through iterated weighted least squares and fast simulation through a unilateral path. Kolbjørnsen et al. (2014) recommended using multiple grids in Markov mesh facies modeling, which is typically ten times faster than that of creating one SNESIM realization. Although Markov mesh model is widely used in geoscience, the parameter estimation and iteration process are annoying.

Spatial Markov chain models

Spatial Markov chain models use the full independence assumption and the conditional independence assumption to define the conditional probability for simplifying the complex computation in Eq. (3). It is actually a dimensionality reduction process where its conditional probabilities \(\Pr \left( {f_{s} |f_{{\eta_{s} }} } \right)\) are expressed as multiple one-dimensional transition probabilities from different directions. The spatial Markov chain can be constructed by l + 1 one-dimensional Markov chains together, but these one-dimensional chains are forced to move to the same location with equal states under the full independence assumption. Then, the conditional probabilities in Eq. (3) can be expressed as

$${ \Pr }(f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} ) = \frac{{p_{{f_{s - 1} f_{s} }} p_{{f_{{s_{1} }} f_{s} }}^{1} \ldots p_{{f_{{s_{l} }} f_{s} }}^{l} }}{{\sum\nolimits_{{f_{s} }} {p_{{f_{s - 1} f_{s} }} p_{{f_{{s_{1} }} f_{s} }}^{1} \ldots p_{{f_{{s_{l} }} f_{s} }}^{l} } }}$$
(4)

where \(p_{{f_{{s_{r} }} f_{s} }}^{r}\) denotes a transition probability in the rth direction from state \(f_{{s_{r} }}\) to \(f_{s}\) and \(p_{{f_{s - 1} f_{s} }}\) denotes a transition probability along moving direction of the spatial Markov chain from state \(f_{s - 1}\) to \(f_{s}\). We can derive the conditional probabilities of two-dimensional Markov chain model (Elfeki and Dekking 2001) and three-dimensional Markov chain model (Li et al. 2012) from Eq. (4). Using the conditional independence assumption, Li (2007) gives the general expression of the conditional probability formula in Eq. (3) at any location s as

$${ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} } \right) = \frac{{p_{{f_{s - 1} f_{s} }} p_{{f_{s} f_{s1} }}^{1} \ldots p_{{f_{s} f_{{s_{l} }} }}^{l} }}{{\sum\nolimits_{{f_{s} }} {p_{{f_{s - 1} f_{s} }} p_{{f_{s} f_{s1} }}^{1} \ldots p_{{f_{s} f_{{s_{l} }} }}^{l} } }}$$
(5)

where \(p_{{f_{s} f_{{s_{r} }} }}^{r}\) denotes a transition probability in the rth direction from state \(f_{s}\) to \(f_{{s_{r} }}\) and \(p_{{f_{s - 1} f_{s} }}\) denotes a transition probability along moving direction of the spatial Markov chain from state \(f_{s - 1}\) to \(f_{s}\).

Generally speaking, the difference between spatial Markov chain model and Markov mesh model is that the latter uses directly the local conditional probabilities in Eq. (3) or the joint probability in Eq. (2), and spatial Markov chain models use multiple one-dimensional transition probabilities or simplified formulas of the local conditional probabilities in Eq. (3). A spatial Markov chain model may be viewed as a special case of Markov mesh models, whereas a Markov mesh model is an extension of spatial Markov chain models, called a generalized spatial Markov chain model.

Spatial hidden Markov chain model

A spatial hidden Markov chain (SHMC), a combination of SMC and hidden Markov model (HMM), is a double random sequence process consisting of a Markov chain and a spatial stochastic sequence. It can make good use of information from well data and auxiliary data. The SHMC is an extension of SMC. It is better able to capture interclass dependency relationships (neighboring relationships, cross-correlations, directional asymmetries) among hidden variables. A spatial Markov chain \(F = \left\{ {F_{1} ,F_{2} , \ldots ,F_{n} } \right\}\) of reservoir categorical variables is characterized by its states and conditional probabilities through Eqs. (4) or (5), and the model is particularly useful as a prior model. The states of the chain except the wells are unobservable, therefore “hidden.” A stochastic sequence \(W = \left( {W_{1} ,W_{2} , \ldots ,W_{n} } \right)\) of reservoir categorical variables is from auxiliary data, and its observed values are denoted by \(w = (w_{1} ,w_{2} , \ldots ,w_{n} )\).

Definition based on Bayes theory

A spatial hidden Markov model uses the posterior probability distribution for modeling reservoir categorical variables and the distribution of the possible states F. Given the observations w, the posterior probability is computed by using the following formula

$${ \Pr }(f|w) = \frac{{{ \Pr }(w|f){ \Pr }(f)}}{{\sum\nolimits_{f} {{ \Pr }(w|f){ \Pr }(f)} }}$$
(6)

Using Eq. (6), the local conditional probabilities are written as

$${ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} ,w_{s} } \right) = \frac{{{ \Pr }(w_{s} |f_{s} ){ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} } \right)}}{{\sum\nolimits_{{f_{s} }} {{ \Pr }\left( {w_{s} |f_{s} } \right){ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} } \right)} }}$$
(7)

where \({ \Pr }(f)\) is the prior probability, which is estimated from well data; \({ \Pr }(w|f)\) is conditional probabilities of the observations w for f fixed, i.e., a likelihood item; \({ \Pr }(w) = \sum\nolimits_{f} {{ \Pr }(w|f){ \Pr }(f)}\) is the probability of W, which is a normalization constant when w is given. We call unobservable f “true states” and w “observed values.” The right side of Eqs. (6) or (7) has been widely used since Thomas Bayes (1764) and Pierre–Simon Laplace (1774) introduced Bayesian statistics, but it is not found in petroleum reservoir hidden Markov application. To simulate reservoir categorical variables using \({ \Pr }(f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} ,w_{s} )\), we need to estimate the conditional probability \({ \Pr }\left( {w_{s} |f_{s} } \right)\) and compute the local conditional probability \({ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} } \right)\) in the right of Eq. (7).

Specifying the prior conditional probability

We use Eq. (8) to define the prior conditional probabilities; the formula is given as follows

$${ \Pr }\left( {f_{s} |f_{s - 1} ,f_{{s_{1} }} , \ldots ,f_{{s_{l} }} } \right) = \frac{{p_{{f_{s - 1} f_{s} }} p_{{f_{s} f_{{s_{1} }} }}^{\left( 1 \right)} \ldots p_{{f_{s} f_{{s_{l} }} }}^{\left( l \right)} }}{{\sum\nolimits_{{f_{s} }} {p_{{f_{s - 1} f_{s} }} p_{{f_{s} f_{{s_{1} }} }}^{\left( 1 \right)} \ldots p_{{f_{s} f_{{s_{l} }} }}^{\left( l \right)} } }}$$
(8)

where \(s_{1} ,s_{2} , \ldots ,s_{l}\) is its nearest known locations of current cell s in different directions; s − 1 is always the start cell of the Markov chain to the unknown cell s, which is to be estimated; the superscript \((1),(2), \ldots ,(l)\) indicates the different lag h.

Thus, we have redefined SMC illustrated in Fig. 1. The prior conditional probabilities can be computed with Eq. (8), where \(\mathop {p_{{f_{s} f_{{s_{l} }} }} }\limits^{(l)}\) is given in transition probability function. Obtaining the local conditional probabilities requires to calculate \({ \Pr }(w_{s} |f_{s} )\). The state value \(f_{s}\) is the “true value” and unobservable except the well data, and the state value \(w\) is regarded as “observation value.” It is noted that \({ \Pr }(w_{s} |f_{s} )\) is essentially the likelihood or the forward model relating facies to sonic impedance; it is not the prior geologic concept, though of course the geology helps to pick the right rock physics and seismic model to relate facies to impedance.

Fig. 1
figure 1

SMC defined by first-order 3-D neighborhood with different lag, cell s is to be studied

Full size image

Case study

Data set

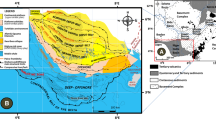
The data we used for our research are gathered from Tahe area of the Tarim Basin in Xinjiang Uygur Autonomous Region, China. Tahe oil field, located in Xayar uplift, north of Tarim basin (Fig. 2), up to now is one of the greatest domestic discoveries in the Paleozoic carbonate rock series. There are two extensive unconformities developed in this area. The Carboniferous clastic rocks directly overlie on the carbonate rocks of Ordovician and underlie the Permian pyroclastic rocks or Triassic formation (Fig. 3). In view of achievements in the carbonate formation of Ordovician, as the seal of it, the Carboniferous (T50–T56), which belongs to the same petroleum system as Ordovician, also shows its exploration potential of lithological reservoir. The purpose layer is located at the depth between 5200 and 5300 m, developed as part of the second formation of the lower Carboniferous (Kalashayi formation). There are three major lithofacies in this work area: mudstone, sandstone and conglomerate. The conglomerate is relatively low in content. We have got four wells’ log data with 509 samples in the three-dimensional space, just as shown in Fig. 4. Three wells are located in the corners of this work area; another well is located inside. The distance in east–west direction of the two wells is 900 and 1200 m in south–north direction, the simulated space is split into a \(30 \times 40 \times 50\) grid system, and each cell is a \(30\;{\text{m}} \times 30\;{\text{m}} \times 2\;{\text{m}}\) cuboid.

Fig. 2
figure 2

Location map of the studied area

Full size image
Fig. 3
figure 3

Stratigraphic chart of Tahe area

Full size image
Fig. 4
figure 4

3-D work area with four wells, x axis and y axis indicate east–west direction and south–north direction, respectively. z axis indicates vertical direction

Full size image

Impedance partition

Figure 5 illustrates some basic descriptive statistics of sonic impedance, such as sample size, mean, variance. The impedance will be regarded as observed value w and will be divided into two classes: strong and weak. By analyzing log and core data, we choose the impedance median 8315.48 as the threshold. The impedance is regarded as strong if it is greater than 8315.48 and weak when it is less than the threshold. By doing so, we derive the emission matrix (Table 1) and the emission probability (Table 2). The initial proportion of each reservoir categorical variable can be computed from Table 1. Mudstone is 62.87 %, sandstone is 31.24 %, and conglomerate is 5.89 %, respectively. The impedance of each class is depicted in Fig. 6. By analyzing Table 2 and Fig. 6, we may find that the impedance of mudstone tends to be stronger than sandstone and conglomerate.

Fig. 5
figure 5

Basic descriptive statistics of sonic impedance, blue curve is the cumulative distribution function

Full size image
Table 1 Emission matrix
Full size table
Table 2 Emission probability
Full size table
Fig. 6
figure 6

Impedance of each reservoir categorical variable. Conglomerate: left, sandstone: middle, mudstone: right

Full size image

Transiogram models

The magnitude of the transition probability depends on a sampling interval, i.e., the transition probability is a nonlinear function of the sampling intervals (Carle and Fogg 1997). By increasing sampling interval, the transition probability forms a transition probability function (also called “transiogram”), which is regarded as a measure of spatial continuity (Li 2006). Experimental transiograms are estimated from the 509 points and fitted by exponential models. The fitted transiogram models are used for simulations. Because raster data are used, the lag h represents as the number of pixels (i.e., grid units), not the exact distance. Figure 7 illustrates the experimental auto-/cross-transiograms and their fitting models. It can be seen that most of these experimental transiograms can be approximately fitted by an exponential model. We also find that some experimental transiograms have apparent fluctuations that are difficult to fit using the basic model, such as \(p_{22} \;{\text{and}}\;p_{23}\). This may be caused by the insufficiency of observed data and the non-Markovian effect of the real data. Fitted transiogram models capture only part of the features of experimental transiograms, depending on the complexity of the mathematical models used (Li 2007). Using composite hole-effect models (Ma and Jones 2001) may capture more details, such as periodicities, of experimental transiograms.

Fig. 7
figure 7

Experimental transiograms and fitted models

Full size image

Simulation results

The SHMC can be determined by initial probabilities (prior probabilities) C, transition matrix A and emission matrix B. The states sequence depends on C and A, while the observed sequence is determined by B. As a result, the SHMC can be expressed as \(\lambda = \left( {A,B,C} \right)\). We consider a first-order neighborhood, which contains six neighbors in 3-D space. Transition matrix A can be computed by Eq. (8), where l = 6. By using the transition probabilities from Fig. 7, the final result of transition matrix A with lag \(h = 1,2,3 \ldots ,l\) is

$$A = \left( {\begin{array}{*{20}c} { 0. 7 9 5 2} & { 0. 2 0 1 1} & { 0. 0 0 3 7} \\ { 0. 2 5 3 4} & { 0. 6 9 6 7} & { 0. 0 4 9 9} \\ { 0. 1 2 7 1} & { 0. 0 6 0 8} & { 0. 8 1 2 1} \\ \end{array} } \right)$$

where the main diagonal elements indicate the probabilities transfer between same reservoir categorical variables; 0.2011, for example, is the probability transfer from mudstone to sandstone. Emission matrix B is

$$B = \left( {\begin{array}{*{20}l} { 0. 6 9 3 8} \hfill & { 0. 3 0 6 3} \hfill \\ { 0. 1 7 6 1} \hfill & { 0. 8 2 3 9 { }} \hfill \\ { 0. 1 6 6 7} \hfill & { 0. 8 3 3 3} \hfill \\ \end{array} } \right)$$

which is given in Table 2. Initial probabilities (prior probabilities) C are

$$C = \left( {\begin{array}{*{20}c} {0.6287} & {0.3124} & {0.0589} \\ \end{array} } \right)^{T} .$$

By using Viterbi algorithm, four realizations are simulated for work area (Fig. 8). In order to compute the simulation accuracy of the SHMC method, another well, S75, is added in the middle of the section between wells 66 and 67 (Fig. 9). Note that “S75” is a short notation for “well 75.” We have got 121 lithofacies samples in this well. The newly obtained log data can be used as validation sets. By comparing the estimated lithofacies in S75 location with the true facies, we obtain the classification accuracy, which can be defined as

$${\text{Accuracy}} = \frac{{\# {\text{correct}}\;{\text{classification}}}}{{\# {\text{validation}}\;{\text{sets}}}}.$$
Fig. 8
figure 8

Four realizations implemented by SHMC. Mudstone: red, sandstone: yellow, conglomerate: blue

Full size image
Fig. 9
figure 9

A section to be simulated across three wells

Full size image

The average prediction accuracy is 63.64 % according to four stochastic simulation results (Table 3).

Table 3 SHMC classification accuracy
Full size table

Comparison analysis

To better demonstrate the superiority of the SHMC method, a comparison study has also been conducted. We partition this area into a 100 × 200 grid system, with each unit denoting a 1 m × 4.5 m subsection (Liang 2014). At first, there is no auxiliary information for integration. Thus, we use SMC defined by Eq. (8) for estimation of petroleum reservoir categorical variables. The simulation results obtained by three conditional wells have been shown in Fig. 10. It is obvious that conditional data have played a role in controlling the distribution of lithofacies near the wells. However, the further counterparts are fragmented and random in the grid. The average prediction accuracy is 59.50 % according to four stochastic simulation results (Table 4).

Fig. 10
figure 10

Four stochastic simulation results based on three wells

Full size image
Table 4 Classification accuracy comparison
Full size table

For comparison, the SHMC method has been applied by adding seismic data. Through stratum calibration, time–depth conversion, as well as wave impedance inversion, a seismic section across three wells can be obtained (Fig. 11). Using the impedance partition criterion, we can compute the emission matrix B. The entries in this matrix are \({ \Pr }(w_{s} |f_{s} )\), which can be used in Eq. (7) to calculate the posterior conditional probability combining with Eq. (8). Simulation results have been shown in Fig. 12. The average prediction accuracy increases up to 64.46 % according to four stochastic simulation results (Table 4). Unlike Fig. 10, lithofacies distribution displays certain patterns in random results. More specifically, the distribution of sandstone is not continuous as a whole, with extension about 400–500 m in the horizontal direction. In addition, the section can be divided into three small layers from top to bottom. The middle layer, with the thickness of around 20 m, is twice as thick as the upper and lower ones. Each layer is stacked in space, not connected with each other. As the background lithofacies, mudstone exists widely in this area. Conglomerate, on the other hand, is not well developed due to petroleum geology condition. The simulation results and wave impedance inversion results have good correspondence, which demonstrates that the SHMC model is preferred in the estimation of petroleum reservoir categorical variables.

Fig. 11
figure 11

A seismic section across three wells

Full size image
Fig. 12
figure 12

Four stochastic simulation results based on three wells and sonic impedance

Full size image

Conclusions

We have presented an SHMC model for geological facies modeling. This combines spatial Markov chain theory and Bayes estimation. We have adopted the specification of earlier published hidden Markov models. SHMC is based on neighborhood and cliques and has a solid theoretical foundation. Unlike SMC, SHMC integrates well data and geological conceptual data (sonic impedance) by using Viterbi algorithm. In our research, the sonic impedance is divided into two classes: strong and weak, which is regarded as observed variable. Experimental transiograms and fitted models are given according to 509 samples, which are used to compute prior conditional probabilities (transition probabilities). Compared with SMC based on well data, the SHMC method performs superiority both in prediction accuracy and reflecting the geological sedimentation process by integrating auxiliary information.