Introduction

Multi-phase flow in porous media is an important issue in its applications including oil and gas production, enhanced oil recovery (EOR), and gas storage techniques (Cao and Siddiqui 2011). One of the key petrophysical parameters to characterize the hydrodynamics of multiphase flow in porous media is relative permeability. Relative permeability can provide useful information for reservoir characterization, reservoir simulation, reservoir recovery calculation, and formation damage (Dake 1978; Honarpour et al. 1986; Honarpour and Mahmood 1988). Unfortunately, it still remains tough to obtain three-phase relative permeability data directly from the field, any indirect manner, or experiments. It becomes very important to obtain individual two-phase relative permeability of three phase system from appropriate experimental design and numerical construction.

The laboratory methods used to calculate relative permeability functions are grouped into centrifuge, steady- and unsteady-state techniques. The centrifuge method has limitations including loss of information on low saturation region that cannot be gained from the production data as low mobility ratio (Hirasaki et al. 1995). A simplified analysis of centrifuge method could miss some significant information of actual relative permeability. Steady-state methods have some disadvantages, especially in low permeability rocks where it is laborious to reach multiple steady states, and capillary forces and capillary end effects are significant (Kamath et al. 1993; Schembre and Kovscek 2003). Steady-state techniques have been improved by correcting capillary effects, but they still require successive measurements for different total flow rates and steady-state condition confirmations (Virnovsky et al. 1995). Capillary pressure has a significant effect on saturation distribution and recovery, and capillary forces dominate multiphase flow in low permeability rocks and fractured reservoirs. Unsteady-state method still remained widely utilized to estimate relative permeabilities. In developing unsteady-state methods for low-permeability systems, it is necessary to account for capillary pressure when obtaining the relative permeability curve. Akin and Kovscek (1999) showed that the use of the (unsteady) JBN technique leads to inaccurate assessment of relative permeability in some cases.

Both explicit and implicit approaches in literatures are well documented for interpreting unsteady-state dynamic displacement experiment. Johnson et al. (1959) and Jones and Roszelle (1978) methods are explicit interpretive methods. Relative permeability values are computed directly from dynamic displacement data. However, these methods have two primary limits as follows: (a) analysis are limited to Buckley–Leverett model extended by Welge (1952) and not appropriate for low-flow rate experiments with significant effect of capillary pressure; (b) these methods require numerical or graphical differentiation of experimental data (Blair and weinaug 1969). The other implicit method was developed to overstep the limitations that are associated with the explicit approach. Relative permeability curves are computed by representing them by two functions, each of which contains certain coefficient that controls the shape accuracy of the relative permeability curves. After determination of saturation and relative permeability end point values, relative permeability curvatures in mathematical function can be adjusted until the flow behavior match the laboratory observations. Therefore, an automatic history match like method could be developed to optimize curvatures (Sigmund and McCaffery 1979; Kerig and Watson 1987; Bech et al. 2000; Toth et al. 2001; Jaber 2013). For these relevant references, the determination of relative permeability curves is executed by representing it with two functions, each of which contains one coefficient to be adjusted to match the observations. The values of these coefficients are calculated for different rocks by employing nonlinear-least-squares optimization procedure.

In this study, oil–water based core-flooding system was designed and used to conduct the two-phase dynamic displacement experiment. This system could be used to obtain the pressure drop and production data automatically from dynamic displacement in reservoir condition. In addition, estimation of relative permeability curves from two-phase displacement experiments was considered. This is achieved through preparing a relative-permeability calculation program (RCP) by which relative permeability curves could be determined. Employing numerical techniques solves the mathematical models, which are used to develop the RCP program. The implicit method is used for this purpose.

Dynamic displacement experiment

Core-flooding system design

In dynamic displacement experiment, breakthrough time and fluid outflow performance are key parameters to calibrate the real time production profile and have to be identified carefully. In traditional measurement, breakthrough time is usually determined by pressure-difference data because we cannot see the production of first-oil or first-water in displacement experiment. It becomes a tough work while utilizing a heterogeneous core sample resulted in complex pressure-drop data. In the same way, fluid outflow performance is measured through burette as usual and always causes inaccurate result with low injection rate.

Two components are designed and added on core-flooding system presented in this study to improve above problems. One is two-phase detector probe which is connected to outflow endcap of core holder. This component will show the record on time while phase change in flow line. Detail function of detector probe is presented in Appendix 1. Limit dead volume of 0.14 ml from endcap to probe is small enough to cause a precise determination of breakthrough time. The other one is acoustic separator equipped with an ultrasonic transducer for detection of liquid–liquid interfaces. Similar to the separator design in core-flooding experiment references (Maloney 1993; Maloney and Dogett 1995), the separator in this study was employed ultrasonic level monitor technique to detect the oil–water meniscus after breakthrough of core-flooding experiment. The production volume of target fluid (oil in this study) could be determined through oil–water level movement detected by sound reflection technique (please see Appendix 1 for more detail). The relative proportion of effluent is sensed by a sound reflection technique that utilizes an acoustic pulse triggered at the bottom of the measurement bore. The pulse travels upward through the denser fluid occupying the lower section and is reflected by the fluid interface. The fluid volume is determined by the comparison of the travel time of the reflected pulse from the fluid interface and the simultaneous reflected pulse from a target at a known height thus performing a continuous calibration allowing the system to determine precise volumes even in varying density situations such as temperature and pressure variation and small time interval.

An unsteady-state core-flooding system was designed in Fig. 1 for oil–water dynamic displacement experiments. The parts within the oven were: pre-heating tube to enable injected fluid in desired temperature, thermal couple to detect the inlet and outlet fluid temperature, pressure transducer to detect the pressure drop, and core holder to install the tested core sample. The core holder with horizontal orientation accommodates cores 1.5 in. in diameter, up to 4 in. long. The core holder is a “Hassler Sleeve” type core holder which allows the core samples to be inserted without disassembling the holder. The confining pressure was provided from air-driven pneumatic pump. Wetting and non-wetting phases were initially filled within individual syringe pump, and injected with constant flow model in designed rate. Both inlet and outlet flow lines were designed with minimum volume to decrease the dead volume effect which delay the breakthrough in real time and makes non-simultaneous response with pressure drop (Appendix 1 shows improvement using detector probe).

Fig. 1
figure 1

Schematic diagram of unsteady-state core-flooding system

Full size image

Pressure drop data from the dynamic displacement experiment were measured using a Validyne DP15TL variable-reluctance DPT with a CD12 carrier demodulator to produce a 0–10 V DC signal. Production data were measured with acoustic separator with purpose to allow two fluids of different density to be separated and relative volumes of these fluids to be measured. An acoustic transducer is mounted in the base of the measurement cylinder, and it is excited with a voltage causing it to emit a high frequency ultrasonic wave in the fluid. These ultrasonic waves could be easy to determine the outflow fluids ratio and each volume on time.

The back pressure regulator is dome-loaded back pressure regulator controlled by a flexible diaphragm with pilot pressure acting on the back side of the diaphragm. Pilot pressure on the back of the diaphragm is generated by an air-driven, high pressure pump. The back pressure regulator could allow reservoir pressure condition up to 5000 psi.

Experimental procedure

Two in situ core plug samples with 1.5 in. diameter and 2.4 in. long were cleaned by flow-through method with Lab solvent to strongly water wet stage. After core cleaning, these samples were dried for 24 h at 80 °C and carried on to routine core analysis with porosity and permeability. Then special core analyses of capillary pressure were then conducted before dynamic displacement tests. The core samples were then saturated with formation synthetic brine, followed by a crude-oil flood to simulate the inflow of oil into the core. The cores were then aged at the reservoir temperature for 30 days to establish adsorption equilibrium to restore wettability.

After restoring native wettability, diesel-3 wt % brine flood tests in core samples were used to obtain the needed data (pressure drop and production of pore fluid) for further relative permeability analysis. In this study, the density difference of 0.26 g/ml (0.817 g/ml of diesel and 1.085 g/ml of brine) of test fluids was found to be separated by acoustic separator easily. Initially, diesel was injected about 100 pore volumes (PV) to replace the crude-oil, following first imbibition and drainage process with 0.5 ml/min injection rate and 100 PV injection were conducted to investigate the minimum and maximum water saturation in core plug sample. In final stage, brine was then injected to displace the diesel with 0.5 ml/min flow rate in 25 °C and ambient pressure condition. The displacement experiments were terminated after ~99.9 % water-cuts or 100 movable PV brine injected. In this study, we just conducted imbibition displacement experiment for field EOR purposes. Drainage displacement experiment would be performed through reference data and analyzed through RCP as following section.

Relative-permeability Calculation Program (RCP)

Mathematical formulation

The X-shape relative permeability curves descripted two-phase flow are to be computed by assuming a function of two parameters, then use is made of optimization technique to calculate the optimum value. An objective function is constructed as a weighted sum of squared differences between the measured and the calculated data from a mathematical model of core-flooding experiment. The objective function can be determined as follows:

$$\Phi = \sum\limits_{i = 1}^{ni} {W_{Pi} } \left( {\Delta P^{\text{obs}} - \Delta P^{\text{cal}} } \right)^{2} + \sum\limits_{j = 1}^{nj} {W_{Qj} } \left( {Q_{P}^{\text{obs}} - Q_{P}^{\text{cal}} } \right)^{2}$$
(1)

where \(\Phi\) is the objective function, \(\Delta P^{\text{obs}}\) and \(Q_{P}^{\text{obs}}\) are observed pressure drop and pore fluid production, \(\Delta P^{\text{cal}}\) and \(Q_{P}^{\text{cal}}\) are calculated pressure drop and pore fluid production, \(W_{\text{Pi}}\) and \(W_{\text{Qj}}\) are weighting factors for pressure and production items. Two mathematical models have been considered; one for imbibition process and the other for drainage process. The quantities, \(\Delta P^{\text{cal}}\), and \(Q_{P}^{\text{cal}}\) may be obtained by solving these models.

In Eq. (1), measurement errors are assumed to be uncorrelated because sufficient information is rarely available to do otherwise. Maximum-likelihood/minimum-variance estimation of the parameters can be calculated by using variances inversions of measurement errors. The variance of a quantity n is defined as follows:

$$\sigma_{n}^{2} = E\{ [n - E(n)]^{2} \}$$
(2)

where E is the expected value operator. The Maximum-likelihood weighting factor can be rewritten as follows.

$$W_{\text{Pi}} = 1/\sigma_{\text{pi}}^{2} \,\;\;{\text{and}}\;\;W_{\text{Qj}} = 1/\sigma_{\text{Qj}}^{2}$$
(3)

The weights used in the procedure were 1.0 for all the recovery data, 0.1 for pressure drop data made before breakthrough, and 1.0 thereafter. The choice of this weighting scheme partly reflected the spacing of data and also the belief that early pressure data were somewhat less reliable than data obtained after breakthrough.

Because the variances of the measurement errors are unknown, estimates of those quantities are to be used. The quantities \(\Delta P^{\text{cal}}\) and \(Q_{P}^{\text{cal}}\) are obtained from imbibition and drainage model. It means that the mathematical model to be used must adequately describe the experiment if unbiased maximum-likelihood estimates are to be obtained. Then, the relative permeability curves can be specified by functional form containing adjustable parameters.

The determination of adjustable parameters is a nonlinear minimization problem. The process of minimizing the objective function is starting with initial guess and generating subsequent parameter estimates that yield smaller values of the objective function. The iterative process can be continued until a suitably small objective function or no further improvements can be determined. It means model has to set the absolute function tolerance, scaled gradient tolerance and step tolerance of distance between two guesses. The optimization process will stop while satisfying the absolute function tolerance, scaled gradient tolerance and step tolerance in turn.

Functional relative permeability curves

The relative permeability curves for both wetting and non-wetting phases may be written as follows.

$$k_{\text{rw}} = k_{\text{rw}}^{0} \left( {\frac{{S_{\text{e}}^{{\varepsilon_{\text{w}} }} + AS_{\text{e}} }}{1 + A}} \right)$$
(4)
$$k_{\text{rnw}} = k_{\text{rnw}}^{0} \left( {\frac{{(1 - S_{\text{e}} )^{{\varepsilon_{\text{nw}} }} + B(1 - S_{\text{e}} )}}{1 + B}} \right)$$
(5)
$$S_{\text{e}} = \frac{{S_{\text{w}} - S_{\text{wmin}} }}{{S_{\text{wmax}} - S_{\text{wmin}} }}$$
(6)

where A and B are constants to be suggested to be 0.01 for computational purpose to linearize the relative permeability curves as these curves approach zero, but which otherwise do not influence the shapes of curves; \(S_{\text{e}}\) is effective water saturation; \(S_{\text{w}}\) is water saturation; \(S_{\text{wmax}}\) and \(S_{\text{wmin}}\) are maximum and minimum values of water saturation for first imbibition and drainage displacement test; \(k_{\text{rw}}\) is wetting phase relative permeability; \(k_{\text{rnw}}\) is non-wetting phase relative permeability; \(k_{\text{rw}}^{0}\) is endpoint relative permeability value of wetting phase; \(k_{\text{rnw}}^{0}\) is endpoint relative permeability value of non-wetting phase; \(\varepsilon_{\text{w}}\) and \(\varepsilon_{\text{nw}}\) are power law constant of curves, these two values are chosen to minimize Eq. (1) by employing Gauss–Newton with Levenerg–Marquardt modification procedure.

The Levenberg–Marquardt algorithm (LMA) known as the damped least-squares method is used to solve non-linear least squares problems in this study. The LMA interpolates between the Gauss–Newton algorithm (GNA) and the method of gradient descent. GNA is known to have stability issues, especially when the starting point is far from the solution point. Levenberg modified the Gauss–Newton algorithm and added a gradient descent term to assist with convergence. Marquardt modified the Levenberg equation by replacing the identity term with the diagonal of the Jacobian trasponse times the Jacobian, which created the LMA to improve the rate of convergence when compared to the Levenberg algorithm.

$$(J^{T} J + \mu {\text{diag}}(J^{T} J))(P_{1} - P_{0} ) = J^{T} E_{P0}$$
(7)

where \(J\) is the vector of objective function to be minimized; \(\mu\) is Marquardt number; \(P_{0}\) and \(P_{1}\) are vectors of adjusted values before and after optimization step. The Levenberg–Marquardt algorithm works by starting with an initial guess of the adjustable parameters used as \(P_{0}\). The residual error and the Jacobian are then solved from Eq. (1). Equation (7) is then used to solve for \(P_{1}\). The residual error is computed at this new \(P_{1}\)  . If the new residual error is greater than the original residual error, then the new \(P_{1}\) is rejected, \(\mu\) is increased, and a new \(P_{1}\) is calculated. If the new residual error is less than the starting residual error, then the new \(P_{1}\) values are accepted and \(\mu\) is decreased. The new accepted \(P_{1}\) becomes the new \(P_{0}\) and the algorithm is repeated until it either converges or goes unstable.

Solving a nonlinear least squares problem for relative permeability curve power law constant can be subjected to bounds on the variables using LMA algorithm. In Fortran language, Math library (IMSL database) support the built-in optimization sub-program BCLSF for finite-difference Jacobian, or BCLSJ for user-supplied Jacobian. For more popular Matlab language, the math tool box also has the built-in optimization sub-program LSQCURVEFIT and LSQNONLIN. The User familiar to different program language could utilize the built-in optimization sub-program to generate the code efficiently.

The endpoint relative permeabilities can be determined by experimental measurements as follows.

$${\text{Imbibition:}}\;k_{\text{rnw}}^{0} = {\raise0.7ex\hbox{${Q_{i} L\mu_{\text{w}} }$} \!\mathord{\left/ {\vphantom {{Q_{i} L\mu_{\text{w}} } {kA(\Delta P_{\text{nw}} )_{\text{init}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${kA(\Delta P_{\text{nw}} )_{\text{init}} }$}}$$
(8)
$$k_{\text{rw}}^{0} = {\raise0.7ex\hbox{${(\Delta P_{\text{nw}} )_{\text{init}} \mu_{\text{w}} k_{\text{rnw}}^{0} }$} \!\mathord{\left/ {\vphantom {{(\Delta P_{\text{nw}} )_{\text{init}} \mu_{\text{w}} k_{\text{rnw}}^{0} } {\mu_{\text{nw}} (\Delta P_{\text{nw}} )_{\text{final}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{\text{nw}} (\Delta P_{\text{nw}} )_{\text{final}} }$}}$$
(9)
$${\text{Drainage:}}\;k_{\text{rw}}^{0} = {\raise0.7ex\hbox{${Q_{i} L\mu_{\text{w}} }$} \!\mathord{\left/ {\vphantom {{Q_{i} L\mu_{\text{w}} } {kA(\Delta P_{\text{nw}} )_{\text{init}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${kA(\Delta P_{\text{nw}} )_{\text{init}} }$}}$$
(10)
$$k_{\text{rnw}}^{0} = {\raise0.7ex\hbox{${(\Delta P_{\text{nw}} )_{\text{init}} \mu_{\text{nw}} k_{\text{rw}}^{0} }$} \!\mathord{\left/ {\vphantom {{(\Delta P_{\text{nw}} )_{\text{init}} \mu_{\text{nw}} k_{\text{rw}}^{0} } {\mu_{\text{w}} (\Delta P_{\text{nw}} )_{\text{final}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{\text{w}} (\Delta P_{\text{nw}} )_{\text{final}} }$}}$$
(11)

where \(Q_{i}\) is injection rate, cm3/s; \(L\) is core length, cm; \(\mu_{\text{w}}\) and \(\mu_{\text{nw}}\) are wetting and non-wetting phase viscosities, cp; \(k\) absolute permeability, mD; \(A\) cross section area of core sample, cm2; \((\Delta P_{\text{nw}} )_{\text{init}}\) non-wetting phase initial pressure; \((\Delta P_{\text{nw}} )_{\text{final}}\) non-wetting phase final pressure. The values of \(k_{rw}^{0}\) and \(k_{\text{rnw}}^{0}\) are considered as constants in the model calculations. The endpoint relative permeabilities can also be subjected to optimization process. Validation of Eqs. (8)–(11) were confirmed in numerical study but not presented here.

Imbibition and drainage models

The flow equations for unsteady state displacement of incompressible, one-dimensional, two phases fluid flow (which include capillary pressure and ignore gravity effects) may be expressed as follows (Aziz and Settari 1979).

$$\frac{k}{{\mu_{\text{w}} }}\frac{\partial }{\partial x}\left[ {k_{\text{rw}} \frac{{\partial P_{\text{w}} }}{\partial x}} \right] = \phi \frac{{\partial S_{\text{w}} }}{\partial t} + q_{\text{wi}}$$
(12)
$$\frac{k}{{\mu_{\text{nw}} }}\frac{\partial }{\partial x}\left[ {k_{\text{rnw}} \frac{{\partial P_{\text{nw}} }}{\partial x}} \right] = \phi \frac{{\partial S_{\text{nw}} }}{\partial t} + q_{\text{nwi}} = - \phi \frac{{\partial S_{\text{w}} }}{\partial t} + q_{\text{nwi}}$$
(13)
$$S_{\text{w}} + S_{\text{nw}} = 1$$
(14)
$$P_{\text{c}} = P_{\text{nw}} - P_{\text{w}}$$
(15)

where \(P_{\text{w}}\) is wetting phase pressure; \(S_{\text{w}}\) is wetting phase saturation; \(q_{\text{wi}}\) is wetting phase injection rate; \(P_{\text{nw}}\) is non-wetting phase pressure; \(S_{\text{nw}}\) is non-wetting phase saturation; \(q_{\text{nwi}}\) is non-wetting phase injection rate; \(\phi\) is porosity; \(P_{\text{c}}\) is capillary pressure and can be expressed as follows.

$$P_{\text{c}} = P_{\text{cb}} \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {(S_{\text{pc}} )^{1/\lambda } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(S_{\text{pc}} )^{1/\lambda } }$}} - 1} \right)$$
(16)
$$S_{\text{pc}} = \frac{{S_{\text{w}} - S_{\text{wirr}} }}{{S_{\text{wo}} - S_{\text{wirr}} }}$$
(17)

where \(P_{\text{cb}}\) is scaling factor consisted of interfacial tension and mean pore size similar to group \(\sigma /\sqrt {k/\phi }\); \(S_{\text{pc}}\) is effective saturation in capillary pressure; \(\lambda\) is curve shape factor; \(S_{\text{wirr}}\) is irreducible water situation; \(S_{\text{wo}}\) zero capillary pressure saturation.

The methods of solution used for treating the nonlinear terms of Eqs. (12)–(15) are descripted as following three main steps: (a) one-point upstream transmissibility weighting; (b) fully implicit transmissibilities using chord slope method to estimate derivatives; (c) Newton’s–Raphson’s method to handle nonlinearities resulting from the use of capillary pressure. The boundary and initial conditions for Eqs. (12)–(15) are well descripted by Aziz and Settari (1979) and Sigmuned and McCaffery (1979), and would not be presented in the study.

Evaluation of RCP program

For comparison with different size core sample in the same scale, the dimensionless cumulative injection \(Q_{\text{PV}}\), the recovery response \(E_{\text{R}}\), and the dimensionless pressure response \(\Delta P_{\text{D}}\) for both the imbibition and drainage cases are required to be determined.

$$Q_{\text{PV}} = {\raise0.7ex\hbox{${tQ_{i} }$} \!\mathord{\left/ {\vphantom {{tQ_{i} } {\phi AL(S_{\text{wmax}} - S_{\text{wmin}} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\phi AL(S_{\text{wmax}} - S_{\text{wmin}} )}$}}$$
(18)
$$E_{\text{R}} = \left( {{\raise0.7ex\hbox{${\overline{{S_{\text{w}} }} - S_{\text{wmin}} }$} /\hbox{${S_{\text{wmax}} - S_{\text{wmax}} }$}}} \right) \times 100$$
(19)
$$\Delta P_{\text{D}} = \left({P}_{\text{nw}} (0,t) - P_{\text{nw}}(L,t)/P_{\text{nw}} (0,0^{ + } ) - P_{\text{nw}} (L,0^{ + })\right) \times 100$$
(20)

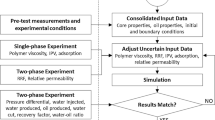
The entire relative permeability analysis procedure was presented in Fig. 2. To validate the RCP program, the experimental data presented by Sigmuned and McCaffery (1979) with Swan Hills core sample were re-analyzed through RCP program and CMG IMEX software. Table 1 and Figs. 3 and 4 show the parameters used and analysis results. The CMG IMEX used the Sigmuned’s inputs including power law parameters (\(\varepsilon_{\text{w}}\) and \(\varepsilon_{\text{nw}}\)) as Table 1 to generate the firm pressure drop and recovery curves in Figs. 3 and 4 which show the observed and simulated dimensionless pressure drop (\(\Delta P_{\text{D}}\)) and recovery response (\(E_{\text{R}}\)) data as functions of the dimensionless cumulative injection, \(Q_{\text{i}}\). The core-flooding experiment parameters were input in RCP program to generate optimized pressure drop and recovery curves in Figs. 3 and 4 and output the values of power law parameters in Table 1. The RCP results show good match with references data and CMG software results. The two parameters relative permeability curves characterized by the values of \(\varepsilon_{\text{w}}\) and \(\varepsilon_{\text{nw}}\) given in Table 1 are shown in Fig. 5 for both the imbibition and the drainage displacements. The validated RCP program could then be utilized to analyze the dynamic displacement experiment data.

Fig. 2
figure 2

The process of RCP program to relative permeability analysis

Full size image
Table 1 Referenced core-flooding experiment inputs and results
Full size table
Fig. 3
figure 3

Imbibition displacement results from reference experiment, CMG calculation, and RCP optimization

Full size image
Fig. 4
figure 4

Drainage displacement results from reference experiment, CMG calculation, and RCP optimization

Full size image
Fig. 5
figure 5

Imbibition and drainage relative permeability curves results from RCP program

Full size image

Displacement experiment responses with mobility ratio

Mobility ratio defined as Eq. (21) would cause a quite different shape at pressure difference responses. Since pressure difference response is very sensitive to injection rate change in small time interval and background values, a selection of experiment fluid with different mobility ratio should be important.

$$M = {\raise0.7ex\hbox{${\mu_{l} k_{rd}^{0} }$} \!\mathord{\left/ {\vphantom {{\mu_{l} k_{rd}^{0} } {\mu_{d} k_{rl}^{0} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\mu_{d} k_{rl}^{0} }$}}$$
(21)

where d and l refer to displacing and displaced phase, respectively; \(k_{rd}^{0}\) and \(k_{rl}^{0}\) are end point values of relative permeability curves. Figure 6 shows imbibition pressure difference and recovery responses from RCP with upper limit of viscous to capillary forces, \(\varepsilon_{\text{w}}\) = 3, and \(\varepsilon_{\text{nw}}\) = 3. The curves shown for M = 1 are typically generated from homogeneous water-wet cores when oil viscosity is less than 1 cp. In such case, pressure response would rise until breakthrough of injection fluid, and little oil production occurs after breakthrough. Both pressure and recovery observations are easy to be extracted from real time log data. The curves shown for M = 2 and 8 are generally displacement experiments conducted from viscous oil in water-wet core samples, or light oil in oil-wet core samples. Pressure difference would raise a little or go down from initial value to be recorded hardly. Fast breakthrough might cause a long recovery period to enlarge the analysis time. Light oil for water-wet core samples and heavy oil for oil-wet core samples would cause both experiment and analysis more effective.

Fig. 6
figure 6

Pressure difference and recovery responses for different mobility ratio

Full size image

Results

Routine core analysis

Two in situ core plug samples taken from West-Africa B block in B basin with depths of 2479 m (A sample) and 2850 m (B sample) were used in core-flooding experiments. These two core plug samples are representative sandstone in their own reservoir. The reservoir conditions for each core sample are 172 °F and 3300 psi for A sample, 206 °F and 3900 psi for B sample. Porosity of the cores was measured using Permeameter-Porosity Meter with helium gas. The CoreLab CMS-300 which is an automated machine capable of measuring values at a range of confining pressures was used to measure the porosity by method called “Boyle’s law Single Cell Method for direct void volume measurement”. Pore volumes were determined by the gas expansion method using Helium. Klinkenberg permeabilities were determined by transient pressure decay technique using helium gas. From these data, the Klinkenberg gas slippage and Forchheimer turbulence factor were calculated. Grain volumes were determined at room conditions in a matrix cup applying the Boyle’s Law gas expansion method. Grain densities were calculated from these data and the dry weights of the samples. Above measurements are summarized in Table 2.

Table 2 Routine core analysis results
Full size table

The samples then were evacuated of air and pressure-saturated with synthetic formation brine in preparation for testing. The brine saturated samples were weighed and placed in individual centrifuge cups. The samples were spun at incremental rotational speeds effecting air displacing brine. The core plugs remained at each capillary pressure until equilibration had been achieved for that pressure for a minimum period of 24 h. Equilibration was identified when the volume of fluid displaced from each core plug remained constant. The volume of brine displaced from each core plug was determined while the rotor was spinning with the use of a stroboscopic light illuminating the receiving tube. Brine displacements were recorded as the samples reached capillary equilibrium at each pressure. At the end of the air–water displacement the samples were removed from the centrifuge and weighed to determine the final fluid volumes. Capillary pressure and saturation data were derived from the volumes of brine displaced, core plug pore volume and corresponding pressures capillary pressure (Pc) was calculated from rates of rotation using the following equation:

$$P_{\text{C}} = 1.578 \times 10^{ - 7} \;(\rho_{\text{b}} - \rho_{\text{air}} )\;(R - L/2)\;L\,{\text{RPM}}^{2}$$
(22)

where \(\rho_{\text{b}}\) is density of brine, g/cm3; \(\rho_{\text{air}}\) is density of air, g/cm3; \(R\) is distance from centre of rotation to outer face of the core plug, cm; L is length of core plug, cm; RPM is revolutions per minute. The average brine saturations were corrected for capillary end effects to end-face brine saturations using a method devised by Pierre Forbes. Inlet-face saturations (S w) of two samples were determined using Forbes methodology are plotted in Fig. 6. The air–brine capillary pressures were then converted to oil–water system by measuring the interfacial tension between diesel and brine, and then subjected to RCP program to calculate relative permeability.

Dynamic displacement experiments

After centrifuge capillary test, those core samples were then saturated with formation synthetic brine, followed by a crude-oil flood to simulate the inflow of oil into the core. The cores were then aged at the reservoir temperature for 30 days to establish adsorption equilibrium to restore wettability. Diesel was then injected about 100 PV of each sample to replace the crude-oil, following first imbibition and drainage process with 0.5 ml/min injection rate and injected 100 PV were conducted to investigate the minimum and maximum water saturation in core plug sample. Effective permeability to oil at immobile water saturation was determined at ambient temperature and net confining pressure. This will be used as the “base permeability” for later relative permeability calculations. Table 3 summarized these pre-handling test results.

Table 3 Brine-oil relative permeability pre-handling measurement
Full size table

After pre-handling test, core sample then moved on to imbibition displacement experiment. The displacement experiments were then conducted at 25 °C and ambient pressure condition. Unsteady-state brine-oil relative permeability test was initiated by flooding brine through the sample at a constant rate with 0.5 ml/min, while the incremental produced volumes of water and oil were collected. The differential pressure together with elapsed time were monitored and recorded. Test was terminated at water-cuts in excess of 99.95 %. Effective permeability to water at residual oil saturation was determined at this point. Each sample was unloaded and weighed, unsteady-state water–oil relative permeability relationships were calculated from the collected data along with sample and fluid parameters using RCP program.

Figure 7 shows the observed dimensionless pressure drop (\(\Delta P_{\text{D}}\)) and recovery response (\(E_{\text{R}}\)) data obtained from the experiments. These data, plotted as open circles and triangles, are given as functions of the dimensionless cumulative injection, \(Q_{\text{i}}\). Figure 7 also shows the simulator calculated values obtained from RCP program. Initial estimates of \(\varepsilon_{\text{w}}\) = 1 and \(\varepsilon_{\text{nw}}\) = 1 were made by comparing the observed data with calculated dimensionless response curves. The weights used in the calculation were 1.0 for all the recovery data, 0.1 for pressure drop observations made before breakthrough, and 1.0 thereafter suggested by Sigmund and McCafery (1979). The choice of this weighting scheme partly reflected the spacing of data and the belief that early pressure data were somewhat less reliable than data obtained after breakthrough. The final simulated values with \(\varepsilon_{\text{w}}\) = 2.29 and \(\varepsilon_{\text{nw}}\) = 3.17 of A sample and \(\varepsilon_{\text{w}}\) = 1.26 and \(\varepsilon_{\text{nw}}\) = 6.38 of B sample show good agreements with experimental data. The curves are thought to resemble typical water–oil imbibition curves for intermediate-wet cores, or for cores with well-distributed heterogeneities descripted by Sigmund and McCafery (1979). Figure 8 shows the oil–brine relative permeability curves of A and B sample from RCP program. Both Samples A and B show a less energy consuming movement for wetting phase, and energy consuming for non-wetting phase. Movement of oil phase would become tough with presence of water phase. It would cause early water breakthrough while applying water-flooding as enhanced oil recovery method, and need to design water injection well carefully (Fig. 9).

Fig. 7
figure 7

Air–brine capillary pressure of A and B sample from centrifuge

Full size image
Fig. 8
figure 8

Pressure drop and recovery analysis for imbibition oil–brine displacement experiment by RCP

Full size image
Fig. 9
figure 9

Oil-brine relative permeability curves of A and B sample from RCP program

Full size image

Summary and conclusions

  1. 1.

    An unsteady-state core-flooding system has been designed to determine dynamic relative permeability from measurements of pressure drop and production data. The system allows core sample to be held in reservoir condition, and records observations of pressure drop and production data automatically. Furthermore, the utilization of detector probe makes an improvement at breakthrough determination. And production data can be recorded accurately in cooperation with two-phase separator.

  2. 2.

    A numerical program combined capillary effect is constructed to analyze relative permeability through pressure drop and production data. This program has been validated via reference experiments and commercial reservoir simulation software. The program called RCP could be further applied to analyze the unsteady-state core-flooding experiment.

  3. 3.

    The RCP program can be adopted in the two-phase relative permeability curves computations for the unsteady-state data with high reliability. The parameter estimation approach overcomes significant limitations of the classic calculation procedure of the Johnson–Bossler–Naumann method and related methods. Furthermore, RCP is thought to give an occasion to calculate relative permeability curves for heterogeneous cores rather than the explicit methods, which applied for homogeneous cores only.

  4. 4.

    Two in situ core plug samples are used to investigate the oil–water relative permeability through designed system and RCP program. Both core-flooding system and RCP program show accurate results. Relative permeabilities of both Samples A and B show that water injection would cause oil flow to become tough, and make water breakthrough easy for water-flooding EOR method. It means that well position, spacing and pattern needed to be designed carefully.