Abstract
The relation between porosity and permeability parameters in carbonated rocks is complicated and indistinct. Flow units are defined with aim of better understanding reservoir unit flow behavior and relation between porosity and permeability. Flow units reflect a group of rocks with same geological and physical properties which affect fluid flow, but they do not necessarily coincide with boundary of facies. In each flow unit homogeneity of data is preserved and this homogeneity fades in the boundaries. Here, in this study, three methods are used for identification of flow units and estimation of average porosity and permeability in three wells of Tabnaak gas field located in south of Iran. These methods include Testerman statistical zonation, flow zone index (FZI), and cluster analysis. To identify these units, compilation of core porosity and permeability are used. After comparing results of flow units developed by these three methods, a good accordance in permeable zones was obtained for them, but for general evaluation of flow units in field scale, the methods of FZI and cluster analysis are more relevant than Testerman statistical zonation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Interpreting reservoir parameters are important and indispensable for development of oil and gas fields. Because of getting better perception about reserves and flow properties from hydrocarbon reservoirs and being a base for reservoir simulators, methods of interpreting reservoir parameters are valuable. Different methods result in description of hydrocarbon formation in different scales according to segregation ability, covering and number of measured parameters.
Many efforts had been taken to relate reservoir parameters and one of them is to relate porosity and permeability, so complexity of carbonated rock pore spaces always was very problematic.
Investigators tried to find a logical relation between these two vital parameters in hydrocarbon reservoirs. Assigning flow units is one of presented techniques that help to recognize permeable reservoir zones and relations of porosity and permeability.
Flow unit is a method for classification of rock types in pore scale according to flow properties based on geological parameters and physics of flow. These units are sections of the whole reservoir which have constant geological and petrophysical properties that affect fluid flow, and are different from other sections obviously (Abbaszadeh et al. 1996). Subsurface and surface studies had shown that fluid flow units are not always coincident with geological boundary. The concept of flow unit is a strong and peculiar tool for dividing reservoir into units which estimate inter-structure of reservoir in a compatible scale for reservoir simulation models (Abbaszadeh et al. 1996).
Permeability and porosity of reservoir rock are considered as the most important parameters for evaluation and estimation of reservoir (Shedid and Reyadh 2002). Besides, porosity vs. permeability diagrams have overmuch scattering and a weak correlation in heterogeneous carbonated reservoirs. Therefore, there is not any specific relation between these two.
Notwithstanding a close relation between porosity and permeability cannot be observed in a well, but with classifying and sorting data according to hydraulic flow units, a better zonation can be achieved. Considering the purpose, the selected scale, and available data, different ways exist for determination of flow units.
In this study, flow unit identification methods are used based on Testerman statistical zonation (Testerman 1962), flow zone index (FZI) (Amaefule et al. 1993), and cluster analysis (Holland 2006) and comparing these methods is done for three wells in Tabnak gas field.
Geology of studied location
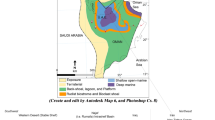
According to Oil and Gas Journal of National Iranian Oil Company (NIOC) (Insalaco et al. 2008), sweet gas field of Tabnaak was discovered in 2000. Tabnaak field is the largest onshore sweet gas field in Iran. This field is located in the south of Iran, in southwest of Lamerd, in east of Asalouyeh anticline. Hydrocarbon containing strata in this field are Dashtak, Kangaan, and upper Dalaan. Figure 1 shows position of Tabnaak gas field.
Tabnaak gas field position (Tiab and Donaldson 2004)
Data and methods
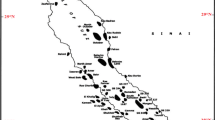
In this study, three methods are used for identification of flow units using core data from three drilled wells in subsurface strata of Tabnaak gas field. Position of these wells is indicated in Fig. 2. Here we studied the following methods.
Position of wells (Tiab and Donaldson 2004)
Introducing flow units using Testerman statistical zonation method
Statistical zonation came into attention after presenting the concept of flow unit. This method which was presented by Testerman, does not need any prejudgment about number of zones and also the number of zone boundaries are controlled automatically and by predefinition of an ending condition. In Testerman method zonation is done only using core permeability data. Testerman method is applied in two steps. These steps are:
-
(a)
Identification of flow units separately;
-
(b)
Assessing continuity of flow units in adjacent wells.
In the first step, each well was separately divided into zones or flow units. These zones are selected in a manner that the variance of quantities in each zone is minimum, and the variance between zones is maximum as possible. This method uses zonation coefficient “R” as a criterion for zonation. Equations (1), (2), and (3) were applied for zonation of each well:
where B is the variance between zones, L number of zones, W variance in each zone, m i number of permeability data in ith zone, j index for algebraically summation of data of each zone, i index for algebraically summation of zones, N number of total permeability data of reservoir, k ij permeability data of network (mD), R zonation coefficient, \(\overline{{k_{..} }}\) summation of average permeability data in well (mD), \(\overline{{k_{i.} }}\) average permeability data in ith zone (mD).
The coefficient “R” which is the best criterion for zone segregation has a value between zero and one; more its value close to one, the zones are more homogeneous. According to its definition, it cannot occupy a negative value and the negative values should be replaced by zero.
In separate zonation of each well, first of all permeability data in each depth should be identified. This process begins with first sample from highest depth and proceeds to lowest depth and then the zonation coefficient of each zone is calculated by Eqs. (1)–(3). Actually this coefficient indicates that how much homogeneously this zonation divides the zones. The more this coefficient close to one the more the zones are homogeneous. Therefore, the largest zonation coefficient obtains the most suitable zonation of well into two zones.
Then these steps repeat separately for each of two segregated zones. Division of zones proceeds until the yielding zonation coefficient in the next step becomes less than the previous.
After identification of flow units for each well the second part of calculations starts. This section interrelates the flow units in territory of reservoir from one well to another well for determination of flow units continuity. Calculations are done based on a statistical analysis comprising of difference between average data in adjacent well zones, and the difference which is expected from measurement of variance values in zones. Mathematical expression for this phrase is presented by Eq. (4):
where \(\overline{{k_{h.} }}\) is arithmetic average of permeability data for hth zone in a well, \(\overline{{k_{i.} }}\) arithmetic average of permeability data for ith zone in adjacent well, n i and n h are number of data for hth and ith zones, s standard deviation of total permeability data of reservoir, z tabulated constant as a function of data, number of zones and probability level, v, p used for identifying z as a function of probability level, “Z” values are presented in Harter (1960) table. If left side of equation is greater than the right side, according to statistics, zones differed from each other, and if the left side of equation is less than the right side, zones are related and continuous.
According to copious amounts of data and for attaining optimum zonation, hand calculation is not possible or at least faces numerous problems; therefore, for simplicity of operation and fast zonation, composing program code for calculations is inevitable. This code is composed in Matlab® software. Because of limitation in composing all the calculations, in this paper we choose to only mention outputs of well A as an instance. Table 1 shows permeability data and similar depths and Table 2 shows division of permeability data into three zones for well A. Equations (2)–(4) are used for calculation of variance between zones, variance in each zone, and zonation coefficient, respectively. “R” values in some points are negative which are substituted by zero for compatibility with its definition. As shown in Table 2, first step indicates zonation of well into two zones for which maximum value of R in boundary of zones is equal to 0.884265. In second step, data are divided into two groups and again using Eqs. (2)–(4) value of R for each group is calculated. Though maximum value of R for group 1 was 0.809522, this number is less than 0.884265, so the closing condition are executed and this group does not divide into other groups. But the maximum R for group two is 0.961796 which is more than 0.884265, so group two with coefficient of 0.961796 divides into another two zones. In third step, maximum R is less than 0.961796 so the closing condition executed and well A segregates into three zones. Tables 3, 4 and 5 show statistical indexes of core permeability data in three wells.
After all wells are zoned separately, assessment of continuity of wells is done using Eq. (5). This showed that the introduced zones in the interval of three studied wells are developed and continuous. Figure 3 shows cross section of three wells which indicates continuity of three adjacent wells with each other.
Flow zone index (FZI) method
Flow units (hydraulic) are identified based on FZI, in this method, which is product of dividing Reservoir quality index (RQI) by normalized porosity (φ z ) (Amaefule et al. 1993). Reservoir quality grows with produced number. RQI is an approximation of average hydraulic radius in reservoir rock and a key for hydraulic units and correlates between porosity, permeability and capillary pressure (Tiab and Donaldson 1996). FZI is also function of pore throat, tortuosity, and effective area based on texture properties, sedimentation model, pore geometry, and digenesis effects (Porras et al. 1999). Values of reservoir quality index, normalized porosity, and flow zone can be calculated by these equations.
Permeability (K) in above equations is in mD and φ e is a fraction. By taking logarithm of two sides of Eq. (7) we can write:
Equation (8) presents a straight line with slope of unity in RQI vs φ z diagram. Intersection of this straight line in φ z equals to one is the flow zone index. Samples which are on a straight line happen to have similar properties and so contribute to make a flow unit. Straight lines with slope of unity are firstly expected for non-shale-containing sandstone formation. Larger slopes identify shale formations. Rocks with detrital material have porous stratification, filling and fine grains generally; therefore, they indicate low amounts of FZI. In opposite, sands which have low amount of shale, large and sorted grains, low shape factor, and low tortuosity indicate large FZI. Different sedimentation environments, digenesis processes and reservoir geometry are controlling parameters for FZI (Tiab and Donaldson 2004).
There are different ways for zonation and identification of hydraulic flow units using flow zone index, including histogram analysis, probability diagram, and analytic classification algorithm. Graphical classification methods which include histogram analysis and probability diagram indicate FZI distribution visually, which makes it possible to define hydraulic flow units. Method which is used in this paper is “normal probability” (Soto and Garcia 1976). The number of break points or deviations in this diagram puts the number of hydraulic flow units in. Because of vast FZI changes logarithmic value is used. Figures 4, 5 and 6 show normal probability diagrams and hydraulic flow units for wells A, B, and C, respectively. These are plotted with Minitab® software.
Flow zone index does not necessarily depend on facies and different facies can be placed in one specific hydraulic flow unit.
According to the above three plots, it is obvious that each of the wells A, B and C is constituted of four, five, and seven hydraulic flow units, respectively. Logarithmic plot of RQI vs. φ z is linear with slop of 45°, in an ideal condition, and each line presents a hydraulic flow unit. The points which lines meet φ z = 1 are the average FZI for respective hydraulic units. Average FZI is useful for estimating permeability of the wells which have no cores. Relation between log RQI and φ z for each well is indicated in Fig. 7.
Tables 6, 7 and 8 show statistical permeability indexes of hydraulic flow units of wells A, B, and C, respectively.
Cluster analysis method
Cluster analysis method has been used for accurate segregation of data and identification of rock groups. The purpose of cluster analysis is to put a set of data in one group (known as clusters) in a manner that the data in one group have no severe differences and are homogeneous and inhomogeneous relative to other groups (Holland 2006). Cluster analysis puts the data in groups which are meaningful, beneficial, or both meaningful and beneficial (Loo et al. 2001). Maximum analogy (homogeneity) in a group and dissimilarity between groups implies optimum clustering (Loo et al. 2001). “Hierarchical clustering” is a method for contemporaneous grouping of data in different scales by clustered tree (dendriform). Output of this method is a graphical plot which is the so-called dendrogram or tree (dendriform), as it indicates structure of hierarchical clustering (Castillo et al. 1997). This tree is not a set of independent data; rather it is a multilevel classification in which the clusters in lower level rendered to upper levels (Holland 2006). This virtue allows us to choose which level or scale of clustering is more proper for the subject (Kadkhodaie-Ilkhchi and Amini 2009).
Hierarchical clustering analysis takes place in four steps which are: (a) calculating input vectors’ interspace; (b) establishment of parts related to interspacings; (c) creating cluster tree; (d) creating clusters.
-
(a)
Calculating input vectors’ interspace
Spacing between data variables is calculated in this step. For achieving this there are many functions available. One prevalent method used for input vector interspacing calculation or, as we can say interspace between every pair of data, is calculating Euclidean interspace between data which is defined as summation of difference between all data or variables. If we had two pairs of data (x 1, y 1) and (x 2, y 2) Euclidean interspace calculated by below formula:
Using Eq. (9) Euclidean interspace is calculated between all pairs of data.
-
(b)
Establishment of parts related to spacing’s
In this step it should be determined that which one of the created pairs of data should be placed in one cluster. Different methods exist for relating data and grouping them; here, the method of least squares between clusters (wards) is used.
-
(c)
Creating cluster tree
The cluster tree forms in this step using information yielded from degree of relation between data which places them in respected groups. Cluster tree is constituted by different sets of clusters, as each one of clusters is related to another cluster. In this kind of tree, horizontal axis includes number of data and vertical axis shows the amount with which different clusters associate with each other to form new clusters. There are different methods for creating cluster tree but in this study the method of “Agglomerative Hierarchical Clustering” is used. This method of clustering points out a series of clustering techniques with close relationship that each point is considered as a discrete cluster in them and repeatedly combines two clusters which are close to each other (according to interspacing); therefore, this method requires to define “proximity cluster” concept. Actually in cluster analysis calculation of proximity of two clusters is a key operation which is called proximity cluster. Amounts of minimum, maximum, and group average interspace are used for calculation of proximity cluster.
-
(d)
Creating clusters
After creating cluster tree by definition of a special level called “cutoff” we can introduce arbitrary large or small clusters. It is so important to select the foremost and proper number of plotted clusters; as the number of plotted clusters which entirely establish a cluster tree should reflect the most proper types of rock for carbonated rocks (Intera ECL Petroleum Technologies Ltd 1992).
Here in this study the cluster tree is plotted and number of clusters for each well was identified based on hydraulic flow units using Minitab ®. According to this, clusters of wells A, B and C are equal to (4), (5) and (7), respectively. Figures 8, 9 and 10 show dendrogram plot of three wells.
Tables 9, 10 and 11 show statistical permeability index of wells A, B, and C, respectively.
Results
Investigating relation between porosity and permeability in flow units
Though formations are generally interpreted as uniform and homogeneous, there is no specific relation between porosity and permeability. In the studied field, the sedimentary environment, geological parameters, and rock nature cause creation of geological complex and heterogeneous reservoirs. Then, as we can see in Fig. 11, there is no meaningful correlation between porosity and permeability in the studied well and a weak correlation coefficient (R 2) stands for these two parameters. In this section, we are attended to understand that if grouping permeability and porosity data could provide a specific relation for these two petrophysical parameters. Equipping a specific relation between porosity and permeability can be helpful for estimating permeability between wells.
Investigating relation of porosity and permeability in Testerman statistical zones
Since only permeability is used for zonation in Testerman statistical method and porosity is not considered for recognition of the flow units, it is not acceptable to expect a particular relation between porosity and permeability in each of the zones, see Fig. 12.
Investigating relation of porosity and permeability inflow zone index (FZI) method
Hydraulic flow unit is a pore scale method for classification of rock types relative to flow properties based on geological parameters and flow physics. Hence, relation between permeability and porosity in each hydraulic flow unit shows a powerful correlation between these parameters, see Fig. 13.
Investigating relation of porosity and permeability in cluster analysis method
Facies ordering, geological parameters and scale of pores are not considered in making clusters in grouping with cluster analysis method, albeit it is only statistical parameters and differences and similarities between permeability and porosity data which form the groups. So data with more statistical similarities are put into one group and there is no specific relation between porosity and permeability in each cluster, necessarily, see Fig. 14.
Transmissive hydraulic units (THU) and storage hydraulic units (SHU)
Identifying the units which have an important role in flow transmissivity and storage can be helpful in secondary recovery and more production of reservoir. According to acquired flow units from different methods, the question which types of data grouping are more precise in defining transmissive and storage hydraulic units are posed.
THU and SHU are defined using Lorenz plot for porosity and permeability data (Corbett et al. 2001). THU and SHU are identifiable in intersection of tangent and unit slope to Lorenz plot, if data of each flow unit be marked on Lorenz plot. Now we peruse THU and SHU in different flow units.
Identification of THU and SHU using Testerman method
Lorenz plot of three wells is shown in Fig. 15. Testerman statistical zones with different colors in diagram report that zones are scattered all over the diagram and none of them accurately specify THU and SHU. Therefore, Testerman method cannot be suitable for identification of transmissive and storage hydraulic units.
Identification of THU and SHU by FZI
Lorenz plot for three wells is shown in Fig. 16. Different colored hydraulic flow units on plot represent that unlike Testerman method, flow units are not scattered and brightly and accurately identify THU and SHU.
Figure 16 shows that hydraulic units of 1 and 2 in well A, 1 and 2 in well B, and 1 and 2 and 3 in well C have an substantial role on fluid transmissibility. In addition, hydraulic units of 3 and 4 in well A, 3 and 4 and 5 in well B, and 4 and 5 and 6 and 7 in well C have important role in fluid storage.
Identification of THU and SHU by cluster analyzing method
Lorenz plot for 3 wells in Fig. 17 shows that in cluster analysis, clusters almost have relative concentration and have a relative accuracy for identifying Transmissive and storage units. But accuracy in FZI method is much more than in cluster analysis.
Figure 17 shows that clusters 1 and 2 in well A, 1, 2 and 3 in well B, and 1, 2, 3 and 4 in well C have substantial effect on fluid transmissivity. In addition, clusters 3 and 4 for well A, clusters 5, 6 and 7 for well B, and clusters 5, 6 and 7 for well C have substantial effect on flow storage.
Compatibility of flow units
Because of difference between scales of flow units produced by different petrophysical data grouping methods, variations are obtained between them, but as Fig. 18 shows accordance with defined flow units based on FZI method and cluster analysis is higher than Testerman method. The reason for higher compatibility in FZI method and cluster analysis is using core porosity and permeability data in identification of flow units, but in Testerman method only permeability parameters are used for this identification.
Presented flow units with FZI and cluster analysis should be compatible in groups to be capable of reconciling between well interspaces, because detection of single flow unit in these methods is difficult and complicated. Therefore, for field scale qualifying of general situation and flow interval of reservoir, applying defined flow units based on Testerman is easier and faster.
In none of the above techniques, the type of facies is not significant and just potential reserve of the field is taken into consideration, because diagenesis processes had many effects on facies so that each facies can expose any porosity and permeability.
Conclusions
For identification of flow units in Tabnaak gas field different methods have been used in this study. Comprising them yielded following results.
-
1.
Using investigated methods it was understood that strong correlation between porosity and permeability was only found in flow units defined based on FZI method.
-
2.
FZI and cluster analysis are preponderant for identifying THU and SHU comparing to Testerman method, in this field.
-
3.
In this study it was understood that flow units identified by FZI and cluster analysis have a relative adequate compatibility.
-
4.
Compatibility and detecting a single flow unit based on FZI and cluster analysis in field scale are difficult if not impossible. Therefore, to characterize general situation and flow regime of reservoir in field scale, applying flow units identified by Testerman method is easier and faster.
-
5.
Only core permeability data are used in Testerman method; therefore, we face more limitations for recognizing zones with more separability potential, and also the number of yielded flow units is less than the two other methods.
References
Abbaszadeh M, Fujii H, Fujimoto F (1996) Permeability prediction by hydraulic flow units theory and applications, SPE Format. Evaluate 11:263–271
Amaefule JO, Altunbay M, Tiab D, Kersey DG, Kedan DK (1993) Enhanced reservoir description: Using core and log data to identify hydraulic (flow) units and predict permeability in uncored intervals/wells, SPE 26436. In: Presented at 68th Ann. Tech. Conf, and Exhibit. Houston, TX
Castillo E, Gutierrez JM, Hadi AS (1997) Sensitivity analysis in discrete Bayesian networks. IEEE Trans Syst Man Cybern 26:412–423
Corbett PWM, Ellabad Y, Mohammed K (2001) The Recognition, Modeling and Validation of Hydraulic Units in Reservoir Rock. In: 3rd Institute of Mathematics and its Applications Conference on Modelling Permeable Rocks, 27–29 March, Cambridge
Harter HL (1960) Critical values for Duncan’s new multiple range test. Biometrics 16:671
Holland MS (2006) CLUSTER ANALYSIS. Department of Geology, University of Georgia, Athens, GA 30602–2501 January
Intera ECL Petroleum Technologies Ltd (1992) Marun Field study, Phase 2, Reservoir characterization, Geophysics. Intera Petroleum Production Division, Calgary, Canada
Insalaco E, Virgone A, Courme B, Gaillot J, Kamali MR, Moallemi A, Lotfpour M, Monibi S (2008) Oil and Gas Journal The Iranian Oil Company (NIOC)
Kadkhodaie-Ilkhchi A, Amini A (2009) A Fuzzy logic approach To estimating hydraulic flow units from well log data: a case study from the Ahwaz oil field, South Iran. J Pet Geol 32:67–78
Loo BHA, Tan HTW, Kumar PP, Saw LG (2001) Intraspecific variation in Licuala glabra Griff. (Palmae) in Peninsular Malaysia a morphometric analysis. Biol J Linn Soc 72:115–128
Porras JC, Barbato R, Khazen L (1999) Reservoir flow units: a comparison between three different models in the santa Barbara and Pirital fields, North Monagas Area, Eastern Venezuela Basin. SPE 53671:1960
Shedid AS, Reyadh AA (2002) A new approach of reservoir description of carbonate reservoirs. SPE 74344:1–10
Soto R, Garcia JC (1976) Permeability prediction using hydraulic flow units and hybrid soft computing systems, 2001. In: SPE 71455. Stratigraphic Committee of Iran: Permo-Triassic rock stratigraphic nomenclature in South Iran (unpublished). NIOC, Tehran
Testerman JD (1962) A statistical reservoir-zonation technique. SPE J Pet Technol 14:889–893
Tiab D, Donaldson EC (1996) Petrophysics: theory and practice of measuring reservoir rock and fluid transport properties. Gulf Publishing, Houston, p 706
Tiab D, Donaldson EC (2004) Petrophysics: Theory and Practice of Measuring reservoir Rock and Fluid Transport Properties. s.l.: Gulf Professional Publishing
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mahjour, S.K., Al-Askari, M.K.G. & Masihi, M. Identification of flow units using methods of Testerman statistical zonation, flow zone index, and cluster analysis in Tabnaak gas field. J Petrol Explor Prod Technol 6, 577–592 (2016). https://doi.org/10.1007/s13202-015-0224-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13202-015-0224-4