Analysis of asphaltene deposition in Marrat oil well string: a new approach

Abstract

The amount of asphaltene is usually the minimum portion of crude constituents; however, due to its negative impact on the well performance and the overall efficiency of oil reservoir management, a large number of mostly academic studies are directed toward understanding the asphaltene behavior and mitigation of its deposition in flow processes from reservoir to process facilities. Typically, a small number of these are actual case studies. Among them is the asphaltene deposition in Marrat oil well string. In this particular case, significant amount of valuable field data were gathered for a long period of time under controlled conditions. By carefully reviewing the presented data in the original paper, we concluded that re-analysis of the field observation results, for improved understanding of the asphaltene deposition process, is necessary. By recalling the concept of liquid loading in the gas wells, the reduction of flowing well head pressure is interpreted due to the left asphaltene solid micelles in the well string. Also, we judge that the process of asphaltene deposition in the production tubing is a ‘seating and carving’ dynamic process, and at a critical thickness, the amount of asphaltene ‘cutting’ increases which is responsible for further pressure drop in the well tubing. By performing fundamentally simple calculations, the amount of asphaltene ‘left’ in tubing and the amount of asphaltene ‘cutting’ are computed. Also the minimum oil flow rate to handle and remove the asphaltene micelles is estimated in the Marrat case. Finally, we propose certain recommendations for future data gathering and optimum handling operation of asphaltene precipitation and deposition in well string.

Introduction

Asphaltene deposition in the pores of reservoir, in the flow string of wells, in the flow-line, and in the surface processing facilities is a recognized problem that affects the management of oil reservoirs. A broad range of efforts are made to resolve the issue; however, because of the varying nature of asphaltene, it becomes difficult to quantitatively characterize its structure and behavior, thus precluding a globally accepted solution. In each case (reservoir), to circumvent the problem, a unique method is presented. Even this unique method needs some form of adjustment or modification before applying it to a specific case.

A large number of researchers have worked on the issue. Their works can be categorized in two groups: those who investigate a theoretical model to justify the complicated behavior of asphaltene, and those who plan, set up, and perform a series of lab tests to formulate the asphaltene deposition. Of course, among them, there are researchers who attempt to utilize both approaches to demonstrate the robustness of their models. Unfortunately, few field data are available which are gathered under controlled conditions. In the mid 1960’s, Haskett and Tartera (1965) presented these types of data for Hassi Messaoud field in Algeria. In 2005, Alkafeef et al. (2005), in conjunction to propose a simplified method of predicting asphaltene deposition in tubing, published a set of gathered field data relevant to Marrat field of Kuwait.

There are other case studies for investigation of asphaltene problem in oil production from different reservoirs. Kharrat et al. (2012) worked on one of the Iranian light oil reservoirs. The reservoir and bubble point pressure were reported as 9200 and 4500 psi, respectively. After modeling the reservoir, they investigated the asphaltene behavior during production and suggested by controlling the well production rate at the optimum situation mitigate the asphaltene flocculation and deposition. Galoppini and Tambini (1994) studied the ultra-deep Villafortuna-Trecate (VF-TR) field. The density of oil was 40°API, and the GOR and bubble point pressure were reported as 618 scf/STB and 2578 psi, respectively. By measuring surface variables (pressure and rate), they calculated the equivalent productivity index (PI _eq). It was suggested that plotting the PI _eq versus cumulative oil volume has a linear trend. Thus, the change in the slope of this line would be an indication of asphaltene deposition in the vicinity of well bore. So, from history of wells, one can find the critical PI _eq at which the well should be stimulated for asphaltene removal. Sanada and Miyagawa (2006) reported the chemical treatment in one of Japanese oil reservoirs. They addressed the asphaltene deposition in the production separator and well tubing. The density of oil reservoir was around 38°API, and the formation comprised several sand bodies. After conducting a set of asphaltene dispersant tests (ADT), they used xylene plus a commercial asphaltene inhibitor for well stimulation treatment. They reported the treatment was successful.

The data gathered and published by Alkafeef et al. were obtained by a campaign of expensive activities carried out by different disciplines which are carefully supervised. In our opinion, the value of such field data is very high and thus we believe that it needs a careful review and analysis for better understanding of the phenomenon of asphaltene deposition in a well string. Additionally, in light of the recent lab work and theoretical efforts of better recognizing the phenomenon, one could approach the Marrat field asphaltene deposition problem in a clearer way. Based on this premise, we have made an attempt to provide a better interpretation and analysis of the Marrat field observation results to suggest a methodology for mitigating the effect of asphaltene deposition in other cases. Herein lies the purpose of this paper.

Statement of the problem

In conjunction with utilizing a well-monitoring technique in West Kuwait Marrat deep wells to monitor the well head flowing pressure, by using a caliper survey, the thickness of asphaltene deposition layer in well’s tubing is measured. All the following data and results are presented in the paper of Alkafeef et al.

• Asphaltene onset pressure (AOP) and bubble point pressure reported to be 3800 and 2400 psi, respectively (see Fig. 1 of Alkafeef et al.).

  Fig. 1

  

  Estimated Marrat well performance using PIPESIM

• It was observed that the average top of the obstructions was generally approximately 8000–9000 ft deep (see Fig. 2 of Alkafeef et al.).

  Fig. 2

  

  Estimated fluid flow gradient in Marrat well using PIPESIM

• A deposition thickness up to 0.35 in. was measured and attributed to asphaltene (see Fig. 3 of Alkafeef et al. for the asphaltene deposition thickness in the Marrat well determined by caliper log).

  Fig. 3

  

  Life history of a typical gas well

• During production, the well is adjusted to maintain flow rates to achieve an economic target. In Fig. 4 of their paper flowing well head pressure (FWHP), data versus time for Marrat well is presented. Alkafeef et al. recognized the following flow periods:

  • 1. Stabilization of FWHP at 1200 psig for about 1 month;

  • 2. Declination of the FWHP at a rate of −2 psig/day for a period of 130 days. They recognized that this drawdown is a characteristic of both the formation and reservoir fluid.

  • 3. Rapid declination of the FWHP at a rate of −7 psig/day for a period of 25 days. They referred to this period as the result of asphaltene deposition in tubing.

  • 4. Increase of the FWHP at a rate of +2 psig/day. This period is also attributed to the formation and reservoir fluid.

  Fig. 4

  

  Typical tubing performance curve

• By referring to data of their Fig. 4 and assuming the laminar flow condition in the well tubing and by employing Poiseuille’s equation $(Q \propto \frac{{\Delta Pr^{4} }}{\mu l})$, Alkafeef et al. concluded that the deposition thickness to radius of tubing ratio $(\gamma /r)$ can be calculated from the normal drawdown mechanism $(P/t)_{0}$ and the deposition mechanism $(P/t)_{1}$ slopes:

  $$ \frac{\gamma }{r} = 1 - \left[ {{\raise0.7ex\hbox{${\left( {\frac{P}{t}} \right)_{0} }$} \!\mathord{\left/ {\vphantom {{\left( {\frac{P}{t}} \right)_{0} } {\left( {\frac{P}{t}} \right)_{1} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {\frac{P}{t}} \right)_{1} }$}}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}} $$

  (1)

• They suggested that, as the well flowing pressure declines with time, both the onset of asphaltene flocculation point and bubble point pressures will simultaneously be shifted down along the tubing (see Fig. 5 of Alkafeef et al.).

  Fig. 5

  

  Schematic absolute roughness of pipe

Alkafeef et al. do not include the API, GOR, or B _o of the oil. There are also no data for the magnitude of maintained flow rate of well during the test. This information is essential to analyze the results of their field observations. To estimate them, the following methods are employed:

• From typical pressure profile of Marrat field, the fluid flow gradient is estimated to be in the range of 0.28–0.29 psi/ft. By considering that the flow rate was laminar, it can also be used as a good estimate of the static fluid gradient.

• With density of reservoir oil in the range of 40–42 lbm/ft³ and bubble point pressure of 2400 psi, it is expected that the GOR of the oil to be greater than 800 scf/STB. Also, this oil may have a viscosity less than 1 cP at the reservoir condition.

• Having the well string size and the FWHP (to be about 1250 psi) and by using PIPESIM, the well performance of a typical Marrat well during test can be estimated (see Fig. 1).

• As the FWHP is much less than bubble point pressure, it appears logical to encounter a reduction in flowing fluid gradient from the depth of bubble point pressure to well head pressure in the tubing (see Fig. 2).

By recalling the typical performance of gas wells or high GOR oil wells or oil wells with relatively high water cut and by referring to the first period of FWHP versus time, which demonstrates a stabilized FWHP for about 30 days, it seems that the interpretation of obtained results from Marrat well data gathering campaign needs to be revisited. Before applying this revision, we first review the theoretical basis of two phase flow performance in vertical conduits and also recall some concepts of asphaltene behavior.

Multiphase flow in vertical conduits

To calculate the hydraulic behavior of multiphase flow in pipes, different procedures are introduced which are based on identifying the flow regime in the pipe (Brill and Mukherjee 1999, Lyons 2010; Dale Beggs 1984; Szilas 1975). The important concept in this type of flow is ‘slip velocity.’ In multiphase flow, the individual phase velocities are quite different (Brill and Mukherjee 1999). Only for cases that are highly turbulent, dispersed-bubble-flow pattern and high velocity, annular-flow pattern, in which the fluids exist as homogeneous mixtures, are the phase velocities essentially equal. For all other cases, significant slippage can occur between lighter and heavier phases. Slippage will result in disproportionate amount of heavier phase being present at any given location in the well. This phenomenon is responsible for unsteady state in well string and also for loss of part of productivity of well both in gas and oil producers (Torre et al. 1987) which is known as casing heading and liquid loading in oil and gas wells, respectively. As it is more usual in gas wells, it is more studied in these types of wells under the category of ‘loading’ and ‘de-loading’ of liquid in gas wells.

Liquid loading in gas wells

By producing gas from gaseous region of hydrocarbon reservoirs, some liquids (in the form of condensed water or condensate) are generated in the transmission of gas from reservoir to surface facility systems. A part of these liquids produces in well string. In majority of gas reservoirs, the reservoir pressure is adequate to pump high quantities of gas, which means high velocity in well string. This high velocity can efficiently drain all generated liquid from well string. After decreasing the reservoir pressure below certain value, the production rate of wells falls below an amount that cannot handle the generated liquids in the tubing. The high slip velocity between gas and liquid phases causes some amount of liquid remaining in the well string and increases the static pressure gradient in the well string. By the time, the amount of liquid left behind gas in the well string increases and eventually ceases the flow (see Fig. 3 for a conceptual representation). The pressure drop in the tubing string basically consists of the hydrostatic pressure of the “loaded liquid” plus gas in the string and the frictional pressure loss due to flow. As it is shown in Fig. 4, by decreasing the well flow rate down to a specific rate, the pressure drop across the tubing decreases. After this point, by reducing the flow rate, the pressure drop increases. It is worth mentioning that Fig. 4 shows a typical tubing performance for Marrat well; however, it is primarily applicable for gas condensate wells and also for some oil wells.

In order to lift liquid in a gas well, it requires gas to provide sufficient energy to sustain all liquid droplets to travel upward or in suspension. To formulate the concept, the droplet is treated as a free falling particle with only two forces acting on it, which are drag force (F _D) in the flowing direction and gravitational force (F _G) in the opposite direction. The resulting equation is given below (Lea et al. 2008):

$$ V_{\text{T}} = \left[ {\frac{4g}{3}\frac{{d\left( {\rho_{\text{L}} - \rho_{\text{G}} } \right)}}{{C_{\text{D}} \rho_{\text{G}} }}} \right]^{0.5}, $$

(2)

where d is droplet diameter, C _D is drag coefficient equal to 0.44 for spherical objects, ρ _G and ρ _L and are gas and liquid densities, respectively.

Turner et al. (1969) by assuming the Weber number ($W_{\text{e}} = \frac{{\rho_{\text{G}} V_{\text{G}}^{ 2} d}}{\sigma }$) equal to 30 suggested the following equation:

$$ V_{\text{T}} = 1.92\left[ {\frac{{\sigma \left( {\rho_{\text{L}} - \rho_{\text{G}} } \right)}}{{\rho_{\text{G}}^{2} }}} \right]^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}}}, $$

(3)

where V _T is in ft/sec, σ is in dynes/cm and densities in lbm/ft³.

In the above formulation, Lea et al. (2008) considered surface tension of condensate as 20 dynes/cm and that of water as 60 dynes/cm.

Asphaltene characteristics

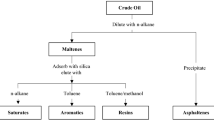
A crude oil at atmospheric pressure and ambient temperature has three main constituents: (i) saturates and aromatics, (ii) resins, and (iii) asphaltenes, Goual (2012). Asphaltenes are defined as the heaviest components of petroleum fluids that are insoluble in light n-alkanes such as n-pentane (nC₅) or n-heptane (nC₇) but soluble in aromatics such as toluene. The solubility class definition of asphaltenes generates a broad distribution of molecular structures. Asphaltenes and resins differ in color and texture. Asphaltenes are black, shiny, and friable solids, while resins are dark brown, shiny, and gummy.

Many factors affect the asphaltene deposition phenomena in the flow of petroleum reservoir fluids. Generally, in every flow regime (laminar or turbulent), it is always possible to find a narrow layer (the viscous or laminar sub-layer) of fluid near the wall. Within this layer, the dominating transport mechanism is molecular diffusion. In the center, on the other hand, the transport mechanism depends upon flow regime and the distribution form of momentum, heat, and mass species (Mirzayi et al. 2013). It is observed that the asphaltene deposition is a transient process. It is usually characterized by cycles of initial deposition followed by rapid incomplete erosion (Arsalan et al. 2014). In a dynamic deposition process in the well string, in addition to the effect of change in pressure, temperature, and composition, shear on the wall has a great impact on the asphaltene deposition.

The shear stress at the pipe wall is calculated as (Eskin et al. 2012)

$$ \tau_{\text{w}} = \frac{1}{8}\rho_{\text{f}} fV^{2}, $$

where f is the fanning friction factor that is a function of the pipe reynolds number and the wall surface roughness, V is the superficial flow velocity, and ρ _f is the fluid density.

There are limited data on the physical properties of asphaltenes. Asphaltenes are reported to have a density between 1.1 and 1.2 g/cm³ (Speight 2007), an atomic H/C ratio of 1.0–1.2, and a solubility parameter between 19 and 24 MPa at ambient conditions (Goual 2012). Asphaltene molecular weights are much more variable. However, results from advanced analytical techniques now agree that asphaltene molecular weight distributions are in the 400–1500 Dalton (Da) range, with a mean mass between 700 and 800 Da (Goual 2012). Surface tension between solid asphaltene and oil is not available in open literature.

The major factor that governs precipitation of heavy organic substances appears to be due to asphaltene flocculation, which is initiated due to variations in compositions of crude and injection (or blending) fluid, pressure, and temperature (Branco and Mansoori 2001). With alterations in these parameters, the asphaltene flocculation and, as a result, the nature of heavy organics which precipitate will vary. The concept that asphaltene molecules are present as a colloidal system is credited to Nellensteyn (1924). He proposed that asphaltic compounds are made of flocs or aggregates of asphaltene protected by adsorbed resin and hydrocarbon materials, all dispersed in a hydrocarbon medium. Leontaritis and Mansoori (1987) proposed a thermodynamic colloidal model which is capable of predicting the onset of asphaltene flocculation. According to this model, asphaltenes exist in the oil as solid particles in colloidal suspension, stabilized by resins adsorbed on their surface.

After flocculation (precipitation) of asphaltene particles and forming of micelles, we believe that absolute roughness (ε) of surface pipes will help the deposition (see Fig. 5 for a conceptual representation). Let us consider the forces that act on an asphaltene particle attached to the wall as considered in Fig. 1 of Eskin et al. (2011). This particle is under the action of several forces. The van der Waals attraction force F _A is the only force keeping particles at the wall. The shear-induced lift force F _L is oriented in the opposite direction to the van der Waals force. The drag force F _D that is significantly larger than the lift force (Sweeney and Finlay 2007) is directed along the wall. It is clear that the particle located on the rough wall is also under the action of a torque caused by the drag force. The friction force F _fr is considered to be composed of both the surface friction and the rolling friction components. The ‘a’ and ‘b’ are levers which are assumed to be equal. δ _L is thickness of laminar sub-layer.

Re-interpretation of the Marrat results

Before re-interpreting the results of Marrat well data gathering campaign, let us consider a few points which should be kept in noted during the review of the asphaltene precipitation process in Marrat well.

• The provided data are not sufficient for full and standalone understanding of the situation and interpretation of the problem. The well data including PVT, well test, PLT, GOR, and oil production rate were available but are not provided in the paper.

• The well head pressure is not a perfect variable for prediction and interpretation of the fluid behavior in the well string, especially in high GOR wells. The major pressure drop in the well string, especially as oil produces, is gravity (static head) of fluid. By displacing the depth of bubble point pressure in the well string, the amount of separated gas in the well string will change and consequently the length of tubing having lighter fluid will change and it will affect the FWHP. As seen in Fig. 1, above the depth of 5000 ft, the fluid gradient smoothly and monotonically decreases due to reaching the bubble point pressure and start of release of the associated gas. By changing the conditions, the length of tubing having the free gas will change and will consequently impact the FWHP. By shifting the bubble point pressure downward in the well string, more length of tubing will have free gas. This means that the change in FWHP could not just be attributed to asphaltene flocculation/deposition in the well string; however, for sake of simplicity, we ignore this effect and assume that all FWHP changes were due to the precipitation/deposition of asphaltene in the well string.

• Based on the data provided, we assume that during the data gathering, the change in flowing bottom hole pressure (FBHP) is negligible. This assumption is based on the stabilized flowing pressure for 30 days (see Fig. 4 of Alkafeef et al.).

It is generally accepted that the process of asphaltene deposition takes place in two steps: precipitation (flocculation) and deposition (aggregation). The path between these two steps is not fully understood; however, variables such as pressure, temperature, composition, and the velocity generally influence this process. As it is mentioned, asphaltene particles (micelles) are solids. In the reservoir and under the static conditions, the resins adhere to these micelles and retain them in bulk of fluid as a suspended particle. The resins also prevent adherence of the micelles to each other. The role of resins with the presence of asphaltene in the oil is the same as that of dual-acting agents in an emulsion of water in oil. Water is not normally soluble in oil but the dual-acting agents help them to be suspended in the oil. Suspension of two immiscible liquids is called emulsion, and suspension of solids in liquids is named colloid. It seems that tendency of resins having connected to normal alkane is higher than affinity to asphaltene. At high pressure, the molar volume of normal alkane is very low; consequently, their activity is low. By decreasing the system pressure, the molar volume of normal alkanes increases and starts to have more connection to resins and this causes to reduce the amount of resins available for retaining the solid asphaltene particles in the solution. Below bubble point, by releasing the low molecular weight alkanes from oil, again the availability of resins to help the asphaltene micelles to be a part of solution increases.

After asphaltene precipitation, if it is not removed from the system, it will eventually deposit on the available surfaces. In flowing oil wells, after flocculation of asphaltene, three events will simultaneously happen in wells string:

• (a) Part of it (flocculated asphaltene) is removed by flowing fluid,

• (b) Part of it is deposited on the tubing/casing surface,

• (c) And part of it is left suspended in the well string.

The proportion of each of these parts to total precipitated asphaltene depends on several factors such as pressure, temperature, physicochemical structure of flocculated asphaltene, the physicochemical structure of the surface of the pipe, and more importantly the in situ velocity of the fluid.

The ‘left’ part of precipitated asphaltene in well string is responsible for the increase in the density of flowing fluid which will consequently increase the static pressure drop along the tubing and decrease in FWHP. Based on the experience from multiphase flow in gas wells or high water cut oil wells, the left asphaltene micelles do not remain suspended at the same depth which comes out of solution but drops to the bottom of the well string even below the AOP depth. If all variables are retained under control and are dynamically kept constant, the amount of ‘left’ asphaltene per unit time will remain constant. So, the increase in total static pressure drop across the well string per unit time and the ‘reduction’ per unit time in FWHP will also remain constant. This is what happened in the second region of Marrat well dynamic data gathering (see Fig. 4 of Alkafeef et al.), which caused more or less a constant pressure drop (2 psig per day) on the FWHP for about 130 days.

It is believed that as early as asphaltene precipitated in the tubing, part of it is deposited on the wall of tubing. It seems that deposit layer profile in the tubing follows a triangular shape. The same phenomena can be seen in nature. There are three modes of sediment transport by wind (and in this case by flow of oil): creep or reptation; saltation, and suspension (Lancaster 2009). The process of asphaltene deposition can be assumed to be more or less the same as those processes which happen in nature for generating the sand dunes by wind. This means that the deposition process is a dynamic one and is not a static development. By ‘dynamic,’ we mean that the deposition and asphaltene returning back to flow stream are in a dynamic equilibrium. Also, we believe that the ‘deposited asphaltene profile’ in tubing has a repeated form but with different thickness along the tubing length (see Fig. 6). By the time, the thickness of ‘deposited’ asphaltene on the tubing surfaces increases; this will cause increases in velocity of fluid in that portion of tubing. After the thickness of deposit reaches a critical value, the shear on the wall will start to play its main role carving the deposited asphaltene from the wall surfaces. These ‘cuttings’ cannot again deposit on the wall and will be carried by main flow stream. These ‘cuttings’ also impose further pressure loss on the energy of system which will cause additional decrease in FWHP. This is what happened in the third region of Marrat well dynamic data gathering (see Fig. 4 of Alkafeef et al.), which caused more or less a constant pressure drop (7 psig per day) on the FWHP for about 25 days. Part of this pressure drop is attributed to previous process.

Fig. 6

Conceptual representation of deposited asphaltene in tubing

By the time the column of well string that contains ‘left’ asphaltene micelles increases and eventually it reaches the well head, it starts to exit the well string. At the steady-state conditions, from this time onward, no change in the FWHP would be expected; however, by increasing the thickness of the deposited asphaltene and due to reduction in flow path, the velocity of fluid in that interval of tubing will increase. This increase in fluid velocity means an increase in ability of the energy of system to handle more solid asphaltene particles and consequently more draining of asphaltene micelles. The process of draining more asphaltene causes to lighten the column of fluid in the well string. This, in turn, results in increase in FWHP. This is what happened in the fourth region of Marrat well dynamic data gathering (see Fig. 4 of Alkafeef et al.), which caused more or less a constant pressure increase (2 psig per day) on the FWHP for about 50 days.

Finally, based on the foregoing analysis, there are four successive flow periods that we identify: (1) normal flow; (2) asphaltene loading and deposition; (3) asphaltene carving; and (4) asphaltene de-loading.

Supporting calculations

Based on the discussion and interpretation made previously for the Marrat field results, we now present various relevant calculations in the following sections.

Amount of “left” asphaltene in the well string

The ‘left’ asphaltene causes the fluid in the tubing to become heavier. This in turn will result in higher pressure drop. This pressure drop results in a reduction in FWHP. From basic fluid mechanics, one can write

$$ \Delta P = \rho gh\;{\text{or}},\;\Delta P = G_{\text{f}} h, $$

(5)

where $\Delta P$ is static pressure drop in psi, $G_{\text{f}}$ is fluid gradient, $\rho g/144$ in psi/ft, and h is vertical length of tubing in ft.

Thus, the change in static pressure drop can be computed as follows:

$$ \Delta (\Delta P) = (\Delta G_{\text{f}} )h $$

(6)

$$ \Delta G_{\text{f}} = \{ G_{\text{f}} \left[ {1 - \left( {wt} \right)_{\text{A}} } \right] + G_{\text{A}} \left( {wt} \right)_{\text{A}} \} - G_{\text{f}}, $$

(7)

where G _f and G _A are oil and asphaltene gradient, respectively and $\left( {wt} \right)_{\text{A}}$ is asphaltene weight fraction of ‘left’ asphaltene in the tubing.

$$ \Delta G_{f} = [G_{A} - G_{f} ]\left( {wt} \right)_{A} $$

(8)

By combining Eqs. (6) and (8):

$$ \left( {wt} \right)_{\text{A}} = \frac{{\left( {\Delta (\Delta P)} \right)}}{{[G_{\text{A}} - G_{\text{f}} ]h}} $$

(9)

Let us use Eq. (9) to estimate the weight percent of ‘left’ asphaltene in the Marrat well string. The asphaltene specific gravity is considered to be 1.2 (water = 1.0).

$\left( {\Delta (\Delta P)} \right) = 2\left( {{\raise0.7ex\hbox{${\text{psi}}$} \!\mathord{\left/ {\vphantom {{\text{psi}} {\text{day}}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\text{day}}$}}} \right) \times 155\left( {\text{day}} \right) = 310 {\text{psi}}$; h = 15,000 ft, G _f = 0.28 psi/ft and G _A = 1.2 × 0.433 = 0.52

Therefore, $\left( {wt} \right)_{\text{A}} = \frac{{\left( {\Delta (\Delta P)} \right)}}{{[G_{\text{A}} - G_{\text{f}} ]h}} = \frac{310}{(0.52 - 0.28) \times 15000} = 0.0861 \,{\text{or}}\, 8.61\;\% .$

Note that this is the amount of asphaltene which is just left in the well string in flocculated form in the ‘effected interval’; and it is not the total asphaltene of crude nor the total separated asphaltene in the well string. The average daily ‘effected interval’ (daily increase in well string length that contain the ‘left asphaltene’) is about 97 ft (15,000 ft/155 day).

Let us now compute the mass of ‘left’ asphaltene in tubing and the mass of asphaltene content of typical crude.

$$ V_{\text{t}} = \, V_{\text{f}} + \, V_{\text{A}} $$

(10)

$$ hS = \frac{{m_{\text{f}} }}{{\rho_{\text{f}} }} + \frac{{m_{\text{fA}} }}{{\rho_{\text{A}} }} $$

(11)

$$ m_{\text{f}} = \left( {\frac{{1 - \left( {wt} \right)_{\text{A}} }}{{\left( {wt} \right)_{\text{A}} }}} \right)m_{\text{A}} $$

(12)

Combining Eqs. (11) and (12):

$$ m_{\text{A}} = \frac{hS}{{\left\{ {\left( {\frac{{\left( {\frac{{1 - \left( {wt} \right)_{\text{A}} }}{{\left( {wt} \right)_{\text{A}} }}} \right)}}{{\rho_{\text{f}} }}} \right) + \frac{1}{{\rho_{\text{A}} }}} \right\}}} $$

(13)

In this case, h = 97 ft, S = tubing cross section area = 0.03376 ft², $\left( {wt} \right)_{\text{A}} = 0.0861$, $\rho_{\text{f}} = 42 {\text{lbm}}/{\text{ft}}^{3}$, $\rho_{\text{A}} = 1.2 \times 62.4 = 74.9\;{\text{lbm}}/{\text{ft}}^{3} .$

By using Eq. (13), the mass of asphaltene ‘left’ is estimated to be about 12.3 lbm/day.

Amount of asphaltene content in well stream

To estimate the possible amount of asphaltene in well stream, we consider the following assumptions and calculations. Another form of Eq. (12) is

$$ m_{\text{A}} = \left( {\frac{{1 - \left( {wt} \right)_{\text{A}} }}{{\left( {wt} \right)_{\text{A}} }}} \right)m_{\text{o}} $$

(14)

$$ m_{\text{A}} = \left( {\frac{{1 - \left( {wt} \right)_{\text{A}} }}{{\left( {wt} \right)_{\text{A}} }}} \right)(5.615\;q_{\text{o}} B_{\text{o}} \rho_{\text{o}} ), $$

(15)

where $q_{\text{o}}$, $B_{\text{o}}$, and $\rho_{\text{o}}$ are oil rate (STB/day), oil formation volume factor (rbbl/STB), and in situ oil density (lbm/ft³), respectively. From the data provided, the in situ oil density is about 41 lbm/ft³, and B _o is assumed to be 1.35 rbbl/STB. The amount of asphaltene content of a well stream at a rate of 100 STB/day and just 1 wt% of asphaltene would be about 314 lbm/day. It means that even with oil rate of as low as 100 STB/day (in Marrat case) and the asphaltene content as low as 1 %, expected asphaltene precipitation is much higher than that ‘left’ in the well string.

Amount of ‘carved’ asphaltene

As mentioned previously, from the initial time of precipitation of asphaltene, its deposition on the surface of tubing walls begins; however, this process takes place under the situation of a dynamic equilibrium (deposition and return to the main well stream, at same time but the rate of deposition is higher than coming back). By increasing the thickness of deposited asphaltene, the effect of shear stress becomes more important, and at a critical asphaltene thickness, some of the deposited asphaltene is cut by flow and is suspended in the well stream. This carved asphaltene is responsible for extra pressure drop as seen in the third region of Fig. 4 of Alkafeef et al. We supposed that part of the pressure drop in this region is due to the flocculation of left asphaltene. So, it is assumed that the pressure drop of 5 psig/day is due to the ‘carved’ asphaltene. By using Eqs. (9) and (13), the wt% of ‘carved’ asphaltene (in well stream) and its weight are estimated to be 3.47 % and 30.0 lbm/day, respectively. Note that it is assumed that the flocculation of ‘carved’ asphaltene affects the entire length of the well string, i.e., 15,000 ft.

Tubing length of deposited asphaltene

In the fourth region of Fig. 4 of Alkafeef et al., by increasing the fluid velocity in the asphaltene deposited tubing section, the ability of flow to carry out the asphaltene micelles increases as it can remove some of the flocculated asphaltene out of the tubing. For this reason, the FWHP is increased. As the pressure gain on well head pressure is about 2 psig/day, it is assumed that the same calculation which is carried out for region 2 is also applicable here. As the length of ‘effected interval’ in region 2 is about 97 ft/day, we assumed that in region 4, the same length of ‘effected interval’ is drained. So, the effective length of deposited asphaltene in the tubing is estimated to be about 4850 ft (97 × 50).

Maximum amount of deposited asphaltene

As it is mentioned, it is believed that the form of asphaltene deposition in the tubing is not cylindrical; however, for sake of simplicity, we assume that deposited asphaltene has this geometry. So, by recalling the annulus length of this precipitated asphaltene from previous Sect. (4850 ft), the maximum amount of asphaltene can be estimated to be around 5556 lbm or a rate of deposition of 37 lbm/day.

Minimum flow rate calculation

To calculate the minimum flow for handling the asphaltene micelles, it is assumed that Turner’s equation is applicable (Eq. 3). We did not find any sources for surface tension of asphaltene-oil; however, based on some of the reported solid–liquid interfacial tensions by Bahramian and Danesh 2004, we considered a value of 0.5 dynes/cm to be representative. Also, we assume the density of oil and asphaltene to be 42 and 74.9 lbm/ft³, respectively. Therefore the ‘terminal velocity’ is estimated to be about 0.6 ft/sec. This velocity is equivalent to 231 and 126 STB/day for tubing diameter of 2.488 in. and 1.84 in, respectively.

Discussion

Asphaltene deposition in Marrat well is one of the exceptional cases in which a lot of actual field data were gathered under controlled conditions for a long period of time (about 235 days). Therefore, we believe valuable lessons can be learned for managing asphaltene issues in other cases, and for this reason, we have included further discussion in this section.

The asphaltene precipitation and deposition is very complicated phenomenon even under static conditions. By the addition of shear stress on the other impacting parameters, it becomes even more complex. To understand and formulate this process, not only is it necessary to carry out an extensive pre-planned set of lab activities, but also having a large amount of field data which are gathered under controlled conditions is essential. After flocculation of asphaltene, a large amount of precipitated asphaltene is drained from well string by flow stream and just a small amount of it remains in the well string which exerts an extra pressure drop across the well string. Also, even though the deposited amount of asphaltene is not significant; however, by the time it accumulates, it becomes problematic.

In this discussion, we also include the following three key points pertaining to the Marrat field observations:

• The deposition of asphaltene is a dynamic-reciprocating process.

• The deposition would continue up to a point that eventually ceases the flow. In the Marrat case, it is believed that after the asphaltene de-loading process, a new condition is established which causes repetition of the previous ‘flocculation-deposition’ cycle and increases the thickness of deposited asphaltene. These cycles repeat with shorter successive periods until plugging of the flow path.

• Precipitation takes place in the window of dynamic asphaltene onset pressure (DAOP) and bubble point pressure in tubing; however, due to the gravity effect, the flocculated asphaltene micelles occupy from bottom of well string up to well head. It means, sooner or later, these solid micelles would precipitate in the porous media in the vicinity of well bore especially after shut in of the well.

Finally, as part of the discussion, we present the following equations that allow the determination of time to fill-up the well string with asphaltene flocs.

For a constant rate or at least one choke size, record the decrease in FWHP per day for a period of time (ΔPw). From the following equations, estimate the time necessary to fill up the well string from TD (total depth) to surface:

Another version of Eq. (9):

$$ \left( {wt} \right)_{\text{A}} = \frac{{ \Delta P_{\text{w}} }}{{[G_{\text{A}} - G_{\text{f}} ]h}}, $$

(16)

where $\left( {wt} \right)_{\text{A}}$ is wt% of asphaltene left in the well string, $\Delta P_{\text{w}}$ is the flowing well head pressure drop in psi/day, and h is the tubing length which is filled up by asphaltene floc in ft/day.

By assuming constant FWHP drop, the time (in day) to fill up whole well string would be

$$ t_{\text{fill up}} = \frac{TD}{h} $$

(17)

Combining Eqs. (17) and (18):

$$ t_{\text{fill up}} = \frac{TD}{{\Delta P_{\text{w}} }}\left( {wt} \right)_{\text{A}} [G_{\text{A}} - G_{\text{f}} ] $$

(18)

In Eq. (18), all parameters on the right-hand side are known except $\left( {wt} \right)_{\text{A}}$ which should be obtained from lab tests.

Recommendations

Based on the foregoing analysis and discussion of the Marrat field observation results, we offer the following recommendations as suggestions for future field test and certain lab design parameters. We believe that these recommendations will be helpful in better management of asphaltene issues in other cases.

• 1. Perform all pre-test activities including cleaning the well, start the flow from stabilized well pressure, flow the well under constant, controlled rate, use the well head pressure recorder system.

• 2. Measure the amount of asphaltene in the reservoir oil.

• 3. Employ two parallel mesh strainer type design before choke or any other flow controller device (see Fig. 7).

  Fig. 7

  

  Schematic of proposed parallel strainers

• 4. By using these two strainers, the amount of asphaltene, leaving in the flocculated form, in the well string can be estimated. Based on the amount of asphaltene content of original oil, the amount of asphaltene ‘left’ or ‘deposited’ can be computed.

• 5. By using Eq. (16) and the procedure outlined in “minimum flow rate calculation,” design and employ an appropriate tubing size for removal of the asphaltene flocculates.

• 6. Measure the surface tension between asphaltene solid and oil.

• 7. For asphaltene deposition inhibition, formulate a chemical which by sticking to solid asphaltene flocs will help lower their effective density and help their carry over.

• 8. From the operational standpoint, changing the production rate (above the minimum required rate) can delay the asphaltene plugging of the tubing.

• 9. After normal shut in of the well, asphaltene deposition in the porous media near the well bore is possible. Before re-opening the well, flush the rock near the well bore by appropriate solvent, to clean the formation.