Well test, rate transient analysis and reservoir simulation for characterizing multi-fractured unconventional oil and gas reservoirs

Abstract

Unconventional reservoirs such as shale gas and shale oil have become an increasingly important source of energy in the USA with potential reservoirs identified worldwide. Due to the insufficient permeability of the shale reservoirs, they require efficient stimulation using multi-stage hydraulic fractures to produce gas in commercial quantities. A critical challenge in the reservoirs is performance evaluation of the fracturing and characterization of the stimulated reservoir volume (SRV) for permeability and hydraulic fracture size. Conventional well test analysis in multi-stage fractured shale reservoirs may not provide reliable results due to the extensive wellbore storage effect, fracture complexities, and heterogeneity of the low-permeability reservoir. To overcome such issues, advanced well test analysis techniques integrated with rate transient analysis can be used to reduce uncertainties associated with estimation of the reservoir and hydraulic fractures’ dynamic parameters. This paper proposes a practical methodology and workflow for characterizing the SRV parameters in multi-fractured wells in unconventional oil and gas reservoirs using well test and rate transient data analysis based on diffusivity equation solution for linear and elliptical flow regimes integrated with numerical reservoir simulation. A reservoir simulation model is built and run for a typical fractured shale reservoir to verify the reliability of the proposed simplified approach. Furthermore, multi-fractured unconventional reservoir field examples of well test analysis, reservoir simulation and history matching are presented to show how the stimulated reservoir volume can be characterized to perform a more reliable production forecast in shale oil and shale gas reservoirs.

Introduction

Unconventional reservoirs such as shale gas and shale oil have become an increasingly important source of energy worldwide. Due to the insufficient permeability of the shale reservoirs, they require efficient stimulation using hydraulic fractures to produce hydrocarbon in commercial quantities (Bagherian et al. 2010).

The propagation and direction of hydraulic fractures are influenced by many factors but are primarily controlled by in situ stresses. Where there is high contrast between minimum and maximum horizontal stresses, the stimulation creates a narrow or linear fracture fairway, and where the stress contrast is low, wide or complex fracture geometry is created during the treatment as shown in Fig. 1 (Fan et al. 2010). Considering a horizontal well in a normal faulting stress regime, if the horizontal well is drilled in the direction of maximum horizontal stress, the longitudinal hydraulic fractures are likely to be initiated along or parallel to the wellbore, and if the horizontal well is drilled in the direction of minimum horizontal stress, then the transverse hydraulic fractures are initiated perpendicular to the wellbore axis as shown in Fig. 2 (Hossain and Rahman 2008).

Fig. 1

Effect of stress anisotropy on propagation of hydraulic fractures (Fan et al. 2010)

Fig. 2

Effect of wellbore direction on hydraulic fractures propagation

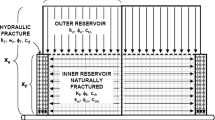
In term of characteristics, shale reservoirs’ properties may change in different zones in areal and vertical directions, and along a horizontal wellbore, the well may intersect a consecutive series of some zones with higher porosity, lower water saturation and higher total organic content (productive shale intervals), and some zones with high water saturation, low effective porosity and low total organic content (non-productive shale intervals). Also at the well location, although the well may penetrate a productive shale, but in the same interval, away from the well location there might be non-productive shale sections. In other words, in unconventional shale reservoirs, productive shale zones and non-productive shale sections have randomly been distributed as illustrated in Fig. 3. Therefore, a common practice in unconventional reservoirs is to drill a horizontal well, complete the well with series of perforated intervals with an specific spacing and length to control where the fracturing stages to be regardless of where the productive shale zones are at wellbore location, and then hydraulically fracture the whole formation along the wellbore in multi-stages to create a stimulated reservoir volume (SRV) with an enhanced effective permeability around each hydraulic fracture that has gone through productive and non-productive shale sections.

Fig. 3

Basic concepts related to multi-fractured wells (dual-porosity dual-permeability SRV)

In the case of a hydraulic fracture network around the wellbore where fracturing creates a stimulated reservoir volume as shown in Fig. 3 (the typical scenario in shale reservoirs), the main SRV parameters are the reservoir thickness (h), SRV permeability (K _SRV), fracture half-length size (X _f), fracture spacing (2 × Y _e ), drainage area (A), and cross-section area (A _c). In the simplified analytical methods used in studying shale gas and shale oil reservoirs, it is assumed that the whole SRV is homogeneous productive shale. For the SRV shown in Fig. 3, the drainage area (A) and the cross-section area perpendicular to the flow (A _c) can be defined as follows, considering ‘n’ stages of hydraulic fractures (Arevalo et al. 2002):

$$A_{\text{c}} = n \times 2 \times \left( {2X_{\text{f}} \times h} \right)$$

(1)

$$A = n \times 2X_{\text{f}} \times 2Y_{e}$$

(2)

The SRV is a network of hydraulic fractures and untreated matrix which are randomly distributed in the dual-porosity and dual-permeability system. The main SRV parameters are SRV permeability, hydraulic fracture spacing (shale matrix block size) and SRV porosity (volume of the open fractures inside the stimulated reservoir volume). Characterizing the SRV parameters is a critical challenge as it indicates the effectiveness of the stimulation of the low-permeability shale, the efficiency of the drained volume due to well spacing, and the well future production performance.

One of the common methods for characterizing the dynamic reservoir parameters is well testing, in which the pressure transient data are recorded and analyzed using the plot of transient pressure and its derivative versus time on Log–Log scale. The test data are normally analyzed using a diagnostic plot to identify the radial flow regime and calculate the average permeability of the reservoir accordingly. In a conventional reservoir, wellbore storage effect may last few hours, and then in few days the reservoir will exhibit its average properties upon reaching infinite acting radial flow regime. However, for multi-fractured unconventional reservoirs, things are radically different because of the large drop in mobility, fracture complexities, and heterogeneity of the low-permeability formation that cause an extensive wellbore storage effect and slow propagating pressure pulse into the formation. As a result, we may have to wait months or years to detect the complicated flow regimes in the drainage area around the wellbore and fractures, and maybe centuries to eventually detect the equivalent infinite acting radial flow regime (KAPPA Engineering 2015). Therefore, using the conventional well test analysis to characterize the SRV parameters in multi-fractured shale reservoirs may fail to provide reliable results, and advanced techniques may be required.

Reservoir flow regimes in hydraulically fractured wells

A pressure transient test breaks into several flow regimes, each seeing deeper in the reservoir than the last. Depending on the well completion type and the reservoir geological and geometric attributes, different flow regime might be revealed on pressure transient diagnostic plots. In conventional well test analysis, diagnosis of the radial flow regime is critical in quantitative well test interpretation, since a reliable value for reservoir permeability can be estimated when the late-time radial flow regime is established in the reservoir (Badazhkov 2008; Bourdarot 1998).

In the case of a multi-fractured well as illustrated in “Appendix A” and shown in Fig. 4, the main reservoir flow regimes after wellbore storage effect, are the early-time linear flow regime towards the hydraulic fracture wings in SRV in the vicinity of the fractures, the early-time elliptical flow regime in the SRV towards the drainage area of linear flow perpendicular to each hydraulic fracture, and the early-time boundary-dominated flow when stimulated reservoir volume, SRV, around each hydraulic fracture is depleted. After the SRV depletion, hydrocarbon flow is provided from untreated shale around SRV (the untreated reservoir rock surrounding the stimulated reservoir volume acts as boundary).

Fig. 4

Simplified reservoir flow regimes (linear, elliptical and pseudo radial) in multi-fractured shale reservoirs

After the reservoir flow regimes in the SRV, the SRV boundary-dominated flow effect is then followed by linear flow regime inside the untreated reservoir zone towards the drainage area of the multi-stage fractured well (Fig. 4c), then elliptical flow regime, and finally at late time when pressure disturbance propagates deep enough into the reservoir, a pseudo radial flow regime is established (Fig. 4d), with slope of zero on pressure derivative. On the pressure derivative curve based on solution of radial flow diffusivity equation, the slope of +1 shows wellbore storage effect, the slopes of −0.5, +0.5, +0.25 and +0.36 indicate spherical, linear, bi-linear and elliptical flow regimes, respectively, and the slope of zero indicates radial flow regime. In typical testing time duration in multi-fractured shale reservoirs, only the early-time flow regimes might be the ones that can be detected on the diagnostic plots, but not the late-time flow regimes.

In multi-fractured shale reservoirs, field observations indicate that the early-time linear flow regime and the early-time elliptical flow regime are established in the SRV, but radial flow regime cannot be established in the SRV. The reservoir flow regimes in SRV are followed by the SRV boundary-dominated effect. Well test analysis methods such as rate transient analysis (RTA) and pressure buildup analysis (PBA) in the multi-fractured wells require analyzing the reservoir flow regimes that are detected on well test analysis diagnostic plots, to characterize the SRV dynamic parameters.

Rate transient analysis (RTA) for multi-fractured shale reservoirs

In rate transient analysis for oil wells, the pressure data are normalized using the rate data, and then the RTA plots are made to characterize SRV parameters. For gas wells, bottom-hole pressure, P, should be converted to pseudo pressure, m(p), and then the pseudo pressure data are normalized using gas production rate. The normalized pressure data are used to make the following RTA plots for SRV characterization (Malallah et al. 2007):

• A plot of the normalized pressure (d[P _wf]/d[Q]) versus time (d[t]) on the Log–Log scales as shown in Fig. 5a can identify the data points related the linear flow regime based on the line slope of ½ on the diagnostic plot. When the slope increases from ½ to higher values, this indicates the time at which the boundary-dominated flow effect starts (t _BDF). For gas wells, normalized pseudo pressure should be plotted versus time as shown in Fig. 5c.

  Fig. 5

  

  Oil and gas wells RTA

• A plot of the normalized pressure (d[P _wf]/d[Q]) versus (d[t ^½]) as shown in Fig. 5b can provide slope of the linear flow regime straight line (m _LF). For gas wells, normalized pseudo pressure should be plotted versus the time function as shown in Fig. 5d.

The RTA equations use t _BDF and m _LF to characterize the SRV parameters. For oil wells with constant production rate, the SRV permeability and hydraulic fracture size can be estimated as follows (Rasdi and Chu 2012):

$$K_{\text{SRV}} = \frac{{79.01 \times \varphi_{\text{SRV}} \times \mu_{\text{o}} \times C_{\text{t}} \times Y_{e}^{2} }}{{t_{\text{BDF}} }}$$

(3)

$$X_{\text{f}} = \frac{{19.9 \times B_{\text{o}} }}{{n \times h \times m_{\text{LF}} }}\sqrt {\frac{\mu }{{k_{\text{SRV}} \times \varphi_{\text{SRV}} \times C_{\text{t}} }}}$$

(4)

For constant production rate in gas wells, the following equations have been proposed (Ibrahim et al. 2006):

$$\sqrt k \times A_{\text{c}} = \frac{803.2 \, \times T}{{m_{\text{LF}} \sqrt {\varphi_{\text{SRV}} \times \mu \times C_{\text{t}} } }}$$

(5)

$$A = \frac{90.36 \, \times T}{{\varphi_{\text{SRV}} \times \mu \times C_{\text{t}} }}\left( {\frac{{\sqrt {t_{\text{BDF}} } }}{{m_{\text{LF}} \times h}}} \right)$$

(6)

By combining the Eqs. 1 and 2 with the Eqs. 5 and 6, the SRV permeability and hydraulic fracture size can be estimated as follows:

$$K_{\text{SRV}} = \frac{{79.01 \times \mu_{\text{g}} \times \varphi_{\text{SRV}} \times C_{\text{t}} \times Y_{e}^{2} }}{{t_{\text{BDF}} }}$$

(7)

$$X_{\text{f}} = \frac{{ \, \sqrt {t_{\text{BDF}} } }}{{m_{\text{LF}} \times Y_{e} }}\frac{22.59T}{{n \, \times h \, \times \mu_{\text{g}} \times \varphi_{\text{SRV}} \times C_{\text{t}} }}$$

(8)

In the above equations, P is pressure (psia), t is time (days), Q _o is oil flow rate (STBD), Q _g is gas flow rate (MSCFD), B is formation volume factor, h is reservoir thickness (ft), µ is viscosity (cp), φ _SRV is the effective average porosity of the porous media in SRV that contributes to the flow (fraction), C _t is total compressibility, Y _e is distance to the boundary (optimistically, Y _e is half distance between each two adjacent hydraulic fractures), L is horizontal well length (ft), K _SRV is permeability of the stimulated reservoir volume, T is reservoir temperature (R), and n is number of the hydraulic fracturing stages.

The RTA method requires recording of surface production rates and bottom-hole pressure data. However, if only the well-head pressure data are available instead of bottom-hole pressure data, then WHP data should be converted to BHP using multi-phase flow well model correlations, and then be input into the RTA models. RTA can practically be used in multi-fractured shale reservoirs to characterize the SRV parameters.

Pressure buildup analysis (PBA) for multi-fractured shale reservoirs

In well test analysis of shale reservoirs, the pressure transient data and the derivatives should be plotted on the Log–Log diagnostic plot: d(p)/d(t ^0.5) as linear flow derivative, d(p)/d(t ^0.36) as elliptical flow derivative and d(p)/d(ln[t]) as radial flow derivative (see the “Appendix A” for more details). The plot is used to identify the pressure derivative values for infinite acting linear flow, elliptical flow and radial flow regimes (m _RF from zero slope line on radial flow derivative, m_Ell from zero slope line on elliptical flow derivative and m _LF from zero slope line on linear derivative) as shown in Fig. 6 (Arevalo et al. 2002; Martinez et al. 2012). If the test duration is short, then on the Log–Log diagnostic plot only the linear flow regime might be observed, and if the testing time is long enough, then both the linear and elliptical flow might be observed. For the PBA method, the pressure transient data before the effect of the early-time boundary-dominated flow effect are used for SRV characterization depending on the detected flow regimes.

Fig. 6

Well test analysis using pressure derivative on standard Log–Log diagnostic plot

The linear flow and elliptical flow regimes are both function of K _SRV and X _f, and combining the solutions of the diffusivity equation for linear and elliptical flow regimes and solving the two non-linear equations simultaneously can provide the two unknowns K _SRV and X _f. The solution of the diffusivity equation for infinite acting elliptical flow as function of elliptical flow regime slope, m _Ell, has been proposed for horizontal oil and gas wells (Martinez et al. 2012). The modified and re-derived solution of elliptical flow equation and linear flow equation for multi-fractured horizontal wells are as follows:

$${\text{For Elliptical flow:}}\,\,X_{\text{f}} \times K_{\text{SRV}}^{0.89} = \frac{{20.37 \times \mu^{0.89} }}{{ \varphi_{\text{SRV}}^{0.5} \times C_{\text{t}}^{0.5} }}\left( {\frac{ q \times B}{{ h \times n \times \, m_{\text{Ell}} }}} \right)^{1.39}$$

(9)

$${\text{For linear flow:}}\,\,K_{\text{SRV}} \times X_{\text{f}}^{2} = \left( {\frac{4.06 q B}{{m_{\text{LF}} h n \, }}} \right)^{2} \frac{\mu }{{\varphi_{\text{SRV}} \times C_{\text{t}} }}$$

(10)

Integrating the above two Eqs. 9 and 10 can provide the two unknowns X _f and K _SRV for an oil well in shale reservoirs (assuming that the effective average porosity of SRV to be known).

For gas wells and using the pseudo pressure in well test analysis, the following equations can provide fracture size and SRV permeability:

$${\text{For Elliptical flow:}}\,\,X_{\text{f}} \times K_{\text{SRV}}^{0.89} = \frac{573}{{\varphi_{\text{SRV}}^{0.5} \times (\mu \times C_{\text{t}} )^{0.5} }}\left( {\frac{q \times T}{{h \times \, n \, \times m_{\text{Ell}} }}} \right)^{1.39}$$

(11)

$${\text{For linear flow:}}\,\,K_{\text{SRV}} \times X_{\text{f}}^{2} = \left( {\frac{40.99 \times q \times T}{{ h \times n \times m_{\text{LF}} }}} \right)^{2} \frac{1}{{ \, \varphi_{\text{SRV}} \times \mu \times C_{\text{t}} }}$$

(12)

In the above equations, P is pressure (psia), t is time (h), q is oil flow rate (STBD), B is formation volume factor, h is reservoir thickness (ft), µ is viscosity (cp), φ _SRV is the effective average porosity of SRV (fraction) that may be dominated by matrix porosity effect since the fractures may have very small porosity, C _t is total compressibility, n is number of hydraulic fractures, and K _SRV is SRV average permeability that may be mainly controlled by permeability of the fractures. Based on the analytical derivations, the value of m _LF can be a good indicator of well deliverability. The production data for the first few months can be displayed on RTA plots to evaluate well deliverability of producing wells in a field.

For multi-fractured wells in unconventional low-permeability gas reservoirs, only the linear flow regime may be observed on the diagnostic plots (testing time is not long enough to have radial flow regime detected). To get some estimates of the SRV parameters, one can predict a theoretical late-time radial flow regime inside the SRV using advanced methods such as the second derivative of transient pressure, to integrate the theoretical radial flow equation with the linear flow equation, and solve the two equations for the two unknowns with some uncertainties (Bahrami and Siavoshi 2013).

It should be noted that the above simplified equations do not take into account the changing gas viscosity and gas compressibility with the use of pseudo time, and they are based on single-phase flow. To get more accurate well test analysis results, gas slippage effect with pseudo time and pseudo pressure and also multi-phase parameters can be considered in the analytical approach of well test data analysis.

Uncertainties of SRV characterization using analytical methods

The main advantage of RTA method is that in RTA, using just WHP and Q data which can always be recorded and available during production, the SRV can be characterized. However, the RTA equations may have some uncertainties as well. The disadvantage of RTA method is that the early-time data specially the linear flow time period may be affected by well clean-up period, when oil and/or gas are produced with water and fracturing fluids. This causes the early-time linear flow data points on RTA plot to be scattered, and therefore m _LF cannot be identified very accurately. In other words, m _LF on RTA plot may not be the actual representative of the fracture performance. On RTA plots, the data points may also be scattered because of the changes in well conditions during production (well head, choke size, liquid loading in wellbore, etc.). These affect RTA plots and calculation of slope of the lines. Also if the effective number of producing fractures (n) is not known, it makes uncertainties to be more. Running a production log is required to identify the effective number of hydraulic fractures, and improve reliability of RTA results.

The main advantage of pressure buildup test data analysis is that the flow rate is constant during the test (Q = 0); therefore, the data points are significantly less scattered compared to the data on RTA plots, and m _LF can be identified more accurately using PBA plots. The accurate estimation of m _LF is very important, as it is an indicator of the well’s future production performance. Another advantage of PBA is that K _SRV is calculated independent from Y _e (that maybe unknown), and therefore the calculation of X _f will be more reliable. The uncertainties associated with the PBA method are when only a linear flow regime is observed on the diagnostic plots (one equation with two unknowns). It should be noted that the units of m _LF in RTA and PBA equations are different. Use m _LF,RTA = 4.9/Q × m _LF,PBA to convert m _LF from RTA units to m _LF from PBA units.

RTA equations are based on assuming Y _e  = L/n/2 (i.e., the reservoir volume around the horizontal well between each two fracturing stages, being fully stimulated). If the actual Y _e is smaller, then RTA underestimates the X _f value. Also the RTA method is based on assuming the whole SRV being productive shale with 100 % net volume, whereas in SRV there is productive net shale volume, as well as non-productive shale volume, and in reality, NTG volume may not be 100 %.

Also SRV permeability is not uniform and it is higher near the wellbore (larger fractures), and it is lower away from wellbore (smaller fractures). Using the analytical methods to estimate SRV parameters, it assumes a homogeneous single-porosity system and a fully stimulated pore volume with 100 % productive shale (optimistic assumption), which may result in under-estimation of hydraulic fracture size.

Therefore, in designing the well spacing based on the calculated X _f, the actual well spacing should be considered larger than the one determined from RTA.

The RTA and PBA methods both have different advantages and also uncertainties and, therefore, integrating the methods can provide more accurate characterization of SRV parameters. The proposed methodology is as follows:

• From RTA diagnostic plot, estimate t _BDF.

• From PBA Log–Log diagnostic plot, estimate m _LF and m _Ell.

• To estimate X _f and K _SRV (2 unknowns, 2 equations) for oil wells, use the values of m _LF and m _Ell, and integrate Eqs. 9 and 10. For gas wells, integrate Eqs. 11 and 12.

• To estimate X _f, K _SRV and Y _e (3 unknowns, 3 equations) for oil wells, use the values of t _BDF, m _LF and m _Ell, and integrate Eqs. 3, 9 and 10. For gas wells, integrate Eqs. 7, 11 and 12.

To examine accuracy of the proposed method for SRV characterization, a simple reservoir simulation model with one hydraulic fracture in a closed system (equivalent to one fractured stage in a multi-stage fractured well) is built and run using typical fractured shale reservoir characteristics. The input parameters into the SRV model (a single-porosity system) have been shown in Fig. 7 and Table 1. The model was run for production period of 1000 h with flow rate of 300 MSCFD, followed by 1000 h pressure buildup. Then RTA plots and equations were used to analyze the pressure drawdown data, and PBA plots and equations were used to analyze the pressure buildup data.

Fig. 7

SRV reservoir simulation model for a shale gas reservoir (assuming single-porosity SRV)

Table 1 Reservoir simulation model input data for RTA and PBA evaluation in the shale gas reservoir

The RTA results for the numerically generated data are shown in Fig. 8, and PBA results in Fig. 9. The results indicate that the m _LF value calculated from both RTA and PBA methods are in good agreement, confirming reliability of the proposed equations. The calculation results for SRV parameters are reported in Table 2, which indicate that the proposed equations provide reasonably good results (average error around 10 %) for the SRV characteristics (considering the fact that the simplified analytical equations have been used to analyze the numerically generated data). In a real case, since production rate during pressure buildup test is constant (Q = 0), PBA may provide slightly more accurate results than RTA; however, due to economical reasons, pressure buildup tests are not common as it required the wells not to produce, but production data are always available to apply RTA method.

Fig. 8

RTA analysis on reservoir simulation results

Fig. 9

PBA analysis on reservoir simulation results

Table 2 Comparison of RTA and PBA results (assuming single-porosity SRV)

It should be noted that SRV is a dual-porosity and dual-permeability system, but the RTA and PBA equations are based on single-porosity system. Using the matrix porosity in RTA calculations as the effective SRV porosity, it assumes a single-porosity system and a fully stimulated pore volume, in which the volume occupied by hydraulic fractures is equal to porosity of matrix (this is an optimistic assumption, since fracture porosity is significantly less than matrix porosity). The assumption may result in under-estimation of hydraulic fracture size, and therefore RTA results may be optimistic. In this paper, reservoir simulation and history matching approach in a dual-porosity model are presented to characterize SRV more accurately.

Characterizing SRV using dual-porosity simulation model

The RTA and PBA equations are based on single-porosity models, whereas the SRV in multi-fractured shale reservoirs is actually a dual-porosity system, and the stimulated rock volume is a random network of untreated shale matrix blocks and fracture planes. Characterization of a dual-porosity SRV in multi-fractured shale reservoirs generally includes estimating the dynamic parameters such as average SRV permeability and hydraulic fracture size.

Well test analysis of multi-fractured shale reservoirs using dual-porosity concept is challenging and may not be practical due to the extensive wellbore storage effect in a long fractured wellbore, heterogeneity of the reservoir, and complexities in the dual-porosity stimulated rock volume (Restrepo and Tiab 2009), and therefore conventional well test analysis for dual-porosity behavior using interporosity flow coefficient (λ) and fracture storativity ratio (ω) may not be meaningful.

The main input parameters that are required to model fluid flow in a fractured system are fracture permeability, fracture compressibility, fracture porosity, shape factor, and the productive shale net volume in SRV (NTG_shale). Shape factor (δ) can be defined for Kazemi model, as a function of matrix block size (a) that can be simplified to δ = 4/a ² (Saeedi 2012).

Fracture compressibility (C _f) in dual-porosity systems might be 1–100-folds higher than matrix compressibility. Fracture compressibility can be estimated from the following equation (Tiab et al. 2006):

$$C_{\text{f}} = \frac{{1 - (k/k_{i} )^{2/3} }}{\Delta P}$$

(13)

where K _i is well test permeability at initial reservoir pressure, K is well test permeability at the current reservoir pressure (permeability from RTA or PBA), and ΔP is pressure depletion in the system.

For characterizing fracture porosity (φ _f), fracture opening (b) and matrix block size (or fracture spacing: a), processing of image log data if it is an open-hole well can be used (Dashti et al. 2009; Luthi 1990). However, in multi-fractured cased-hole wells, logging applications for this purpose are very limited and running fracture characterization image logs may not be practical in fractured cased-hole wells. The alternative method is to use history matching approach and tuning the values to estimate the fracture parameters φ _f and δ.

Permeability of fractures in SRV can be estimated from the following equation based on Kazemi model (Bahrami et al. 2013):

$$K_{\text{f,actual}} = K_{\text{welltest}} /\varphi_{\text{f}} = K_{\text{welltest}} \times \frac{a}{b}$$

(14)

In dual-porosity reservoir simulation approach, to reduce the simulation convergence issues and improve the run time, the actual size of fracture grids (h _f,actual = b) are increased to be equal to matrix grid size (h _f,adjusted = L), and then permeability of the enlarged fractures are adjusted (reduced) to the new equivalent size of the fractures that results in the same fracture productivity (K _f,actual × h _f,actual = K _f,DP × h _f,adjusted). For a dual-porosity simulation model, Eq. 14 for fracture permeability can be written as follows:

$$K_{{{\text{f}},{\text{DP}}}} = K_{\text{welltest}} \times \frac{a}{L}$$

(15)

In the above equations, K _f,actual is the actual intrinsic permeability of fractures, K _f,DP is the equivalent fracture permeability for dual-porosity reservoir simulation model (permeability for the fracture grids), K _{well test} is average well test permeability (from RTA or PBA), b is average fracture aperture, a is average matrix block size, and L is average grid size in the SRV section of the simulation model.

The downhole stresses applied from different directions to the formation rock can control aperture (and, therefore, permeability) of the hydraulically created fractures. The fractures that are perpendicular to the minimum stress direction may have significantly better permeability than the fractures perpendicular to the maximum stress direction. The permeability estimated from RTA or PBA is equivalent to SRV K _average, the average permeability in the SRV model (K _average = K ^1/3 _x  × K ^1/3 _y  × K ^1/3 _z ).

To characterize SRV, reservoir simulation and history matching can be done using dual-porosity dual-permeability model. The reservoir model should be built considering that the given dual-porosity SRV volume is surrounded by the untreated single-porosity rock. Then the cumulative volume of injected water, oil production, water production, gas production, and flowing bottom-hole pressure should all be matched during history matched using the matching parameters such as SRV size and SRV permeability. The history match is achieved when the correct values for matrix and fractures parameters in the SRV are used in the reservoir model.

Field example: Eagle Ford Shale

The static and dynamic data from some multi-fractured wells in Eagle Ford shale are analyzed to characterize SRV in the reservoir. The typical petrophysical data for the shale reservoir are shown in Fig. 10: Gamma Ray versus CGR, log water saturation, neutron porosity, density porosity and corrected porosity. In shale intervals due to the bound water in the shale, porosity from Neutron Log is affected and it significantly overestimates the effective porosity, compared to density porosity. Over a shale interval with negligible TOC, the shale lithology effect on density log is not significant and density porosity should be the corrected porosity, but when TOC is significant, then density log readings are affected by presence of Kerogen. To calculate the effective porosity, TOC should be calculated first, and then density porosity log should be corrected based on that accordingly (the actual porosity in an organic-rich shale intervals is less than density porosity as shown in Fig. 10).

Fig. 10

Typical petrophysical characteristics of the shale reservoir

Typical core data have shown matrix permeability of 1E−6 md. For well test analysis, some wells with pressure and rate data available are selected to guess-estimate reservoir characteristics, and then reservoir simulation and history matching are used to characterize the reservoir as dual-porosity system, and therefore perform more accurate production forecast from the multi-fractured shale reservoir.

PBA for a shale gas multi-fractured horizontal well

Pressure buildup test data from a hydraulically fractured horizontal well in a shale gas field were analyzed to estimate SRV permeability and the average hydraulic fracture size. As shown in Fig. 11, the test duration is not long enough to reach radial flow regime, and analysis of the well test data have uncertainties using the conventional methods.

Fig. 11

Pressure buildup analysis for multi-fractured shale gas well-G1

Using the diagnostic plot shown in Fig. 11, the linear and elliptical flow regimes are both detected, and therefore the proposed well test analysis method can be used based on linear flow (LF) derivative and elliptical flow (EF) derivative. By integrating the diffusivity equation solution for the two reservoir flow regimes, the two unknowns K and X _f are calculated (Eqs. 11, 12): SRV permeability of 0.0005 mD and hydraulic fracture half-length of 48 ft.

RTA for shale gas and shale oil multi-fractured horizontal wells

The rate and pressure transient data are studied for two multi-fractured wells, one in a shale oil reservoir (well O1) and one in a shale gas reservoir (well G2), to show applications of RTA in characterizing SRV in multi-fractured wells.

The plots and results of RTA in the gas well G-2 are shown in Fig. 12, which shows determination of m_LF and t_BDF from the RTA plots. The values are input in Eqs. 7 and 8, and the results showed average K _SRV = 0.002 md and X _f = 94 ft.

Fig. 12

RTA in multi-fractured shale gas well-G2

The plots and results of RTA in the oil well O-2 are shown in Fig. 13, which shows determination of m _LF and t _BDF from the RTA plots. The values are input in Eqs. 7 and 8, and the results showed average K _SRV = 0.006 md and X _f = 70 ft.

Fig. 13

RTA in multi-fractured shale oil well-O1

Characterizing multi-fractured shale oil reservoir using dual-porosity simulation model

The main objective of shale gas reservoir simulation and history matching is to build a representative simulation model that can provide a reliable production forecast. For a multi-fractured shale oil well in Eagle Ford Shale, the dual-porosity reservoir simulation model was built (to model the fracturing process in the simulation software, transmissibility of the grids that their pressure goes above rock breakdown pressure during water injection are increased to allow water to flow into those simulation cells). Oil production rate was selected as simulation control parameter, and then the well injectivity and SRV parameters were tuned to achieve a good history match for gas production rate, water production rate, well flowing bottom-hole pressure, and cumulative injected water during fracturing. The input data into the simulation model are reported in Table 3, and the history match reservoir simulation results are presented in Fig. 14. A satisfactory history match could be achieved by considering fracturing fluid loss of 54 % (history match of the other wells in this field also showed fluid loss), which could probably be loss of fluid into some non-productive shale zones or fluid loss behind casing through some micro-channels between cement, casing and formation (in other words, the SRV could ideally–theoretically be larger and production rates be higher, if there was no frac fluid loss). Table 4 shows the SRV parameters that provided a good history match, as a reliable model to be used in production forecasting for the multi-fractured shale oil well.

Table 3 Input data into the reservoir simulation model of the multi-fractured SRV

Fig. 14

Characterizing multi-staged fractured shale oil using reservoir simulation and history matching (SENSOR software)

Table 4 Reservoir simulation and history match results for the multi-fractured SRV

Conclusions

• Rate transient analysis (RTA) and pressure buildup analysis (PBA) can practically be used to have estimations of the stimulated reservoir volume (SRV) parameters in shale reservoirs.

• In RTA method, the slope of the linear flow regime data (m _LF) and the time at which boundary-dominated flow starts (t _BDF) are used for K _SRV and X _f estimation.

• In PBA method, integration of diffusivity equations solutions for linear and elliptical flow regimes can provide estimation of SRV characteristics. The values of m _Ell and m _LF can be determined, respectively, from zero slope line on elliptical flow derivative and zero slope line on linear flow derivative.

• The value of m _LF can be a good indicator of well deliverability. The m _LF from PBA may be more reliable than the value of m _LF from RTA, since during a pressure buildup test, production rate is constant (Q = 0) and, therefore, the data quality is better. However, in terms of data availability in producing wells, most wells have production data for RTA, but few wells may have the pressure buildup data required for PBA.

• Integration of rate transient analysis and pressure buildup analysis methods can reduce uncertainties in SRV characterization.

• Reservoir simulation and history matching using dual-porosity SRV model is more reliable method for SRV characterization, compared with the analytical methods.

Appendix A: General forms of fluid flow equations for different flow regimes

(Bahrami et al. 2013; Martinez et al. 2012; Kappa Engineering 2012)

Wellbore storage effect

$$\begin{aligned} \Delta P & = c\,\Delta t \\ {\text{Log}}\left( {\Delta P} \right) & = \left( { + 1} \right){\text{Log}}\left[ {\Delta t} \right] + {\text{Log}}\left( c \right) \\ {\text{Log}}\left[ {{\text{d}}\left( {\Delta P} \right)/{\text{d}}\left( {\Delta t} \right)} \right] & = 0\;{\text{Log}}\left[ {\Delta t} \right] + {\text{Log}}\left( c \right)\,\,\,\,{\text{Log}}\left[ {{\text{d}}\left( {\Delta P} \right)/{\text{d}}\left( {{ \ln }\left( {\Delta t} \right)} \right)} \right] = 1{\text{Log}}\left[ {\Delta t} \right] + {\text{Log}}\left( c \right) \\ \end{aligned}$$

Radial flow equation (field unit)

$$\begin{aligned} \Delta P & = m_{\text{RF}} \times {\text{Log}}\left[ {\Delta t} \right] + b_{\text{R}} \\ \frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {{ \ln }\,\Delta t} \right)}} & = 2.3m \\ {\text{Log}}\left[ {\frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {{ \ln }\Delta t} \right)}}} \right] & = 0\log \left[ {\Delta t} \right] + \log \left[ {2.3m} \right] \to K = \frac{{162.6 \times Q \times \mu \times B_{\text{o}} }}{{\left( {2.3 \times m_{\text{RF}} } \right) \times h}} \\ \end{aligned}$$

For pressure drown down test:

$$S = 1.1513 \times \left[ {\frac{{\Delta P_{\text{RF}} }}{{2.3 \times m_{\text{RF}} }} - \log \left( {\Delta t_{\text{RF}} } \right) - \log \left( {\frac{k}{{\varphi \mu c_{\text{t}} r_{\text{w}}^{2} }}} \right) + 3.23} \right]$$

For pressure buildup test:

$$S = 1.1513 \times \bigg[ {\frac{{\Delta P_{{{\text{RF}}}} }}{{2.3 \times m_{{{\text{RF}}}} }} + \log \left( {\frac{{t_{{\text{p}}} + \Delta t_{{{\text{RF}}}} }}{{\Delta t_{{{\text{RF}}}} \left( {1 + t_{{\text{p}}} } \right)}}} \right) + \log \left( {\frac{{t_{p} + 1}}{{t_{p} }}} \right) - \log \left( {\frac{K}{{\varphi \mu c_{{\text{t}}} r_{{\text{w}}}^{2} }}} \right) + 3.23} \bigg]$$

Linear flow equation (field unit)

$$\begin{aligned} \Delta P & = m_{\text{LF}} \times [\Delta t]^{1/2} + b_{\text{L}} \\ \frac{{{\text{d}}(\Delta P)}}{{{\text{d}}(\Delta^{1/2} )}} & = m_{\text{LF}} \to {\text{Log}}\left[ {\frac{{{\text{d}}(\Delta P)}}{{{\text{d}}(\Delta^{1/2} )}}} \right] = 0\log [\Delta t] + \log [m_{\text{LF}} ] \\ \end{aligned}$$

$$\begin{array}{*{20}c} {} & {{\text{Hydraulically}}\,{\text{fractured}}\,{\text{well}}} & {{\text{Horizontal}}\,{\text{well}}} \\ {{\text{Oil}}\,{\text{wells:}}} & {K \times X_{\text{f}}^{2} = \left( {\frac{4.06\,qB}{{m_{\text{LF}} h}}} \right)^{2} \frac{\mu }{{\varphi C_{\text{t}} }}} & {K \times \left( {\frac{L}{2}} \right)^{2} = \left( {\frac{4.06\,qB}{{m_{\text{LF}} h}}} \right)^{2} \frac{\mu }{{\varphi C_{\text{t}} }}} \\ {{\text{Gas}}\,{\text{wells:}}} & {K \times X_{\text{f}}^{2} = \left( {\frac{40.99\, \times\, q\, \times\, T}{{h\, \times\, n\, \times\, m_{\text{LF}} }}} \right)^{2} \frac{1}{{\varphi \times \mu \times C_{\text{t}} }}} & {K \times \left( {\frac{L}{2}} \right)^{2} = \left( {\frac{40.99\, \times\, q \times\, T}{{h\, \times\, n\, \times\, m_{\text{LF}} }}} \right)^{2} \frac{1}{{\varphi\, \times\, \mu\, \times C_{\text{t}} }}} \\ \end{array}$$

Elliptical flow equation (field unit)

$$\begin{aligned} \Delta P & = m_{\text{Ell}} \times \left[ {\Delta t} \right]^{0.36} + b_{\text{Ell}} \\ \frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {\Delta t^{0.36} } \right)}} & = m_{\text{Ell}} \to {\text{Log}}\left[ {\frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {\Delta t^{0.36} } \right)}}} \right] = 0\log [\Delta t] + \log [m_{\text{Ell}} ] \\ \end{aligned}$$

$$\begin{array}{*{20}c} {} & {{\text{Hydraulically}}\,{\text{fractured}}\,{\text{well}}} & {{\text{Horizontal}}\,{\text{well}}} \\ {{\text{Oil}}\,{\text{wells:}}} & {K \times X_{\text{f}}^{2} = \left( {\frac{4.06qB}{{m_{\text{LF}} h}}} \right)^{2} \frac{\mu }{{\varphi C_{\text{t}} }}} & {K \times \left( {\frac{L}{2}} \right)^{2} = \left( {\frac{4.06qB}{{m_{\text{LF}} h}}} \right)^{2} \frac{\mu }{{\varphi C_{\text{t}} }}} \\ {{\text{Gas}}\,{\text{wells:}}} & {K \times X_{\text{f}}^{2} = \left( {\frac{40.99 \times q \times T}{{h \times n \times m_{\text{LF}} }}} \right)^{2} \frac{1}{{\varphi \times \mu \times C_{\text{t}} }}} & {K \times \left( {\frac{L}{2}} \right)^{2} = \left( {\frac{40.99 \times q \times T}{{h \times n \times m_{\text{LF}} }}} \right)^{2} \frac{1}{{\varphi \times \mu \times C_{\text{t}} }}} \\ \end{array}$$

Elliptical flow equation (field unit)

$$\begin{aligned} \Delta P & = m_{\text{Ell}} \times \left[ {\Delta t} \right]^{0.36} +\,\, b_{\text{Ell}} \\ \frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {\Delta t^{0.36} } \right)}} & = m_{\text{Ell}} \to {\text{Log}}\left[ {\frac{{{\text{d}}\left( {\Delta P} \right)}}{{{\text{d}}\left( {\Delta t^{0.36} } \right)}}} \right] = 0\log [\Delta t] + \log [m_{\text{Ell}} ] \\ \end{aligned}$$

$$\begin{array}{*{20}c} {} & {{\text{Hydraulically}}\;{\text{fractured}}\;{\text{well}}} & {{\text{Horizontal}}\;{\text{well}}} \\ {{\text{Oil}}\,{\text{wells:}}} & {X_{\text{f}}\, \times\, K^{0.89} = \frac{{20.37\, \times\, \mu^{0.89} }}{{(\varphi C_{\text{t}} )^{0.5} }}\left( {\frac{q\, \times\, B}{{h\, \times\, m_{\text{Ell}} }}} \right)^{1.39} } & {K^{0.89}\, \times\, \frac{L}{2} = \frac{{20.37 \,\times\, \mu^{0.89} }}{{(\varphi C_{\text{t}} )^{0.5} }}\left( {\frac{q\, \times\, B}{{h\, \times\, m_{\text{Ell}} }}} \right)^{1.39} } \\ {{\text{Gas}}\,{\text{wells:}}} & {X_{\text{f}}\, \times\, K^{0.89} = \frac{573}{{\varphi_{\text{SRV}}^{0.5}\, \times\, (\mu\, \times\, C_{\text{t}} )^{0.5} }}\left( {\frac{q\, \times\, T}{{h\, \times\, n\, \times\, m_{\text{Ell}} }}} \right)^{1.39} } & {\frac{L}{2} \,\times\, K^{0.89} = \frac{573}{{\varphi_{\text{SRV}}^{0.5}\, \times\, (\mu\, \times\, C_{\text{t}} )^{0.5} }}\left( {\frac{q\, \times\, T}{{h\, \times\, n\, \times\, m_{\text{Ell}} }}} \right)^{1.39} } \\ \end{array}$$

In the above equations, P is pressure (psia), t is time (h), q is production rate (oil: STBD, gas: MSCFD), h is reservoir thickness (ft), B is formation volume factor, μ is viscosity (cp), C _t is total compressibility, φ is effective average porosity (fraction), K is permeability of the stimulated rock volume, T is reservoir temperature (R), m _RF is pressure derivative value for infinite acting radial flow, m _LF is pressure derivative value for infinite acting linear flow, and m _EF is pressure derivative value for infinite acting elliptical flow. For multi-fractured horizontal wells, n is total number of fractures and h is total reservoir thickness, but for multi-fractured vertical wells, n = l for h as total reservoir thickness of all the fractured layers.Time functions for pressure derivative calculation in a pressure buildup test:

$${\text{Radial}}\,{\text{flow:}}\,{\text{Log}}[(t_{\text{p}} + \Delta t)/\Delta t],\;{\text{Linear}}\,{\text{flow:}}\;(t_{\text{p}} + \Delta t)^{1/2} - \Delta t^{1/2} ,\,{\text{Elliptical}}\,{\text{flow}}:(t_{\text{p}} + \Delta t)^{0.36} - \Delta t^{0.36}$$

Well test analysis concepts for non-fractured wells

Well test analysis concepts for hydraulically fractured wells