Download PDF

New explicit correlation for the compressibility factor of natural gas: linearized z-factor isotherms

  • Lateef A. Kareem
  • Tajudeen M. Iwalewa
  • Muhammad Al-Marhoun
Open Access
Original Paper - Production Engineering
First Online:
Received:
Accepted:

DOI: 10.1007/s13202-015-0209-3

Cite this article as:
Kareem, L.A., Iwalewa, T.M. & Al-Marhoun, M. J Petrol Explor Prod Technol (2016) 6: 481. doi:10.1007/s13202-015-0209-3

Abstract

The compressibility factor (z-factor) of gases is a thermodynamic property used to account for the deviation of real gas behavior from that of an ideal gas. Correlations based on the equation of state are often implicit, because they require iteration and are computationally expensive. A number of explicit correlations have been derived to enhance simplicity; however, no single explicit correlation has been developed for the full range of pseudo-reduced temperatures \(\left( {1.05 \le T_{pr} \le 3} \right)\) and pseudo-reduced pressures \(\left( {0.2 \le P_{pr} \le 15} \right)\), which represents a significant research gap. This work presents a new z-factor correlation that can be expressed in linear form. On the basis of Hall and Yarborough’s implicit correlation, we developed the new correlation from 5346 experimental data points extracted from 5940 data points published in the SPE natural gas reservoir engineering textbook and created a linear z-factor chart for a full range of pseudo-reduced temperatures \((1.15 \le T_{pr} \le 3)\) and pseudo-reduced pressures \((0.2 \le P_{pr} \le 15)\).

Keywords

Z-factor Explicit correlation Reduced temperature Reduced pressure Natural gas 

List of symbols

P

Pressure (psi)

\(P_{pc}\)

Pseudo-critical pressure

\(P_{pr}\)

Pseudo-reduced pressure

T

Temperature (R)

\(T_{pc}\)

Pseudo-critical temperature (R)

\(T_{pr}\)

Pseudo-reduced temperature

\(P_{pc}\)

Pseudo-critical pressure (psi)

\(P_{pr}\)

Pseudo-reduced pressure

\(v\)

Initial guess for iteration process

Y

Pseudo-reduced density

z-factor

Compressibility factor

Introduction

The compressibility factor (z-factor) of gases is used to correct the volume of gas estimated from the ideal gas equation to the actual value. It is required in all calculations involving natural gases.

The z-factor is the ratio of the volume occupied by a given amount of a gas to the volume occupied by the same amount of an ideal gas:
$$z = \frac{{V_{\text{actual}} }}{{V_{\text{ideal}} }}$$
(1)
Substituting for \(V_{\text{ideal}}\) in the ideal gas equation
$$PV_{\text{actual}} = znRT$$
(2)

For generalization, the z-factor is expressed as a function of pseudo-reduced temperature and pressure (Trube 1957; Dranchuk et al. 1971; Abou-kassem and Dranchuk 1975; Sutton 1985; Heidaryan et al. 2010).

Dranchuk et al. (1971) defined pseudo-reduced temperature and pressure as the ratio of temperature and pressure to the pseudo-critical temperature and pressure of natural gas, respectively:
$$T_{pr} = \frac{T}{{T_{pc} }} , \quad P_{pr} = \frac{P}{{P_{pc} }}$$
(3)
The pseudo-critical properties of gas are the molar abundance (mole fraction weighted) mean of the critical properties of the constituents of the natural gas:
$$T_{pc} = \mathop \sum \limits_{i = 1}^{n} y_{i} T_{ci} ,\quad P_{pc} = \mathop \sum \limits_{i = 1}^{n} y_{i} P_{ci}$$
(4)
As a function of specific gravity (air = 1.0), Sutton (1985) provides
$$T_{pc} = 169.2 + 349.5{{\gamma_{g} }} - 74.0\gamma_{g}^{2}$$
(5)
$$P_{pc} = 756.8 - 131.07\gamma_{g} - 3.6\gamma_{g}^{2}$$
(6)
A plot of 5346 data points covering a full range of pseudo-reduced temperatures \((1.15 \le T_{pr} \le 3)\) and pseudo-reduced pressures \((0.2 \le P_{pr} \le 15)\) is shown in Fig. 1
Fig. 1

Plot of experimental measurements of the z-factor

Implicit z-factor correlations

The three most popular correlations for calculating the z-factor are implicit. The three correlations, described in the following subsections, are well known for their accuracies, almost unit correlation of regression coefficients and low maximum errors.

Hall and Yarborough’s correlation (Trube 1957)

Hall and Yarborough’s correlation is a modification of the hard sphere Carnahan–Starling equation of state, with constants developed through regression, and 1500 data points extracted from Standing and Katz’s original z-factor chart, as shown in Fig. 2.
$$z = \frac{{A_{1} P_{pr} }}{y},$$
(7)
where y is the root of the following equation:
$$\begin{aligned} & - A_{1} P_{pr} + \frac{{y + y^{2} + y^{3} - y^{4} }}{{(1 - y)^{3} }} - A_{2} y^{2} + A_{3} y^{{A_{4} }} = 0 \\ & A_{1} = 0.06125te^{{ - 1.2(1 - t)^{2} }} ,\quad A_{2} = 14.76t - 9.76t^{2} + 4.58t^{3} , \\ & A_{3} = 90.7t - 242.2t^{2} + 42.4t^{3} ,\quad A_{4} = 2.18 + 2.82t, \quad t = \frac{1}{{T_{pr} }} \\ \end{aligned}$$
Fig. 2

Standing and Katz’s compressibility factor chart

Dranchuk and Abou-Kassem’s correlation (Abou-kassem and Dranchuk 1975)

This is an eleven-constant modification of the Benedict–Webb–Rubin equation of state. The constants were calculated using a regression method, with 1500 data points extracted from standing and Katz’s chart.
$$z = \frac{{0.27P_{pr} }}{{yT_{pr} }},$$
(8)
where y is the root of the following equation:
$$\begin{aligned} & \left[ {R_{5} y^{2} (1 + A_{11} y^{2} )e^{{( - A_{11} y^{2} )}} } \right] + R_{1} y - \frac{{R_{2} }}{y} + R_{3} y^{2} - R_{4} y^{5} + 1 = 0 \\ & R_{1} = A_{1} + \frac{{A_{2} }}{{T_{pr} }} + \frac{{A_{3} }}{{T_{pr}^{3} }} + \frac{{A_{4} }}{{T_{pr}^{4} }} + \frac{{A_{5} }}{{T_{pr}^{5} }}, \quad R_{2} = \frac{{0.27P_{pr} }}{{T_{pr} }} \\ & R_{3} = A_{6} + \frac{{A_{7} }}{{T_{pr} }} + \frac{{A_{8} }}{{T_{pr}^{2} }},\quad R_{4} = A_{9} \left( {\frac{{A_{7} }}{{T_{pr} }} + \frac{{A_{8} }}{{T_{pr}^{2} }}} \right), \quad R_{5} = \frac{{A_{10} }}{{T_{pr}^{3} }} \\ & A_{1} = 0.3265, \quad A_{2} = - 1.0700, \quad A_{3} = - 0.5339, \quad A_{4} = 0.01569, \\ & A_{5} = - 0.05165, \quad A_{6} = 0.5475, \quad A_{7} = 0.7361, \quad A_{8} = 0.1844, \\ & A_{9} = 0.1056, \quad A_{10} = 0.6134, \quad A_{11} = 0.7210 \\ \end{aligned}$$

Dranchuk, Purvis and Robinson’s Correlation (Dranchuk et al. 1971)

This is a further modification of the earlier obtained DAK correlation. The DPR has eight constants and requires less computational workload to obtain the z-factor.
$$z = \frac{{0.27P_{pr} }}{{yT_{pr} }},$$
(9)
where y is the root of the following equation:
$$\begin{aligned} & \left[ {T_{4} y^{2} (1 + A_{8} y^{2} )e^{{( - A_{8} y^{2} )}} } \right] + 1 + T_{1} y + T_{2} y^{2} + T_{3} y^{5} + \frac{{T_{5} }}{y} = 0 \\ & T_{1} = A_{1} + \frac{{A_{2} }}{{T_{pr} }} + \frac{{A_{3} }}{{T_{pr}^{3} }},\quad T_{2} = A_{4} + \frac{{A_{5} }}{{T_{pr} }}, \quad T_{3} = \frac{{A_{5} A_{6} }}{{T_{pr} }}, \quad T_{4} = \frac{{A_{7} }}{{T_{pr}^{3} }}, \quad T_{5} = \frac{{0.27P_{pr} }}{{T_{pr} }} \\ & A_{1} = 0.31506237, \quad A_{2} = - 1.04670990, \quad A_{3} = - 0.57832720, \quad A_{4} = 0.53530771, \\ & A_{5} = - 0.61232032, \quad A_{6} = - 0.10488813, \quad A_{7} = 0.68157001, \quad A_{8} = 0.68446549 \\ \end{aligned}$$

These correlations are effective; however, they do not converge (or converge on wrong pseudo-reduced density values) when the temperature of the systems is close to the critical temperature. In addition, they are computationally expensive. It is these limitations that necessitated the development of the current explicit correlations.

Explicit correlations

Explicit correlations do not require an iterative procedure. Therefore, they do not have the problem of convergence as opposed to implicit correlations. One of the best explicit correlations for evaluation of the z-factor was given by Beggs and Brills (1973). More recent ones are Heidaryan et al. (2010), Azizi et al. (2010) and Sanjari and Lay (2012) correlations. A short description of some of the explicit correlations is presented in the following subsections.

Brill and Beggs’ compressibility factor (1973)

$$z = A + \frac{1 - A}{{e^{B} }} + Cp_{pr}^{D} ,$$
where
$$\begin{aligned} A & = 1.39(T_{pr} - 0.92)^{0.5} - 0.36T_{pr} - 0.10, \\ B & = (0.62 - 0.23T_{pr} )p_{pr} + \left( {\frac{0.066}{{T_{pr} - 0.86}} - 0.037} \right)p_{pr}^{2} + \frac{{0.32p_{pr}^{2} }}{{10^{E} }} \\ C & = 0.132 - 0.32\log (T_{pr} ), \;D = 10^{F} , \\ E & = 9(T_{pr} - 1)\;{\text{and}}\; F = 0.3106 - 0.49T_{pr} + 0.1824T_{pr}^{2} \\ \end{aligned}$$

Heidaryan, Moghdasi and Rahimi’s Correlation

Heidaryan et al. (2010) developed a new explicit piecewise correlation using regression analysis of the z-factor experimental value for reduced pseudo-pressure of fewer and >3 (Table 1). The correlation has a total of 22 constants, with a discontinuity at \(P_{pr} = 3\) (Fig. 2) and correlation regression coefficient of 0.99,963.
$$z = \ln \left( {\frac{{A_{1} + A_{3} \ln (P_{pr} ) + \frac{{A_{5} }}{{T_{pr} }} + A_{7} \left( {\ln (P_{pr} )} \right)^{2} + \frac{{A_{9} }}{{T_{pr}^{2} }} + \frac{{A_{11} }}{{T_{pr} }}\ln (P_{pr} )}}{{1 + A_{2} \ln (P_{pr} ) + \frac{{A_{4} }}{{T_{pr} }} + A_{6} \left( {\ln (P_{pr} )} \right)^{2} + \frac{{A_{8} }}{{T_{pr}^{2} }} + \frac{{A_{10} }}{{T_{pr} }}\ln (P_{pr} )}}} \right)$$
(11)
Table 1

Constants of Heidaryan et al.’s correlation

 

Constants for \(P_{pr} \le 3\)

Constants for \(P_{pr} > 3\)

A1

2.827793

3.252838

A2

−4.688191 × 10−1

−1.306424 × 10−1

A3

−1.262288

6.449194 × 10−1

A4

−1.536524

−1.518028

A5

−4.535045

−5.391019

A6

6.895104 × 10−2

−1.379588 × 10−2

A7

1.903869 × 10−1

6.600633 × 10−2

A8

6.200089 × 10−1

6.120783 × 10−1

A9

1.838479

2.317431

A10

4.052367 × 10−1

1.632223 × 10−1

A11

1.073574

5.660595 × 10−1

For some petroleum engineering applications, it is often necessary to compute the derivative of z-factor with respect to pressure or temperature. A function that is discontinuous at a certain point is not differentiable at that point (O’Neil 2012). Therefore, the explicit correlation developed by Heidaryan et al. (2010) cannot be used to evaluate the derivative of the z-factor with respect to the pseudo-reduced pressure at \(P_{pr} = 3\) (Fig. 3).
Fig. 3

Heidaryan et al.’s (2010) correlation showing discontinuity at \(P_{pr} \le 3\)

Azizi, Behbahani and Isazadeh’s Correlation

Azizi et al. (2010) presented an explicit correlation with 20 constants for a reduced temperature range of \(1.1 \le T_{pr} \le 2\) and reduced pressure range of \(0.2 \le P_{pr} \le 11\). The correlation used 3038 data points within the given ranges.
$$z = A + \frac{B + C}{D + E},$$
(12)
where
$$\begin{aligned} A & = a T_{pr}^{2.16} + b P_{pr}^{1.028} + c P_{pr}^{1.58} T_{pr}^{ - 2.1} + d\ln \left( {T_{pr}^{ - 0.5} } \right) \\ B & = e + f T_{pr}^{2.4} + g P_{pr}^{1.56} + h P_{pr}^{0.124} T_{pr}^{3.033} \\ C & = i\ln \left( {T_{pr}^{ - 1.28} } \right) + j\ln \left( {T_{pr}^{1.37} } \right) + k\ln \left( {P_{pr} } \right) + l\ln \left( {P_{pr}^{2} } \right) + m\ln (P_{pr} )\ln (T_{pr} ) \\ D & = 1 + n T_{pr}^{5.55} + o P_{pr}^{0.68} T_{pr}^{0.33} \\ E & = p\ln \left( {T_{pr}^{1.18} } \right) + q\ln \left( {T_{pr}^{2.1} } \right) + r\ln (P_{pr} ) + s\ln \left( {P_{pr}^{2} } \right) + t\ln (P_{pr} )\ln (T_{pr} ) \\ \end{aligned}$$
$$\begin{aligned} a = 0.0373142485385592; \quad b = - 0.0140807151485369; \quad c = 0.0163263245387186; \quad d = - 0.0307776478819813; \quad e = 13843575480.943800; \quad f = - 16799138540.763700; \quad g = 1624178942.6497600; \quad h = 13702270281.086900; \quad i = - 41645509.896474600; \quad j = 237249967625.01300; \quad k = - 24449114791.1531;\quad l = 19357955749.3274; \quad m = - 126354717916.607;\quad n = 623705678.385784;\quad o = 17997651104.3330; \quad p = 151211393445.064;\quad q = 139474437997.172;\quad r = - 24233012984.0950; \quad s = 18938047327.5205;\quad t = - 141401620722.689; \end{aligned}$$

Sanjari and Nemati’s Correlation

Using 5844 data points, Sanjari and Lay (2012) developed an explicit correlation for the z-factor. This correlation, as with Heidaryan et al. (2010) correlation, has different constants for the values of \(P_{pr}\) below and above 3, but a total of 16 constants (Table 2). The procedure for calculating the z-factor is as follows:
$$z = 1 + A_{1} P_{pr} + A_{2} P_{pr}^{2} + \frac{{A_{3} P_{pr}^{{A_{4} }} }}{{T_{pr}^{{A_{5} }} }} + \frac{{A_{6} P_{pr}^{{(A_{4} + 1)}} }}{{T_{pr}^{{A_{7} }} }} + \frac{{A_{8} P_{pr}^{{(A_{4} + 2)}} }}{{T_{pr}^{{(A_{7} + 1)}} }}$$
(13)
Table 2

Constants of Sanjari and Lay’s correlation

 

Constants for \(P_{pr} \le 3\)

Constants for \(P_{pr} > 3\)

A1

0.007698

0.015642

A2

0.003839

0.000701

A3

−0.467212

2.341511

A4

1.018801

−0.657903

A5

3.805723

8.902112

A6

−0.087361

−1.136000

A7

7.138305

3.543614

A8

0.083440

0.134041

This correlation, however, is less efficient when compared with that of Heidaryan et al. (2010). Its regression correlation coefficient is 0.8757 and its error rate at a certain point can be as high as 90 per cent. For instance, the actual value of z from the experiment for a \(P_{pr}\) of 15 and a \(T_{pr}\) of 1.05 is 1.753, but this correlation gives a value of 3.3024. Therefore, the actual maximum error for this correlation is 104.3206 %.

To resolve the limitations in the application of the existing explicit correlations, a single correlation that is continuous over the entire range of pseudo-reduced pressure is required.

New explicit z-factor correlation

A new explicit z-factor is developed as a multi-stage correlation based on Hall and Yarborough’s implicit correlation. The implicit correlation was rearranged to return a value of y using an approximate value of z. The y-values on the right side of the expression were replaced by \(\left( {A_{1} P_{pr} /z} \right)\). Non-linear regression was performed using the derived model. The resulting correlation for reduced density is given in Eq. 15, while Eq. 14 provides an extra iteration to bring the results closer to those obtained by Hall and Yarborough. The constants for these two equations are shown in

Table 3. The z-factor chart shown in Fig. 4 was generated from this new correlation:
$$z = \frac{{ DP_{pr} (1 + y + y^{2} - y^{3} )}}{{(DP_{pr} + Ey^{2} - Fy^{G} )(1 - y)^{3} }}$$
(14)
$$y = \frac{{ DP_{pr} }}{{\left( {\frac{{1 + A^{2} }}{C} - \frac{{A^{2} B}}{{C^{3} }}} \right)}},$$
(15)
where
$$\begin{aligned} t & = \frac{1}{{T_{pr} }}, \\ A & = a_{1} te^{{a_{2} (1 - t)^{2} }} P_{pr} , \quad B = a_{3} t + a_{4} t^{2} + a_{5} t^{6} P_{pr}^{6} , \\ C & = a_{9} + a_{8} tP_{pr} + a_{7} t^{2} P_{pr}^{2} + a_{6} t^{3} P_{pr}^{3} \\ D & = a_{10} te^{{a_{11} (1 - t)^{2} }} , \quad E = a_{12} t + a_{13} t^{2} + a_{14} t^{3} , \\ F & = a_{15} t + a_{16} t^{2} + a_{17} t^{3} ,\quad G = a_{18} + a_{19} t \\ \end{aligned}$$
Table 3

Constants of the new correlation

Constants

a1

0.317842

a11

−1.966847

a2

0.382216

a12

21.0581

a3

−7.768354

a13

−27.0246

a4

14.290531

a14

16.23

a5

0.000002

a15

207.783

a6

−0.004693

a16

−488.161

a7

0.096254

a17

176.29

a8

0.166720

a18

1.88453

a9

0.966910

a19

3.05921

a10

0.063069

  
Fig. 4

Plot of z-factor generated using Eq. 14

Linearized z-factor isotherms

Given that the reduced temperature and pressure fall within \(1.15 \le T_{pr} \le 3\) and \(6 \le P_{pr} \le 15\), the first nine constants can be used to predict z with a correlation regression coefficient of 0.99899. For this range of pseudo-reduced properties, the simplified single-stage correlation of the z-factor is given by
$$z = \frac{{1 + A^{2} }}{C} - \frac{{A^{2} B}}{{C^{3} }}$$
(16)
A plot of Eq. 16 is shown in Fig. 5.
Fig. 5

Plot of z-factor generated using Eq. 16

A careful analysis of Eq. 16 shows that it can be rewritten in the following form:
$$zC = 1 + MP_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right)$$
(17)
The values of M are chosen to be a function of reduced temperature and a regression analysis performed to extend the applicability of Eq. 17 to cover the ranges \(1.15 \le T_{pr} \le 3\) and \(0.2 \le P_{pr} \le 15\). For this range of values of reduced temperature and pressure, M is given by
$$\begin{aligned} & M = m_{1} t^{2} e^{{m_{2} (1 - t)^{2} }} , \\ & m_{1} = 0.1009332,\quad m_{2} = 0.7773702 \\ \end{aligned}$$
It should be noted that B and C maintain the same definition as in Eq. 16. Hence, a graph of \(zC\) against \(P_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right)\) gives straight lines passing through the point \(\left( {P_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right) = 0, zC = 1} \right)\) with slopes M. A plot of the straight line form of the z-factor is shown in Fig. 6.
Fig. 6

Linear form z-factor chart using Eq. 17

Results and discussion

Figure 7 shows the cross plot of the z-factor from the new correlation against the measured values. The cross plots show that the plotted points fall on the unit slope line through the origin, which implies that the new correlation reproduces the measured values to a considerable degree of accuracy.
Fig. 7

Cross plot of correlation estimate against measured z-factor

Table 4 shows the statistical detail of the constants of the new correlation. The narrowness of the 95 per cent confidence interval is in agreement with the near-zero P-values. This implies that the probability that these values could have been developed by chance is negligible, which signifies that the new correlation is reliable (Wolberg 2006).
Table 4

Statistical detail of the constants of the new correlation

Constants

Estimated values

95 % confidence interval

P values

Correlation regression coefficient

a1

0.317842

{0.316999, 0.318686}

5.9718379920 × 10−5841

0.999864

a2

0.382216

{0.379011, 0.385422}

2.53091273354 × 10−2995

a3

−7.76835

{−7.95029, −7.58642}

4.4950402736 × 10−1007

a4

14.2905

{14.071, 814.5093}

5.1169104227 × 10−1710

a5

2.18363 × 10−6

{2.13411, 2.23314} × 10−6

8.8734666722 × 10−1053

a6

−0.00469257

{−0.00476861, −0.00461652}

4.4906844765 × 10−1604

a7

0.0962541

{0.095078, 0.0974301}

2.43824633475 × 10−2160

a8

0.16672

{0.160731, 0.17271}

2.01035053289 × 10−526

a9

0.96691

{0.964676, 0.969145}

2.17145789885 × 10−6193

a10

0.063069

{0.0624199, 0.0637180}

2.4388910420 × 10−556

0.999945

a11

−1.966847

{−1.97194278, −1.96175122}

2.8734273447 × 10−292

a12

21.0581

{20.7208, 21.3954}

1.17296332188 × 10−1625

a13

−27.0246

{−28.0223, −26.0269}

2.14835618371 × 10−503

a14

16.23

{15.5168, 16.9432}

4.28626039700 × 10−375

a15

207.783

{203.66, 211.906}

9.1427403949 × 10−1256

a16

−488.161

{−499.149, −477.174}

1.48225067124 × 10−1063

a17

176.29

{169.521, 183.06}

1.40366406588 × 10−471

a18

1.88453

{1.87601, 1.89306}

4.6430138718 × 10−4494

a19

3.05921

{3.03467, 3.08375}

5.5399223318 × 10−3099

As shown in Table 5, within the range of pseudo-reduced temperatures \((1.15 \le T_{pr} \le 3)\) and pseudo-reduced pressures \((0.2 \le P_{pr} \le 15)\), Eq. 14 outperforms Heidaryan et al.’s (2010) correlation in terms of correlation regression coefficient, average percentage error and root mean square of error, with the exception of maximum percentage error. Most importantly, the new correlation is continuous over the entire pseudo-pressure range. Therefore, it would allow for computation of the derivatives of the z-factor over the whole range \((0.2 \le P_{pr} \le 15)\), which is not possible with other explicit correlations.
Table 5

Comparison of the explicit correlations with the experimental data

Models

Maximum absolute error

Coefficient of regression

Maximum percentage error

Average percentage error

Root mean square of percentage error

Sanjari and Lay (2012)

0.7664

0.94946

45.5651

3.7463

7.3258

Heidaryan et al. (2010)

0.0220

0.99963

3.71630

0.4876

0.7369

Azizi et al. (2010)

0.3543

0.87240

60.0251

13.5907

15.7493

Equation 14

0.0270

0.99972

5.9976

0.4379

0.6929

Equation 16

0.0396

0.99899

8.7970

0.8267

1.2430

An application of the new correlation shown in Eq. 17 produces a good correlation of regression of 0.9999 between \(z_{\exp } C\) and \(1 + MP_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right)\). The maximum relative error is the same as that in Eq. 14. This maximum error is shown in Fig. 8 to occur at \(P_{pr} = 2\) and \(T_{pr} = 1.15\).
Fig. 8

Contour plot of relative error

Plots of the z-factors generated using the three most recent explicit correlations (Sanjari and Lay 2012; Heidaryan et al. 2010; Azizi et al. 2010) were compared with those generated using Eqs. 14 and 16 (Fig. 9). While Sanjari and Lay (2012) and Azizi et al. (2010) show marked deviations from the unit line, Heidaryan et al. (2010) and Eqs. 14 and 16 fall on the unit line. This shows that the correlations of Heidaryan et al. (2010) and Eqs. 14 and 16 (and by extension Eq. 17) are better at predicting the values of the z-factor than those of Sanjari and Lay (2012) and Azizi et al. (2010). Since these functions have no point of discontinuity, they can be used in applications where the derivative of the z-factor with respect to its independent variables is required.
Fig. 9

Cross plot comparing several explicit correlations

Example calculations

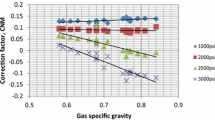
With Figs. 1 and 5, evaluate and compare the compressibility factor of a 0.7 gravity gas at 2000 psig and 150 °F.

From Sutton’s (1985) correlation,
$$T_{pc} = 169.2 + 349.5(0.7) - 74.0(0.7)^{2} = 377.59R$$
$$P_{pc} = 756.8 - 131.07(0.7) - 3.6(0.7)^{2} = 663.29{\text{psig}}$$

Solution 1

$$T_{pr} = \frac{150 + 460}{377.59} = 1.6155, \quad P_{pr} = \frac{2000}{663.29} = 3.0153$$
From Fig. 10, \(z = 0.83\)
Fig. 10

Example illustration 1

Solution 2

$$t = \frac{1}{{T_{pr} }} = 0.619, \quad B = a_{3} t + a_{4} t^{2} + a_{5} t^{6} P_{pr}^{6} = 0.6670$$
$$C = a_{9} + a_{8} tP_{pr} + a_{7} t^{2} P_{pr}^{2} + a_{6} t^{3} P_{pr}^{3} = 1.5829, \quad P_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right) = 6.6713$$
From Fig. 11,
$$zC\left( {T_{pr} = 1.6155, P_{pr}^{2} \left( {1 - \frac{B}{{C^{2} }}} \right) = 6.6713} \right) = 1.32 \to z = \frac{1.32}{1.5829} = 0.8339$$
Fig. 11

Example illustration 2

The problem can also be solved using Eq. 14 directly:
$$z = \frac{{ DP_{pr} (1 + y + y^{2} - y^{3} )}}{{\left( {DP_{pr} + Ey^{2} - Fy^{G} } \right)(1 - y)^{3} }}$$
(18)
$$y = \frac{{ DP_{pr} }}{{\left( {\frac{{1 + A^{2} }}{C} - \frac{{A^{2} B}}{{C^{3} }}} \right)}} ,$$
(19)
where
$$\begin{aligned} & A = a_{1} te^{{a_{2} (1 - t)^{2} }} P_{pr} = 0.62708, \quad D = a_{10} te^{{a_{11} (1 - t)^{2} }} = 0.02934 \\ & E = a_{12} t + a_{13} t^{2} + a_{14} t^{3} = 6.56232,\quad F = a_{15} t + a_{16} t^{2} + a_{17} t^{3} = - 17.08860 \\ & G = a_{18} + a_{19} t = 3.80547, \quad y = \frac{{ DP_{pr} }}{{\left( {\frac{{1 + A^{2} }}{C} - \frac{{A^{2} B}}{{C^{3} }}} \right)}} = 0.10869 \\ \end{aligned}$$
Therefore,
$$z = \frac{{ DP_{pr} \left( {1 + y + y^{2} - y^{3} } \right)}}{{\left( {DP_{pr} + Ey^{2} - Fy^{G} } \right)\left( {1 - y} \right)^{3} }} = 0.8242$$

Conclusions

A simple accurate correlation for evaluating the z-factor that can be linearized has been developed. This correlation performs excellently in the ranges \(1.15 \le T_{pr} \le 3\) and \(0.2 \le P_{pr} \le 15\). It is simple and single-valued. A noteworthy advancement is that the new correlation is continuous over the full range of pseudo-reduced pressures \((0.2 \le P_{pr} \le 15)\). This will widen its applicability to include cases such as the evaluation of natural gas compressibility, in which the derivative of the compressibility factor with respect to the pseudo-reduced pressure is required. For the range outside the coverage of this correlation, implicit correlations can be applied; however, this new explicit correlation can be used to provide an initial guess to speed up the iteration process.

Copyright information

© The Author(s) 2015

Open AccessThis article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.

Authors and Affiliations

  • Lateef A. Kareem
    • 1
  • Tajudeen M. Iwalewa
    • 2
  • Muhammad Al-Marhoun
    • 3
  1. 1.Center for Petroleum and MineralsKing Fahd University of Petroleum and MineralsDhahranSaudi Arabia
  2. 2.Department of Earth SciencesUniversity of CambridgeCambridgeUK
  3. 3.Reservoir Technologies (ResTec)DammamSaudi Arabia

Personalised recommendations