Pseudo-phase equilibrium of light and heavy crude oils for enhanced oil recovery

Abstract

Presented paper, herein, is on phase equilibrium of light and heavy crudes known to be closely related to enhanced oil recovery (EOR). In miscible gas injection, the advancing gas (or injecting fluid) develops with petroleum fluids a miscibility front in the reservoir fluids that further reduces the viscous forces holding crudes stranded. The present work presents a phase equilibrium scheme upon which heavy oil swelling and light crude vaporization were found when carbon dioxide (or methane) was used as advancing gas. Heavy crude swelling was observed to be not only dependent on gas solubility but also on the chemical composition of the crude oil. Although a small fraction of injecting gas was distributed in the reservoir water, the initial water–oil ratio was seen to alter the bubble-point pressure from 10 to 30 % depending of the injected gas. In order to mimic miscible-like behavior during gas injection, a dynamic description of methane and carbon dioxide was proposed. Alteration of PVT parameters below and beyond the bubble-point pressure was highlighted therefrom.

Introduction

It is a well-known fact that a substantial amount of crude oil reserves remains untapped. Around 2 trillion barrels of conventional oil and 5 trillion barrels of heavy oil are estimated worldwide (Abdul-Hamid et al. 2013). From an economic point of view, there is a certain interest in developing recovery techniques that may produce more oil after primary stage (natural oil drive) and second stage, i.e., water flooding (Thomas 2008). Miscible gas flooding, among which, carbon dioxide flooding (CO₂-EOR) is believed to be the second largest recovery means to be applied in an oilfield after thermal EOR (Kokal and Al-Kaabi 2010; Yousefi-Sahzabi et al. 2011). Successfully implemented for light and medium crudes with a considerable amount of oil recovered (Taber et al. 1997), CO₂-EOR has drawn, however, less attention for heavy crudes. The poor acceptable sweeping efficiency and its unlikeliness to develop a miscible front were referred as primary reasons of such deterrence (Cuthiell et al. 2006; Chukwudeme and Hamouda 2009). Moreover, CO₂ miscible injection has to challenge deposition of heavy organic fractions. In other words, heavy hydrocarbon fractions tend to be stripped out of the crude during CO₂ flooding (Zhang et al. 2007; Chukwudeme and Hamouda 2009; Moradi et al. 2012; Jafari et al. 2012; Cao and Gu 2013). Asphaltene is reported to cause well-plugging, pipeline-fouling, as well as desaphalting original crude (Brons and Yu 1995; Wilt et al. 1998). Several cases of asphaltene deposition have been reported. Nevertheless, some fields have attempted to extract untapped heavy crudes using CO₂ as primary advancing gas for tertiary recovery (Tzimas et al. 2005; Parracello et al. 2011).

Fundamentally, CO₂-EOR operates in a simple manner. Given the right conditions, CO₂ mixes with crude oil (or mixture crude + gas) behaving like a thinning agent. The oil viscosity is, thereby, reduced and flushed out from oil reservoir by the means of water (Donaldson et al. 1989). In typical oil reservoir, it is common to find water that coexists with trapped crudes in the form of brine (or connate water). Brine, which consists mainly of sodium chloride (NaCl), has a concentration reported much higher to than of typical seawater. Often, it ranges from 1 to 30 wt% NaCl (Tarek 2007). During gas injection, the gas comes in contact with reservoir fluid(s) distributing immiscible fluids into distinct thermodynamic phases including gas rich, hydrocarbon rich, and water rich. Because of the complex chemical composition of the crude oil, the phase distribution computation is reported laborious. Thus, it is acceptable to model crude oil as a single component. Rather to singularize crude oil as a pseudo-component, this work has computed thermodynamic phase composition using crude oil modeled from its actual chemical composition.

Heidemann (1974) analyzed a pseudo-ternary phase equilibria consisting of methane–butane–water in which butane was used to model light crudes. The phase composition was performed aided with Redlich-Kwong equation of state (RKEOS) (Soave 1972). Phase equilibrium calculations were later improved by Peng and Robinson (1976) who investigated into (butane:1-butene:water)—system. Through a modified equation of RKEOS, they proposed an algorithm that accounted the composition of displacing gas in each different thermodynamic phase. However, extensive iterative calculations as well as the composition of brine were highlighted as major weak points of their work. Li and Nghiem (Li and Nghiem 1986) proposed to combine Peng-Robinson EOS (PREOS) with Henry’s law to compute gas solubility in oil-rich and water-rich phases at different brine solutions. An attempt to mitigate excessive iterations was discussed by (Xu et al. 1992). They developed an accelerated technique, which reduces the computational time for multicomponent phase equilibria. In this regard, over the past decades, several computational schemes proposed to model not only crude oil but also brine composition (Whitson and Michelsen 1989; Mokhatab 2003; Lapene et al. 2010). However, the literature does not report an approach whereby actual crude and/or its chemical composition is used during the modeling of petroleum thermodynamics.

Therefore, the present study presents the pseudo-equilibrium of actual dead crude oils modeled from their chemical composition. A computational scheme, modified from established algorithms, is further proposed. Moreover, this work attempts to highlight in simple manner how does the phase composition of petroleum fluids could be correlated with basic PVT parameters including bubble-point pressure, solution gas–oil ratio (GOR) and oil formation volume factor (Bo).

Experimental procedure and apparatus

Materials

Experimental phase distribution measurements were conducted, in the present work, on two dead crude oil samples. The respective reservoir waters were synthetically prepared. A summary of the physicochemical properties of both crudes and brine solutions is outlined in Table 1.

Table 1 Physical and chemical properties of investigated petroleum fluids

Carbon dioxide (CO₂) and methane (CH₄) were selected as advancing gases. Both were supplied by Itochu Industry gas Ltd (Japan) and had a purity of 99.99 %. The choice of CH₄ targeted to gauge solubility and sweeping efficiency of CO₂ vis-à-vis of a common lean gas. NaCl purchased from Junsei Chemical (Japan), calcium chloride (CaCl₂) and magnesium chloride hexahydrated (MgCl₂·6H₂O) both purchased from Wako Pure Chemical Industries (Japan) were used as raw materials to prepare different brine solutions.

Apparatus and operating conditions

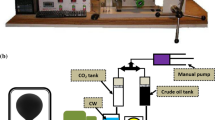
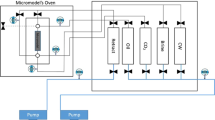
A multi-contact test including gas injection is conducted, at a laboratory scale, through an apparatus known as PVT equipment. A schematic of the analyzing cell of the PVT from which solubility of gas in oil and ratio of phase volume of oil to that of injected gas were computed is depicted in Fig. 1.

Fig. 1

Schematic of PVT analyzing cell as set-up in this work

In general, its principle depends upon the change in system pressure at either a constant temperature or constant volume or both, recorded in function of time. The PVT analyzing cell was assumed to model a homogeneous oil reservoir without rock formation. Operating conditions, close to the actual oilfield from which the samples were collected, were reproduced within the PVT cell to give realistic data. Depending on the investigated hydrocarbon system, the water–oil ratio (WOR), defined as the amount of brine in immiscible state with dead crude oil, was changed. WOR, therefrom considered, was representative of oil reservoir conditions after water flooding.

A summary of petroleum systems studied, the displacing gas state as well as their injecting conditions is outlined in Table 2.

Table 2 Investigated petroleum fluids and experimental conditions

Thermodynamics of petroleum fluids

If an oil reservoir were to be modeled by PVT analyzing cell, a typical isothermal cell pressure–contacting time would be similar to Fig. 2.

Fig. 2

Experimental isothermal pressure–volume profile A gas injection; AB diffusion and solubility of advancing gas in liquid phase; BC equilibrium between thermodynamic phases; CD thermodynamic equilibrium broken by mechanical compression of piston

Upon injection (A on Fig. 2), the displacing gas (CO₂/CH₄) will diffuse and dissolve rapidly in the (crude oil + brine)-rich phase (AB). Miscibility is to be reached within the cell through a phase composition changes subsequent to a multiple contact and mass transfer between analyzing cell fluids, i.e., crude oil, brine, and injected gas. The displacement of oil by gas is highly efficient when the thermodynamic properties of the advancing gas and crude oil become similar. In other words, given a sufficient time, crude oil-rich, water-rich, and gas-rich phases ultimately attain a thermodynamic equilibrium (BC).

For 1 mol of mixture (crude oil + brine), the material balance across the PVT cell for a component i which has an overall mole fraction z _i , a mole fraction x _i in an oil-rich phase l, x _wi in brine-rich w, and y _i in gas-rich phase v is expressed by Eqs. (1) and (2):

$$n^{l} + n^{w} + n^{v} = 1,$$

(1)

$$x_{i} n^{l} + x_{{w_{i} }} n^{w} + y_{i} n^{{_{v} }} = z_{i},$$

(2)

where n ^l, n ^w, and n ^v are the number of moles of oil-rich, brine-rich, and vapor-rich phases, respectively.

Equation (3) describes the relation between the different phases of the cell of n components,

$$\sum\limits_{i = 1}^{n} {x_{i} } = \sum\limits_{i = 1}^{n} {x_{{w_{i} }} } = \sum\limits_{i = 1}^{n} {y_{i} } = \sum\limits_{i = 1}^{n} {z_{i} } = 1.$$

(3)

Let $K_{{a_{i} }}$ and $K_{{w_{i} }}$ to define equilibrium ratio in oil-rich phase and brine-rich phase, respectively. Both were computed from Eqs. (4) and (5), respectively:

$$K_{{a_{i} }} = \frac{{y_{i} }}{{x_{i} }} = \frac{{\phi_{i}^{l} }}{{\phi_{i}^{v} }},$$

(4)

$$K_{{w_{i} }} = \frac{{y_{i} }}{{x_{{w_{i} }} }} = \frac{{\phi_{i}^{w} }}{{\phi_{i}^{v} }},$$

(5)

where $\varPhi_{i}^{l}$, $\varPhi_{i}^{w}$, and $\varPhi_{i}^{v}$ are the fugacity coefficients of i in the crude oil-rich phase, brine-rich phase, and the gas-rich phase, respectively.

The fugacity coefficients in different thermodynamic phases were computed using PREOS as expressed in Eq. (6):

$$\begin{aligned} \ln \phi_{i}^{l,w,v} &= \frac{{b_{i} }}{{b_{m} }}(Z_{i}^{l,w,v} - 1) - \ln (Z_{i}^{l,w,v} - B) \\ &\quad + \frac{A}{{2\sqrt {2B} }}\left( {\frac{2}{{a_{m} }}\sum {y_{i} a_{ij} } - \frac{{b_{i} }}{{b_{m} }}} \right)\times\ln \left( {\frac{{Z_{i}^{l,w,v} \, + \, (\sqrt 2 + 1)B}}{{Z_{i}^{l,w,v} \, - \, (\sqrt 2 - 1)B}}} \right), \end{aligned}$$

(6)

where Z ^l,w,v _i expresses the compressibility factor of component i in a specific thermodynamic phase. Equation (7) was used to compute the compressibility factor:

$$Z^{3} - (1 - B)Z^{2} + (A - 2B - 3B^{2} )Z - (AB - B^{2} - B^{3} ) = 0.$$

(7)

In Eqs. (6) and (7), a _i , b _i , a _m , b _m, A, and B are constants defined by Peng-Robinson (1976).

Based on the experimental conditions, $K_{{a_{i} }}$ was estimated using a modified Wilson’s correlation (Whitson and Torp 1981):

$$K_{{a_{i} }} = \left( {\frac{{p_{{c_{i} }} }}{{p{}_{{k_{i} }}}}} \right)^{A - 1} \left( {\frac{1}{{p_{{r_{i} }} }}} \right)\exp \left[ {5.37A(1 + \omega_{i} )\left( {\frac{1}{{T_{{r_{i} }} }}} \right)} \right],$$

(8)

where $p_{{c_{i} }}$ is the critical pressure of i, in Pa;

$p_{{r_{i} }}$ and $T_{{r_{i} }}$ are its reduced pressure and temperature, respectively, dimensionless;

ω _i is the acentric factor, dimensionless;

A is dimensionless coefficient.

In Eq. (8), a convergence pressure, p _k, was incorporated. It not only mitigates the non-convergence at high pressures but also provides reliable estimation for supercritical components.

This has been performed to propose a response to the  warning  raised by Barrufet et al. (1995) in regard of prediction of equilibrium ratio. They reported  unrealistic results as well as a non-convergence at high pressures (Barrufet et al. 1995; Wu and Chilingar 1997). Additionally, this work did not experiment high pressures as the equilibrium pressures for most of the cases were found below 17 MPa.

The convergence pressure and the coefficient were given by Eqs. (9) and (10), respectively:

$$p_{{k_{i} }} = 0.414{\text{MW}}_{i} - 290,$$

(9)

where MW _i is the molecular weight of the fluid/component i considered, in kg/mol.

$$A = 1 - \left( {\frac{{p_{\text{inj}} - p_{\text{atm}} }}{{p_{{k_{i} }} - p_{\text{atm}} }}} \right)^{0.6}$$

(10)

where p_inj is the injecting pressure, in Pa;

p _atm is atmospheric pressure, p _atm = 0.101325 × 10⁶Pa;

$p_{{k_{i} }}$ is the convergence pressure, in Pa.

$K_{{w_{i} }}$ was computed using a correlation proposed by Peng and Robinson (1976):

$$K_{{w_{i} }} = 10^{6} \left( {\frac{{T_{{r_{i} }} }}{{p_{{r_{i} }} }}} \right),$$

(11)

Combining Eqs. (1)–(5), the phase composition of the PVT analyzing cell at each equilibrium pressure was, therefore, estimated by Eqs. (12)–(14):

$$\sum\limits_{i = 1}^{n} {x_{i} } \frac{{z_{i} }}{{n^{{_{l} }} (1 - K_{{a_{i} }} ) + n^{w} \left( {\frac{{K_{{a_{i} }} }}{{K_{{w_{i} }} }} - K_{{a_{i} }} } \right) + K_{{a_{i} }} }},$$

(12)

$$\sum\limits_{i = 1}^{n} {x_{{w_{i} }} } = \frac{{z_{i} \left( {{\raise0.7ex\hbox{${K_{{a_{i} }} }$} \!\mathord{\left/ {\vphantom {{K_{{a_{i} }} } {K_{{w_{i} }} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${K_{{w_{i} }} }$}}} \right)}}{{n^{{_{l} }} (1 - K_{{a_{i} }} ) + n^{w} \left( {\frac{{K_{{a_{i} }} }}{{K_{{w_{i} }} }} - K_{{a_{i} }} } \right) + K_{{a_{i} }} }},$$

(13)

$$\sum\limits_{i = 1}^{n} {y_{i} } = \frac{{z_{i} K_{{a_{i} }} }}{{n^{{_{l} }} (1 - K_{{a_{i} }} ) + n^{w} \left( {\frac{{K_{{a_{i} }} }}{{K_{{w_{i} }} }} - K_{{a_{i} }} } \right) + K_{{a_{i} }} }}.$$

(14)

Rather to solve objective functions proposed by (Peng and Robinson 1976; Mokhatab 2003), this study has considered the use of a generalized polynomial form suggested by Weigle (1992). This technique is believed to eliminate two unknowns, i.e., n ^l and n ^w, remaining in Eqs. (12)–(14). Also, Weigle (1992) demonstrated that extensive iterative calculations, required to reach pseudo-equilibrium, were significantly reduced.

Thus, let the dimensionless factor, α, to define the vapor fraction,

$$\alpha = \frac{n}{{n^{v} }}.$$

(15)

Introducing Eq. 15 into Eqs. 12–14, the phase composition was reformulated as expressed by Eqs. 16–18:

$$\sum\limits_{i = 1}^{n} {x_{i} } = \frac{{z_{i} }}{{1 + \alpha (K_{{a_{i} }} - 1)}},$$

(16)

$$\sum\limits_{i = 1}^{n} {x_{{w_{i} }} } = \frac{{z_{i} \left( {{\raise0.7ex\hbox{${K_{{a_{i} }} }$} \!\mathord{\left/ {\vphantom {{K_{{a_{i} }} } {K_{{w_{i} }} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${K_{{w_{i} }} }$}}} \right)}}{{1 + \alpha (K_{{a_{i} }} - 1)}},$$

(17)

$$\sum\limits_{i = 1}^{n} {y_{i} } \frac{{z_{i} K_{{a_{i} }} }}{{1 + \alpha (K_{{a_{i} }} - 1)}}.$$

(18)

By substituting Eqs. (16) in (3) and solving it for $\sum\limits_{i = 1}^{n} {x_{i} - 1 = 0}$, a Rachford-Rice objective function (Eq. 19) is obtained (Rachford and Rice 1952),

$$\sum\limits_{i = 1}^{n} {\frac{{z_{i} (K_{{a_{i} }} - 1)}}{{1 + \alpha (K_{{a_{i} }} - 1)}}} = 0$$

(19)

Since both the overall cell composition and the operating conditions were known, it was then possible to calculate α for both binary and ternary phases by solving Eq. (19).

Hence, for a binary system (n = 2),

$$\alpha = - \left[ {\frac{{z_{1} }}{{(K_{{a_{2} }} - 1)}} + \frac{{z_{2} }}{{(K_{{a_{1} }} - 1)}}} \right].$$

(20)

For a ternary system (n = 3),

$$\alpha^{2} + \alpha \left[ {\frac{{\sum\limits_{i = 1}^{3} {z_{i} \left( {\sum\limits_{j \ne i}^{3} {(K_{{a_{i} }} - 1)} } \right)} }}{{\prod\limits_{j \ne i}^{3} {(K_{{a_{i} }} - 1)} }}} \right] + \sum\limits_{i = 1}^{3} {\frac{{z_{i} }}{{\prod\limits_{j \ne i}^{3} {(K_{{a_{i} }} - 1)} }}} = 0,$$

(21)

α was therefrom used to estimate the phase composition of each phase. Figure 3 summarizes the sequential algorithm, followed in the present study, for both pseudo-binary and pseudo-ternary phase flash calculations.

Fig. 3

Flow diagram of pseudo-binary and ternary compositions mechanical compression of piston

Results and discussions

Phase composition and advancing gas solubility

Phase composition

In a typical miscible CO₂-EOR process, the interest is to account the amount (mole fraction) of gas that dissolves in the oil-rich phase. Tables 3 and 4 outline the mole fraction of CO₂ and CH₄ in binary and ternary systems, respectively.

Table 3 Experimental results of methane and carbon dioxide solubility in dead light and heavy crudes at pseudo-equilibrium pressures

Table 4 Methane and carbon dioxide solubility in (dead crude + brine) medium at saturation pressures

In pseudo-binary medium, as seen in Fig. 4, the mole fraction of CO₂ was found much higher to that of methane. This was expected as the crude oil mainly consists of hydrocarbon chains, i.e., C–H bonds. Likewise is methane (primary hydrocarbon). This similarity in chemical architecture reduces the polarity, thus the solubility (Silverstein 1993). The more hydrocarbons in the crude, i.e., the heavier, the lower is the polarity. That explains why methane is dissolved more in light crude. The presence of oxygen atom, on the other hands, increases the polarity of CO₂ towards free mixing with crude oil. Although a similar pattern was observed with literature, standard deviation showed the influence of chemical composition of the crude in phase equilibrium calculations. In fact, the solubility analysis for selected data was performed on pure components, thus pure critical parameters. This work, however, has modeled crude oils from the compositional analysis of the crude which showed the percentage of each hydrocarbon.

Fig. 4

Mole fraction of CH₄/CO₂ in crude oil-rich phase (open circle) CH₄:SK-1H; (open square) CH₄: SK-3H; (open diamond) CO₂:SK-3H; (filled circle) xCO₂:(1 − x)n − C₁₆/T = 315 K (Tanaka et al. 1993); (filled triangle) xCH₄:(1 − x)n − C₁₀/T = 344 K (Srivastan et al. 1992)

Likewise, when reservoir water is accounted (Fig. 5), mole fraction of gas dissolved was found to decrease significantly compared to if it was not accounted. This observation could be contradicted with results from brine-rich phase solubility (Fig. 6). An order of 10⁻² and 10⁻³ were found for carbon dioxide and methane distribution in the brine, respectively. This suggests that brine-rich phase could possibly be neglected during phase composition computation, especially for methane. Also, an obvious reason could be imputed to the number of phases with which the gas is in contact. This paper, however, believes that reservoir water somewhat develops a kinetic barrier towards free mixing of advancing gas and petroleum fluids. Additionally, it should be bear in mind that, despite the low concentration of gas in water, the reservoir environment may favor chemistry between the reservoir rock formation, brine, and carbon dioxide. Chemistry that invariably leads to scale formation (Kaszuba et al. 2003; Nguele et al. 2014).

Fig. 5

Mole fraction of CH₄/CO₂ in (crude oil + brine)-rich phase (open circle) CH₄: SK-3H:W₂; (open square) CO₂:SK-3H:W₁; (open diamond) CO₂:SK-1H:W₃; (filled square) CO₂:Heavy oil (API 12.4^o)/T = 298.15 K (Bennion and Thomas 1993); (filled circle) CO₂:Bitumen (Cut 1) (Huang and Radosz 1990)

Fig. 6

Mole fraction of CH₄/CO₂ in brine-rich phase (open square) CH₄: SK-3H:W₂; (open circle) CO₂:SK-3H:W₁; (open diamond) CO₂:SK-1H:W₃; (filled square) CO₂:H₂O/T = 318.23 K (Valtz et al. 2004)

Advancing gas solubility in dead crude oils

The solubility of an advancing gas should be viewed as an equilibrium of intermolecular forces between injected gas, in occurrence carbon dioxide or methane, with petroleum fluid (crude oil and/or brine). From afore-computed mole fraction, the injected gas solubility (R _s) was computed from Eq. (22):

$$R_{s,i} = \frac{{{\raise0.7ex\hbox{${x_{i} }$} \!\mathord{\left/ {\vphantom {{x_{i} } {(1 - x_{i} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${(1 - x_{i} )}$}}}}{{W_{\text{FIP}} }}n_{\text{oil,in}},$$

(22)

where x _i defines the mole fraction of component i in the (crude oil + brine)-rich phase, dimensionless.

n _oil,in is the initial number of moles of crude oil, in mol;

W _FIP is the total weight of petroleum fluids-in-place (FIP), i.e., initial crude oil and brine, in kg.

Figures 7 and 8 show the results of the solubility of carbon dioxide and methane in investigated systems, respectively. Both plots highlighted the dependence of the solubility towards the nature of the crude, the injection conditions and to an extent the salinity within the cell. For the same type of crude oil, carbon dioxide dissolved preferentially at a higher rate and larger amount compared to methane. Reasoning discussed before may be applied in here. Similar results were obtained by Bennion and Thomas (1993). This confirmed a multi-contact process occurring within the reservoir (herein modeled by PVT analyzing cell) that distributes thermodynamic phase.

Fig. 7

CO₂ solubility in different petroleum fluids (open circle) CO₂:SK-3H; (open square) CO₂:SK-3H:W₁; (open diamond) CO₂:SK-1H:W₃; (filled square) CO₂:acetone:water/T = 313.75 K (Jödecke et al. 2007)

Fig. 8

CH₄ solubility in different petroleum fluids (open circle) CH₄:SK-1H; (open square) CH₄:SK-3H; (open diamond) CH₄:SK-3H:W₂; (filled square) xCH₄:(1 − x) n − C₁₀/T = 344 K (Srivastan et al. 1992)

In either methane or carbon dioxide injection, the rise seemly followed a linear regression with a curvature above which it increased drastically. The curvature was taken as bubble-point pressure (p _b). The curvature (or in some case the apparent flattening) may be attributed to a pseudo-liquid–liquid equilibrium between the heavy and light fractions of the crude.

It has been shown, so far that, the injection of gas alters thermodynamic properties of the reservoir fluids by changing their chemical compositions. Actual thermodynamic would require identification of all components within the crude in order to have an ideal composition, which is not in reality practical. Thus, crude oil, carbon dioxide/methane and brine were taken as pseudo-components. Figure 9 depicts the pseudo-ternary phase diagram for methane and carbon dioxide in (crude oil + brine) medium.

Fig. 9

Pseudo-ternary diagram representation of CH₄/CO₂ in heavy and light crude in presence of brine (1φ) single-phase region, i.e., total miscibility; (2φ) two-phase region

Therefrom, it could be seen that in the 2-phase region (2φ) as the amount of injected gas built-up, crude oil separated into two phases either vapor–vapor, vapor–liquid, and/or liquid–liquid. 2φ region was observed broader for light crude oils. This implied, that during gas injection, the process by which lighter fractions were vaporized was more pronounced in lighter crude. On the other hand, Fig. 9 revealed a likelihood of heavier components deposition which may lead to asphalt/wax settling if the crude oil candidate was asphaltenic base. To aforestated points, it could be added the naphthenic nature of the crude oils as plausible answer. Figure 9 shows a great importance in reservoir engineering as it gives a compositional gradient of pseudo-components present during gas injection (Dalmolin et al. 2006).

Estimating heavy oil swelling through phase equilibrium

When contacting a reservoir fluid with a solvent (gas), it is known the petroleum fluid will expand. This phenomenon is call oil swelling. The extent to which the swelling will alter oil properties are dependent of reservoir environment and crude properties (Yang et al. 2014). In this work, the crude oil (as expected) was seen to swollen significantly after gas injection. A sample pictogram of swollen crude is illustrated in Fig. 10.

Fig. 10

a Foamy oil collected after carbon dioxide injection; b microscopic visualization. Dark spot encircles represent swollen oil droplets and white spots air bubbles

Let S _f to define the swelling factor, this work has computed oil swelling from Eq. (23):

$$S_{\text{f}} = \left( {\frac{{V_{\text{foam}} }}{{V_{\text{oil,in}} }} - 1} \right),$$

(23)

where S _f, in  %;

V _foam is the volume of foamy oil, in m³;

V _oil,in is the volume of crude oil prior gas injection, in m³.

The swelling was assumed to be strictly due to gas dissolution in the crude oil. In other words, the volume of the foamy oil was taken equal to mole fraction afore-computed of the gas (eventually converted into volume).

As shown in Fig. 11, swelling was found to increase with gas solubility, thus the pressure. A contact of crude oil with methane/carbon dioxide rises up oil saturation which subsequently increases oil relative permeability. This highlights the significance of oil swelling for oil recovery as residual oil saturation determines ultimate recovery (Pedersen and Christensen 2007). Following P-x results (Figs. 4, 5, 6), oil swelling was observed higher for carbon dioxide than methane. Considering aforesaid points, it could be asserted that oil swelling, higher for carbon dioxide injection, will invariably give a better recovery factor for heavy crudes than methane.

Fig. 11

Heavy oil swelling computed from phase composition (open circle) CH₄:SK-3H; (open square) CO₂:SK-3H; (open diamond) CO₂:SK-3H:W₁

Moreover, heavy oil swelling increased following a polynomial linear regression. It, seemly, has a form of y(x) = ax + b where a could be termed as proportional coefficient of gas solubility (dimensionless) and b the correction factor (in units of gas solubility). Table 5 summarizes the experimental values of a and b for considered petroleum fluids.

Table 5 Experimental values of a and b for heavy oil swelling

Proportional coefficient of solubility is strictly dependent on injected gas. The more soluble is the gas, the higher is a. Also, with the presence of reservoir water, oil swelling was increased 3 times. This might be illusionary as only a small fraction of gas is distributed in the brine phase. Thus, the jump in a value is likely to be attributed to the expansion of the petroleum fluid (which is obviously higher with water). The non-uniformity in correction factors could be justified with how the miscibility front is developed. In binary systems, the advancing gas is in contact with a pseudo-single phase while in ternary (or multiple component) system, the sweeping fluid contacts multiple layers. In the latter case, miscible conditions are developed in situ (within the cell) through composition alteration of the injected gas. The interfacial tension (IFT) or surface tension is altered. This leaves the thought that oil swelling is viscosity and IFT dependent (Or et al. 2014).

It should be noted that a care should be exercised if afore-presented coefficients were to be used. The models were performed on dead crudes oil. An interesting approach would be to extend these postulates to live crude oils and to account the deviation.

PVT cell-to-recovery volume relations

In this section, this research proposes to correlate phase composition afore discussed with PVT parameters including bubble-point pressure (p _b), solution gas/oil ratio (GOR), and the oil formation volume factor (B _o) conventionally obtained through flash separation tests (Freyss et al. 1978).

Theoretical prediction of bubble-point pressure from proposed algorithm

Although bubble-point pressure¹ refers to a fluid property, it is, however, important factor from an EOR point of view as it is not recommend to produce oil below p _b (Danesh 1998). Using the algorithm (Fig. 3), it was able to generate equilibrium ratios at each thermodynamic pseudo-equilibrium (Fig. 12). Hence, p _b was predicted by solving Eq. (24):

Fig. 12

Predictive determination of bubble-point pressure of different petroleum fluids systems (open circle) CH₄:SK-1H; (open square) CH₄:SK-3H; (open diamond) CH₄:SK-3H:W₂; (filled circle) CO₂:SK-3H; (filled square) CO₂:SK-3H:W₁; (filled triangle) CO₂:SK-1H:W₃ (1) saturated crude oil; (2) undersaturated crude oil; solid line bubble-point pressure line

$$\sum\limits_{i = 1}^{n} {z_{i} K_{{a_{i} }} } = 1.$$

(24)

Table 6 shows a comparison between the data obtained through this scheme and those from literature. It reveals the dependence of the bubble-point pressure with not only nature of oleic phase but also with experimental results. Also, the reservoir water, according to experimental data, was found to decrease p _b by an order of 11 % for methane and 30 % for CO₂. This observation could be a result of change in WOR which subsequently alter the bubble point.

Table 6 Theoretical and experimental bubble-point pressures of investigated petroleum fluids

Solution gas/oil ratio and oil formation volume factor from phase composition

Petroleum fluids analysis is designed to model the flow of untapped crude oil and the gas contained or injected within. Solution gas/oil ratio (GOR) and oil formation volume factor (Bo) are key parameters in reservoir engineering. The first was referred in this work as the amount of gas, i.e., methane/carbon dioxide dissolved in the crude oil at any given pressure and the latter was modified from its original definition. This paper has associated Bo as the ratio of the volume of (crude oil + brine) prior gas injection to that of the (crude oil + dissolved gas). To an extent, this definition expresses the oil saturation (thus its relative permeability).

Equations (25) and (26) are the mathematical relations of aforementioned definitions, respectively:

$$GOR = \frac{{n^{l} MW_{\text{app}}^{l} \rho_{\text{oil}} }}{{W_{\text{oil}} \rho_{\text{app}}^{l} }},$$

(25)

$$Bo = \frac{{V_{\text{oil}} }}{{V_{\text{FIP}} }},$$

(26)

where GOR is the solution gas/oil ratio, in m³ CO₂(CH₄)/m³ (crude + brine);

Bo is the oil volume factor, in m³ oil/m³ (crude + brine);

n ^l is the number of moles of oil in oil-rich phase, in mol;

MW ^l_app is the apparent molecular weight of the oil-rich phase, kg/mol;

ρ ^l_app is the apparent hydrocarbon-rich phase, in kg/m³;

W _oil is the mass of candidate dead crude oil in kg;

V _oil is the volume of candidate dead crude oil, in m³;

ρ _oil is the density of candidate dead crude oil, in kg/m³;

V _FIP is the volume of (crude + brine), in m³.

The terminology FIP, Fluid-in-place, was used by extension to represent initial crude oil–water in the cell.

Depending on the state of the crude oil² (or crude oil + brine) within the PVT analyzing cell, GOR and Bo behaved differently. At an undersaturated crude oil (Fig. 13), a decrease for both parameters with pressure was observed. The loss in petroleum fluids volume with evolution of injected gas and the decrease in displacing gas pressure are plausible answers. Furthermore, GOR and Bo results concord with predictive bubble-point pressure analysis (Fig. 12) at which this system was determined below the bubble-point line.

Fig. 13

GOR and Bo for a undersaturated crude oil (filled circle) GOR; (open circle) Bo

For saturated systems (Fig. 14), on the other hand, below the bubble point, an increase with the pressure until the bubble-point pressure was reached. This is credited to fluid expansion which simultaneously causes the dead oil to swell (in the case of dead heavy oil) or to vaporize (in case of dead light crude). Either effect explains, also, the sudden peak observed beyond the bubble-point pressure. Similar behaviors were reported by Bennion and Thomas (1993) and more recently by Zirrahi et al. (2014) who investigated in heavy oils and bitumen respectively. Beyond the bubble-point pressure, the concentration of gas is reduced because of its solubility (or relative solubility in case of methane injection). Consequently, the GOR will tend to be constant.

Fig. 14

GOR and Bo for saturated systems (filled circle GOR, open circle Bo) CO₂:SK-3H; (filled triangle GOR, open diamond Bo) CH₄:SK-3H:W₂

Comparative description of dynamic CO₂/CH₄ injection for heavy crude oils

In a multiple contact experiment, into which this work could be categorized, the advancing gas (CO₂/CH₄) and petroleum fluids are not expected to mix immediately upon injection. However, a chemical exchange has to occur to achieve the desired miscibility (Terry 2001).

That is to say that the more injection fluid is reactive (less polar), the higher is the likelihood of the gas to achieve a miscibility. Figure 15 illustrates a dynamic representation that describes the process of gas injection at the experimental level for methane and carbon dioxide. Also, it correlates the phase composition with the parameters.

Fig. 15

Dynamic miscibility description of heavy crude by gas injection a supercritical methane injected; b subcritical carbon dioxide

Gas solubility along with heavy oil solubilization increases with the pressure across these zones. Given the same conditions, methane will dissolve less in heavy crude not only because of its poor reactivity but also due to its high minimum miscibility pressure (Kulkarni and Rao 2005). One way to increase methane solubility would be to get it enriched with a fraction of C₂–C₄ (Teletzke et al. 2005). In addition, oil swelling, whose significance has been discussed in earlier sections, would be higher for carbon dioxide than methane. Although the effect of reservoir water in the phase behavior could be neglected, primarily because of low distribution of gas, it is, however, believed to alter the bubble-point pressure.

Conclusions

In this paper, phase equilibrium of dead crude oils and reservoir water contacted by methane or carbon dioxide was investigated. A computational scheme, modified from known algorithms, was proposed. Therefrom, the phase composition of gas, crude oil and brine-rich phases were computed and correlated with PVT parameters. Major findings of this work are highlighted below:

• 1. Carbon dioxide and methane solubility showed a strong dependence on PVT analyzing cell environment, the nature of crude oil and less to the water salinity composition.

• 2. Heavy oil swelling, prompted by gas solubility, was found to agree with literature and linearized relationship between both parameters was proposed. However, crude oil expansion, due to loss of gas in its vapor phase, altered the oil swelling.

• 3. The algorithm showed an average deviation of 4 % for carbon dioxide injection and 8 % for methane for predictive bubble-point pressure with the literature. This pointed out the dependence of phase composition thus PVT parameters with the composition of crude.

• 4. Lastly, the presence of reservoir water, regardless of its chemical composition, was found to lessen bubble-point pressure.