Introduction

Tight gas reservoirs have features of tiny pores, narrow throats and extremely low permeability. Wells produce at a low natural productivity so that most of wells need the stimulation treatment of fracturing. Recently, the performance of fractured vertical well has been widely studied by many researchers. With conformal transformation, Wang et al. (2003) and Jiang (2001) derived the deliverability equation of fractured vertical well and studied the corresponding pressure performance. Li et al. (2008) established the trinomial deliverability equation of fractured vertical gas well in ultra-low-permeability reservoirs by linear regression with bottom-hole pressure and gas production. Yang et al. (2003) proposed a model by considering the gas flow in reservoirs after fracturing as a combination of radial flow and linear flow and obtained the deliverability equation by integral calculation. In their study, the effects of fracture length, effective permeability and effective thickness on the production after fracturing were investigated. Yin et al. (2005) built up a mathematic model of bilinear flow for fractured vertical well and presented the solution. They also plotted and analyzed the theoretical IPR curves of fractured vertical well. Using elliptic flow model, Li et al. (2005) derived the deliverability equation of fractured vertical well with the consideration of threshold pressure gradient. Based on the theory of steady-state flow, Xiong et al. (2012) used the concept of pseudo-pressure to obtain the deliverability equation for predicting the performance of fractured vertical well in low-permeability gas reservoirs. The equation in their study featured the assumptions of finite conductivity fracture and the consideration of threshold pressure, slippage effect and stress sensitivity. Based on the characteristics and flow law of ellipse system, Luo et al. (2005) proceeded from the generalized Darcy law and synthesized the flow inside and outside the fracture to derive the deliverability equation in steady state for gas reservoirs and obtain the corresponding open flow capacity of fractured vertical gas well. According to the concept of disturbance ellipse and the idea of equivalent rectangle system, Zhou et al. (2009) gained the productivity predictions for the gas well after fracturing in low-permeability reservoirs and plotted the corresponding IPR curves for analysis. Study on productivity of fractured vertical well in above documents all contain the assumptions that boundary conditions are constant pressure and the flow is in steady state, which cannot be appropriate for the pseudo-steady state in reservoirs.

During the depletion in oil or gas reservoirs, flow in pseudo-steady state begins when the pressure wave reaches the closed boundary with the feature that the decrements of pressure at points from borehole walls to boundary gradually tend to be the same. Thus, it is significant for the development of tight gas to investigate the characteristics of IPR curve in this pseudo-steady state. Lian et al. (2013) derived a deliverability equation in pseudo-steady state for oil reservoirs with closed outer boundary. They considered the effects of stress sensitivity and degasification in bottom, and also investigated the stress-sensitive effect on production. Li et al. (2009) took the characteristics of non-linear flow into account to derive the deliverability equation in pseudo-steady state for gas well. Liao (1998) investigated the characteristics of pressure response in pseudo-steady state of deviated wells by considering the oil reservoirs as dual porous media. In this paper, a percolation model of pseudo-steady flow with the consideration of stress-sensitive effect was proposed to derive a deliverability equation of fractured vertical gas well featuring the non-linear flow of gas. The analysis we made on the effects of stress-sensitive coefficient, matrix permeability, fracture length and fracture conductivity on the productivity of fractured vertical gas well is significant for the tight gas development.

Model establishment

Assumptions

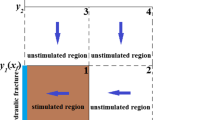
Fracturing for vertical gas well induces the decrease of percolation resistance and variation of flow pattern in which the gas flow is pseudo-radial inside the fracture and linear outside the fracture (Abbaszadeh and Hegeman 1990). Assumptions specifically include the following: (1) formation thickness is equal, outer boundary is closed, production rate is constant and percolation reached the pseudo-steady state. (2) Vertical fracture is symmetrical about the borehole and vertically penetrating the formation. (3) Flow inside the fracture is one-way turbulent and gas flowing to borehole is only along the fracture. (4) Flow outside the fracture is pseudo-radial; isobars are elliptical and perpendicularly crossed by streamlines. (5) The damage to fracture surface is not considered.

Flow outside the fracture

During the production of fractured vertical well, elliptical percolation in 2D plane is induced, namely that elliptical isobars and corresponding conjugate hyperbolic streamlines form by focusing on end points of fracture. The relation between Cartesian coordinates and elliptic coordinates can be written as

$$x = x_{\text{f}} {\text{ch}}\xi \cos \eta ;y = x_{\text{f}} {\text{sh}}\xi \sin \eta .$$
(1)

By Eq. (1), equations of elliptical isobars and hyperbolic streamlines can be obtained and written as below

$$\left\{ \begin{aligned} &\frac{{x^{2} }}{{\left( {x_{\text{f}} {\text{ch}}\xi } \right)^{2} }} + \frac{{y^{2} }}{{\left( {x_{\text{f}} {\text{sh}}\xi } \right)^{2} }} = 1 \hfill \\ &\frac{{x^{2} }}{{\left( {x_{\text{f}} \cos \eta } \right)^{2} }} - \frac{{y^{2} }}{{\left( {x_{\text{f}} \sin \eta } \right)^{2} }} = 1 \hfill \\ \end{aligned} \right..$$
(2)

Based on the concept of disturbance ellipse, elliptical isobars can be described by equivalent rectangle patterns as follows.

$$\bar{x} = x_{\text{f}} {\text{ch}}\xi ;\quad \bar{y} = \frac{2}{\pi }\int_{0}^{{{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {x_{\text{f}} {\text{sh}}\xi \sin \eta } {\text{d}}\eta = \frac{{2x_{\text{f}} }}{\pi }{\text{sh}}\xi$$
(3)

In consideration of the stress-sensitive effect and the non-linear flow in tight gas, the equation of the flow to fracture is written as

$$\frac{{{\text{d}}p}}{{{\text{d}}y}} = \frac{\mu }{{k_{0} e^{{\alpha \left( {p - p_{0} } \right)}} }}v + \beta \rho v^{2} .$$
(4)

According to the definition of gas isothermal compressibility, the total elastic volume in control area of a certain gas well is as follows

$$V\left( t \right) = c_{\text{g}} V_{t} \left( {p_{ 0} - \bar{p}\left( t \right)} \right)$$
(5)

where

$$V\left( t \right) \approx \pi \left( {x_{\text{f}}^{2} {\text{sh}}\xi_{\text{e}} {\text{ch}}\xi_{\text{e}} - x_{\text{f}} w_{\text{f}} } \right)h$$
$$\xi_{\text{e}} = \ln \left[ {{{r_{\text{e}} } \mathord{\left/ {\vphantom {{r_{\text{e}} } {x_{\text{f}} }}} \right. \kern-0pt} {x_{\text{f}} }} + \sqrt {\left( {{{r_{\text{e}} } \mathord{\left/ {\vphantom {{r_{\text{e}} } {x_{\text{f}} }}} \right. \kern-0pt} {x_{\text{f}} }}} \right)^{2} - 1} } \right].$$

And the gas production can be expressed as

$$q_{\text{sc}} \left( t \right)B_{\text{g}} = \frac{{{\text{d}}V\left( t \right)}}{{{\text{d}}t}} = - c_{\text{g}} V_{\text{t}} \frac{{{\text{d}}\bar{p}\left( t \right)}}{{{\text{d}}t}} = - c_{\text{g}} \pi \left( {\frac{{x_{\text{f}}^{2} {\text{sh}}\left( {2\xi_{\text{e}} } \right)}}{2} - x_{\text{f}} w_{\text{f}} } \right)h\frac{{{\text{d}}\bar{p}\left( t \right)}}{{{\text{d}}t}}.$$
(6)

Rate of flow through any isopiestic pressure section in the well controlling area is expressed as

$$q_{\text{sc}} \left( {\xi ,t} \right)B_{\text{g}} = - c_{\text{g}} \pi \left( {\frac{{x_{\text{f}}^{2} {\text{sh}}\left( {2\xi_{\text{e}} } \right) - x_{\text{f}}^{2} {\text{sh}}\left( {2\xi } \right)}}{2}} \right)h\frac{{{\text{d}}\bar{p}\left( t \right)}}{{{\text{d}}t}}.$$
(7)

Due to x fsh(2ξ e) ≫ 2w f, it can obtain Eq. (8) as

$$q_{\text{sc}} \left( {\xi ,t} \right) = \frac{{x_{\text{f}}^{2} {\text{sh}}\left( {2\xi_{\text{e}} } \right) - x_{\text{f}}^{2} {\text{sh}}\left( {2\xi } \right)}}{{x_{\text{f}}^{2} {\text{sh}}\left( {2\xi_{\text{e}} } \right) - 2x_{\text{f}} w_{\text{f}} }}q_{\text{sc}} \left( t \right) \approx \left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)q_{\text{sc}} \left( t \right).$$
(8)

Transform q sc(ξ, t) to q g in subsurface conditions

$$q_{\text{g}} = \frac{{p_{\text{sc}} zT}}{{T_{\text{sc}} p}}\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)q_{\text{sc}} \left( t \right).$$
(9)

For an isopiestic ellipse with a semi-major axis of x fchξ and a semi-minor axis of x fshξ, the flow velocity can be written as

$$v = \frac{{q_{\text{g}} }}{l\left( \xi \right)h}$$
(10)

where

$$l\left( \xi \right) = 4x_{\text{f}} {\text{ch}}\xi \int_{0}^{\pi } {\sqrt {1 - \left( {1 - th^{2} \xi } \right)\sin^{2} t} } {\text{d}}t.$$

With the chain rule, we can obtain

$$\frac{{{\text{d}}p}}{{{\text{d}}y}} = \frac{{{\text{d}}p}}{{{\text{d}}\bar{y}}} = \frac{{{\text{d}}p}}{{{\text{d}}\xi }}\frac{d\xi }{{d\bar{y}}} = \frac{\pi }{{2x_{\text{f}} {\text{ch}}\xi }}\frac{{{\text{d}}p}}{{{\text{d}}\xi }}.$$
(11)

Introduce the variable of pseudo-pressure \(U\left( p \right) = \int_{{p_{0} }}^{p} {\frac{{pe^{{\alpha \left( {p - p_{0} } \right)}} }}{\mu z}{\text{d}}p}\), and substitute Eqs. (9), (10) and (11) into Eq. (4), we can obtain

$${\text{d}}U = \frac{{4x_{\text{f}} p_{\text{sc}} T}}{{\pi T_{\text{sc}} }}\left( \begin{aligned} &\frac{{q_{\text{sc}} }}{{k_{0} h}}\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)\frac{{{\text{ch}}\xi }}{l\left( \xi \right)} \hfill \\ &+ \frac{{\beta \rho_{\text{sc}} q_{\text{sc}}^{2} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{\bar{\mu }h^{2} l^{2} \left( \xi \right)}}\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)^{2} {\text{ch}}\xi \hfill \\ \end{aligned} \right){\text{d}}\xi .$$
(12)

With the boundary conditions, in the boundary of well controlling area, there is

$$U_{\text{e}} = \left. U \right|_{{r = r_{\text{e}} }} = \int_{{p_{0} }}^{{p_{\text{e}} }} {\frac{{pe^{{\alpha \left( {p - p_{0} } \right)}} }}{\mu z}{\text{d}}p} .$$
(13)

Solving Eq. (13), the pressure in an isopiestic ellipse with semi-major axis of x fchξ and semi-minor axis of x fshξ can be obtained

$$U\left( \xi \right) = U_{\text{e}} - \frac{{4x_{\text{f}} p_{\text{sc}} T}}{{\pi T_{\text{sc}} }}\left( \begin{aligned} &\frac{{q_{\text{sc}} }}{{k_{0} h}}\int_{\xi }^{{\xi_{\text{e}} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)\frac{{{\text{ch}}\xi }}{l\left( \xi \right)}{\text{d}}\xi } \hfill \\ &+ \frac{{\beta \rho_{\text{sc}} q_{\text{sc}}^{2} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{\bar{\mu }h^{2} }}\int_{\xi }^{{\xi_{\text{e}} }} {\frac{{{\text{ch}}\xi }}{{l^{2} \left( \xi \right)}}\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)^{2} {\text{d}}\xi } \hfill \\ \end{aligned} \right).$$
(14)

The average pseudo-pressure in gas supply area is

$$\bar{U} = \frac{{\int_{0}^{{\xi_{\text{e}} }} {\left( {{\text{sh}}^{2} \xi + {\text{ch}}^{2} \xi } \right)U\left( \xi \right){\text{d}}\xi } }}{{{\text{sh}}\left( {\xi_{\text{e}} } \right){\text{ch}}\left( {\xi_{\text{e}} } \right)}}.$$
(15)

Substitute Eq. (15) into Eq. (14) to obtain Eq. (16)

$$\bar{U} = U_{\text{e}} - \frac{{8x_{\text{f}} p_{\text{sc}} T}}{{\pi T_{\text{sc}} {\text{sh}}2\xi_{\text{e}} }}\int_{0}^{{\xi_{\text{e}} }} {\left( \begin{aligned} \frac{{q_{\text{sc}} \left( {{\text{sh}}^{2} \xi + {\text{ch}}^{2} \xi } \right)}}{{k_{0} h}}\int_{\xi }^{{\xi_{\text{e}} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi^{\prime } } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)\frac{{{\text{ch}}\xi^{\prime } }}{{l\left( {\xi^{\prime } } \right)}}{\text{d}}\xi^{\prime } + } \hfill \\ \frac{{\beta \rho_{\text{sc}} q_{\text{sc}}^{2} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{\left( {\frac{{\bar{\mu }h^{2} }}{{\left( {{\text{sh}}^{2} \xi + {\text{ch}}^{2} \xi } \right)}}} \right)}}\int_{\xi }^{{\xi_{e} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi^{\prime } } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)^{2} \frac{{{\text{ch}}\xi^{\prime } }}{{l^{2} \left( {\xi^{\prime } } \right)}}{\text{d}}\xi^{\prime } } \hfill \\ \end{aligned} \right){\text{d}}\xi } .$$
(16)

With Eq. (16), we can obtain the pseudo-pressure U w1 in ξ = 0. And combine U w1 and Eq. (16), we can obtain the follow equation

$$\bar{U} - U_{\text{w1}} = Aq_{\text{sc}} + Bq_{\text{sc}}^{2}$$
(17)

where

$$\begin{aligned} A = & \frac{{4x_{\text{f}} p_{\text{sc}} T}}{{\pi k_{0} hT_{\text{sc}} }}\int_{0}^{{\xi_{e} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)\frac{{{\text{ch}}\xi }}{l\left( \xi \right)}{\text{d}}\xi } \\ - \frac{{8x_{\text{f}} p_{\text{sc}} T}}{{\pi k_{0} hT_{\text{sc}} {\text{sh}}\left( {2\xi_{\text{e}} } \right)}}\int_{0}^{{\xi_{e} }} {\left( {{\text{sh}}^{2} \xi + {\text{ch}}^{2} \xi } \right)} \\ \times \left( {\int_{\xi }^{{\xi_{e} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi^{\prime}} \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)\frac{{{\text{ch}}\xi^{\prime } }}{{l\left( {\xi^{\prime } } \right)}}{\text{d}}\xi^{\prime } } } \right){\text{d}}\xi \\ \end{aligned}$$
$$\begin{aligned} B &= \frac{{4x_{\text{f}} p_{\text{sc}} T}}{{\pi T_{\text{sc}} }}\frac{{\beta \rho_{\text{sc}} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{\bar{\mu }h^{2} }}\int_{0}^{{\xi_{\text{e}} }} {\frac{{{\text{ch}}\xi }}{{l^{2} \left( \xi \right)}}\left( {1 - \frac{{{\text{sh}}\left( {2\xi } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)^{2} {\text{d}}\xi } \\ &\quad - \frac{{8x_{\text{f}} p_{\text{sc}} T}}{{\pi T_{\text{sc}} }}\frac{{\beta \rho_{\text{sc}} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{\bar{\mu }h^{2} {\text{sh}}\left( {2\xi_{\text{e}} } \right)}}\int_{0}^{{\xi_{e} }} {\left( {{\text{sh}}^{2} \xi + {\text{ch}}^{2} \xi } \right)} \\ &\quad \times \left( {\int_{\xi }^{{\xi_{\text{e}} }} {\left( {1 - \frac{{{\text{sh}}\left( {2\xi^{\prime } } \right)}}{{{\text{sh}}\left( {2\xi_{\text{e}} } \right)}}} \right)^{2} \frac{{{\text{ch}}\xi^{\prime } }}{{l^{2} \left( {\xi^{\prime } } \right)}}{\text{d}}\xi^{\prime } } } \right){\text{d}}\xi . \\ \end{aligned}$$

Flow inside the fracture

After flowing into the fracture, gas flows to borehole along the fracture. According to the flow formula in fracture, the below equation can be derived through integral calculation.

$$U_{\text{w1}} - U_{\text{w}} = A_{1} q_{\text{sc}} + B_{1} q_{\text{sc}}^{2}$$
(18)

where

$$A_{1} = \frac{{p_{\text{sc}} Tx_{\text{f}} }}{{4k_{\text{f}} T_{\text{sc}} w_{\text{f}} h}};\;B_{1} = \frac{{\beta \rho_{\text{sc}} p_{\text{sc}} Tx_{\text{f}} e^{{\alpha \left( {\bar{p} - p_{0} } \right)}} }}{{16\bar{\mu }T_{\text{sc}} w_{\text{f}}^{2} h^{2} }}.$$

Combining the flow equations outside the fracture, Eq. (17) and inside the fracture, Eq. (18); we can obtain the Eq. (19)

$$\bar{U} - U_{\text{w}} = \left( {A + A_{1} } \right)q_{\text{sc}} + \left( {B + B_{1} } \right)q_{\text{sc}}^{2} .$$
(19)

With Eq. (19), the gas production and the open flow capacity, both taking stress-sensitive permeability into account, are derived respectively as

$$q_{\text{sc}} = \frac{{ - \left( {A + A_{1} } \right) + \sqrt {\left( {A + A_{1} } \right)^{2} + 4\left( {B + B_{1} } \right)\left( {\bar{U} - U_{\text{w}} } \right)} }}{{2\left( {B + B_{1} } \right)}}$$
(20)
$$q_{\text{AOF}} = \frac{{ - \left( {A + A_{1} } \right) + \sqrt {\left( {A + A_{1} } \right)^{2} + 4\left( {B + B_{1} } \right)\bar{U}} }}{{2\left( {B + B_{1} } \right)}}$$
(21)

Applications and discussions

In this section, we programmed by MATLAB to calculate the productivity of fractured vertical gas well via the equations that have been derived above across an instance where the parameters are from a tight gas in china and we also investigated the effects on gas production. The parameters of a certain tight gas in china mainly include initial pressure of 31.889 MPa, bottom-hole pressure of 16.55 MPa, average formation pressure of 31.05 MPa, effective thickness of 18.75 m, initial absolute permeability of 0.089 × 10−3 μm2, formation temperature of 395.6 K, average fluids viscosity of 0.027 mPa s, average gas compressibility factor of 0.89, fracture half-length of 400 m, fracture width of 0.005 m, fracture permeability of 40 μm2, wellbore radius of 0.1015 m, drainage radius of 500 m and stress-sensitive coefficient of 0.01 MPa−1.

Effect of stress-sensitive coefficient on IPR curves

Productivity curves of fractured vertical gas well in different stress-sensitive coefficients are plotted in Fig. 1. From which we can see that as the stress-sensitive coefficients increase, well productivity decreases and the decline rate of gas production is higher, meanwhile the productivity curves bend over to the pressure axis in the earlier stage with a greater bending. This is because the larger stress-sensitive coefficient indicates more intense of stress-sensitive effect to induce more pronounced decrease of permeability with the decline of reservoir pressure, which impacts significantly on well productivity (McKee et al. 1988).

Fig. 1
figure 1

The IPR curves of different stress-sensitive coefficients

Full size image

Effect of matrix permeability on IPR curves

Figure 2 contains productivity curves of fractured vertical gas well in different matrix permeabilities, where the gas production under the bottom-hole pressure of 0 MPa is the absolute open flow. Figure 2 shows that well productivity after fracturing increases apparently with the matrix permeability. The open flow rate is 1.53 × 104 m3/d with the matrix permeability of 0.059 × 10−3 µm2 and increases to 2.52 × 104 m3/d as the matrix permeability up to 0.10 × 10−3 µm2. It indicates that extremely low matrix permeability may lead to a poor gas production that cannot reach the industrial value for exploitation even if fracturing. On the contrary, the stimulation of fracturing has a positive effect in higher matrix permeability. Thus, those gas wells in relatively high matrix permeability should be chosen for fracturing.

Fig. 2
figure 2

The IPR curves of different matrix permeabilities

Full size image

Effects of fracture half-length and conductivity on IPR curves

Productivity curves of fractured vertical gas well with different fracture half-lengths are displayed in Fig. 3 and those with different fracture conductivities are plotted in Fig. 4. In general, Figs. 3 and 4 give the impressions that gas production has a positive relation with the fracture half-length and conductivity. The increase of gas production is non-linear with the linear variations of fracture half-length and conductivity. It is significant that the increment of gas production gradually ascends with the fracture half-length but descends with the fracture conductivity. Namely, increasing fracture half-length could more benefit the gas production than increasing the fracture conductivity.

Fig. 3
figure 3

The IPR curves of different fracture half-lengths

Full size image
Fig. 4
figure 4

The IPR curves of different fracture conductivities

Full size image

Effects of the factors on open flow

The effects of stress-sensitive coefficient, matrix permeability, fracture half-length and conductivity on the open flow capacity of gas well are investigated. The analysis is shown in Table 1. It demonstrates that stress-sensitive coefficient, matrix permeability, fracture half-length and conductivity impact the open flow in varying degrees. Open flow has a positive correlation with matrix permeability, fracture half-length and conductivity, but a negative relation with stress-sensitive coefficient. In these factors we investigated, matrix permeability and fracture half-length lead the first and second place for most affecting the open flow, respectively. Meanwhile, fracture conductivity contributes the slightest impact on gas production. Thereby, an instruction is drawn that the longer fracture half-length and the choosing of gas well in favorable geological condition are primary for fracturing stimulation.

Table 1 The open flow capacity of gas well with different sensitive parameters
Full size table

Conclusions

Productivity equations in pseudo-steady state for fractured vertical gas well embedded with the stress-sensitive effect have been derived and applied across an instance. And the effects of stress-sensitive coefficient, matrix permeability, fracture half-length and conductivity on gas production have been investigated, which draws a significant instruction for fracturing stimulation. Gas production and open flow are affected in different extents by stress-sensitive coefficient, matrix permeability, fracture half-length and conductivity. They are positively correlative with matrix permeability, fracture half-length and conductivity, but negatively related with stress-sensitive coefficient. In the factors we investigated, matrix permeability leads the list of the effects on gas production and open flow. The gas well in extremely low-permeability area cannot achieve the production of industrial value for exploitation even after fracturing unless multistage fracturing was conducted or complicated fractures were generated.