Modeling of BHA dynamic behaviors

Abstract

Lateral and torsional vibrations of drill strings used in oil well operations are considered. This work presents finite-element-based bottom hole assembly model which addresses natural frequencies determination, and torsional and lateral oscillations on the near vertical well. In terms of the excitations of the developed finite-element model, forces are applied on the bit with time history generated using an Auto-Regressive Moving-Average digital filter. Due to the random pattern of the forces at the drill bit, a stochastic dynamic approach is adopted in investigating the problem. The method of Newmark-beta direct integration is used. It is hoped that this study will enhance the interest in using stochastic dynamic techniques in drilling system analysis and design, as they can capture quite appropriately the inherent uncertainty of the bit forces and, potentially, of other sources. The implementation of torsional degree of freedom during the development of MATLAB code has been considered new attribute regarding previous works based on the same research line. The results from the code developed attained a good agreement with the commercial SPA2000 Advanced 14.0.0 Structural Analysis Program software.

Introduction

In the type of deep drilling operations that are commonly used for hydrocarbon exploration and recovery, there are a few common designs. These drilling operations typically make use of drill strings, which are pipes that transmit both drilling fluid and torque necessary to rotate a drill bit. The top end of a drilling string typically has the machinery necessary to pump the drilling fluid, and either a top or kelly drive to provide torque for the drill bit. Pipe typically encases the string below, to contain the drilling fluid. The lower end of the string, consisting of the drill bit, collars and other components that are collectively known as the bottom hole assembly (BHA), is the region of many failures (Macdonald and Bjune 2007). Typical problems that are encountered include severe stick–slip, lateral vibration, hole enlargement, which induce poor directional control. Inevitably this problem causes costly drilling equipment failures.

Development of downhole measurement technique with high frequency resolution has helped appreciating the significance of these vibrations and their impact on equipment failure. Providing consistent and reliable time histories, which are used to study random vibration on drill string, is always of great importance. These problems include random loading force and acceleration at the bit and random formation contact properties. A general vibration perspective of the oil and gas drilling process can be found in Spanos et al. (2003).

One approach to reduce the cost associated with the failures is to use BHA dynamic simulation software and preemptively mitigate the anticipated problems. The ability to pinpoint the source and effects of torsional, axial and lateral oscillations enables users to qualify design changes to the drill-string configuration and optimize parameters, prior to drilling the well, thus minimizing the traditional “trial” and “error” approach and operator risk.

More recently, nonlinear and time-domain modeling solutions have become possible (Spanos et al. 2002). This is critical to achieve the required level of accuracy to make meaningful contributions to drilling system behavioral prediction. While the finite-element method has been used for a number of years in the oilfield, it has been limited to sections of the drill string or discrete components. Simulations for the entire drilling system are exceptionally time consuming and complex both in setup and computational time. These factors are considered when planning the length of drilling intervals to be analyzed.

The paper pursues an analysis of the drill-string dynamic nonlinear problem by resorting to finite-element modeling of the string and using the Newmark-beta direct integration and Monte Carlo simulations to capture the salient features of the problem.

Dynamic modeling of the drill string

A drill string on a drilling rig is primarily composed of drill pipe, drill collars and drill bit. Its function is to convey drilling fluid (via the mud pumps) and torque (via the kelly drive or top drive) to the drill bit. The drill string is hollow so that drilling fluid can be pumped down through it and circulated back up the annulus, creating clearance between the drill string and the casing/open hole (ASME 2011). A typical drill string can extend over several kilometers.

The BHA is made of a drill bit, which is used to break up the rock formations, drill collars, which are heavy, thick-walled tubes used to apply weight to the drill bit and drilling stabilizers, which keep the assembly centered in the hole. The BHA may also contain other components such as a downhole motor and Rotary steerable system, measurement while drilling (MWD) and logging while drilling (LWD) tools. The components are joined together using rugged threaded connections. Short “subs” are used to connect items with dissimilar threads (Chevallier 2000).

Drill pipe makes up the majority of the drill string back up to the surface. Each segment has a larger diameter portion on each end containing a male (“pin”) or female (“box”) thread. The major objective of this article was to describe the dynamic behavioral response of BHA subjected to deterministic and stochastic excitations. Two major types of bits are used: roller cone (RC) bit (Fig. 1) and polycrystalline diamond compact (PDC) bit (Fig. 2).

Fig. 1

Roller Cone (RC) Bit. Courtesy of Schlumberger

Fig. 2

Polycrystalline Diamond Compact (PDC) Bit. Courtesy of Schlumberger

A complete description of the dynamic behavior of a BHA requires three displacements and three rotations assigned at each node. This model is more accurate than certain simplified models which describe only specific vibration modes. Nevertheless, a complete finite-element model demands more computational power. In order to reduce the computational effort and facilitate the interpretation of the numerical results, only lateral and torsional vibrations are examined herein (Chevallier 2000).

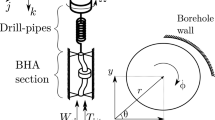
A particular drill string for a near vertical well is considered (Tables 1, 2). The drill string is modeled as a beam discretized within several finite elements. The BHA is clamped on the top and free on its other end. Further the stabilizers are pinned, that is, their lateral displacement is restricted. The lateral force is applied on the free drilling bit. All the parts of the BHA are made of the same material and are represented by linear elements of equal length. No compressive force, which represents the weight on bit (WOB), is applied on the drill pipe only from drill pipe. Each node of the finite element has three degrees of freedom: lateral displacement, angular displacement and torsional displacement, and it is a two-dimensional problem. A clearance of 10 cm between wellbore and BHA is assumed. To formulate a continuous model, the Euler–Bernoulli beam theory is considered, and a small-slope assumption is adopted (Aadnoy et al. 2009). The resulting system of equations of motion for the BHA is captured by the MDOF model (Chevallier 2000):

$$\mathbf{M}\ddot{\mathbf{u}}(t)+\mathbf{C}\dot{\mathbf{u}}(t)+\mathbf{Ku}(t)=\mathbf{g}(t),$$

(1)

where $\mathbf{M},\mathbf{C}$ and $\mathbf{K}$ are matrices that hold information pertaining to mass, dampening and spring/elasticity coefficients for the node in question. The damping matrix, $\mathbf{C}=\mathit{\alpha }\mathbf{M}+\mathit{\beta }\mathbf{K}$, is a linear combination of the system mass and stiffness matrices by means of Rayleigh coefficients $\mathit{\alpha }$ and $\mathit{\beta }$, which are appropriately selected to yield meaningful modal damping. The coefficients $\mathit{\alpha }$ and $\mathit{\beta }$ are set as 0.01 and 0.001, respectively. The vector function $\mathbf{g}(t)$ characterizes the lateral excitation applied to the system and $\ddot{\mathbf{u}}(t),\dot{\mathbf{u}}(t),\mathbf{u}(t)$ characterize the displacement, velocity and acceleration, respectively.

Table 1 Geometrical properties of the BHA

Table 2 Material properties of the BHA

The well borehole is accounted for as shown in Fig. 3. The BHA lateral displacement is unconstrained until a clearance value $\mathit{\alpha }$ is exceeded (Aadnoy et al. 2009). For nodes with lateral displacement of magnitude larger than $\mathit{\alpha }$, an additional spring is activated to model contact with the wall. A Hertzian contact law is assumed, described by the following equation:

$$F_i(\mathbf{u}(t))=\left\{\begin{array}{c}-k_2\left(-u_i(t)-\mathit{\alpha }\right),u_i\le -\mathit{\alpha }\\ 0,-\mathit{\alpha }\le u_i\le \mathit{\alpha }\\ k_2\left(u_i(t)-\mathit{\alpha }\right),u_i\ge -\mathit{\alpha }\end{array}\right.$$

(2)

where $F_i,i=1,3,5,\dots N,$ is the $i$ component of the vector function $\mathbf{F}(\mathbf{u}(t))$ characterized by an influence of the rock through the borehole presence acting as a restoring force, $u_i(t)$ is the magnitude of the $i$ component of the lateral generalized displacement vector u, the coefficient $k_2$ is the rock stiffness coefficient and $N$ is the total number of degrees of freedom of the mathematical model (Spanos et al. 1997; Santos 2011). Incorporating Eq. (2) into (1) yields

$$\mathbf{M}\ddot{\mathbf{u}}(t)+\mathbf{C}\dot{\mathbf{u}}(t)+\mathbf{Ku}(t)+\mathbf{F}(\mathbf{u}(t))=\mathbf{g}(t).$$

(3)

To solve Eq. (3) we consider the following Cauchy data,

$$\mathbf{u}(0)={\mathbf{u}}_0,\dot{\mathbf{u}}(0)={\mathbf{u}}_1,$$

(4)

where ${\mathbf{u}}_0,{\mathbf{u}}_1$ are known vectors, defining the initial state of the system.

Fig. 3

BHA finite-element model for lateral considering well borehole contact. Excerpted from IADC/SPE 23905

The lateral excitation of the BHA depends strongly on the kind of the drill bit applied to drilling operation. The RC bit and PDC bit differ in their frequency content, as the excitations induced by RC bits tend to possess significant levels of energy over a determined range, whereas PDC bits produce excitations of frequency content centered at the rotational driving frequency (Chevallier 2000).

This is due to the fact that the RC bit crushes the rock by abrasion of the protruding elements which are uniformly distributed on the rotating cones, as compared to the PDC bit in which the rock crushing involves protruding elements which are stationary with respect to the drill string and thus induce excitation associated primarily with the rotary speed of the bit. In this context, excitations induced by RC bits are modeled by band-limited white noise, as shown in Fig. 4. Furthermore, lateral excitations induced by PDC bits are modeled by Kanai Tajimi power spectrum as shown in Fig. 5. The Cauchy problem (3) and (4) is solved in its discrete form by means of Newmark-beta direct integration associated with Monte Carlo simulation (Chevallier 2000).

Fig. 4

Lateral power spectrum excitation for RC Bit

Fig. 5

Lateral power spectrum excitation for PDC Bit

The approach adopted for the Newmark-beta method in this study was the average acceleration scheme based on the trapezoidal rule in which the acceleration during a time interval $t_n$ to $t_{n+1}=t_n+\mathrm{\Delta }t$ is approximated as the average of its initial and final values as follows:

$$\ddot{\mathbf{u}}(\mathit{\tau })=\frac{\ddot{\mathbf{u}}(t_n)+\ddot{\mathbf{u}}(t_{n+1})}{2}.$$

The time step $\mathrm{\Delta }t$ must be selected so that both the smallest period of the excitation and the natural period of system may be represented adequately. A proper choice of the time interval yields a good approximation of the exact solution.

The random excitations are a set of time histories generated by means of an ARMA algorithm, each of which possesses a determined number of points (Spanos 1983; Spanos et al. 1990; Spanos and Zeldin 1998). For each excitation, the governing dynamic equation of motion provides a different response, in this regard, the simulated responses are submitted to a statistical treatment. The statistical properties of the response are computed as ensemble averages over the simulated responses. This procedure is a simple application of Monte Carlo simulations technique (Chevallier 2000). The time-domain solution with Monte Carlo simulations is based on solving a set of deterministic problems. The statistical characteristics of the excitation, such as its power spectral density, permit generating a set of compatible time histories. These are deterministic since each one represents a particular realization of the random excitation function. The response of the finite-element BHA to each realization can therefore be computed.

Upon having derived the solution to each deterministic time histories, ensemble characteristics of the group of responses can be computed, yielding the statistical properties of the response. In this regard, the major phase in this procedure is to obtain the time-domain response of a nonlinear system to a deterministic excitation.

It is important to mention that the proposed mathematical model herein developed for this study does not take into account the hydraulic effects, friction between the BHA components and the formation, reactive torque from the bit and BHA components with formation, drill string torque, well tortuosity, cutting effect, drag forces among other well complexities all of which may most likely degrade the model accuracy once the numerical results are compared against the real field data. For this study, the input data were from previous published academic articles so as to illustrate and validate the methodology.

Numerical results

As an illustration, for this numerical application, the stochastic downhole force, i.e., lateral excitations, applied at the bit node and only assigned at the lateral degree of freedom will be associated for a roller cone bit. To this end, time histories compatible with the power spectrum corresponding to the roller cone bit are generated by means of an ARMA algorithm. A set of 100 time histories, each of which possesses 500 data points, is generated. The generated time histories are then used as excitations for the system, being applied at the node which represents the drill bit solely.

Figures 6, 7, 8, 9 show the numerical results concerning stochastic downhole forcing function for a roller cone bit considering interaction between the wellbore and BHA based on Hertz’s contact law and without considering torsional degree of freedom. The first four numerical responses are presented for acceleration, velocity and displacement, in which each response is associated with different excitations, therefore, proving that each excitation generates different responses and so the time-domain solution with Monte Carlo simulations is based on solving a set of deterministic problems.

Fig. 6

Lateral displacement of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 7

Lateral velocity of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 8

Lateral acceleration of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 9

Probability density function of the displacement of the roller cone bit for a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Figures 10, 11, 12, 13 show the numerical results concerning stochastic downhole forcing function for a roller cone bit considering interaction between the wellbore and BHA based on Hertz’s contact law and torsional degree of freedom. The first four numerical responses for acceleration, velocity and displacement are presented.

Fig. 10

Lateral displacement of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 11

Lateral velocity of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 12

Lateral acceleration of the BHA subjected to a stochastic downhole forcing function for a roller cone and a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

Fig. 13

Probability density function of the displacement of the roller cone bit for a rock stiffness, k₂, equivalent to 1.51E+06 N m^−3/2

In order to validate the numerical results obtained from the MATLAB software developed for this research, an ordinary BHA subjected to a harmonic co-sinusoidal forcing function was run on commercial software, SPA2000 Advanced 14.0.0 Structural Analysis Program, and a good agreement was attained, as can be seen in Figs. 14, 15, 16 and 17.

Fig. 14

Lateral displacement from MATLAB simulation of an ordinary BHA subjected to a harmonic co-sinusoidal forcing function, whose excitation frequency and lateral harmonic excitation of magnitude are 2π rad s⁻¹ and 100 m, respectively

Fig. 15

Lateral displacement from SPA2000 simulation of an ordinary BHA subjected to a harmonic co-sinusoidal forcing function, whose excitation frequency and lateral harmonic excitation of magnitude are 2π rad s⁻¹ and 100 m, respectively

Fig. 16

Lateral displacement from SPA2000 simulation of an ordinary BHA subjected to a harmonic co-sinusoidal forcing function, whose excitation frequency and lateral harmonic excitation of magnitude are 2π rad s⁻¹ and 1,000 m, respectively

Fig. 17

Lateral displacement from MATLAB simulation of an ordinary BHA subjected to a harmonic co-sinusoidal forcing function, whose excitation frequency and lateral harmonic excitation of magnitude are 2π rad s⁻¹ and 1,000 m, respectively

Figures 15 and 16 represent the numerical result generated from commercial software aforementioned adopted on this work as a reference according to aforementioned. The x and y axes in these figures denote the time in seconds and amplitude magnitude in meters, respectively.

Summary and conclusions

A finite-element model has been used to study the dynamic behavior of the BHA subjected to stochastic excitations. The dynamic response of the BHA has been attained by means of a Newmark-beta direct interaction for two different types of drill bit.

In order to obtain the probability density function of the displacement, Monte Carlo simulation was used. The mathematical model herein developed is able to predict the critical speed range in which the rotary BHA for a near vertical well can potentially experience natural frequency-induced vibrations, and foresee the dynamic rotary BHA response for either PDC or RC bit in terms of lateral and torsional vibrations for a specific applied WOB and rock stiffness coefficient within a drilling scenario.

In this sense, the user is able to filter out the drilling parameters, i.e., RPM and WOB, prone to resonance effects, and detrimental lateral and torsional vibrations based on the material and geometrical properties, applied WOB and rock stiffness coefficient. It is worth beholding the effect of torsional degree of freedom on the BHA response once it has been implemented to the model, the torsional degree of freedom added more inertia to the system, yielding a slight reduction on the magnitude of output results.

By beholding Figs. 14, 15, 16, 17, wherein an ordinary BHA has been simulated subjected to a deterministic excitation applied at the bit node, it is clearly noticeable that the numerical results from finite-element model in conjunction with the Signal Processing algorithm developed on MATLAB for this academic study had a good agreement with the commercial software, SPA2000, with minimal error, validating therefore the mathematical model herein presented.