Introduction

Finding the most prospective areas or “sweet spots” in any reservoir, and aligning the wellbore to be exposed to these zones are amongst the key factors for successful field development. In unconventional reservoirs, this means locating the well in an area and direction that will allow generation of conductive fracture networks during hydraulic fracturing. These geomechanical sweet spots are controlled by current day in situ stresses, ancient stresses, and pre-existing natural fractures.

Modelling present in situ stress tensors, pore pressure, and mechanical properties of the rocks are essential for locating sweet spots (Norberto et al. 2007; Zoback 2010). One of the biggest challenges in this procedure is to be able to model the heterogeneity of rock mechanical properties for better understanding of rock behaviour during hydraulic fracturing. Our first approach in this study is to determine magnitudes and orientations of present day in situ stresses and pore pressure, interpret faults and horizons from 3D seismic in depth, and to use computer models to apply these stresses on the existing structures. This will help predict stress at locations with no available direct stress measurements, and thus locate possible sweet spots.

Rocks may have been subjected to tremendous diversity of stress magnitudes and orientations during tectonic history which might have caused rock failure and generated fractures. Some of these paleo-stresses might have been stored in the rock masses (Angelier 1994) and are influencing the behaviour of rocks and thus the location of sweet spots. Another approach used in this study is stress inversion (Gapais et al. 2000; Lisle et al. 2001; Orife and Lisle 2003). The methodology utilizes fault slips calculated from interpreted faults and horizons on 3D seismic to restore the initial state of the rock body in question while considering geomechanical properties, then forward modelling and calculating the paleostresses resulted from various tectonic events. Spatial distribution of these stresses is going to be examined for possible locations of sweet spots.

Direct mapping of pre-existing natural fractures using seismic attributes may also be useful for locating sweet spots but not the focus of this study. Some efforts done in this field can be found in the work of Backé et al. (2011) and Abul Khair et al. (2012).

Researches previously conducted using similar approaches concentrated on calculating in situ stresses (e.g., Reynolds et al. 2004), mapping the effect of lithology and faults characteristics on stress distribution around fault tips (e.g., Karatela 2012), relating displacement of strata to fault geometry and loading conditions (e.g., Hilley et al. 2010; Maerten and Maerten 2008; Tamagawa and Pollard 2008; Maerten and Maerten 2006; Thomas 1993), and applying stress inversion on specific case studies to understand the tectonic history (e.g., McFarland et al. 2012; Vidal-Royo et al. 2011). Our study will focus on applying the present day and paleo-stress calculations on the Cooper Basin and compare the results to imaged fractures and gas production rates for validating their use to locate unconventional sweet spots.

Geologic and tectonic setting of the Cooper Basin

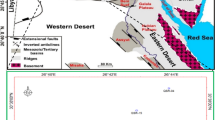
The Cooper Basin is a Late Carboniferous to Middle Triassic basin located in the eastern part of central Australia (Fig. 1). The Cooper Basin floor was curved out of the uplifted topography following the formation of Warburton Basin. The sedimentary basins within the interior of the Australian continent have been subject to several tectonic events resulting in periods of subsidence, inversion, and uplift, from the Neoproterozoic until the present day (Preiss 2000; Backe et al. 2010).

Fig. 1
figure 1

Top Warburton Basin (Pre-Permian Basement, seismic horizon Z) in the Cooper Basin (Modified after NGMA, 2009). Map shows NE–SW major troughs separated by ridges. Study area is located at the south-western termination of the Nappamerri trough (Moomba-Big Lake 3D seismic cube outlined in yellow). A Innamincka Ridge; B Murteree Ridge; C Gidgealpa-Merrimelia Ridge; Wooloo Trough; E Della-Nappacoongee Ridge; F Allunga Trough; H Warra Ridge. Top left: Australian stress map (Modified after Hillis and Reynolds, 2000 and World Stress Map, 2008), Shmax indicated in black lines

Full size image

Following the deposition of the Cambrian–Ordovician sequences of the eastern Warburton Basin underlying the Cooper Basin, NW–SE compression caused a partial inversion of the Warburton Basin, deformation of the pre-existing sequence and the subsequent intrusion of Middle to Late Carboniferous granites (Gatehouse et al. 1995; Gravestock and Flint 1995; Alexander and Jensen-Schmidt 1996). This tectonic event is coeval with the Alice Springs and Kanimblan Orogenies, which affected Central Australia.

The Early Permian sequences of the Cooper Basin sediments were deposited in an environment largely controlled by Gondwanian glaciations (Powell and Veevers 1987; Fig. 2). The depositional environment was controlled by highly sinuous fluvial system flowing northward over a floodplain with peat swamps, lakes and gentle uplands (Apak et al. 1993, 1995, 1997). The remaining Cooper Basin sediments were deposited during a period of tectonic quiescence, within an open basin environment with restricted access to the sea from the east followed by a meandering fluvial system (Stuart 1976; Thornton 1979). A basin-wide erosional unconformity marks the end of the Permo-Triassic Cooper Basin sediments due to the Hunter-Bowen Orogeny (Wiltshire 1982), this shifted the depocentre northwest and triggered the formation of Eromanga Basin.

Fig. 2
figure 2

Stratigraphy and paleo-stress directions of the Cooper Basin (Modified after Gravestock et al. 1998)

Full size image

Data and methodology

This study focusses on the Moomba-Big Lake fields, which are located at the south western termination of the Nappamerri Trough in the Cooper Basin (Fig. 1). The area is covered by a 3D seismic survey across ~ 800 km2 and drilled by 300 oil and gas wells ranging in depths between 1,790 and 3,700 m. Of these wells, twenty-nine wells have check shots that allow the seismic data interpretation to be tied to the geology. Most of these wells contain wireline logs, seven contain image logs, and a large number of wells have recorded drill stem tests (DST), repeated formation tests (RFT), leak off tests (LOT), and hydraulic fracture tests mostly for Patchawarra and Toolachee formations. Some wells contain these tests within the shale horizons or the deeper sequences.

Seven horizons were interpreted within the Moomba-Big Lake 3D seismic survey (Toolachee, Daralingie, Roseneath, Murteree, Patchawarra formations, and the VC50, a strong coal reflector within Patchawarra Formation; Fig. 2). Also, a shallow sandstone formation from Eromanga Basin sediments (Hutton Formation) was interpreted to simulate the real earth. Structural interpretation and seismic attributes were used to identify large-scale faulting trends and possible fracture network within the survey. The Cooper Basin formations are considered unconventional reservoirs as the gas and oil produced in the basin are either from shales or tight sands.

Pore pressures were taken from DSTs and RFTs, where available. For intervals without these required data, the pressure from both Bowers (1995; Eq. 1) and Eaton (1972 and 1975; Eqs. 2, 4 and 5) methods were generated and compared. Calculation of pore pressure from these equations was done for intervals with available reservoir pressure tests to validate the methodologies and choose the more reliable method.

The Bowers (1995) method uses the equation:

$$\sigma \prime = \{ (v - v_{0} )/A\}^{1/B}$$
(1)

where \(\sigma \prime\) is vertical effective stress, v is P wave interval velocity picked from the check shots, \(v_{0}\) is the velocity at zero effective stress, and A and B are parameters. \(v_{0}\) is used as 5,000 ft/s (1,524 m/s) most of the time and rarely picked from the check shots. A and B were chosen from the ‘best fit’ parameters estimated by Gutierrez et al. (2006) to be A = 9.18448, B = 0.764984.

The Eaton (1972, 1975) method of predicting pore pressure is based on the equations:

$$\sigma \prime = \sigma \prime_{\text{normal}} \left( {v/v_{\text{normal}} } \right)^{3}$$
(2)

where σ′normal is calculated by multiplying the vertical depth by the normal vertical effective stress gradient (0.57 psi/ft = 12.9 kPa/m). vnormal is calculated from Xu et al. (1993):

$$v_{\text{normal}} \left( z \right) = v_{0} + \, kz$$
(3)

where k is the vertical velocity gradient and lies in the range of 0.6–1.0 S−1, and z is the depth. In the studied wells, k was calculated and was found to be 1 for most of the wells.

$$\sigma \prime = \sigma \prime_{\text{normal}} \left( {v/v_{\text{normal}} } \right)^{b}$$
(4)

The value of b was chosen to be 2.3285, which is the best fitting parameter according to Gutierrez et al. (2006).

$$\sigma \prime = \sigma \prime_{\text{normal}} a\left( {v/v_{\text{normal}} } \right)^{b}$$
(5)

where a and b are parameters and were chosen to be a = 0.785213, b = 1.49683, which are the best fitting parameters according to Gutierrez et al. (2006).

The vertical or overburden stress Sv at a specific depth can be determined from the pressure exerted by the weight of the overlying rocks using the integration of density logs from petroleum wells (Jaeger and Cook 1979):

$${\text{Sv}} = \mathop \int \limits_{0}^{z} \rho \left( {\text{z}} \right){\text{gdz}}$$
(6)

where ρ(z) is the density at depth z below the surface, and g the acceleration due to gravity. The density of the overburden was estimated using the density logs for the interval that contained density logs. As density logs are not often run from surface, we calculated the density from the interval velocity using the relation of Gardner et al. (1974), which relates density to interval velocity, where there are no density logs. The formula of Gardner et al. (1974) that relates density to velocity is as follows:

$$\rho = a\upsilon^{b}$$
(7)

where ρ is density, υ is velocity, and a and b are parameters. The best fitting parameters according to Gardner et al. (1974) are a = 0.23, and b = 0.25.

Pore pressure ρp was estimated using the relation of Gardner et al. (1974):

$$\rho_{\text{p}} = {\text{Sv}} - \sigma \prime$$
(8)

Although these methodologies for calculating pore pressure were developed for passive margins where the maximum principal stress is mostly the vertical, a validation check was conducted in areas with directly measured pore pressure and negligible error was found.

In-situ stress magnitudes and orientations

The magnitude of minimum horizontal stress (Shmin) was estimated from both hydraulic fracture tests and LOTs. The lower bound to leak-off pressures in vertical wells gives a reasonable estimate of the minimum horizontal stress magnitude when the minimum horizontal stress is the minimum principal stress (e.g., Breckels and van Eekelen 1982; Bell 1990). As no indication of reverse stress regime was found in the study area, this assumption is valid and is used in the current study. The magnitude of the maximum horizontal stress (Shmax) is constrained by assuming that the ratio of the maximum to minimum effective stress cannot exceed that required to cause faulting on an optimally oriented pre-existing fault (Sibson 1974). The frictional limit to stress is given by the following equation (Zoback 2010):

$$\frac{{S1 - P{\text{p}}}}{{S3 - P{\text{p}}}} \le \{ \surd (\mu^{2} + 1) + \mu \}^{2}$$
(9)

where μ is the coefficient of friction on an optimally oriented pre-existing fault, S1 is the maximum principal stress, S3 is the minimum principal stress and Pp is the pore pressure. Empirical analysis conducted by Zoback and Healy (1984), showed that this relation can be used in seismically active regions with the typical value of μ = 0.6 for strike slip stress regimes (which is the stress regime in the Cooper Basin and will be discussed in details later). When μ = 0.6, then Eq. 9 reduces to:

$$\frac{{S1 - P{\text{p}}}}{{S3 - P{\text{p}}}} \le 3.12$$
(10)

The orientations of Shmax and Shmin have been estimated using the interpretation of resistivity images of borehole walls produced by the Formation Micro Scanner (FMS) tool. In total, we interpreted more than 104 breakouts and 29 drilling induced tensile fractures (DITFs) from seven wells drilled in the Moomba-BigLake area.

We used borehole breakouts and Drilling Induced Tensile Fractures (DITFs) observed on image logs to determine orientations of the three principal stresses. In the Earth’s crust, the three principal stresses can be resolved into a vertical and two horizontals stresses, considering that the earth`s surface is a free surface (Anderson 1951).

When the circumferential stress acting around a wellbore exceeds the compressive strength of the rock in a vertical well, conjugate shear fractures form at the wellbore wall centred on the minimum horizontal stress direction, causing the rock to spall off (Bell 1979). As a result, the wellbore becomes enlarged in the minimum horizontal stress direction, which forms the wellbore breakouts. Borehole breakouts form perpendicular to the present-day Shmax orientation and appear on image logs as dark conductive areas separated by 180° (Kirsch 1898; Bell 1979, Zoback 2010).

DITFs form parallel to the present-day Shmax in vertical wells and appear on image logs as dark conductive fractures separated by 180°. DITFs are different from pre-existing natural fractures in many aspects: on image logs, DITFs are not longer than 2 m, often contain small jogs or kinks, discontinuous, and appear as dark, electrically conductive fractures. In contrast, natural fractures appear as continuous sinusoids, and can be conductive or resistive (Barton and Zoback 2000). Both borehole breakouts and DITFs appear on image logs separated from each other by 90° (Fig. 3). Our analyses of the interpreted breakouts and drilling-induced tensile fractures show an average Shmax direction trending at N101°E (Table 1). This is consistent with a previous basin-wide study conducted by Reynolds et al. (2004) using wells DITFs and breakouts, which gave a Shmax orientation of N 101°, as interpreted from compiled data across the whole of the Cooper Basin.

Fig. 3
figure 3

Electrically conductive breakouts and drilling induced fractures in Big Lake 54. Lower picture shows the direction of the measured breakouts along the well

Full size image
Table 1 Number of borehole breakouts and drilling-induced tensile fractures recorded in each well
Full size table

The calculated magnitudes of the three principal stresses in the Moomba-Big Lake fields resulted that Shmax was found to be the maximum principal stress and the magnitude of the vertical stress was found to be greater than the minimum horizontal stress, thus, a strike-slip stress regime (Shmax > Sv > Shmin) dominates the field (Fig. 4). This result is consistent with the results of Reynolds et al. (2004). The former author showed that the stress regime changes with depth to reverse fault stress regime. The current study did not show this change as the available data do not cover deep intervals when compared with other parts of the basin.

Fig. 4
figure 4

Stress magnitude verse depth plot of the Moomba-Big Lake field. S v vertical stress, Sh max maximum horizontal stress, Sh min minimum horizontal stress

Full size image

Geomechanical model of current day stress

3D geomechanical models of friction and slip along faults can be used to estimate deformation, displacements (faults and fractures) and current day stress (Maerten 2000; Dair and Cooke 2010). Although frictional slip along faults control fracture orientations (Auzias 1995; Ohlmacher and Aydin 1997), seismic cycle (Tse and Rice 1986), quantitative and spatial slip distribution along faults (Burgmann and Pollard 1994), and frictional slip along bedding planes affect faults and fractures propagation, current 3D models solve for frictionless faults as computation using frictional sliding along contacts is hard to be implemented (Maerten et al. 2010).

The boundary element method (BEM) is one numerical method for modelling crustal deformation and is used in the current study. The BEM method needs only to know about the boundaries of an object rather than the whole object. The focus on the boundaries instead of the body (as in the finite element method) gives BEM a fast solution at the cost of limited model complexity. The BEM software used in this study is Poly3D and is described in detail by Maerten and Maerten (2008).

Poly3D solves for angular dislocation in an elastic half-space as described by Comninou and Dundurs (1975). It constructs a polygonal element as a sum of two angular dislocation segments (Maerten et al. 2010), then calculates the displacements, strains and stresses at every observation point within the elastic field using the current state of stress magnitudes and orientations and pore pressure (Thomas 1993). The user has the ability to assign flat observation grids to display the results, but in this study the interpreted horizons in the model were chosen as observation grids to be able to display the computed results at the horizons rather than at flat grids.

Boundary conditions (BCs) used for the faults within the model include allowing the faults to slide in the dip and strike direction without any fault normal component. No fluid pressure was used within the faults zones. Due to the complexity of computation using frictional sliding, no friction coefficient or cohesion was assigned for the faults and the fault system was considered frictionless.

Far field stresses were assigned to the model using the stress values and orientations described earlier in this paper. Stress gradients of 27.5, 15.6, and 22.9 MPa/km were used for the maximum horizontal stress, minimum horizontal stress, and vertical stress, respectively, with a pore pressure gradient of 10 MPa/km. As the Cooper Basin sequence is mainly an alternation of sandstones and shale horizons, rock elastic properties used for this study are listed in Table 2 which comprises the average rock properties for both types of lithology. Although porosity appears to be high compared with measured reservoir porosity, a porosity sensitivity check was conducted and negligible changes in resulted stresses and strains were found.

Table 2 Rock mechanical properties used as input for modelling stress perturbation around structural features
Full size table

The resulted stress perturbation around Big Lake fault (Fig. 5) shows a low value of minimum effective stress in the middle part of the fault at the Big Lake field side (arrow in Fig. 5a, b). The low magnitudes of minimum horizontal stress indicate less pressure required for hydraulic fracturing (i.e., fracture stimulation sweet spots). As the productive Cooper Basin formations are either shales or tight sands, they all underwent fracture stimulation. Thus, low magnitudes of Shmin indicate better fracture stimulation, and most likely, better production. Poly3D also predicts the orientation of natural fractures from current day stress (not shown in this paper). A conjugate set, which trends N70E and N130E, were found with minor reorientation close to faults.

Fig. 5
figure 5

Map view of minimum effective stress distribution around Big Lake fault due to the effect of the present stress magnitudes and orientation for a Patchawarra formation, b Toolachee formation. Blue colour in the Big Lake field (arrow) shows the main producing area in the field

Full size image

Geomechanical model of paleo-stresses

Over the past century, structural geologists have invested considerable effort in relating stress and fault slip to tectonic history (Price 1966; Mandl 1988). They used both forward and inverse modelling to solve these relationships. In forward modelling, the tectonic stresses are assumed to be homogeneous and described as boundary conditions acting at some distance from the faulted rock (Hafner 1951; Couples 1977; Maerten et al. 1999). In inverse modelling, the stress tensor is deduced from the existing geological structure (e.g., folds), plus an interpretation of fault slip (see Carey and Burnier 1974 and Kaven et al. 2011 for more details).

The method of stress inversion was first introduced by Wallace (1951) and Bott (1959) who assumed that the remote stress tensor is spatially uniform for the faulted rock and constant during the fault history, and the slip along any fault is in the same direction and sense of the maximum shear stress. These assumptions generated encouraging results and cleared the way for further usage and improvement of the technique (Pollard et al. 1993). By knowing fault orientation and slip, inversion methods are able to estimate paleo-stresses that caused these movements, and to predict the most likely generated structures assuming some user-supplied rock properties. These methods are the foundation for the numerous computer models that predict paleo-stresses and the resulting faults and fractures.

3D restoration and stress–strain–displacement calculation using stress inversion and forward modelling is becoming more common for unravelling geological history. Several codes are available for restoring and forward modelling geological structures, each with different input parameters and different solvers. Two common solvers used in the restoration procedure are the FEM and the BEM. The application of each methodology in the current study will be discussed in detail in the following.

Dynel3D (Finite element method (FEM))

FEM is a numerical method for problem solving that has a big advantage over the BEM in that it can describe quite complex distributions of rock properties. In FEM, the whole object is discretised and each element will have a simpler approximation of the solution which will be joined later with other elements of the same object to form the global solution (Hughes 1987).

In the current study, we used a code called Dynel3D which utilizes geomechanics in restoring geological structures considering the physical laws (including conservation of momentum, mass and energy) and using the linear elastic theory. Stresses that cause permanent deformation are not considered in this code. Each element is assigned material properties which might differ vertically from other elements. If deformation exists, the code uses a solver that allows forces to be transmitted from node to node until equilibrium is obtained (Maerten and Maerten 2006).

Dynel3D’s methodology calculates stresses at the time of faulting and folding using input seismic structural interpretation and rock properties. The estimated stresses plus user-supplied rock failure criteria are used to predict fractures. Dynel3D models the behaviour of folded, fractured and faulted heterogeneous, anisotropic, and discontinuous mediums (Maerten and Maerten 2006). Within this code, the structural model is discretised with 3D tetrahedral elements which form the mesh of the studied structure.

Dynel3D assumes linear elasticity for structural restoration. This assumption is a potential pitfall, but it allows for a simpler and faster solution. Advantages of Dynel3D include the ability to model vertical heterogeneity in rock mechanical properties, ability to use friction in modelling faults, and applicability to any stress regime (Maerten and Maerten 2006).

We applied the geomechanical restoration technique using the FEM solver in Dynel3D for the Moomba-Big Lake structural model. The software calculates the stress, strain, displacement, and effective stress on every node of the mesh elements within the input target horizons (Fig. 6). Rock elastic properties were assigned to the shale and sandstone horizons within the Cooper Basin sequence as listed in Table 2. Restoration for every horizon was conducted to the altitude of the highest point within the same horizon. No sliding was allowed between the horizons and they were constrained within the model boundary. Sliding was assigned for the faults without preferable direction.

Fig. 6
figure 6

Map view of minimum effective stress distribution around Big Lake fault due to the effect of the paleo-stress magnitudes and orientation for a Patchawarra Formation, b Toolachee Formation using FEM. Blue colour in the Big Lake field (arrow) shows the main producing area in the field

Full size image

The Dynel3D results (Fig. 6a, b) show a low minimum horizontal paleo-stress area in the middle of the Big Lake fault. Both the Patchawarra and Toolachee gas reservoirs have this low stress sweet spot although they are hydraulically not connected. The Poly3D model discussed above also predicted current day low stress in the same general area. The publicly available gas production database shows that the best producing well in Big Lake field is in this low stress area, but that same database also shows low rate wells nearby. Our on-going research includes a more detailed study of the correlation between stress and production rate within the study area. More statistically significant results are not yet available.

Dynel3D calculates stress at each time step (during the tectonic history) and retains the highest stress experienced. The highest stresses in this model also occurred along the Big Lake Fault, presumably immediately before fault slip occurred. We compared those maximum paleo-stresses to fractures interpreted in image logs and found a good correlation between maximum paleo-stress and observed fracture orientation and fracture density (Fig. 7).

Fig. 7
figure 7

Predicted fracture network using stress inversion with FEM solver in Dynel3D. Purple colours indicate highly strained fractures which indicate geomechanical sweet spots

Full size image

Traptester (Boundary element method (BEM))

The methodology, advantages, and disadvantages of using BEM as a numerical solver were discussed earlier when Poly3D application was introduced. We used another geomechanical restoration method through a software called Traptester which is a continuum code based on BEM (Sauter and Schwab 2011). The methodology of the code depends on using fault slip and orientation to predict the likely distribution of subsurface strain during past tectonic events, and to predict the intensity and nature of brittle deformation (e.g., Bourne and Willemse 2001; Bourne et al. 2001). It assumes that the main control on fracture generation is the strain perturbation around large-scale faults.

In Traptester, faults are represented as dislocations embedded in an isotropic elastic medium (Elastic Dislocation ED) (Crouch and Starfield 1983). This software determines the control of large faults on the spatial and quantitative distribution of stress and strain within the rock volumes surrounding these faults (Dee et al. 2007). It models the stress and strain changes associated with elastic co-seismic slip on large faults observed on seismic reflection data and neglects the effect of inter-seismic relaxation process. Lateral variation of rock mechanical properties are not taken into consideration when calculating the strain released during dislocation events, as it considers the structural configuration of the major faults as the dominant controller on the strain generation. Also, it uses the elastic rheology for solving the rock behaviour and strain calculation similar to the other methods.

In this study, we used the fault displacements observed on seismic reflection data as the primary input data after running quality control studies on the interpretation to assure accurate results. Faults are then discretised into rectangular panels with horizontal upper and lower edges and uniform slip within every panel. Reduced dimensions of the panels were used with a length of 50 m, for better representing complex fault geometries, then, displacements are calculated at each panel. Elastic strains are then computed at every point in the surrounding horizons by summing the responses to the displacements from every panel of the fault using the ED formulation of Okada (1985, 1992) and using Hooke’s law. The formulation expresses the calculated displacements according to strike, dip, dimensions, and slip vector of the faults and according to Young’s modulus and Poisson’s ratio of the elastic medium which were chosen to be 20,000 MPa and 0.25, respectively. Materials total density was chosen as 2,000 kg/m3, cohesive strength as 20 MPa, and coefficient of internal friction 0.6.

A depth correction of 2,850 m was applied to the calculations to reduce them to the appropriate syn-faulting values as the fault network is now deeply buried compared with when the faults were active. No remote strains were applied to the model as it is going to be assumed without strong base and will affect the results. The effective overburden stress was added to the redistributed stress by incorporating pore pressure of 0.01 MPa/km when calculating the total stress at each point. The computed state of stress at every point is then compared to the standard Mohr–Coulomb failure envelop using 0.75 as the faults coefficient of friction, and 5.5 MPa as the fault cohesive material strength.

Fracturing will occur if the failure envelop is exceeded with a tensile or shear mode depending on which part of the failure envelop is exceeded first by the fault-induced calculated stresses. The angle of the failure planes relative to the principal stress axes was calculated using the standard Coulumb failure criterion (Jaeger and Cook 1979), if shear failure is predicted. If tensile fractures were predicted, they will be oriented perpendicular to the maximum horizontal stress.

We applied the geomechanical restoration technique using Traptester for the Moomba-Big Lake structural model considering forward modelling in a half-space elastic medium (Fig. 8). Several attributes can be calculated on the forward modelled horizons including stress, strain, dislocation, fractures, and deferential stress. As the minimum horizontal stress is used as an indicator on the location of the sweet spots, the same horizons were chosen as observation grids to display the attribute for the purpose of comparison. The same productive area in the Big Lake field showed broad distinctive low stress values indicating highly preferable for hydraulic fracturing. However, the area addressed with the ED method was broader than the previous methods.

Fig. 8
figure 8

Map view of minimum effective stress distribution around Big Lake fault due to the effect of the paleo-stress magnitudes and orientation using BEM. Purple colour in the Big Lake field (arrow) shows the main producing area in the field

Full size image

Comparing shear and tensile fractures predicted in this method with fractures interpreted from image logs showed high correlation in the wells close to Big Lake fault, and low correlation away from the fault.

Summary and conclusions

We have compared several methods for modelling the spatial distribution of stress, strain, and displacement under the effect of present day stress and paleo-stress. Below are listed some major limitations of the models:

  1. 1.

    The geomechanical restoration methods used here assume linear, recoverable stress–strain relations, but laboratory observations show that rocks can have non-linear, non-recoverable behaviour.

  2. 2.

    One of the software packages exhibited an unrealistic sensitivity to changes in the input rock properties. This sensitivity leads us to question the reliability of that one package.

  3. 3.

    All of the software packages require the user to supply rock properties that are rarely known with accuracy.

  4. 4.

    Generation of fractures may be influenced by other factors that are not included in any of these models such as paleo-temperature, bed thickness, inter-seismic relaxation and stress diffusion.

  5. 5.

    Lateral heterogeneity in rock elastic properties has not yet been implemented in any of the software packages we used.

We used the commercial product Poly3D (BEM) to estimate the perturbation of the calculated stresses, strains and displacements (faults and fractures) under the present stress state. Predicted fractures from Poly3D show a uniform conjugate set of vertical fractures oriented 30˚ from the maximum horizontal stress (70° and 130°). Approximately 50 % of the interpreted fractures from image logs match the predicted fracture strike direction, but the fractures seen on image logs are not vertical. Fractures predicted near faults are uniformly perpendicular to the fault plane. This is a user error caused by not assigning cohesion and friction to the faults.

We used Dynel3D (FEM) for geomechanical restoration and estimating stresses and strains exerted during past fault movements. The low stress locations predicted by Dynel3D largely match those low stress locations predicted by Poly3D. Dynel3D also predicted natural fractures and a good correlation was found between those predicted fractures and fractures interpreted on image logs.

Traptester (BEM) also estimates natural fractures generated from past fault movements, but with the elastic dislocation method (ED). Fractures predicted by the ED method showed a good correlation with image logs, but only near major faults. The ED method did not predict fractures away from major faults—but image logs did show fractures away from faults.

All three of the above software packages predicted a significant low stress area adjacent to a bend in the Big Lake Fault. The most productive well in the Big Lake Field is in this low stress area, but so are some average performing wells. We speculate that low stress could lead to higher matrix permeability and/or more successful fracture stimulation treatments. Our ongoing work is focussed on exploring the statistical correlations between gas production rate and the predicted stress and fracture density from the above models.

One of our ongoing questions is: which is more useful for development of a gas field, paleo-stress or present day stress? In our study area, paleo-stress and current day stress are very similar, so it is difficult to say which is more important or useful. However, the fractures predicted by Dynel3D (via structural reconstruction and paleo-stress from FEM) agreed best with the fractures interpreted on image logs.