Introduction

Every year, about 20 to 52 billion tons of sediment are transported by rivers around the world (Khalilivavdareh et al. 2022). The presence of sediment in hydraulic flows causes problems such as reduction of water quality, morphological changes and disruption of hydraulic structures. According to the surveys, there are more than 600 million cubic meters of sediments in the Dez Dam located in Khuzestan province, Iran (Samadiboroojeni et al. 2012). In general, the presence of accumulated sediment in the reservoirs creates problems in two ways: 1- Occupying a useful space by sediment intended for water storage, 2- if these sediments find their way downstream of the dam, it causes damage to water transmission networks and downstream agriculture.

Sedimentation and their distribution in the dam reservoir is one of the most important factors in determining the useful life of a reservoir. It is also known that the useful life of a reservoir has a direct relationship with the efficiency of the dam. According to the mentioned issues, it can be concluded that the sedimentation is one of the important and influential factors on the economic aspect of the dam (Lisle et al. 2001). Annually, on average, 0.5 to 1% of the storage volume of dams is occupied by sediments. This number is more than 4% for many dams. As a result, most dams lose their efficiency and full capacity within 25 to 30 years (Verstraeten et al. 2003). According to the mentioned points, it is clear that the phenomenon of sedimentation is one of the important factors threatening big investments in water projects.

The river bed layer is a thin layer of the water flow, which is usually up to 2 times the size of the sediment particles and is located immediately after the river bed. The sediments in the river flow are divided into three categories: wash load, suspended load and bed load (Sadeghi et al. 2018; Awal et al. 2019). A major part of the total sediment load in rivers is the suspended sediment load (Khosravi et al. 2022). Suspended sediment load refers to materials that are carried above the bed layer by water and remain suspended in water for a long time (Parsons et al. 2015).

It is clear that the issue of suspended sediment load is of great importance (Essam et al. 2022). One of the preventive solutions to deal with the problems caused by suspended sediment load is its simulation and estimation. One of the most basic methods presented to estimate the suspended sediment load is called sediment rating curve. In this method, the relationship between the suspended sediment load and its corresponding river flow rate is obtained through curve fitting of these two parameters. Due to the fact that many factors and parameters are involved in the phenomenon of sediment transport, its simulation process is complicated and linear relationships are not able to describe this phenomenon well. Therefore, the sediment rating curve method has low accuracy and this has been proven in most cases (Pronoos Sedighi et al. 2023).

In recent years, many methods have been presented to simulate and estimate the suspended sediment load, which are more accurate than the sediment rating curve method. Aytek and Kişi, (2008) by simulating the phenomenon of sedimentation in Tongue River located in the state of Montana, USA, using the genetic programming method and comparing it with the sediment rating curve and regression methods, concluded that the genetic programming method is more accurate than the sediment rating curve method. Kisi and Shiri (2012) investigated three simulation methods including artificial neural network, gene expression programming, and adaptive neuro-fuzzy inference system using measured data of suspended sediment load belonging to the Eel River located in the United States. The results indicated that the gene expression programming method has a better performance than the other methods.

Salih et al. (2020) investigated and compared several machine learning methods, including the feature selection classification method, M5P, K-Star and M5Rules models, in order to simulate the suspended sediment load of the Delaware River located in the United States. They found that among the applied data mining models, the M5P model is more accurate in simulating suspended sediment load. AlDahoul et al. (2021) simulated the suspended sediment load of Johor River in Malaysia by using the methods of Multi-layer perceptron (MLP) neural network, Extreme gradient boosting, Long short-term memory (LSTM) and Elastic Net linear regression with four time series scenarios. Finally, after comparing the results, it was found that the Long short-term memory method is more accurate than other used methods.

One of the latest methods presented in the simulation of suspended sediment load is the use of artificial intelligence or machine learning. In machine learning, the development of intelligent systems that perform the learning process by analyzing past experiences is discussed. Among the many machine learning algorithms, Support Vector Machine (SVM) can be mentioned. The support vector machine was first proposed by Vapnik (Vapnik and Lerner 1963; Vapnik and Chervonenkis 1964). This method achieves a general optimal solution using the principle of Structural Risk Minimization (SRM). Support vector machine is generally used for classification and classification problems, but Drucker et al. (1996) updated the support vector machine and presented a new method called support vector regression, which can be used in simulation problems. In the past few years, many researchers have used support vector regression to simulate and estimate suspended sediment load, and the results of most of them indicate the high accuracy and efficiency of this method in modeling suspended sediment load.

Lafdani et al. (2013) investigated and compared the ability of support vector machine and artificial neural network in predicting suspended sediment load. This was done by using the measured data of the Doiraj River located in Ilam province, west of Iran, and using the river flow rate and rainfall values as input to the model. They indicated that both models have sufficient accuracy, but the nu-SVR model with RBF kernel has higher accuracy than other kernels. Hazarika et al. (2020a) used two methods of artificial neural network and support vector regression to simulate and estimate the suspended sediment load of the Tawang Chu River in India. Finally, using the obtained results, it was determined that the support vector regression method had a lower error and was considered as the best model. Hazarika et al. (2020b) by combining the wavelet transform model with two extreme learning machines models and twin support vector regression and simulating the suspended sediment load, concluded that the combined models with the wavelet transform model have higher accuracy and also the application of the support vector machine and support vector regression models were proved in general. Doroudi et al. (2021) presented new combined methods for simulating suspended sediment load by combining SVR model with optimization methods such as observed-teacher-learner-based optimization method and genetic algorithm. The studied models were evaluated using statistical indices, and the combined SVR-OTLBO model was recognized as the best model. Also, the accuracy of the SVR model was generally confirmed. Noori et al. (2022) investigated two general methods of multiple linear regression and support vector regression to simulate the total sediment load in rivers. By examining the results, it was found that the support vector regression method based on the radial basis function kernel performed well in predicting the total sediment load. Kumar et al. (2022) evaluated five simulation models including artificial neural network, wavelet-based artificial neural network, support vector machine, wavelet-based support vector machine and multiple linear regression. By examining the results, it was found that the wavelet-based support vector machine method is more accurate than other methods. Shakya et al. (2023) tried to investigate the effectiveness of machine learning models in predicting suspended sediment load. They came to the conclusion that machine learning methods, including support vector regression, work very well in predicting suspended sediment load and are more efficient than other existing methods.

Salarijazi et al. (2024) conducted a study in which they estimated the suspended sediment load using a developed model of the sediment rating curve and data recorded from ten hydrometric stations in Ghareh-Sou coastal watershed, located in the north of Iran. The researchers found that classifying the data based on the average relative to the median resulted in a more accurate estimation of the suspended sediment load.

In this study, two important issues of artificial intelligence and the phenomenon of sediment transport have been addressed. In general, the use of artificial intelligence and machine learning methods is a new way of simulating and predicting hydraulic parameters. Regarding the estimation of the suspended sediment load corresponding to the river flow rate, a model should be used that covers the extreme values well (Khalili et al. 2016; Khozeymehnezhad and Nazeri Tahroudi 2019; Nazeri Tahroudi et al. 2019; Ahmadi et al. 2022).

In this research, the support vector regression method is used, which is a machine learning method. The main goal of this study is to predict the suspended sediment load of the Zohreh River, Iran using the support vector regression. According to the investigations carried out on the previous researches, it was concluded that in the topic of suspended sediment load prediction, the combination of nonlinear support vector regression model with different optimization algorithms from the type of crowd intelligence has not been discussed. Like many other machine learning methods, support vector regression also includes two steps of train and test in simulation. In this study, optimization algorithms from the type of crowd intelligence were used to train the support vector regression model. In this research, the ant colony, the ant lion, the dragonfly and the salp swarm optimization algorithms have been used to perform the train phase of the nonlinear support vector regression. In this study, the accuracy and efficiency of the nonlinear support vector regression model were increased by using new algorithms to optimize the parameters. In fact, an optimized hybrid model is proposed in this study to simulate the suspended sediment load.

Materials and methods

Study area and used data

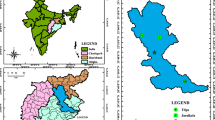
With an approximate length of 490 km, the Zohreh River is one of the longest rivers in Iran and plays a significant role in water supply in the fields of drinking, industry and agriculture (Fig. 1). The basin area of this river includes an area equal to 16,033 square kilometers, of which 10,789 square kilometers belong to mountainous areas and the other 5244 square kilometers include plain lands. In this research, the measured data of river flow rate and suspended sediment load measured at the Deh Molla hydrometric station located in Khuzestan province at the 30.30 degrees north and 40.49 degrees east were used and include the number of 578 events of suspended sediment load in the period of 1983–2018, which can be shown in Fig. 2. The maximum and minimum river flow rate are 1139 and 1.2 m3/s, respectively, and the suspended sediment load values vary from 1.8 to 1,278,013 tons per day (Table 1).

Fig. 1
figure 1

The route of the Zohreh River and the location of Deh Molla station

Full size image
Fig. 2
figure 2

Measured values of river flow rate (m3/s) and suspended sediment load (ton/day)

Full size image
Table 1 Minimum, maximum, mean values and standard deviation of the measured data
Full size table

Support vector regression

Support vector regression is one of two types of support vector machine, which is a method for data classification, and the second type, which is called support vector regression, is inspired by the topic of data classification and performs simulation. In general, SVR is a more advanced version of SVM that is used for modeling (Smola and Schölkopf 2004). Support vector regression can be of both linear and nonlinear forms. The nonlinear mode of support vector regression with RBF kernel function was utilized in this study. Three parameters-ɛ, C, and Sigma—were sought to be optimized in the study. The general approach of the support vector regression method involves first generating a series of answers and then defining a penalty value (LP) based on the acceptable error value for data outside the desired range. This value should be minimized to achieve the best answer (Basak et al. 2007). Due to the complexity of the nonlinear form, first the problem is assumed to be linear and finally it is solved in a nonlinear form using kernel functions (Awad and Khanna, 2015). The general form of a linear regression is y = wTxi + b. Now, in order to obtain the values of w and b, the general process is as follows:

First, by solving Eq. (1), the values of a+ and a− are obtained.

$$\min \frac{1}{2}\mathop \sum \limits_{i} \mathop \sum \limits_{j} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)\left( {a_{j}^{ + } - a_{j}^{ - } } \right)x_{i} Tx_{j} - \mathop \sum \limits_{i} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)t_{i} + \varepsilon \mathop \sum \limits_{i} \left( {a_{i}^{ + } + a_{i}^{ - } } \right)$$
(1)

Then, the set s is determined:

$$s = \left\{ {i|0 < a_{i}^{ + } a_{i}^{ - } < c} \right\}$$
(2)

Now, the value of w is calculated according to the set of s.

$$w = \mathop \sum \limits_{i} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)x_{i}$$
(3)

Then, the value of b is extracted from Eq. (4) by knowing the value of s and w.

$$b = \frac{1}{s}\mathop \sum \limits_{i \in s} \left[ {t_{i} - wTx_{i} - {\text{Sign}}\left( {a_{i}^{ + } - a_{i}^{ - } } \right)\varepsilon } \right]$$
(4)

Now, to change the form from linear regression to nonlinear, kernel functions are used and the relationships are changed in the form of Eq. (5).

$$\min \frac{1}{2}\mathop \sum \limits_{i} \mathop \sum \limits_{j} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)\left( {a_{j}^{ + } - a_{j}^{ - } } \right)K\left( {x_{i} x_{j} } \right) - \mathop \sum \limits_{i} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)t_{i} + \varepsilon \mathop \sum \limits_{i} \left( {a_{i}^{ + } + a_{i}^{ - } } \right)$$
(5)
$${\text{s.t}}\left\{ {\begin{array}{*{20}c} {\mathop \sum \limits_{i} \left( {a_{i}^{ + } - a_{i}^{ - } } \right) = 0} \\ {0 \le a_{i}^{ + } \le c , 0 \le a_{i}^{ - } \le c} \\ \end{array} } \right.$$
(6)

In this case, the model is written as Eq. (8).

$$W = \mathop \sum \limits_{i} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)x_{I}$$
(7)
$$y = \mathop \sum \limits_{i} (a_{i}^{ + } - a_{i}^{ - } )K\left( {x_{i} ,x} \right) + b$$
(8)

As a result, the value of b is equal to:

$$b = \frac{1}{s}\mathop \sum \limits_{i \in s} \left[ {t_{i} - \mathop \sum \limits_{i \in s} \left( {a_{i}^{ + } - a_{i}^{ - } } \right)K\left( {x_{I} ,x} \right) - \varepsilon {\text{Sign}}\left( {a_{i}^{ + } - a_{i}^{ - } } \right)} \right]$$
(9)

Equations change depending on the type of used kernel function. It should be noted that in order to find the optimal line for the data, quadratic programming methods (QP), which are well-known methods for solving constrained problems, are used. The Karush–Kuhn–Tucker condition is considered to obtain the support vector values. The Karush–Kuhn–Tucker or Kuhn-Tucker conditions are necessary conditions for the optimal solution in nonlinear programming. Kahn–Tucker is actually a generalization of the method of Lagrange coefficients, which also considers inequality constraints. The range of changes in support vector regression parameters was selected according to various studies in this field (Nazeri Tahroudi et al. 2018; Nazeri Tahroudi and Ramezani 2020; Eslami et al. 2022).

Ant colony optimization algorithm

The ant colony algorithm was first introduced by Dorigo (1992). This algorithm is inspired by the behavior of ant swarm in routing and performs optimization. Ants leave a chemical substance called pheromone along the path they travel, which disappears over time. Pheromone is the basis of path selection for other ants. So, ants always choose a path that has more remaining pheromone. Repetition of this process makes the paths chosen by the ants to be optimized and the shortest path to the goal is determined (Dorigo 1992). This algorithm is included in the category of computational intelligence and crowd intelligence methods. Swarm intelligence is a type of intelligence that is created from the crowd of a series of agents and none of its members are individually intelligent.

The algorithm presented in 1992 was used for discrete problems, but Socha and Dorigo, (2008) presented a more advanced version of this algorithm, inspired by its initial state, to solve continuous problems. The difference between these two models was that in the ACO algorithm, instead of choosing a series of discrete points, a Gaussian kernel function is used. Also, this algorithm has the ability to tolerate correlation in variables. The working process of this algorithm is that first, a series of solutions is created randomly using the specified intervals for the parameters, and their cost function is calculated and they are sorted from the best to the worst solution. The created answers are stored in an environment called archive.

Now, a Gaussian distribution is considered for each of the answers in the archive. The standard deviation of the Gaussian distribution for each answer depends on the distance of the considered answer with other answers. The WL and PL components are calculated.

$$W_{L} = \frac{1}{{qK\sqrt {2\pi } }}{\text{exp}}\left( { - \frac{1}{2}\left( {\frac{L - 1}{{qK}}} \right)^{2} } \right)$$
(10)

, where q is the selection pressure and k is the number of ants. The value of L is always equal to one or more than one.

$$P_{L} = \frac{{W_{L} }}{{\mathop \sum \nolimits_{m} w_{m} }}$$
(11)

PL is the probability of selecting the component from the considered Gaussian to produce a new solution. Then, with Gaussian distributions and the probability of their selection, a certain number of new random samples are created and transferred to the archive, and their cost function is calculated and sorted. Finally, additional members are removed from the archive and a new archive is created. This process continues until the termination conditions are met to determine the optimal solution (Duan and Yong 2016).

Ant lion optimization algorithm

The ant lion optimization algorithm is a swarm intelligence algorithm that was introduced in 2015 inspired by the behavior of ant lions in hunting ants (Mirjalili 2015). This algorithm has no adjustment parameters and has relatively few steps, so the optimization speed in this algorithm is high and it does not stop at local optimal points and finds the overall optimal point. The hunting process of the ant lion is that first, the ants move randomly in the search space, and after entering the cone-shaped trap, the ant lion makes the trap smaller by throwing sand on top of the trap so that the ant cannot escape. Finally, when the ant reaches the center of the ant trap, it is hunted by the ant lion. All these steps in the algorithm are expressed as mathematical relationships (Scharf and Ovadia 2006).

The steps of the algorithm are described as follows: first, according to the upper and lower limits of the variables, the number of n ants and ant lion is produced, and their fit value is calculated by the cost function, and in the matrices Mant (the matrix of the ants' position), Moa (the fitness matrix of the ants), Mantlion (ant lion position matrix) and Moal (ant lion fitness matrix) are stored. Now, the main cycle of the algorithm starts. At the beginning of each iteration, the values of I, ct and dt are updated using Eqs. 12, 13, and 14.

$$c^{t} = \frac{ct}{I}$$
(12)
$$d^{t} = \frac{dt}{I}$$
(13)
$$I = 10^{W} \frac{t}{T}$$
(14)

, where ct is the lower bound in the current iteration, dt is the upper bound in the current iteration, and ct and dt are the lower and upper bounds in the previous iteration, respectively. The value of w is set according to the current iteration number. Also, t and T are the current iteration number and the total number of iterations. The following steps are performed for each ant: First, an ant lion is selected using the roulette wheel, and \(c_{i}^{t}\) , and \(d_{i}^{t}\) values are calculated using its position.

$$d_{i}^{t} = {\text{antlion}}_{j}^{t} + d^{t}$$
(15)
$$c_{i}^{t} = {\text{antlion}}_{j}^{t} + c^{t}$$
(16)

Then, according to the values of \(c_{i}^{t}\) and \(d_{i}^{t}\), a random movement around the selected ant lion is made and it is calculated in the form of Eq. (17).

$$x_{i}^{t} = \frac{{\left( {x_{i}^{t} - a_{i} } \right)\left( {d_{i} - c_{i}^{t} } \right)}}{{(d_{i}^{t} - a_{i} )}} + c_{i}$$
(17)

The current random movement around the best ant lion is also calculated and the new position of the ant is calculated from Eq. (18).

$$ant_{i}^{t} = \frac{{R_{A}^{t} + R_{E}^{t} }}{2}$$
(18)

, where \(R_{A}^{t}\) is the random walk around the ant lion selected by roulette wheel and \(R_{E}^{t}\) is the random walk around the best ant lion. Finally, if the objective function calculated for the new ant is better than the objective function of the corresponding ant lion, the location of the ant lion becomes equal to the location of the new ant.

Dragonfly optimization algorithm

Dragonfly optimization algorithm was introduced for the first time in 2016 (Mirjalili 2016). This algorithm performs optimization by being inspired by the unique crowding behavior of dragonflies in hunting and migration (Mirjalili 2016). Dragonflies form small groups to hunt and search and explore and move back and forth in a small area to catch other insects. This mass formed by dragonflies is called static mass, which is similar to the exploitation phase in optimization algorithms.

Also, these insects fly in one direction and a long distance to migrate in a large mass, which is called a dynamic mass and is similar to the exploration phase in optimizer algorithms (Russell et al. 1998; Wikelski et al. 2006). To simulate the movement of insects, Reynolds (1987) has shown three basic principles including separation, alignment and cohesion, which are calculated as the following equations. Also, attracting dragonflies to the food source and repelling them from the enemy is called cohesion and distraction, and they are defined using the following relationships.

$$S_{i} = - \mathop \sum \limits_{j = 1}^{N} X - X_{j}$$
(19)
$$A_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} V_{j} }}{N}$$
(20)
$$C_{i} = \frac{{\mathop \sum \nolimits_{j = 1}^{N} X_{j} }}{N} - X$$
(21)
$$F_{i} = X^{ + } - X$$
(22)
$$E_{i} = X^{ - } + X$$
(23)

, where Si, Ai, Ci, Fi and Ei are the separation, alignment, cohesion, absorption and distraction factors, respectively. X is the position of the current person, N is the number of neighbors of the current person, Xj is the position of the Jth person, Vj is the speed of the Jth person, and X+ and X− are the positions of the food source and the enemy, respectively. These three factors are used to simulate the movement of dragonflies. The position of the dragonfly is updated using two vectors: length step (∆x) and position (x). The values of these two vectors are calculated using Eqs. (24) and (25).

$$\Delta x_{t + 1} = \left( {sS_{i} + aA_{i} + cC_{i} + fF_{i} + eE_{i} } \right) + W\Delta x_{t}$$
(24)
$$x_{t + 1} = x_{t} + \Delta x_{t + 1}$$
(25)

, where s, a, c, f and e are the coefficients of separation, direction, cohesion, absorption and distraction, respectively, and t is the iteration counter. Neighborhood is an important issue in the dragonfly algorithm, so a neighborhood radius is considered and it is checked, whether there is another dragonfly in this range or not. If there is another dragonfly within the neighborhood radius, it is considered as a neighbor and the five mentioned factors are calculated according to the neighbors, and if there is no neighbor, the position of the dragonfly is calculated using random walk. The general process of the dragonfly algorithm is that first, it is valued according to the upper and lower bounds of the position of the dragonflies, and then the length of the first steps is also randomly valued. The value of the cost function is calculated and the best and worst members are identified, and the values of W, s, a, c, f and e are calculated for each member of the community. Now, a neighborhood radius is considered, and the neighbors of each member are determined, and the values of S, A, and C are calculated accordingly. In the next step, the value of E and F is calculated according to the food source and the enemy located in the neighborhood. It is also worth mentioning that if there is no food source and enemy in the neighborhood of the member in question, their value is considered equal to zero, but if there is no other member in the neighborhood of the member in question, the movement of dragonflies is random. Finally, after updating the dragonfly's position, the value of the cost function is calculated and if its value is better than the current food source, it is placed as a food source. This process continues until the termination conditions are met.

Salp swarm optimization algorithm

The salp swarm algorithm (SSA) was introduced in 2017, inspired by the swarming behavior of salps (Mirjalili et al. 2017). Salps are organisms with transparent bodies that are able to move by pumping water from their bodies (Madin 1990). The swarming behavior of salps is such that a chain is formed and one salp at the beginning of the chain assumes the leadership role and the rest of the salps follow it.

So, the collective behavior of salps was in the form of a chain that originated by using rapid and coordinated changes of salps to chase food (Anderson and Bone 1980). In this algorithm, the position of each salp has N dimensions, where N represents the number of variables in the problem; Therefore, the position of salps is stored in a two-dimensional matrix named x and a food source named F' is considered as the target of collection. Therefore, Eq. 26 is used to update the position of the chain leader.

$$x_{J}^{I} = \left\{ {\begin{array}{*{20}c} {F_{J}{\prime} + C_{1} \left( {\left( {ub_{j} - lb_{j} } \right)*c_{2} + lb_{j} } \right) , c_{3} \ge 0} \\ {F_{J}{\prime} - C_{1} \left( {\left( {ub_{j} - lb_{j} } \right)*c_{2} + lb_{j} } \right) , c_{3} \ge 0} \\ \end{array} } \right.$$
(26)

, where \({\text{x}}_{{\text{J}}}^{{\text{I}}}\) is the position of the salp of the leader in iteration J and dimension I, and \(F_{J}{\prime}\) is the position of the food source and C2 and C3 are random numbers between zero and one. The coefficient C1 is the most important parameter in the SSA because it balances exploration and exploitation in each iteration and is calculated by Eq. 27:

$$C_{1} = 2*e^{{\left( {\frac{ - 4*I}{L}} \right)^{2} }}$$
(27)

I is the current iteration number and L is the total number of iterations. Now, Newton’s law of motion is used to update the position of follower salps, which is in the form of Eq. 28:

$$x_{j}^{i} = \frac{1}{2}a + t^{2} + v_{0} t$$
(28)

, where \(x_{j}^{i}\) indicates the position of salp i in dimension j and v0 and a are equal to the initial velocity and acceleration, respectively. Considering that in optimization problems, time is the same as iteration and that the difference between each iteration is equal to one, and also considering that the initial speed is zero, the above equation is changed to Eq. (29):

$$x_{j}^{i} = \frac{1}{2}\left( {x_{j}^{i} + x_{j}^{i - 1} } \right)$$
(29)

Evaluation criteria

In this research, the performance of support vector regression model and optimization algorithms were evaluated by three statistics: RMSE, NSE, and R2. The equations for calculating the discussed statistics are shown in Eqs. 30, 31 and 32, where \(X_{o}\) is equal to the observed values, \(X_{s}\) is the simulated values, \(\overline{X}_{O}\) is the average of the observed values, \(\overline{X}_{s}\) is the average of the simulated values and N is the number of data.

$${\text{RMSE}} = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {X_{o} - X_{s} } \right)^{2} }}{N}}$$
(30)
$${\text{NSE}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{N} \left( {X_{o} - X_{s} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{N} \left( {X_{o} - \overline{X}_{O} } \right)^{2} }}$$
(31)
$$R^{2} = \left( {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{s} - \overline{X}_{s} } \right)\left( {X_{o} - \overline{X}_{O} } \right)}}{{\sqrt {\mathop \sum \nolimits_{i = 1}^{n} \left( {X_{s} - \overline{X}_{s} } \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {X_{0} - \overline{X}_{0} } \right)^{2} } }}} \right)^{2}$$
(32)

Information of used computer

Considering that the execution speed of the algorithms has a direct relationship with the processing power of the computer’s system, therefore, the information of the used system in this research to execute the algorithms are as follows. Intel Core i7-4700HQ 2.4 GHz processor, 8 GB DDR3 RAM and internal SSD hard drive.

Results and discussion

In the present research, the trend of changes in the studied data was initially examined using the modified Mann–Kendall test. Based on the results of this test, it was determined that a significant trend is not present in the studied data. A total of 578 suspended sediment load events from Deh Molla station between 1983 and 2018 were investigated in this study. The utilized model in this research is the optimized support vector regression, which belongs to a nonlinear regression type and encompasses three parameters: C, ε, and Sigma. These parameters are crucial for model and their correct values greatly enhance simulation precision. Optimization algorithms were employed to estimate these three parameters effectively. Four crowd intelligence algorithms including ant colony optimizer (ACO), ant lion optimizer (ALO), dragonfly algorithm (DA), and salp swarm algorithm (SSA) were utilized for this purpose.

In all four aforementioned algorithms, two influencing factors on the final solution are considered: number of iterations and population. In order to determine their impact on the final answer, these factors were set at low values and gradually increased through four steps. In step one, 25 iterations and a population size of five were used. Subsequently, in step two, iterations were increased to 50, while maintaining other settings constant. Moving on to steps three and four, respectively involved considering 100 iterations a population size of ten followed by adopting 200 iterations with a population size of 20. It was found through investigations that the results are not improved by increasing the number of iterations to more than 200. It has been demonstrated by several studies that when an optimization approach is utilized to optimize model parameters of SVR, the error is reduced and the number of iterations required to achieve optimal performance is minimized (Raji et al. 2022; Eslami et al. 2022).

It should be noted that 80% of the data were used to train phase and the remaining 20% of the data were used to test phase. The combination of two support vector regression and optimization algorithms resulted in an increase in calculations, leading to a relatively longer run time. As a result, the run time for running the algorithms was recorded in different iterations, so that at the end, the time factor can be utilized as a feature in decision making and selection of the best algorithm. It should be noted that the range of changes for the three desired parameters was determined based on various studies, which are shown in Table 2.

Table 2 Range of changes of the support vector regression parameters
Full size table

The train phase of the SVR model was conducted using 80% of the data, with the objective function being the RMSE in the optimization algorithms shown. Table 3 presents the results of the train phase of the SVR model using optimization algorithms in four iterations. Additionally, Table 4 provides details on the calculated criteria for each optimization algorithm in these iterations during the train phase. As seen on Table 4 and scatter plots shown in Figs. 3, 4, 5, and 6, it is evident that at low iterations (25 and 50), ant colony, ant lion, and dragonfly algorithms did not yield satisfactory simulations as indicated by high calculated errors.

Table 3 Optimized values of the support vector regression parameters
Full size table
Table 4 Calculated criteria in the train phase of the support vector regression model
Full size table
Fig. 3
figure 3

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 25 iterations in the train phase

Full size image
Fig. 4
figure 4

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 50 iterations in the train phase

Full size image
Fig. 5
figure 5

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 100 iterations in the train phase

Full size image
Fig. 6
figure 6

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 200 iterations in the train phase

Full size image

However, with an increase in iterations, error values significantly decreased resulting in more accurate simulation outcomes. Notably, unlike other three algorithms, dragonfly algorithm lacked sufficient accuracy at a higher iteration (100). Moreover, the results indicate that SSA produced sufficiently accurate results within 25 iterations. In terms of run time during model train phase, the SSA required slightly more time compared to ACO, while DA was slower than both SSA and ALO at equal iteration. Therefore, in terms of run time, ACO and SSA ranked first and second, respectively, while ALO and DA ranked third and fourth, respectively. Additionally, it is worth mentioning that an increase in population size influenced run time duration across discussed algorithms.

Upon completion of the model train phase, the remaining 20% of the data was utilized for testing the simulation of suspended sediment load. The model inputs comprised river flow rate values, while the measured suspended sediment load values at Deh Molla station were used as target values. Modeling was conducted using optimized support vector regression model parameters through optimization algorithms in 25, 50, 100 and 200 iterations. The results demonstrating prediction of suspended sediment load values at Deh Molla station are shown in scatter plots in Figs. 7, 8, 9 and 10 and shown quantitatively in Table 5.

Fig. 7
figure 7

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 25 iterations in the test phase

Full size image
Fig. 8
figure 8

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 50 iterations in the test phase

Full size image
Fig. 9
figure 9

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 100 iterations in the test phase

Full size image
Fig. 10
figure 10

Scatter plot of simulated data using the support vector regression model optimized by optimization algorithms with 200 iterations in the test phase

Full size image
Table 5 Calculated criteria in the test phase using the support vector regression model optimized by the optimization algorithms with different iterations
Full size table

The results from Table 5 and scatter plots in Figs. 7, 8, 9 and 10 reveal that within 25 iterations, all algorithms except SSA demonstrate low accuracy with simulated values generally lower than their measured values. In contrast, in 50 iterations, ACO and SSA produced acceptable error values and successful simulations. However, the simulation performed by the other two algorithms, namely ALO and DA, was not satisfactory, and the values produced by these models differed significantly from the measured values. In 100 iterations, good results were achieved by three algorithms, namely ACO, ALO, and SSA, while only DA did not perform well. In 200 iterations, all models demonstrated satisfactory performance with error values close to zero.

The optimization process was effectively carried out in the ACO, resulting in simulation results demonstrating satisfactory accuracy when using the parameters optimized by this algorithm in the test phase. However, it is important to note that in low iterations, specifically 25 iterations, this algorithm did not perform the optimization process well. Consequently, the RMSE was very high and other evaluation criteria indicated a low level of accuracy in optimization and simulation. The results obtained indicate that as iteration and population numbers increase, the final solution tends to become more optimal. In terms of run time values, it is evident that as the number of iterations and population increases, this algorithm requires more run time for optimization. Therefore, it can be concluded that allocating more run time to optimizing the model would yield a more optimal solution. Similar conditions apply to ALO as with ACO; an increase in iteration and population numbers leads to a tendency for the final solution to become more optimal. According to calculated criteria, it can be observed that optimization and simulation were not successful during 25 and 50 iterations with significantly high RMSE values. It should be noted though that unlike ACO, where only 25 iterations exhibit high error values, while others are acceptable; all iterations show increased run times compared to ACO. Based on these observations, it can be concluded that ACO performs better than ALO. The trend of improving results with increasing iteration number and population size holds true for DA as well. However, similar to ALO but unlike ACO, the desired results were only obtained after 200 iterations with unsatisfactory outcomes during 25, 50, and 100 iterations. The presented results clearly indicate lower accuracy for DA compared to the previous two algorithms. Additionally, the run time per each iteration is equal to 18.1, 19, 48, and 137.3 s, respectively. In equal conditions, the DA requires more run time. On average, the optimization process took 7 h and 36 min with 200 iterations. Based on these given circumstances, it can be concluded that DA performs weaker in comparison with the two algorithms of ACO and ALO.

The SSA generally demonstrates similar behavior to the other discussed algorithms, with the error decreasing and run time increasing as a result of increasing the number of iterations and population in this algorithm. However, the main difference between this algorithm and the others is that favorable results were achieved with 25 iterations. The obtained results indicate good accuracy of the model at a low number of iterations. In different iterations, all R2 coefficients are equal to 1 and NSE is equal to one, except for 25 iterations, where it is equal to 0.99. Comparatively, these overall outcomes align with prior research such as Hazarika et al. (2020b), supporting vector regression as a suitable method for predicting suspended sediment load with minimal error. The results are consistent with the research conducted by Hazarika et al. (2020a) indicating that the combined support vector regression method demonstrates high accuracy in simulating suspended sediment load. Similarly, agreement was found between the results of this research and those of Doroudi et al. (2021), both highlighting the high efficiency and accuracy of the support vector regression model. Furthermore, it was determined that the obtained results align well with those of Kumar et al. (2022), reaffirming the proven high efficiency of the SVR model. Asadi et al. (2021) also confirmed the effectiveness of support vector machine in simulating suspended sediment load.

Figure 11 shows the violin plot of the measured and simulated suspended sediment load using the support vector regression model, which was optimized by optimization algorithms in 200 iterations. It can be shown from Fig. 11 that the certainty of the studied algorithms is similar and high. Additionally, it can be seen that the average, first and third quartiles, as well as the range of changes of the measured and simulated values are very similar, indicating good performance of the optimization algorithms in optimizing the parameters of the support vector regression model in nonlinear mode.

Fig. 11
figure 11

Violin plot of measured and simulated suspended sediment load using the support vector regression model optimized by optimization algorithms with 200 iterations

Full size image

Conclusion

Upon examination of all the obtained results, it was determined that, overall, the support vector regression model is a suitable method for predicting suspended sediment load, and when the parameters of this model are well adjusted, highly accurate results are obtained from it. It was determined that the SSA yielded superior results compared to the other algorithms under consideration, making it the preferred method for adjusting and optimizing the parameters of the support vector regression model. The optimization of the salp swarm algorithm was successfully performed with a low number of iterations and shorter run time compared to other models. By conducting 25 iterations and consuming minimal run time, a remarkably low and acceptable error was achieved using this algorithm. It is important to note that the determination of the number of iterations should also take into account the evaluation criteria. Furthermore, based on the research findings, it is evident that a reliable prediction of the suspended sediment load can be achieved by utilizing the two parameters of river flow rate and its corresponding suspended sediment load. It was found in this study that the approach utilized outperformed the conventional SVR method and other regression-based approaches by optimizing model parameters, resulting in improved performance. Furthermore, it was observed that the integration of optimization algorithms with the SVR model not only enhanced simulation performance but also significantly reduced the number of iterations needed to achieve an optimal state. Considering optimizing the parameters of the support vector regression model using different algorithms, the proposed model has no spatial limitations.