Introduction

Rapid population growth, urbanization, unreliable and costly treatment options, and poor water quality are all contributing factors to the growing worldwide concern about water pollution (Rajkumar and Palanivelu 2004; Bhagawan et al. 2018). Industries, such as distilleries, wet coffee processing, oil mills, textile productions, processing of food and chemical, soft drinks, papers, and metals production, were producing a large amount of wastewater (Gebeyehu et al. 2018). Waste containing different pollutant is becoming a major environmental threat as a result of the fast expansion of industries like wet coffee processing industries and other pesticide industries in Ethiopia (Mosivand et al. 2018). Chemical compounds are produced and used on a far larger scale now than ever before, which implies that many of them end up in the environment and are not biodegradable. Industries generate a lot of pollutants, such as bio-refractory organic compounds, which have negative effects on the aquatic ecosystem and environment due to their toxicity, color, and odor. An increasing volume of organic/inorganic wastewater from different industries deals about different business, but on the other hand, there are strict legal restrictions on how to dispose of wastewater (Vinicius et al. 2022).

Seven million tons of coffee are consumed worldwide each year, making it one of the most popular drinks in the world (Villanueva-Rodríguez et al. 2014). For nations that produce coffee, it is a significant agricultural crop. The estimated 5.5 million tons of coffee produced annually worldwide, or 6.4%, come from Ethiopia. 55.35% of the nation’s annual total output is produced in the west, south, and east, respectively. The agricultural land in the nation has roughly 600,000 hectares of coffee plantations. One of the most important issues confronting developing nations is the improper management of enormous volumes of waste produced by various human activities. Even more challenging is the risky dumping of these harmful chemicals and contaminates such as high organic concentrations, nutrients, suspended matter, and highly acidic wastewater into the environment (Ali et al. 2021; Mohyudin et al. 2022; Rasheed et al. 2022). In particular, freshwater reservoirs are quite susceptible. In Africa, social and economic underdevelopment usually contributes to organic contamination of inland water systems. One of the most environmentally destructive agro-based industries is the coffee processing industry. The disposal of effluent from pulping, fermenting, and washing coffee beans poses a variety of problems for the receiving environment, especially aquatic bodies, in many coffee processing nations. Wet processing is considered to produce coffee of a better quality than dry processing. Currently, Ethiopia has more than 400 wet coffee processing facilities, many of which are situated close to rivers (Woldesenbet et al. 2014).

A significant amount of organic compounds that might harm the environment are present in coffee wastewater. During the wet coffee processing process, the pulp and mucilage of coffee cherries are eliminated. Coffee effluent contains a lot of organic chemicals, which might harm the environment. Wet coffee processing wastewater is made up of caffeine-rich coffee fruits, sugars, phenolic compounds, fatty acids, lignin, cellulose, pectic chemicals, and other macromolecules that are undesirable for disposal in soil and water bodies (Sahana et al. 2018). Excess phosphate and nitrate concentrations in coffee wastewater effluents directed to the environment create eutrophication, which is one of the most common problems in the monitoring of environmental water sources today (Chen et al. 2014). A significant amount of acidic waste is created as a result of the high proportion of organic materials used in this process, which is especially hazardous to the environment.

As a consequence, prior to discharge into water bodies, treatment is necessary (Tacias-Pascacio et al. 2018). The physiochemical process is not economical, necessitates excessive chemical usage, and simultaneously produces a sizable volume of sludge. The biological treatment approach, which is a long and drawn-out process, requires high dilution (Shahedi et al. 2020). Finding a method to manage industrial waste that is affordable is crucial.

The process of electrochemistry has received a great deal of attention for the treatment of different forms of industrial waste, such as wet coffee processing, paper, distiller organic fertilizer, automotive industry, potentially toxic metals and tanner metal, metal plating wastewater, and real industrial waste by using pulsed electrochemical process (PECP) (Vasudevan 2012; Mahesh et al. 2016; Payami Shabestar et al. 2021). Electrochemical treatment, or electro-oxidation, has been proposed as a viable option for a variety of industrial effluents (AlJaberi 2019; AlJaberi et al. 2020). The treatment of pesticide processing industrial waste was carried out in the current study by utilizing an electrochemical method as well as a combination of other advanced technologies (Science 2018; Mena et al. 2019; Akter and Islam 2022).

The utilization of electrochemical treatment methods for the removal of organic and inorganic components from wastewater is a promising approach, due to its affordability and user-friendly technology (Bernal-Martínez et al. 2013; Sahana et al. 2018; AlJaberi et al. 2020; Ebba et al. 2022). Pulsed electrochemical wastewater treatment method is one of the most widely used electrochemical procedures in wastewater treatment is electrocoagulation. The electrochemical dissolution of sacrificial metal electrodes (iron or aluminum) into soluble or in soluble species, depending on the pH, is the basis of electrocoagulation (EC) (Sher et al. 2021). The electrochemical process involves using sacrificial soluble iron (Fe) and aluminum (Al) as anodes and/or cathodes to release metal ions by anodic oxidation. These ions combine with the cathode's produced aluminum hydroxide, resulting in flock formation. Under the application of alternating current to minimize the electrode passivation, it is one of the main disadvantages of electrocoagulation technique under direct current. The use of alternating current allows a more efficient process, with lower power consumption and sludge generation, in comparison with the process of EC (Kamaraj et al. 2013). As a result, the pulsed electrochemical process is more efficient at removing color and COD while using less energy than the (direct current electrocoagulation) DCE technique. However, for removing contaminants from industrial effluent, the pulsed electrochemical process is the best option. One of these techniques is electrochemical coagulation, which is the electrochemical reaction of destabilizing agents that cause charge neutralization for pollutant removal and has been employed in wastewater treatment (Vasudevan 2012). Because of their availability and inexpensive cost, iron and aluminum are the most commonly utilized electrode materials in the EC process (Zhang et al. 2021).

Pulsed-electrocoagulation treatment alone is an interesting and preprocessing method for removing hazardous and organic compounds using a technology that is effective, adaptable, cost-effective, simple, and clean (Bernal-Martínez et al. 2013; Tahreen et al. 2020; Ren et al. 2011). As a result, pulsed electrochemical (PEC) was successful in eliminating % color removal, % COD removal while using less electricity (Asaithambi et al. 2021). (Bian et al. 2019) The study conducted an investigation on the treatment of high salinity bilge water, employing both direct and alternating current-powered electrocoagulation processes. The results revealed that the utilization of constant alternating current exhibited superior performance in terms of sustaining consistent output levels while consuming less energy compared to the operation in direct current mode. (Othmani et al. 2017) added that, in comparison with the direct current electrocoagulation method, the alternating-current electrocoagulation technique had the greatest elimination of the colors methylene blue and indigo carmine while consuming less energy. (Eyvaz 2016) found that, in comparison with the direct current electrocoagulation technique, the alternating pulse current had better clearance rates in shorter working times.

Pulsed-electrocoagulation process (PECP) was employed to clean wet coffee processing wastewater (WCPWW) and repurpose it for a number of uses. This may ease the strain on groundwater and bodies of surface water. The goal of the wastewater treatment process is to produce cleaned effluent and sludge that can be disposed of without harming the environment (Hassen and Asmare 2018). The main objective of this study to investigate the effect of PECP to treat wastewater generated from wet coffee processing. To determine the removal efficiency of color, COD, turbidity, phosphate, nitrate, and power consumption. To analyze effects of independent variables on removal efficiency of color, COD, turbidity, phosphate, and nitrate by using RSM. To optimize and select the best removal efficiency of the pulsed electrochemical process for the treatment of coffee processing wastewater.

Material and methods

Chemical and reagents

Chemicals used in this investigation are mercury sulfate (HgSO4), ferrous ammonium sulfate (Fe(NH3) SO4), sulfuric acid (H2SO4), silver sulfate (Ag2SO4), ferroin indicator (Fe(o-phen)3 SO4), potassium dichromate (K2Cr2O7), hydrogen per oxide (H2O2), sodium sulfate (Na2SO4), KOH, NaOH, NaCl, sodium hydrogen carbonate (NaHCO3), phenolphthalein, stannous chloride, ammonium molbidate, phenol, buffer solution, and distilled water.

Experimental setup

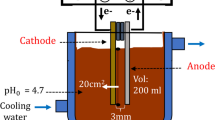
The goal of this experiment is to determine the contribution of pulsed-electrocoagulation processes in wastewater treatment, as well as to assess the efficiency of color, COD, turbidity, nitrate, and phosphate removal from coffee processing wastewater and by using aluminum (Al) electrode. The schematic arrangement of the experimental setup is shown in Fig. 1. The experiments were carried out in a 1 L batch mode electrochemical reactor with a pair of rectangular-shaped Al electrodes with a total area of 90 cm2. The electrodes were connected vertically with an adjustable gap of 1 cm between them and were powered by a DC/AC power supply in monopolar mode. The electrodes were thoroughly cleaned and washed with HCl and water for about 15 (min) before and after each run. The solution was continuously stirred using a magnetic stirrer at a constant speed. The pH of the wastewater was measured using pH meter and it was adjusted using a 0.1 N NaOH and H2SO4 solution. With required experimental conditions, the samples were collected from EC reactor and filtered using Whatmann 42 filter paper. The color, COD, turbidity, nitrate, and phosphate were determined to examine the behavior of PECP process for treatment of wastewater.

Fig. 1
figure 1

Experimental setup

Full size image

The experimental design and statistical analysis

Response surface methodology (RSM) is a technic tool for analyzing the relationship between the process variables and the responses (Sadaf et al. 2022). As a result, response is used to describe a performance metric or quality attribute. The input variables are also known as independent variables, and they are under the scientist’s or engineer’s control. The response surface approach is a set of strategies for using experimental methods to find the best operating conditions. Typically, this requires conducting a series of experiments and using the results of one to guide the following steps (Bähre et al. 2013; Akter and Islam 2022). In this study, laboratory experiments were carried out using a PECP by varying parameters in their interval pH (3–11), electrolyte concentration (0.3–0.6 g/L) of NaCl, current (0.5–1 Amp), and reaction time (30–60 min). Those parameters were considered to determine the removal efficiency of COD, color, turbidity, phosphate, and nitrate. The order of experiments was arranged randomly (Darvishmotevalli et al. 2019; AlJaberi et al. 2020; Sharma and Simsek 2020).

As shown in Table 1, these inputs give number of experimental runs, range of pH, time, current, and electrolyte which were generated by using RSM software.

Table 1 Experimental design
Full size table

Analysis

% COD removal

Equation (1) used to determine % of COD removal efficiency (Asaithambi et al. 2021).

$$\% {\text{COD removal}}, = \left( {\frac{{{\text{COD}}_{i - } {\text{COD}}_{t} }}{{{\text{COD}}_{i} }}} \right) *\left( {100} \right)$$
(1)

where CODi and COD0 are the COD (mg/L) at initial (i = 0) and at any reaction time (t), respectively.

% color removal

$$\% {\text{Color removal}}, = \left( {\frac{{{\text{Abs}}_{i - } {\text{Abs}}_{t} }}{{{\text{Abs}}_{i} }}} \right)*\left( {100} \right)$$
(2)

where Absi and Abst are absorbance of sample for corresponding weave length (ƛ = 420 nm) at initial (i = 0) and at any reaction time (t), respectively.

% turbidity removal

$${\text{Turbidity removal}}, = \left( {\frac{{{\text{Tur}}_{i - } {\text{Tur}}_{t} }}{{{\text{Tur}}_{i} }}} \right)*\left( {100} \right)$$
(3)

where Turi and Turt are the turbidity of the sample (NTU) at initial (t = 0) and at any reaction time (t), respectively.

% nitrate removal

$${\text{Nitrate removal}}, \% = \left( {\frac{{{\text{NO}}_{4\,i - }^{3} {\text{NO}}_{4\,t}^{3} }}{{{\text{NO}}_{4\,i}^{3} }}} \right)*\left( {100} \right)$$
(4)

where NO43i and NO43t are concentration of nitrate before and after treatment, respectively.

% phosphate removal

$${\text{Phosphate removal}}, \% = \left( {\frac{{{\text{PO}}_{4\,i - }^{3} {\text{PO}}_{4\,t}^{3} }}{{{\text{PO}}_{4\,i}^{3} }}} \right)*\left( {100 } \right)$$
(5)

where PO43i and PO43t are the concentration of phosphate before and after treatment, respectively.

Power consumption, (kWhr/m3)

On the practical and economic perspective, the consumption of electrical energy is an important factor in the alternating-current electrocoagulation (ACE) process and it was calculated using equation.

$${\text{Power consumption}} = \left( {\frac{{{\text{VI}}t}}{{V_{s} }}} \right)$$
(6)

where V cell voltage (volt), I applied current (amp), t—ACE treatment time (hr), and VS, volume of wastewater used (L).

Result and discussion

Characteristics of wastewater

Chemical characteristics of wet coffee processing, such as nitrate, phosphate, and COD, were analyzed, before treatment as well as physical parameters such as color and turbidity. According to the analysis, the color is very black with 2.042 abs, turbidity of 631NTU, pH of 4.5, COD of 2980 mg/L, phosphate of 17.45 mg/L, and nitrate of 14.491 mg/L.

Removal efficiency of Pulsed electrochemical process

Wastewater generated from coffee processing industry was treated in laboratory by considering effects of independent variables and using electrolytes with different charges as below.

Pulsed-electrochemical process by using NaCl

Sodium chloride (NaCl) is an electrolyte that is used to increase conductivity and decrease the amount of voltage supplied to wastewater during the treatment process by forming Na+ and Cl−. The addition of various concentrations of NaCl as a supportive electrolyte increases the conductivity of wastewater (Asaithambi et al. 2020).

Effect of operating parameters on % of removal efficiency

The operating parameter that has the greatest influence on PECP, such as solution pH, electrolyte concentration (NaCl), electric current, and reaction time, was investigated in the terms of percent COD, color, turbidity, NO3, and PO3 removal at room temperature. The removal efficiency of % color, COD, and turbidity, nitrates and phosphate with an energy consumption using PECP are shown in Table 2, which is based on the Al–Al electrode combination with its respective predicted values from RSM.

Table 2 Full-centered composite design for color, COD, turbidity, PO43, and NO43, removals
Full size table

Optimization of response surface methodology

Response surface methodology is a type of regression analysis that predicts the value of a dependent variable based on the controlled values of the independent variables (Sadaf et al. 2022). RSM was used to optimize an experimental parameter for another process, which included electrochemical oxidation. It is a highly efficient procedure because it not only determines the best operating conditions to maximize system performance, but it also generates a response surface model that predicts a response based on a combination of factor levels. It also depicts the magnitude and impact of various factors on the response, as well as their interactions. As a result, they have been used to simulate a variety of water and wastewater treatment systems and processes (Asaithambi and Matheswaran 2016).

Estimation models were used to optimize the responses in order to determine optimal points for operational conditions and achieve the highest removal percentage. COD, color, turbidity, nitrate, and phosphate removal percentages were set to their maximum values to achieve the best removal performance under operational conditions and the results are given in Table 3. In the in-range state, the target values of four independent variables, including reaction time, solution pH, electric current, and electrolyte, are observed. The following were the optimal conditions for independent variables: pH = 7, reaction time of 45 min, electric current of 0.45 Amp, salt concentration of 0.75 g/L. Under these conditions, the model’s degree of desirability was equal to one, while the removal % of COD, color, and turbidity.

Table 3 Optimum value of pollutant removed by pulsed electrochemical process
Full size table

Analysis of variance

Analysis of variance (ANOVA) was used to determine the interaction between the process factors and the response in graphical data analyses. The R2 value was used to describe the quality of the fit polynomial model, and the F test was used to determine its statistical significance. With a 95% confidence level, the P value (probability) was used to evaluate model terms. The data was examined using the analysis of variance (ANOVA), which includes descriptive statistics and statistical tests. This test is used to determine the effect of all variables on the intended response. ANOVA is a statistical method for testing hypotheses about model parameters by dividing total variance in a set of data into smaller groups and component portions that are linked to specific sources of variation (Bui 2017). ANOVA was used to determine significant values between input factors and responses. To determine whether the recommended design is consistent with the test data, statistical factors such as R2, Adj. R2, F-test value (F value), and probability value must be examined (p value). The higher the F value and the lower the P value, the greater the significance of the corresponding term in the recommended correlation for response, so a P value less than 0.05 is considered significant. The mean squares values were calculated by dividing the sum of each variation source’s squares. To avoid systemic error, the experiments were conducted at random. The coefficients of the second-order model, which interpret the amount of removal of the investigated parameters (responses), determine the performance of independent variables (factors). To identify key terms in the model, surface response analysis looks for low p values. The ANOVA results for responses with p < 0.05 probability values show that the second-order model is significant. The mean squares values were calculated by dividing the sum of the squares of each variation source by their degrees of freedom, and the statistical significance was determined in all analyses using a 95 percent confidence level (0.05).

According to Table 4, ANOVA for the % removal of COD by quadratic model is observed. The Model F value of 41.04 implies that the model is significant. There is only a 0.01% chance that an F value this large could occur due to noise. P values less than 0.0500 indicate that model terms are significant. In this case, A, B, C, D, A2, B2, and D2 are significant model terms. Values greater than 0.1000 indicate that the model terms are not significant. The lack of fit F value of 2.59 implies that the lack of fit is not significant relative to the pure error. There is a 15.22% chance that a lack of fit F value this large could occur due to noise. Nonsignificant lack of fit is good.

Table 4 ANOVA for the % removal of COD by quadratic model
Full size table

According to Table 5, ANOVA for the % removal of turbidity by quadratic model is observed. The Model F value of 451.28 implies the model is significant. There is only a 0.01% chance that an F value this large could occur due to noise. P values less than 0.0500 indicate model terms are significant. In this case, A, B, C, D, A2, B2, C2, and D2 are significant model terms. Values greater than 0.1000 indicate that the model terms are not significant. The lack of fit F value of 4.18 implies that there is a 6.40% chance that a lack of fit F value this large could occur due to noise.

Table 5 ANOVA for % removal of turbidity by quadratic model
Full size table

According to Table 6, ANOVA for the % removal of nitrate by quadratic model is observed. The Model F value of 221.87 implies the model is significant. There is only a 0.01% chance that an F value this large could occur due to noise. P values less than 0.0500 indicate model terms are significant. In this case, A, B, C, D, AC, AD, A2, and D2 are significant model terms. Values greater than 0.1000 indicate that the model terms are not significant. The lack of fit F value of 4.18 implies that there is a 6.38% chance that a lack of fit F value this large could occur due to noise.

Table 6 ANOVA for % removal of nitrate by quadratic model
Full size table

According to Table 7, ANOVA for the % removal of phosphate by quadratic model is observed. The Model F value of 562.48 implies the model is significant. There is only a 0.01% chance that an F value this large could occur due to noise. P values less than 0.0500 indicate model terms are significant. In this case, A, B, C, D, A2, B2, C2, and D2 are significant model terms. Values greater than 0.1000 indicate that the model terms are not significant. The lack of fit F value of 4.06 implies that there is a 6.77% chance that a lack of fit F value this large could occur due to noise.

Table 7 ANOVA for % removal of phosphate by quadratic model
Full size table

According to Table 8, ANOVA for the % removal of color by quadratic model is observed. The Model F value of 31.54 implies the model is significant. There is only a 0.01% chance that an F value this large could occur due to noise. P values less than 0.0500 indicate model terms are significant. In this case, A, B, C, D, A2, and B2 are significant model terms. Values greater than 0.1000 indicate that the model terms are not significant. The lack of fit F value of 3.58 implies there is a 8.61% chance that a lack of fit F value this large could occur due to noise.

Table 8 ANOVA for % removal of color by quadratic model
Full size table

Fit statistics

The statistical significance of the model equation and model terms was determined using ANOVA. According to (Darvishmotevalli et al. 2019), model fitting quality was controlled using determination coefficients (R2 and Adj. R2), while statistical significance was controlled using the Fischer test (F-test). The model was validated using predicted R-squares (R2), which employs the leave-one-out technique to assess the model’s prediction power in the face of new observations. Coefficients are used to quantify the relationship between experimental and expected responses (R2). The coefficient of determination (R2) is defined as the ratio of total changes in the expected response caused by the model variables. Show the ratio of sum of squares regression to total sum of squares. R2 should be large and close to 1, and there should be a desired correspondence with adjusted R2 (Adj.R2). R2 expresses the fitness quality of a second-order polynomial model. According to (Mirhosseini et al. 2009), the model’s goodness of fit was also assessed using coefficients of determination R2 (correlation coefficient) and adjusted coefficients of determination R2adj. The high value of the correlation coefficient R2 = 0.9707 indicated that the model was highly reliable in predicting removal percentages, with the model explaining 97.07 percent of the response variability. In this study, all of the R2 values were greater than 0.9. According to (Thirugnanasambandham et al. 2015) for a satisfactory model fitness, R2 should be at least 0.8. R2 values greater than one indicate a high level of agreement between experimental and model-estimated data. As a result, in this study, high R2 values and their agreement with Adj are examined. The value of R2 indicates that the model is highly significant. Table 9 show the “signal-to-noise ratio” index as adequate precision (AP). In other words, AP compares the predicted range of values at design points to the mean prediction error.

Table 9 Model summary for % COD removals
Full size table

The predicted R2 of 0.8712 is in reasonable agreement with the Adjusted R2 of 0.9508; i.e., the difference is less than 0.2. Adeq precision measures the signal-to-noise ratio. A ratio greater than 4 is desirable. Ratio of 28.624 indicates an adequate signal. This model can be used to navigate the design space.

Effect of model parameter and their interactions

The most useful method for revealing reaction system conditions is to use 3D surfaces and 2D contour plots, which are graphical representations of the regression equation for optimizing reaction conditions. They are also used to see how each variable influences the results. In such quadratic model plots, the response functions of two elements are depicted by varying within the experimental ranges, while all other factors are held constant at their values. According to the findings, all of the combined process variables had a significant effect on color, COD, turbidity, nitrate, and phosphate removal with their power consumption in the treatment process. The three-dimensional response surface analysis of the independent variables and the dependent variable was used to estimate the optimal values of the operation parameters. A series of three-dimensional (3D) response surface graphs were created and are shown in Figure below to demonstrate the relationship between removal efficiency and factors.

Interaction of pH and current

The removal COD efficiency was low at pH 3 and increased too much at neutral pH, as indicated by the red color and when the current was around 0.45Amp, according to the 3D graph in Fig. 2. As a result, there was a significant interaction between pH and current. The initial pH and current interacted significantly in the removal of COD in the PEC process. Figure 2 shows that increasing the current density from 0.3 to 0.6 Amp and increasing the pH from acidic 3 to neutral 7 have a positive effect on COD removal. The mutual interaction effect of current density, on the other hand, was critical in the removal of COD and color in the PEC process (Shahedi et al. 2020; Sharma and Simsek 2020).

Fig. 2
figure 2

Interaction effect of pH with current plots for % removal of COD

Full size image

Interaction of current and time

The color removal efficiency was high at 0.45Amp, which is indicated by red color, and when the time is 45 min. Increasing time up to the center of the graph and increasing time in the same way, it comes to the red color where it shows the high removal efficient; terminal points indicated by green color shows lower removal efficiency, indicating that the interaction effect of current and time was significant. Through contour plots and 3D response surface plots, the mutual effects of current density and time as an estimate of response removal efficiency are shown Fig. 3 EC processes. Current density and time interacted in the PEC process to achieve significant color and COD removal. Because of anodic dissolution in accordance with Faraday’s law, the removal efficiency was increased as the current density was increased. The impact of applied current on the quantity of Fe ions discharged from electrodes, as well as the release of gas bubbles and the formation of flocs. The effect of applied current should be considered in any EC approach for wastewater treatment (Shahedi et al. 2020; Sharma and Simsek 2020). The quantity of Al released from electrodes is directly influenced by electrolysis time, in which turn the effects amount of Al released from the anode and determined the COD, color, and nutrient removal efficiency (Othmani et al. 2022).

Fig. 3
figure 3

Interaction effect time with pH plot for % removal of color

Full size image

Interaction of pH and electrolyte

Figure 4 graph shows that color removal efficiency increased as pH increased from lower to higher; maximum removal at neutral was indicated by more red color, but it decreased after and before neutral pH. It also shows a small increase in removal efficiency from a low electrolyte dosage to the maximum, followed by a decrease at the maximum dosage. The increase in NaCl concentration enhances the generation of oxidizing agents, resulting in increased pollutant removal. Even if the concentration of NaCl varies, the removal efficiency of pollutants is increased with increase in the concentration of NaCl (Othmani et al. 2022). The interaction effect of pH and electrolyte is only marginally significant in the color removal process.

Fig. 4
figure 4

Interaction effect electrolytes with pH plot for % removal of color

Full size image

Regression equation

Regression analysis is one of the most commonly used statistical techniques in social and behavioral sciences as well as physical sciences, and it entails identifying and evaluating the relationship between a dependent variable and one or more independent variables, also known as predicator or explanatory variables. It is especially useful for assessing and adjusting for confounding variables. The relationship model is hypothesized, and parameter estimates are used to develop an estimated regression equation. Various tests are then used to determine whether or not the model is satisfactory (Akter and Islam 2022). (Mirhosseini et al. 2009) If the model is satisfactory, the estimated regression equation can be used to predict the value of the dependent variable given the independent variable values. Regression analysis is used to explain variability in dependent variable by means of one or more of independent or control variables and to analyze relationships among variables to answer; the question of how much dependent variable changes with changes in each of the independent’s variables, and to forecast or predict the value of dependent variable based on the values of the independent’s variables.

The experimental results were analyzed using multiple regressions, and the empirical relationship between the response and independent variables was expressed using a second-order polynomial equation. Two empirical models were created to better understand the interactive relationship between responses and process variables (Thirugnanasambandham et al. 2015; Akter and Islam 2022). As a result, the experiment was evaluated in terms of pH (A), reaction time (B), applied current (C), and supporting electrolytes (D). All influencing factors were optimized in order to determine optimal operating conditions for maximum color, COD, nitrate, phosphate, and turbidity removal efficiency with minimum power consumption in the pulsed electrochemical process. NaCl was used to achieve an empirical relationship between the response and the independent variables, which could be approximated by a quadratic polynomial as follows:

$$\begin{aligned} {\text{COD}} = & + \,97.66 + 3.59A + 0.7536B + 0.6929C + 0.6027D - 0.0816AB \\ & - \,0.1365AC - \,0.4241AD + 0.5489BC + 0.0754BD - 0.3553CD - 3.94A^{2} \\ & - \,1.04B^{2} - \,0.1654C^{2} - \,0.6321D^{2} \\ \end{aligned}$$
(7)
$$\begin{aligned} {\text{Color}} = & + \,97.85 + 4.61A + 0.6655B + 0.2114C + 0.7272D \\ & + 0.1681AB - 0.2788AC - 0.9414AD - 0.0536BC - 0.4211BD \\ & - 0.9008CD - 4.513A^{2} - 0.133B^{2} - 0.4812C^{2} + 0.0786D^{2} \\ \end{aligned}$$
(8)
$$\begin{aligned} {\text{Turbidity}} = & + \,98.63 + 4.29A + 0.4270B + 0.2981C + 0.5883D + 0.0199AB \\ & + \,0.2394AC + 0.0820AD - 0.0453BC - 0.2273BD + 0.0239CD \\ & - \,5.37A^{2} - 0.2379B^{2} - 0.6566C^{2} - 0.4146D^{2} \\ \end{aligned}$$
(9)
$$\begin{aligned} {\text{Phosphate}} = & + \,98.91 + 4.77A + 0.6490B + 0.4775C + 0.2585D + 0.0372AB \\ & + \,0.1042AC + 0.0075AD - 0.1006BC + 0.1733BD + 0.1047CD \\ & - \,5.30A^{2} - 0.4270B^{2} - 0.1746\,C^{2} - 0.3089D^{2} \\ \end{aligned}$$
(10)
$$\begin{aligned} {\text{Nitrate}} & + 98.11 + 4.80A + 0.4871B + 0.3141C + 0.4749D - 0.1857AB \\ & - 0.3818AC - 0.4472AD - 0.1291BC - 0.2895BD - 0.1745CD \\ & - 4.78A^{2} - 0.2576B^{2} - 0.2615C^{2} - 0.1762D^{2} \\ \end{aligned}$$
(11)

The equation in terms of coded factors can be used to predict response for different levels of each factor. The high levels of the factors are coded as + 1 by default, while the low levels are coded as − 1. By comparing the factor coefficients, the coded equation can be used to determine the relative importance of the factors.

The models’ terms are organized using a coding system. The ANOVA test was used to determine the model’s suitability. As shown in the tables above, the lack of fit test was used to confirm model validity. The ANOVA for lack of fit was insignificant (P < 0.05) on the regression model. All of the results show that this model fits the experimental data well. Due to the higher percentage COD, color, nitrate, phosphate, and turbidity removal value and better extraction yield in the shortest time, these findings indicate that PECP was the most effective method for wastewater treatment. Significant differences (P ≤ 0.05) are indicated by means with different letters within the same row.

The desired optimum condition for response

Figure 5 shows that at the optimum levels, the prediction and experimental findings are in good agreement and in line with the straight line, indicating that the model is very valid. According to RSM, the expected R2 for this initial model was 98.91 percent. The backward elimination method was used to construct a parsimonious model with meaningful predictors. The coefficient of determination of the anticipated model revealed a quadratic relationship between responses and parameters with a good regression coefficient.

Fig. 5
figure 5

The comparison of predictive and the experimental result for the PECP by using NaCL the optimum value on removal efficiency

Full size image

The optimum PECP conditions were determined as a practical optimum using Design Expert 11.1.2.0 software: electrolysis time of 45 min, salt concentration of 0.75 g/L, and pH of 7. To further validate the predictability of the theoretical model, verification experiments were carried out under optimal conditions. The results showed that experimental removal efficiencies were very close to predicted values, with a difference of less than 0.2 and no significant differences (P > 0.05). As a result, it was possible to conclude that the established model in this study was appropriate and valid. The diagrams a, b, c, and d show the actual and predicted values of NO43, color, PO43, and COD which are not dispersed from each other and in line with the straight line.

Furthermore, the model’s adequacy can be evaluated using diagnostic diagrams including normal probability distribution diagram of residuals, the diagram of predicted values versus real values. Figures 6, 7 and 8 show the distribution of normal probability percentage versus student zed residuals for COD, turbidity, and phosphate removal levels. The points in these diagrams are arranged in a relatively straight line, indicating that the variance and normal distribution are constant. The points in the normal probability distribution diagram of residuals are almost straight line aligned. Some of the scattered points are even expected in the data’s normal distribution. The figures show that there are no outliers that cross the red line.

Fig. 6
figure 6

Distribution of normal probability percentage and residuals for COD

Full size image
Fig. 7
figure 7

Distribution of probability percentage and residuals for Turbidity

Full size image
Fig. 8
figure 8

Distribution of normal probability percentage and residuals for phosphate

Full size image

The results of removal efficiency were closer to the straight line on the distribution of probability percentage and residuals graphs for pollutant removal, as shown in shown in Figs. 8a, b. The number of externally studentized residuals on the second graph run varied uniformly, where the experiment results are valid.

Conclusion

Pulsed-electrocoagulation process for the treatment of coffee processing wastewater was the newest technology with consumed low power consumption. By using the PECP, operating parameters such as pH, electrolyte concentration, electrolysis time, and current play a major role on pollutant and nutrient removal efficiency. As a result, by using the NaCl as an electrolyte concentration, the maximum removal efficiency of color, COD, turbidity, phosphate, and nitrate was 99.92%, 98.75%, 99.00%, 99.02%, 98.83% obtained, respectively, with the pH of 7, reaction time of 45 min, electrolyte concentration of 0.75 g/L, and current of 0.45Amp with total power consumption is 0.972 kWh/m3.

The response surface methodology was used to analyze a large number of experimental runs while producing multiple outputs based on variables such as pH, reaction time, current, electrolyte concentration, and responses such pollutant and nutrient removal. The analysis of variance (ANOVA) with 95 percent confidence limits was used to test the significance of independent variables and their interactions. The quadratic regression equation was recommended as a good model for predicting color, COD, turbidity, phosphate, and nitrate removal efficiency. The model’s goodness of fit was validated with high values of squared correlation coefficient for each of color, COD, turbidity, phosphate, and nitrate. This study suggests that the PECP process could be a successful alternative treatment process for coffee processing wastewater when compared to traditional treatment methods such physicochemical process. As a result, it is concluded that this treatment technology can be used on a large scale to treat the coffee processing wastewater and industrial effluent.