Introduction

A combined weir–orifice structure can be utilized for discharge measurement in the open channels with different shapes when the flow has high suspended load (Vatankhah and Khalili 2020). In this system, the flow passes simultaneously over the weir and below the orifice. As a result, for a constant upstream head, the volume of water passing through a weir–orifice is higher than the flow over a weir with the same dimensions (Salehi and Azimi 2019). It is essential to know the volume of water passing through the hydraulic structures installed in the irrigation canals for agricultural water management. Therefore, accurate estimation of the discharge coefficient (Cd) of the measurement devices is very important.

Some of researchers have conducted experiments to determine Cd of the combined weir–orifice (Majcherek 1984; Alhamid 1999; Ferro 2000; Negm et al. 2002; Hayawi et al. 2008; Samani and Mazaheri 2009; Altan-Sakarya and Kökpınar 2013; Severi et al. 2015). They presented empirical relations or diagrams for predicting the discharge of the combined flow.

Fu et al. (2018) performed 284 experimental tests to study the hydraulic characteristics of combined weir–orifice. They derived a functional equation using dimensional analyses between the weir–orifice Cd and contributing parameters including water level, orifice height, weir–orifice length, and weir–orifice length.

Salehi and Azimi (2019) investigated the simultaneous flow over and below different weir–orifice structures located in rectangular channels using dimensional analysis and multivariable regression techniques. They classified seven weir–orifice structures based on the shape and geometry. Also, they developed general empirical equations to estimate the critical head using the non-dimensional geometry parameters and hydraulic characteristics of weir–orifice structures.

Vatankhah and Khalili (2020) introduced a sharp-edged plate installed at the end of a circular channel under free outflow conditions. They deduced stage–discharge relationships using the energy principle and dimensional analysis for the weir–orifice system.

Although the experimental studies provide precise and exact visions for the researchers about flow conditions in prototype of hydraulic structures, the laboratory tests carried out are time-consuming and expensive. In the last two decades, incorporation of the soft computing and different types of the intelligent models (e.g., ANN, ANFIS, and SVM) have been accepted as an efficient alternative for simulating flow in open channels (Haghbin and Sharafati 2022). In this regard, artificial intelligence (AI) models have been successfully implemented for predicting the Cd of flow measurement structures (i.e., weir, gate, and orifice).

Ebtehaj et al. (2015) defined five different scenarios by using non-dimensional variables affecting on the discharge of rectangular side orifices and applied successfully the group method data handling (GMDH) to predict the Cd.

Azimi et al. (2017) used the hybrid of genetic algorithm (GA) and ANFIS (GA-ANFIS) to predict the Cd of a rectangular side orifice. They also simulated the flow through the orifice by applying computational fluids dynamic (CFD). Their outcomes showed that the hybrid GA-ANFIS model had better performance than CFD model.

Parsaie et al. (2018) utilized ANN, SVM and GMDH-PSO techniques for predicting the Cd of a cylindrical weir–gate. They observed that all developed models had good performance.

Azimi et al. (2019) forecasted the Cd of rectangular side weirs located on the trapezoidal open channels via the support vector machine (SVM). They presented six different models based on the effective variables and introduced the most powerful model for predicting the Cd of side weirs.

Jamei et al. (2021) developed three linear data-driven models including locally weighted learning regression (LWLR), multiple linear regressions with interaction (MLRI), and multivariate linear regression (MLR) for predicting the Cd of a sharp-crested triangular side orifice under a free flow condition. They detected that MLRI and LWLR had similar suitable performance for modeling the Cd values.

Karbasi et al. (2021) employed two kernel-based paradigms, namely kernel extreme learning machine (KELM) and Gaussian process regression (GPR) along with response surface methodology (RSM) and generalized regression neural network (GRNN) to estimate the Cd of elliptical side orifice in rectangular channels. They found that the learning machine models used in their research had good performance compared to the regression-based equations.

Moghadam et al. (2022) attempts to recreate the Cd of triangular side orifices by a new training method named Regularized Extreme Learning Machine (RELM). They extended six RELM models based on the influencing parameters. The efficiency of the best RELM model were compared with the ELM and it was demonstrated that the RELM is noticeably stronger.

Hasnai and Shabanlou (2022) established an artificial intelligence procedure entitled Outlier Robust Extreme Learning Machine (ORELM) for ascertaining the Cd of side slots. They determined five ORELM models by executing a sensitivity analysis. Finally, they introduced the superior model and the most impacting parameters to reproduce the Cd of side slots.

More recently, Khosravinia et al. (2023) predicted Cd of triangular (Δ-shaped) side orifice by applying three data-driven models including SVM, LSSVM and LSSVM improved by gravity search algorithm (LSSVM-GSA). Five different scenarios were applied based on the dimensionless variables. The results showed that all of the applied models estimated the Cd of Δ-shaped side orifice with adequate accuracy.

The Cd of combined weir–gate structure has been also successfully predicted using AI models (Parsaie et al. 2016, 2019; Parsaie and Haghiabi 2020).

To the best of our knowledge, limited researches have been done to use the AI models to predict the Cd of combined weir–orifices. In this research, for recreating the Cd of weir–orifices located in circular channel, we integrated evolutionary algorithms including gravitational search algorithm (GSA) and particle swarm optimization (PSO) with adaptive neuro-fuzzy interference system (ANFIS). The efficiency of the presented model (ANFIS-PSO-GSA) was compared with the ANFIS-PSO, ANFIS-GSA, and ANFIS.

Materials and methods

Analyzing discharge coefficient of a weir–orifice structure

According to the analytical relations provided by Vatankhah and Khalili (2020), the effective parameters in the discharge coefficient of the weir–orifice structure can be expressed as follows:

$$Cd={f}_{1}\left(Q,D,H,W,h,g,\sigma ,\mu ,\rho \right)$$
(1)

These parameters are discharge (Q), channel diameter (D), plate height (H), orifice opening height (W), upstream water depth (h), gravity acceleration (g), water surface tension (σ), dynamic viscosity (μ) and water density (ρ).

By applying the Buckingham’s theorem, Eq. (1) is expressed as follows:

$$\frac{Q}{\sqrt{g{D}^{5}}}={f}_{2}\left(\frac{H}{D}, \frac{W}{D},\frac{h}{D},\frac{\rho D\sqrt{gh}}{\mu },\frac{\sigma }{\rho g{h}^{2}}\right)$$
(2)

Due to insignificant influence of Reynolds and Weber number, these two parameters have been neglected:

$$\frac{Q}{\sqrt{g{D}^{5}}}={f}_{3}\left(\frac{H}{D}, \frac{W}{D},\frac{h}{D}\right)$$
(3)

In current study, we investigate impact of dimensionless parameters of Eq. 3 on discharge coefficient of weir–orifice structure using data-driven models.

Experimental data

In present study, the experimental data of flow discharge of weir–orifice structure given by Vatankhah and Khalili (2020) were utilized for developing the models in the training and validation stages. Figure 1 shows the sketch of experiments with the measured parameters.

Fig. 1
figure 1

Sketch of flow over combined weir–orifice structure (Vatankhah and Khalili 2020)

Full size image

A total of 626 data with 46 geometric configurations were utilized in the present study consisting of two different diameter pipe D = 19.1 cm and D = 30.1 cm under free outflow conditions. Experiments were performed in the pipe A with D = 19.1 cm for five plate heights (H = 3.3, 4, 5, 6.4 and 8 cm) and five orifice heights (W = 3, 4, 5, 6 and 7 cm). In addition, experiments were conducted in the pipe B with D = 30.1 cm for five plate heights (H = 5, 6, 7.5, 10 and 12 cm) and five orifice heights (W = 4, 5, 6, 7 and 8 cm). Among 626 data points, 243 data points are from small pipe A with D = 19.1 cm, whereas 383 data points are from bigger pipe B with D = 30.1 cm. The flow discharge in experiments was between 2.43 and 40.62 L/s. Some statistical information of the input data is presented in Table 1. According to Table 1, the range of experimental parameters were \(0.31\le \frac{h}{D}\le 0.93\), \(0.13\le \frac{W}{D}\le 0.37\) and \(0.16\le \frac{H}{D}\le 0.42.\) In the table, xmin, xmax, xmean, Sx and Csx indicate the minimum, maximum, mean, standard deviation and skewness coefficients.

Table 1 Statistical parameters of experimental data used in the study
Full size table

Adaptive neuro-fuzzy inference system (ANFIS)

The ANFIS is similar to a multilayer neural network, except that in addition to neural network learning algorithms, it also uses fuzzy logic (Jang 1991). Fuzzy theory, developed by Takagi, Sugeno (1985), is able to mathematically formulate many complex and ambiguous concepts, variables, and systems, providing the basis for reasoning, control, and decision-making in conditions of uncertainty. ANFIS model consists of five layers including information input layer, fuzzy rules weight calculation layer, normalization layer of the weights of the obtained rules, rule calculation layer, summation layer and network output, respectively (Shamshirband et al. 2019; Sanikhani and Kisi 2012). One of the important properties of ANFIS is the ability of hybridizing learning algorithms of the backpropagation slope method and the least squares method in order to modify the parameters (Baghban et al. 2016; Kisi et al. 2015). Figure 2 shows a schematic of the model and layers with two inputs and one output.

Fig. 2
figure 2

ANFIS structure diagram

Full size image

Particle swarm optimization (PSO)

Particle swarm optimization algorithm is nature-inspired and on the basis of bird feeding behavior. This method is based on random population launches and repetitive search updates. Over time, particles accelerate toward particles that have a higher suitability criterion (Kennedy 2010). The PSO algorithm includes three steps: generating particle positions and velocity, updating the velocity, and finally updating the position. In this algorithm, a particle changes position based on a speed update in space (Hu et al. 2017).

The particles can record their present the global best position (gbest) and best position (pbest) in the search process. In addition, the particle velocity and position are computed by the following equations:

$${v}_{i}^{t+1}=w. {v}_{i}^{t}+{c}_{1}. {\text{rand}}. \left(p{\text{best}}-{x}_{i}^{t}\right)+{c}_{2}. {\text{rand}}. \left(g{\text{best}}-{x}_{i}^{t}\right)$$
(4)
$${x}_{i}^{t+1}={x}_{i}^{t}+{v}_{i}^{t+1}$$
(5)

where \({v}_{i}^{t+1}\) and \({x}_{i}^{t+1}\) are the ith particle velocity and position at the tth iteration, c1 and c2 are coefficients of acceleration controlling the effect of pbest and gbest during the search procedure, respectively, p(t) is the present best position of all the particles at the tth iteration, gbest is the best position between all the particles at whole iterations, w is the inertia weight and rand is a random number in the range [0, 1].

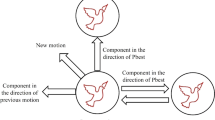
Therefore, the new position of the particle is a combination of moving in the direction of the previous particle velocity, the best experienced personal area of the particle, and the best experienced position of the sum (Fig. 3).

Fig. 3
figure 3

PSO algorithm diagram

Full size image

Hybrid of ANFIS-PSO

This model can enable adaptive learning through the ANFIS model with particle swarm-inspired techniques. In addition, in this model, the variables of the membership functions are optimized using the particle swarm technique (Basser et al. 2015; Azad et al. 2020).

First, using a completely random distribution function, the initial values of particle vectors and velocity vectors are obtained. The pbest value for each particle is taking to account equal to the current particle in the first iteration. By comparing the value of objective for each particle and considering the maximum value, the foremost position of particle can be obtained in the set of swarm (gbest).

The ANFIS model is run in different time steps. Therefore, the time series cab be simulated and considered as output for the model. The amounts calculated for the simulated and observed results are compared to each other (Robati and Iranmanesh 2020). For the second repetition, considering the gbest and pbest quantities and also velocity and situation of particles in previous step (i.e., first iteration) and with respect to Eqs. 4 and 5, the speed of new stage for particle is calculated.

The objective function values for each particle were generated for the second repetition as the same as the first repetition. The pbest is determined with comparison of values of the objective function with those obtained in the first iteration. When the particle’s position in the recent step was better than prior step, then the value of pbest of that particle is selected as the best status. For this step, this status could be the foremost one encountered for all particles as gbest. Therefore, pbest and gbest corresponds of each stage were determined according to previous stage values. Furthermore, updating of the velocity values and vectors can be done with respect to the particle position the recent stage. Eventually, the gbest of previous stage is considered as the best situation and corresponding value of parameter as the response at the end of the previous iteration step (Rini et al. 2016). Figure 4 shows the flowchart of ANFIS-PSO model.

Fig. 4
figure 4

ANFIS-PSO flowchart

Full size image

Gravitational search algorithm (GSA)

The GSA is a new algorithm developed on the basis of the gravity law by Rashedi et al. (2009). The agents in GSA attract each other by the gravity force. The quality of the agent is enhanced when the force of gravity increase. Therefore, the optimal solution is taken as the position of the agent with the largest mass. If there are N agents with d-dimension, the position of the ith agent is defined as follows:

$${X}_{i}=\left({x}_{i}^{1},{x}_{i}^{2},\dots ,{x}_{i}^{d} \right) \left(i=\mathrm{1,2},\dots N\right)$$
(6)

The gravity force acting on the ith agent from the jth agent at the tth time is obtained as follows:

$${F}_{ij}^{d}=G\left(t\right)\frac{{M}_{i}\left(t\right){M}_{j}\left(t\right)}{{R}_{ij}\left(t\right)+\varepsilon }\left({x}_{j}^{d}\left(t\right)-{x}_{i}^{d}\left(t\right)\right)$$
(7)

where G(t) is the gravitational constant at the tth time, Mj(t) and Mi(t) are the masses of the jth and ith the agent, respectively, Rij is the Euclidian distance between the ith agent and the jth agent, and ε is a constant with slight value. (Parsopoulos et al. 2005).

At the tth time, total gravity force acting on the ith agent is obtained as follows:

$${F}_{i}^{d}\left(t\right)=\sum_{j=1,j\ne 1}^{N}{\text{rand}}. {F}_{ij}^{d}\left(t\right)$$
(8)

where rand is a uniform random variable in the range [0,1]. On the basis of the motion law, the agent acceleration at the tth time is defined by following equation:

$${a}_{i}^{d}\left(t\right)=\frac{{F}_{i}^{d}}{{M}_{i}(t)}$$
(9)

The ith agent’s velocity and position are updated in each iteration process as follows:

$${v}_{i}^{d}\left(t+1\right)={\text{rand}}\times {v}_{i}^{d}\left(t\right)+{a}_{i}^{d}(t)$$
(10)
$${x}_{i}^{d}\left(t+1\right)={x}_{i}^{d}\left(t\right)+{v}_{i}^{d}\left(t+1\right)$$
(11)

where rand is a uniform random variable in the range [0, 1] and \({x}_{i}^{d}(t)\) and \({v}_{i}^{d}(t)\) are its current position and velocity, respectively (Hu et al. 2017).

Hybrid of ANFIS-PSOGSA

In the GSA model, population data are not shared with each other and therefore have a weak potential of development. By applying of the searching potential of GSA and PSO, each agent by the acceleration of GSA and the velocity of PSO is updated. The method is called PSOGSA. The following equations show the updated of ith agent’s velocity and the position:

$$v_{i}^{t + 1} = w. v_{i}^{t} + c_{1}^{\prime } . {\text{rand}}. ac_{i} \left( t \right) + c_{2}^{\prime } .{\text{ rand}}. \left( {g{\text{best}} - x_{i}^{t} } \right)$$
(12)
$${x}_{i}^{t+1}={x}_{i}^{t}+{v}_{i}^{t+1}$$
(13)

where w,\({v}_{i}^{t}\), \({x}_{i}^{t}\) and aci(t) are the inertia weight, the velocity, current position, and acceleration of the ith agent at the tth iteration, respectively. Also, \(c_{1}^{\prime }\) and \(c_{2}^{\prime }\) are constant acceleration coefficients.

In the present research, the \(c_{1}^{\prime }\) and \(c_{2}^{\prime }\) are considered as the exponential functions, as follows:

$$c_{i}^{\prime } = c_{{{\text{start}}}} . \left( {\frac{{c_{{{\text{end}}}} }}{{c_{{{\text{start}}}} }}} \right)^{{\frac{1}{{\left( {1 + k/T_{\max } } \right)}}}}$$
(14)

where cstart and cend are the initial and final values, k and Tmax are the current iteration number and the maximum iteration number, respectively. Figure 5 shows the steps of the algorithm.

Fig. 5
figure 5

ANFIS-PSOGSA algorithm diagram

Full size image

Assessment of the methods

The accuracy of new ANFIS method improved by PSOGSA is searched in modeling dimensionless experimental discharge (DED), and its outcomes are compared with hybrid ANFIS-PSO, ANFIS-GSA and standalone ANFIS. The following assessment criteria are employed:

$${\text{RMSE}}:\;{\text{Root}}\;{\text{Mean}}\;{\text{ Square}}\;{\text{ Error}} = \sqrt {\frac{1}{N}\mathop \sum \limits_{i = 1}^{N} [(Y_{0} )_{i} - (Y_{C} )_{i} ]^{2} }$$
(15)
$${\text{MAE}}:\;{\text{Mean }}\;{\text{Absolute}}\;{\text{ Error}} = \frac{1}{N}\mathop \sum \limits_{i = 1}^{N} |(Y_{0} )_{i} - (Y_{C} )_{i} |$$
(16)
$${\text{NSE}}:{\text{Nash}}-{\text{Suutcliffe}}=1-\frac{{\sum }_{i=1}^{N}[({Y}_{0}{)}_{i}-({Y}_{c}{)}_{i}{]}^{2}}{{\sum }_{i=1}^{N}[({Y}_{0}{)}_{i}-{\overline{Y}}_{0}{]}^{2}},-\infty <{\text{NSE}}\le 1$$
(17)
$${R}^{2}:\mathrm{Determination Coefficient}={\left[\frac{{\sum }_{t=1}^{N}\left({Y}_{o}-\overline{{Y}_{o}}\right)\left({Y}_{c}-\overline{{Y}_{c}}\right)}{\sqrt{{\sum }_{t=1}^{N}({Y}_{o}-\overline{{Y}_{o}}{)}^{2}({Y}_{c}-\overline{{Y}_{c}}{)}^{2}}}\right]}^{2}$$
(18)

where \({Y}_{c}, {Y}_{o}, {\overline{Y}}_{o}, N\) respectively refer to computed, observed, mean of the observed DED and data number.

Results and discussion

The parameters of the methods used in model development are provided in Table 2. For the PSOGSA, same control parameters with the PSO and GSA were set, and all algorithms were run 10 times to obtain more robust outcomes. Data of pipe A and pipe B were split in two parts training (first 80%) and testing (second 20%) for model applications. Testing dataset is selected on the basis of k-fold cross-validation. Best testing dataset is chosen on the basis of the fourfold cross-validation.

Table 2 Parameters setting of each optimization algorithm
Full size table

The considered input combinations are summed up in Table 3. The first three combinations (from i to iii) involve single inputs, second three combinations (from iv to vi) consider double inputs and the last combination (vii) tries all inputs for modeling dimensionless experimental discharge. Thus, all possible input combinations were considered in this study to determine the nest one for each implemented method.

Table 3 Input combinations used for model development
Full size table

The outcomes of the single ANFIS method are reported in Table 4 for training and testing stages of two types of pipes. It is seen from the table that h/D is more effective on DED than the other single inputs. H/D parameter causes the worst model efficiency, and involving this input combinations deteriorates the models’ performances. The best model was obtained with the inputs of h/D, w/D (combination iv) which produced the lowest RMSE (0.038 and 0.041), MAE (0.035 and 0.037) and the highest NSE (0.917 and 0.686), R2 (0.922 and 0.779) in modeling DED in pipe A and B, respectively.

Table 4 Results of the ANFIS models
Full size table

Tables 5 and 6 sum up the training and testing statistics of the hybrid ANFIS-PSO and ANFIS-GSA methods in modeling DED of two different pipes. Similar to the single ANFIS results, here also the h/D is the most effective input, while the H/D produces the worst accuracy. Among the all input combinations considered, the fourth one involving h/D and w/D has the best predictions. The best ANFIS-PSO has RMSE, MAE, NSE and R2 of 0.035, 0.032, 0.939 and 0.945 for pipe A, while the corresponding values are 0.036, 0.028, 0.805 and 0.819 in the testing stage, respectively (Table 5). The best ANFIS-GSA performed superior to the best ANFIS-PSO with lower RMSE (0.027 and 0.024), MAE (0.019 and 0.019) and higher NSE (0.969 and 0.846), R2 (0.973 and 0.968) in modeling DED of pipe A and B, respectively. Comparison of the single and hybrid ANFIS methods (Table 4, 5, 6) reveals that the PSO and GSA improve the accuracy of ANFIS in modeling DED of both pipes; improvements in RMSE are 7.89% and 28.95% for pipe A and 12.20% and 41.46% for pipe B by implementing the PSO and GSA, respectively.

Table 5 Results of the ANFIS-PSO models
Full size table
Table 6 Results of the ANFIS-GSA models
Full size table

The outcomes of the new ANFIS-PSOGSA method in modeling DED of two different pipes are given in Table 7. The effects of single inputs on DED are found similar to the single and hybrid ANFIS methods. Among the input parameters, the h/D is the most effective one with the lowest RMSE, MAE and the highest NSE and R2 in both pipes. Adding w/D to the h/D considerably improves the accuracy; RMSE and MAE of the testing stage decrease from 0.041 and 0.031 mm to 0.019 and 0.010 and NSE and R2 increase from 0.915 and 0.930 to 0.974 and 0.981 in pipe A, respectively. Comparison with the hybrid ANFIS-GSA and ANFIS-PSO reveals that the proposed ANFIS-PSOGSA performs better than the best ANFIS-PSO in modeling DED of pipe A and B, respectively. The ANFIS-PSOGSA respectively improves the accuracy of ANFIS, ANFIS-PSO and ANFIS-GSA by 50%, 45.71% and 29.63% for pipe A and by 68.29%, 63.89% and 45.83% for pipe B.

Table 7 Results of the ANFIS-PSOGSA models
Full size table

The testing performances of the ANFIS-based models are compared in Fig. 6 for pipe A in the form of scatterplot. As apparent from the graphs that the ANFIS-PSOGSA has the least scattered estimates while those of the single ANFIS seem to be the most scattered. The outcomes are evaluated on Taylor diagram in Fig. 7. The figure tells us that the new proposed model has the lowest RMSE and the highest correlation, and its standard deviation is closer to the observed one. It is evident from violin charts given in Fig. 8 that the ANFIS-PSOGSA model has the most similar distribution compared to other models, and the standard ANFIS model has the most inferior predictions. Similar outcomes were also obtained for pipe B, and they are plotted in Figs. 9, 10, 11 by scatterplot, Taylor and violin charts, respectively. These graphs also justify the better accuracy of the new ANFIS-PSOGSA in modeling DED compared to other alternative models.

Fig. 6
figure 6

Scatterplots of the observed and predicted dimensionless experimental discharge by different ANFIS-based models in the test period using best input combination—Pipe A

Full size image
Fig. 7
figure 7

Taylor diagrams of the predicted hydraulic conductivity by different ANFIS-based models in the test period using best input combination—Pipe A

Full size image
Fig. 8
figure 8

Violin charts of the predicted dimensionless experimental discharge by different ANFIS-based models in the test period using best input combination—Pipe A

Full size image
Fig. 9
figure 9

Scatterplots of the observed and predicted dimensionless experimental discharge by different ANFIS based models in the test period using best input combination—Pipe B

Full size image
Fig. 10
figure 10

Taylor diagrams of the predicted dimensionless experimental discharge by different ANFIS-based models in the test period using best input combination—Pipe B

Full size image
Fig. 11
figure 11

Violin charts of the predicted dimensionless experimental discharge by different ANFIS-based models in the test period using best input combination—Pipe B

Full size image

Discussion

The aim of the present study was to improve the accuracy of ANFIS method using PSOGSA metaheuristic algorithm to get better model for prediction of dimensionless experimental discharge. To understand this, the newly developed method was compared with hybrid ANFIS-PSO, ANFIS-GSA and standalone ANFIS. It was observed that the PSO and GSA considerably improve the ANFIS performance in modeling DED by decreasing RMSE by 7.89% and 28.95% for pipe A and by 12.20% and 41.46% for pipe B. Furthermore, the ANFIS-PSOGSA improves the accuracy of ANFIS-GSA, ANFIS-PSO and ANFIS by 29.63%, 45.71% and 50% for pipe A and by 45.83%, 63.89% and 68.29% and for pipe B, respectively.

It was observed from the outcomes of considered methods (see Table 4, 5, 6, 7) that h/D input parameter is more effective on DED compared to w/D and H/D. Combining two inputs h/D and w/D improves the accuracy and provided the best efficient model in all methods. It was observed that the models with input combination vi (h/D and H/D) performs superior to the model with input combination v (w/D and H/D) as expected because h/D was more effective on DED than the w/D. These results have an agreement with the previous studies (Parsaie et al. 2019; Parsaie and Haghiabi 2020). Parsaie et al. (2019) predicted discharge coefficient of combined weir–gate using ANN, ANFIS and SVM and according to the sensitivity analysis they found that the h/D is the most effective parameters. Parsaie and Haghiabi (2020) used GMDH, GEP and MARS methods for predicting discharge coefficient of combined weir–gate and they reported that the h/D as the most important parameter. According to the geometry of the experimental model used in the current research (Fig. 1), the flow through the weir–orifice is directly related to the upstream water depth (h). Moreover, the flow through the orifice depends on the orifice opening height (W). So, from a hydraulic point of view, the (h/D) and (W/D) variables can be identified having the highest influence on the discharge coefficient of the weir–orifice. However, in the last input combination (vii), the accuracy of the models decreased by involving all three input parameters. Normally, improvement in models’ accuracy is expected for this combination. As also reported by previous studies (Shi et al. 2012; Zhang et al. 2019), use of more inputs does not guarantee better prediction accuracy. More inputs may have a negative impact on variance and produces a more complicated model and this may lead poor prediction accuracy (Adnan et al. 2019). Hence, different combinations of inputs should be tried in such modeling issues as done in the presented study.

Parsaie et al. (2019) investigated the accuracy of ANN, ANFIS and SVM in predicting discharge coefficient of combined weir–gate and they obtained the best R2 accuracies for the ANN, ANFIS and SVM models as 0.91, 0.94 and 0.91, respectively. Parsaie and Haghiabi (2020) compared the GMDH, GEP and MARS methods for predicting discharge coefficient of combined weir–gate and they obtained the best accuracy from MARS which produced a R2 of 0.89. In the presented study, the PSOGSA provided the best accuracy by producing R2 of 0.981 and 0.902 for pipe A and pipe B, respectively. This indicates that the proposed method has an acceptable accuracy in predicting the dimensionless experimental discharge of combined weir–orifices.

The general outcomes of the presented study reveal the superiority of the PSOGSA algorithm in tuning ANFIS parameters compared to PSO and GSA in modeling DED. As can be understood from its name, the PSOGSA was developed by combining PSO and GSA. It integrates the capability of PSO exploitation and GSA exploration and thus it uses advantages of these two algorithms. The PSOGSA can be able to escape from local optimums with faster convergence compared to PSO and GSA (Mirjalili and Hashim 2010).

Concluding remarks

By this study, the performance of PSOGSA algorithm was investigated in tuning ANFIS parameters for modeling dimensionless experimental discharge of combined weir–orifices. ANFIS-PSOGSA model was compared with hybrid ANFIS-PSO, ANFIS-GSA and standard ANFIS models to evaluate viability of the proposed algorithm. Various combinations of dimensionless input parameters consisting h/D, w/D, H/D were tried using each method to estimate dimensionless experimental discharge. Among the input parameters, the h/D was found to be the most effective input on modeling dimensionless experimental discharge while involving the H/D parameter deteriorated the models’ performances. Comparison of the ANFIS-based models revealed that the metaheuristic algorithms considerably improved the standard ANFIS in modeling dimensionless experimental discharge. The PSOGSA provided the best accuracy and improved the accuracy of ANFIS-GSA, ANFIS-PSO and ANFIS by 29.63%, 45.71% and 50% for pipe A and by 45.83%, 63.89% and 68.29% for pipe B, respectively. This study recommends the employment of the PSOGSA which uses the synergy of two metaheuristic algorithms in modeling dimensionless experimental discharge.

The outcomes of this study have practical implications for the field of hydraulic modeling and prediction. The proposed ANFIS-PSOGSA model, leveraging the synergy of PSO and GSA, provides a reliable and accurate tool for dimensionless experimental discharge prediction. Engineers and researchers in the field of fluid dynamics and hydraulic engineering can benefit from the enhanced accuracy of this model, particularly in scenarios involving combined weir–orifices.

Future studies can compare this method with other advanced machine learning and deep learning methods. The generalization ability of the proposed method can be further investigated by applying more experimental data.