Introduction

Land surface exchanges energy and mass with the atmospheric boundary layer; therefore, it affects the weather; in return, climate alters the land surface through variations in moisture and heat generated by precipitation, radiation, and other factors (Wood et al. 1992; Betts et al. 1996; Dan et al. 2015; Ekwueme and Agunwamba 2021). Studies have shown that 64.73% of annual variation in runoff is due to climatic variables (Ekwueme and Agunwamba 2020). Therefore, models that can simulate these interactions are important for hydrologists, meteorologists, and related scientists. Land surface models (LSM) simulate bottom boundary conditions to be used in weather and climate models by solving the energy, water, and carbon balance. Due to population pressure and climate change, estimation of water resources availability is one of the most important aspects to be considered by water managers and land surface models can represent it (Overgaard et al. 2006).

The sketch of Noah LSM presented by Oregon State University (OSU) was developed in the 1980s at OSU (Mahrt and Pan 1984) and upgraded by the National Centers for Environmental Prediction (NCEP) (Chen et al. 1996). The multiparameterization options were added to the Noah model, and Noah-MP was produced (Niu et al. 2011). This model has different parameterization schemes, which are called “options,” for each physical process; therefore, it makes it possible to carry out different experiments by combining these schemes (Li et al. 2022). Noah-MP allows the user to form multi models produced by a grouping of parameterization schemes with new and more realistic options to simulate biophysical and hydrological events. This is the unique ability of the Noah-MP model (Niu et al. 2011; Hong et al. 2014; Zhang et al. 2016; Gan et al. 2019; Zhuo et al. 2019) compared to the other land surface models that help researchers to experiment with the different schemes for phenomena and simulate land surface more realistically (Chang et al. 2022). On a global scale, the results of the model can be compared to satellite data and observations (Yang et al. 2011; Pilotto et al. 2015; Ma et al. 2017). Noah-MP has shown significant progress in modeling hydrological parameters including soil moisture, runoff, groundwater, and ET (Cai et al. 2014a; Barlage et al. 2015; Zheng et al. 2017; Yang et al. 2019); in addition, the results indicate that the simulation of Noah-MP model can be greatly improved by assimilating input observations data such as leaf area index, snow cover fraction within hybrid methods (Zhao and Yang 2018; He et al. 2022).

In other studies of water management in watersheds, the hydrologic models were applied. The different data to develop these models have been collected for the small units of area (e.g., the hydrologic response unit in the SWAT model). Providing these distributed models for large watersheds or regional scales is expensive, time-consuming, and sometimes impossible (Saadatpour et al. 2019; Nasiri et al. 2020; Izady et al. 2022); therefore, the findings from an advanced land surface model with large pixel have inspired us to investigate for the first time whether this model could simulate the three important hydrological variables (runoff, soil moisture, and evapotranspiration) in the arid and semiarid watersheds in Iran with lack of measurements. Although the model outputs are usually reported for a large-scale area, the data to evaluate the results of the model were only available in the Neyshaboor watershed, and for ten years, it can be representative of most of Iran watersheds. Therefore, Neyshaboor watershed was selected. After assessing the Noah-MP model, if the model simulates the water balance components with acceptable accuracy, it can be used for estimating major hydrological parameters on a larger scale in Iran with a lack of observations. The model performed with its own assumptions.

GLDAS applies a set of land surface observations and satellite data, assimilation techniques, and land surface models to present land surface state (e.g., soil moisture and surface temperature) and flux (e.g., evaporation and sensible heat flux) parameters. GLDAS supplies land surface data at 2.5° to 1 km resolutions, and the temporal resolution is 3 h (Rodell et al. 2004; Fang et al. 2009; Chen et al. 2013; Yang et al. 2019). These products are presented for a variety of purposes, perhaps their most important application is to be the land model benchmarking (Van Den Hurk et al. 2011; Park and Park 2016). Although GLDAS drives four land surface models, the Noah model with multiparameterization options does not exist in this system. Examining Noah-MP’s output in a different region of the world and comparing it with observations is an effort to join the Global Benchmarking Project.

Zhang et al (2016) showed that the uncertainty in precipitation data exerts a greater impact on the Noah-MP simulations relative to the vegetation parameter (i.e., LAI) thus the precipitation data were corrected after comparing with observational data by their nonlinear method to evaluate the model more accurately. Additionally, to indicate the ability of the dynamic vegetation scheme in the Noah-MP model, evapotranspiration is divided into evaporation and transpiration components for the first time in this model.

In general, the ability of the model to provide acceptable results in the arid and semiarid regions was investigated. Sect. ”Materials and methods” describes the model and study area, introduces the observation and model input data, presents sensitivity analysis, calibration, spin up, and the evaluationn methods; Sect. ”Results and discussion” presents the evaluations of soil moisture, runoff, and ET and Sect. ”Conclusions” summarizes the model results and presents suggestions for future research.

Materials and methods

The Noah-MP model

Noah-MP is a progressive version of Noah LSM using multi-physics options to simulate flux exchange between the land surface and the atmosphere. Noah-MP has a separate vegetation canopy layer in comparison with Noah LSM; therefore, the upgraded model has a separate calculation for temperature, energy, and water component (Niu et al. 2011). Three layers of snow (Niu and Yang 2003) are added to the top of the soil column in Noah-MP which helps estimate correct albedo and available energy at every time step and also simulate the time of snowmelt correctly. The recent snow structure makes it possible to calculate phenomena in layers of snow, for example infiltration, conservation, and freezing water (Niu and Yang 2006).

The Noah model has free drainage at the lowest depth of 2 m soil column, which ignores the mechanism of soil–water interaction with groundwater. Noah-MP model includes a simple groundwater model (Niu and Yang 2007), which allows users to add drained water from soil column to groundwater or to apply groundwater for evaporative requirement in the warm seasons. There is a new scheme for frozen soil in Noah-MP that prevents low infiltration resulting in the production of large amounts of runoff on the surface compared to the existing scheme in Noah (Niu and Yang 2006). The Noah-MP model has other extensions: (1) the Ball–Berry scheme (Ball et al. 1987) is a type of stomatal resistance added to the model to simulate photosynthesis of the leaves growing in the shadow and the sun and (2) a dynamic vegetation model (Dickinson et al. 1998) that considers produced carbon in vegetation and soil separately. A semitile subgrid scheme and two-stream radiative transfer treatment (Yang and Friedl 2003; Niu and Yang 2004) are used in the model to omit excess shadows and to consider space between-canopy gaps. Noah-MP model has multi-physics options for each physical process which allows the modeler to do the experiment with a different set of schemes and evaluate the results (Yang et al. 2011). Soil water movement(θ) is modeled with the diffusivity form of Richards’ equation (Koren et al. 1999; Balsamo et al. 2009):

$$\frac{\partial \theta }{{\partial t}} = \frac{\partial }{\partial z}\left( {D\frac{\partial \theta }{{\partial z}}} \right) + \frac{\partial K}{{\partial z}} + S$$
(1)

where hydraulic conductivity (K (m/s)) and water diffusivity (D (m2/s)) are functions of soil texture and soil moisture content and S indicates water sources or sinks, increases soil moisture by infiltration, or decreases it by evaporation. SIMTOP is a simplified TOPMODEL and a proposed option by Noah-MP for the simulation of surface and subsurface runoff (Niu et al. 2011). Surface runoff (Rs) is produced when a grid cell is saturated as presented in the Eq. (2):

$$R_{{\text{s}}} = Q_{{{\text{wat}}}} \left( {\left( {1 - F_{{{\text{frz}}}} } \right)F_{{{\text{sat}}}} + F_{{{\text{frz}}}} } \right)$$
(2)

Qwat is the incident water on the soil surface. The saturated fraction (Fsat) is expressed as follows:

$$F_{{{\text{sat}}}} = (1 - F_{{{\text{frz}}}} )F_{\max } e^{{ - 0.5f(z_{\nabla } - z{\prime}_{{{\text{bot}}}} )}} + F_{{{\text{frz}}}}$$
(3)

where Ffrz is a fractional impermeable area that is a function of the ice content in the surface soil layer and Fmax–the potential or maximum saturated fraction of a model grid cell–is the portion of the accumulative area of subgrid cells that have a topographic index being equal to or larger than the grid cell mean topographic index. The topographic index in every grid cell can be obtained from high‐resolution subgrid topography (Niu and Yang 2006). f is the decay factor and can be determined through sensitivity analysis or calibration against the hydrograph recession curve and globally f = 6.0. z∇ is water table. Z′bot = 2 m is the depth of the model bottom. The base flow or subsurface runoff is represented as shown in Eq. (4):

$$R_{{{\text{sb}}}} = R_{{{\text{sb}},\max }} e^{{ - \Lambda - f(z_{\nabla } - z{\prime}_{{{\text{bot}}}} )}}$$
(4)

When the grid cell mean water table depth is zero, the maximum subsurface runoff (Rsb,max) has occurred and globally Rsb,max = 5.0 × 10−4 m/s obtained from sensitivity tests and calibration against global runoff data (Niu and Yang 2007). Plus, Λ is the grid cell mean topographic index, with a global mean value of Λ = 10.46 derived from HYDRO1K 1 km WI data. Total evapotranspiration is a sum of canopy evaporation, soil evaporation, and transpiration. Potential evapotranspiration is calculated using the Penman–Monteith equation (Zeppel 2011). Transpiration is achieved according to the state of the canopy. The transpiration conductance determines the state of the canopy and leaf to canopy air (ctw (m/s)), and this coefficient entered into the formula. The transpiration conductance (ctw) is determined based on sunlit and shaded leaf area index, leaf boundary layer resistance, sunlit, and shaded stomatal resistance. The values of ctw are strongly dependent on the period of plant growth. Therefore, the actual transpiration in the Noah-MP model varies with time by Eq. (5):

$$T_{{\text{r}}} = F_{{{\text{veg}}}} *\rho_{{{\text{air}}}} *C_{{\text{p}}} *C_{{{\text{tw}}}} *\left( {E_{{\text{s}}} \left( {T_{{\text{v}}} } \right) - E_{{{\text{ah}}}} } \right)/\gamma$$
(5)

where Tr is transpiration heat flux (w/m2), Fveg is greenness vegetation fraction (–), ρair is the air density (kg/m3), Cp (= 1004.64) is the heat capacity of the dry air at constant pressure (j/kg/K), Ctw is the transpiration conductance, leaf to canopy air (m/s), Es(Tv) is the saturation vapor pressure at Tv (pa), Eah is the canopy air vapor pressure (pa) and γ is the psychrometric constant (pa/K).

Study area

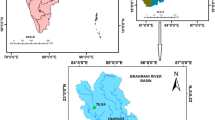
The study area is Neyshaboor watershed in the northeast of Iran that is located between 35°40′–36°39′ N and 58°17′–59°30′ E, with semiarid to arid climate (Fig. 1). The total geographical area is 9158 km2 which consists of 4917 km2 plain and 4241 km2 mountainous terrains. 29% of the total area is irrigated. The highest elevation of Neyshaboor changes from 3300 m in the mountains to 1050 m in the plain. The mean annual temperature of the watershed ranges between 13 and 13.8 °C. The average annual precipitation is 265 mm. The watershed was divided into three regions: mountain (grids: 1, 4, 8, 12), foothills (grids: 2, 3, 5, 9, 13, 14, 15), and lowland (grids: 6, 7, 10, 11) for two reasons: first, the importance of cell uniformity in terms of vegetation and soil texture and topography in calculating runoff using the SIMTOP method and, second, inaccessibility of the information of the smaller cells for this model.

Fig. 1
figure 1

Location of Neyshaboor watershed in Iran and grid cells

Full size image

Observation data and model input data

In this study, 0.25-degree spatial resolution used, 3‐hourly meteorological data provided by GLDAS-1 to run the Noah-MP model version 1.1 at hourly time step from 24 February 2000 to the end of 2009. GLDAS drives multiple land surface models uncoupled to an atmospheric model. In this research, the Noah LSM outputs were used. The data were (1) surface pressure, (2) near-surface air temperature, (3) near-surface wind speed, (4) near-surface specific humidity, (5) precipitation (snow and rainfall), (6) surface incident shortwave radiation, and (7) surface incident longwave radiation. There are many studies that the spatial and temporal variability of climatic parameters has investigated by statistical tools (Ekwueme and Agunwamba 2021). The precipitation data have been corrected by matching the mean and the coefficient of variation of GLDAS data with Meteorological Organization data. The bias-corrected precipitation data were done by the method proposed by Terink et al (2009). The difference in average daily precipitation between GLDAS1 data and observational data was in the range of 0.3–0.048 mm after this method effectively reached to 0.048 mm. The R-squared value between the coefficient of variation of GLDAS data with observational data improved from − 5.14 to 0.99 on the daily scale. The irrigation water has been added at the rate of 15–25 mm per month to the Noah-MP model precipitation. The initial conditions include soil moisture, soil temperature, skin temperature, canopy water, snow water equivalent, and deep soil temperature at the start of the simulation. They were provided by the output of the GLDAS-1/Noah data. Other initial conditions were selected from arbitrary values that are globally constant (Yang et al. 2011).

U.S. Geological Survey (USGS) 30-s global 24-category vegetation map and hybrid State Soil Geographic (STATSGO)/Food and Agriculture Organization (FAO) Five-minute 16-category soil texture map was the sources to acquire vegetation and soil type. There were local land use map and soil map at a scale of 1:100,000 in Khorasan Razavi Regional Water Authority that allocate various vegetation types to a grid; in accordance with the model structure, the dominant land use was considered as a representative of the whole of the grid which is not reality and probably reduces the accuracy of the simulation. As can be seen from Table 1, the global vegetation map predicts shrubland for the whole watershed, while the local map adds two other types of vegetation: mixed dryland/irrigated and mixed shrubland/grassland. Also, the global soil map represents clay loam and loamy sand for the grids but the local maps include two other texture: sandy loam and loam. Generally, local maps exhibit more varied vegetation and textures.

Table 1 Land use and soil type of grid cells accordance with global map and local map
Full size table

Soil moisture has been measured volumetrically on several days from May 2008 to June 2009 using a humidity meter (type TRIME-FM, Germany) in another local research. They have been performed in three replicates and days without irrigation. The measurement in two fields and two depths were pickup for model evaluation.

Sensitivity analysis, calibration, and spin up

Since the values of the initial parameters were selected from GLDAS, which are not far from reality, the first two years of implementation 2000–2001 were considered as the spin-up time. The model was run daily by the default options except for the vegetation model in which dynamic option was selected. Sensitivity analysis methods are carried out for a variety of reasons (Hamby 1994), but the main reason here is to determine the most critical parameters in the final runoff value in the watershed and to calibrate the model accordingly (Bastidas et al. 1999). The most popular and simple method of sensitivity analysis is to change a parameter, while the others are constant. The extent and sensitivity of the parameter can be captured by changing (for example, increasing) each parameter gradually and measuring its effect on the model output. This method has been known as a “local” analysis (Hamby 1994) and has been applied extensively for sensitivity analysis in other models (Pitman 1994; Wen-Yih Sun and Bosilovich 1996). Twenty-eight model parameters were examined that seemed to be more effective in the runoff and represented similar parameters. They were eleven soil and three vegetation parameters along with eight parameters extracted from the dynamic vegetation model and six parameters in the groundwater module. Table 2 displays the descriptions, units, and ranges of the parameters. The range of parameters was obtained from the default value in the manual, literature review (Rosero et al. 2010), and software of the soil science, and was then modified by the local information regarding the watershed.

Table 2 Descriptions of parameters used in the Noah-MP model, units, and ranges for calibration
Full size table

Calibration was performed based on sensitive parameters in the sensitivity analysis. The fifteen rain gauges were located in seven grid cells, and nine hydrometric gauges were located in four grid cells. The impassable heights could be a reason for the few gauges. The measurements were not captured, in some years. The human activities in this watershed (e.g., artificial groundwater recharge sites and the dam construction close to gauges) may reduce the accuracy of hydrologic data; therefore, simulated runoff from the SWAT model was used for sensitivity analysis and calibration. The SWAT model has been already calibrated (the R2 and NSE for simulated runoff were obtained 0.77 and 0.74, respectively) using a combination of hydrometric gages and historical crop yield data to improvement the uncertainty of outputs (Izady et al. 2015). The runoff of each grid cell was calculated by the area-weighted average of runoff among sub-basins of the SWAT model placed in the same grid and was then compared to the equivalent value in the Noah-MP model, and the parameters were optimized. The samples of model parameter sets were obtained by Latin hypercube sampling (LHS). LHS is a stratified random method with only one sample in each row and each column in a multi square grid (Minasny and McBratney 2006).

Evaluation statistics

In order to evaluate the model results, runoff and evapotranspiration values were extracted from the model and then compared with SWAT outputs by three indexes: root-mean-square error (RMSE), the square of the correlation coefficient (R2) (Santhi et al. 2001; Liew et al. 2003), and Nash–Sutcliffe efficiency coefficient (NSE) (Niu and Yang 2006; Moriasi et al. 2007). Lower RMSE values and R2 and NSE values greater than 0.5 show encouraging performance.

Results and discussion

Sensitive parameters

RMSE between the reference and modeled runoff was estimated for the sample range in order to discover runoff sensitivity to Noah-MP model parameters (Jhorar et al. 2002). The Clapp–Hornberger “b” parameter (b (–)), saturated soil hydraulic diffusivity (satdw (–)), porosity (maxsmc (m3/m3)), maximum saturated fraction (fsatmx (–)), specific leaf area (sla (m2/m2)), micropore content (cmic (–)), runoff decay factor (f (1/m)) were identified as the most sensitive to the least sensitive, respectively. The climatic conditions of the watershed affect the initial value of parameters and the determination of sensitive parameters (Rosero et al. 2010). In some regions, runoff simulation is extremely sensitive to three parameters: the surface dryness factor (α), the saturated hydraulic conductivity (satdk), and the saturated soil moisture (θmax) (Cai et al. 2014a).

The results of the sensitivity of runoff to Noah-MP model parameters are shown in Fig. 2. In Fig. 2, the greater slope of RMSE indicates the greater sensitivity of the runoff to the parameter. This method visibly shows the runoff error created by parameter changes and, moreover, indicates the appropriate parameter range for calibration. The calibration of the model started with this seven parameters. The final range of sensitive parameters after calibration is given in Table 3. The runoff had the most sensitivity to the saturated soil hydraulic diffusivity and Clapp–Hornberger “b” parameter and the least sensitivity to the runoff decay factor “f.”

Fig. 2
figure 2

The RMSE of the simulated runoff as a function of the Noah-MP model parameters

Full size image
Table 3 Final parameter ranges (minimum and maximum) and units
Full size table

Runoff

Figure 3 shows Noah-MP simulated monthly runoff, SWAT simulated monthly runoff, and precipitation in three regions from January 2002 to December 2009. Figure 3 shows the monthly modeled Noah-MP runoff generally follows the variability of the precipitation. According to Table 4, the best simulations belong to the mountain, lowland, and foothills, respectively. The Noah-MP model cannot simulate agriculture and irrigation in lowlands, and this is one of the reasons that the Nash coefficient of runoff is lower than in the mountain. Since the hydraulic characteristics of the plain have been affected by human activity and these changes cannot completely be considered in the large grids of the Noah-MP model, values of NSE and RMSE reduce. The minimum value of this coefficient belongs to the foothills because each cell in this region is a combination of elevations and lowlands, and considering one type of vegetation and soil texture for the whole cell has created this issue. In another research, the Noah-MP presented a better runoff simulation but a worse ability in simulating evapotranspiration over most regions in comparison with FLUXNET tower observations. This research suggested improving the dynamic vegetation model, lake water storage dynamics, and human activities including irrigation (Ma et al. 2017)

Fig. 3
figure 3

Simulated monthly runoff by Noah-MP and SWAT model and sum of irrigation and precipitation in a mountain, b lowland, and c foothills

Full size image
Table 4 Model evaluation after calibration
Full size table

Evapotranspiration

The simulated monthly mean evapotranspiration of Noah-MP and SWAT models is shown in Fig. 4. As can be seen, the models show less evapotranspiration in autumn and winter and more evapotranspiration in spring and summer due to warmer climate with different temporal patterns. For better comparison, the simulated monthly mean evapotranspiration and its components over the last ten years are plotted in Fig. 5. The soil evaporation, transpiration, and canopy evaporation were calculated to be 156, 117, and 33 mm, respectively.

Fig. 4
figure 4

Noah-MP and SWAT simulated monthly ET

Full size image
Fig. 5
figure 5

SWAT and Noah-MP simulated mean monthly evapotranspiration and Noah-MP’s components (soil evaporation, canopy evaporation, transpiration)

Full size image

Figure 5 shows that the mean evapotranspiration of the Noah-MP model is higher than in the SWAT model in May, June, and July, and it is lower in November, January, February, and March. SWAT model shows the peak of evapotranspiration in April, whereas the highest evapotranspiration in the Noah-MP model is observed in May. As shown in Fig. 5, the evaporation pattern in the Noah-MP model is similar to the SWAT model, but the transpiration is different. As the weather warms up and the radiation increases, transpiration increases and reaches its maximum in June and decreases in colder months. This seems to be due to plant activity throughout the year, and the dynamic vegetation model has created this pattern by simulating plant growth. The amount of transpiration is added to the amount of evaporation from the soil, which increases its value and changes the evapotranspiration pattern. As can be seen in Fig. 5, evapotranspiration during cold months of the year, especially in December and January, is lower than the SWAT model. Apart from the dependence of evaporation on model parameterization, due to the dependence of evaporation on meteorological variables, we should look for the reasons of this underestimation in the deviation of input data. As noted in this study, precipitation data have been corrected, but no corrective data have been available for other meteorological data, although attempts have been made to increase the GLDAS input data, which were estimated to be low in the watershed. Another reason for under is related to the lack of human activities in the Noah-MP model. Accordingly, after the warm months, the vegetation model considers the end of the growing season and the lowest leaf area index for the plant; thus, it calculates the transpiration at zero or near zero in the cold months while winter cultivation and transpiration of plants continue in Neyshaboor watershed. Also, cultivation in the plain and regular irrigation throughout the year, which is not simulated by the Noah-MP model, can change the pattern.

The annual evapotranspiration of the two models is also shown in Fig. 6. The estimated annual evapotranspiration value of the model is close to the estimated value of the SWAT model. The two models are close to the average annual evapotranspiration rate of the Neyshaboor watershed approximately 300 mm (Mianabadi et al. 2016), and the Noah-MP model has an acceptable annual value.

Fig. 6
figure 6

SWAT and Noah-MP simulated annual evapotranspiration

Full size image

Soil moisture

The simulated soil moisture in grid cells 6 and 7 have been compared to observational data in Motamedieh and Faroob fields in the same cells in plain region. As shown in Fig. 7, the model was able to predict the pattern of observations.

Fig. 7
figure 7

Noah-MP simulated and field-observed daily soil moisture. a 0–10 cm Motamedieh field, b 10–40 cm Motamedieh field, c 0–10 cm Faroob field, and d 10–40 cm Faroob field

Full size image

In both grid cells, the coefficient of determination of the first layer (0–10 cm) is larger than the second layer (10–40 cm). This is probably due to the fact that in Noah-MP model only the specifications of the first layer of soil are determined according to the land surface, and same specifications are considered for other layers, which is one of the weaknesses of this model.

The highest matching at both depths was observed in both fields during rainiest seasons, namely autumn, winter, and early spring. As shown in these graphs, the model generally underestimated soil moisture in the warm months of April, May, July, and August due to evapotranspiration values. During these months, the evapotranspiration is overestimated according to the results obtained in the evapotranspiration section. In fact, due to high values of simulated evapotranspiration, the soil loses more water, which results in less moisture in the simulated soil compared to the observations. In similar research, Noah-MP has moderate improvements in modeling evapotranspiration and soil moisture and the Noah-MP has the best performance among other land surface models (Cai et al. 2014b).

The limitations of this study are as follows: There were not sufficient data about the watershed. Thus, the model was executed with large grid cells (in comparison with the watershed area) caused a reduction in model efficiency, probably. As mentioned earlier (2.4), the shortage of observational data in the whole of the watershed, induced simulated runoff and evapotranspiration to be compared with the SWAT outputs, and the simulated soil moisture evaluate with measured data in only two cells. The model could not simulate human activities on farms. The strength of this study was the correction of precipitation before using it for the model. The Noah-MP model evaluation criteria after calibration did not have improvement; therefore, this watershed does not require calibration because this model has a physical basis. The simulation of Noah-MP could be improved with inclusion or modification of additional processes such as lateral terrestrial water flow, evapotranspiration, and crop models (Yu et al. 2022; Meng et al. 2023; Sofokleous et al. 2023;).

Conclusions

In order to evaluate Noah-MP model, this model was executed in the Neyshaboor watershed with an arid and semiarid climate with the available water balance information. First, the model spin-up and sensitivity analysis were done, and then the model calibration and evaluation with SWAT model outputs were done simultaneously. Several conclusions from this study are as follows:

Based on the results of sensitivity analysis, runoff has the highest sensitivity to these parameters: the Clapp-Hornberger “b” parameter, saturated soil hydraulic diffusivity, porosity, maximum saturated fraction, specific leaf area, micropore content, and runoff decay factor.

Noah-MP-simulated runoff fits well with the SWAT model runoff. The best simulation belonged to mountainous areas because of its natural and intact essence with no human intervention (R2 = 0.78, NSE = 0.62, RMSE = 1.98 m3/s). Lowland ranked second in this simulation because Noah model lacks an option to simulate agriculture and irrigation. The third was the foothills because of the variations in topography and land use in each grid.

The Noah-MP estimated annual evapotranspiration close to the long-term average annual one (approximately 300 mm). The monthly evapotranspiration estimated by the Noah-MP model is different from the SWAT model, due to the fact that it does not modify all the forcing data and also Noah-MP does not take agriculture into account. Moreover, there is a dynamic vegetation model in Noah-MP that causes variations of evapotranspiration dynamically.

Noah-MP model could simulate soil moisture in the first and second layers in two grid cells in the plain (grid cells 6 and 7). The simulated soil moisture in the first layer (e.g., R2 = 0.62, RMSE = 0.059 m3/m3 in the Motamedieh field) is better than the second one (e.g., R2 = 0.57, RMSE = 0.052 m3/m3 in the Motamedieh field). The simulated soil moisture in rainy seasons is closer to observation because, in warm months, the evapotranspiration was overestimated; thus, soil moisture was underestimated. Since the model is provided with several options for runoff simulation, it is suggested that other model options be considered separately or a combination of them to calculate runoff in the arid and semiarid watersheds.

In this study, a specific configuration of options (referred to in Sect. ”Sensitivity Analysis, Calibration, and Spin up”) was selected. Although the results were acceptable, it is recommended that the model’s performance be evaluated with other configuration, and the role of irrigation in large agricultural regions added to the model. In future studies, the schemes for modeling the runoff can be compared to find the best scheme in every region.