Introduction

Groundwater is part of the water cycle located beneath the earth’s surface in pores and crevices of rocks and soil, the location present challenges for quantifying and management groundwater resources compared with surface water. The number of pores and crevices in the subsurface soil and rocks and their interconnectivity controls ease of movement of groundwater through the subsurface (Asfahani et al. 2023). In the coastal region where the depth to the water table is not very deep, vulnerability of groundwater to surface flow can be created as a potential risk to the groundwater resources. The knowledge of geohydraulic parameters can provide useful information that help in abstraction and management of the coastal groundwater resources (Ikpe et al. 2022). Geohydraulic parameters such as porosity, transmissivity, and hydraulic conductivity are important parameters in groundwater exploration and exploitation and as such there is need for prior knowledge of the subsurface hydro-geological conditions before drilling of a borehole/well (Ekanem et al. 2020, 2022a, b). It has been difficult to convince individuals especially in the coastal region to undertake geophysical survey before drilling and the refusal by some people to use the available geophysical report in areas that have been surveyed (George et al. 2022). This has resulted in incessant wildcat drilling and failed boreholes (Ibuot et al. 2013; George et al. 2014, 2021; Asfahani et al. 2023). Acquisition and interpretation of resistivity data have provided information about the subsurface geologic strata and the characteristics of the earth materials (George et al. 2015a, b; Lashkaripour and Nakhaei 2005; Niwas and Singhal 1981; Obiora et al. 2015; Ezema et al. 2020; Elemile et al. 2020a). A good understanding of the aquifer properties is essential in groundwater exploration as it helps in determination of the depth to the hydrogeologic units, groundwater flow and quality of the groundwater resources (Fitts 2002). Groundwater is that water that occurs in the pore spaces under the ground surface and in fractures of rock formations. The water produced is stored in a lithologic formation called aquifer.

Aquifer properties such as permeability, porosity, resistivity, layer thickness and aquifer yield control groundwater flow, availability, quality and potential (Uwa et al. 2018; George 2020). The aquifer hydraulic parameters can be estimated from the measured field parameters. These parameters vary spatially due to heterogeneity of the geology of an area (Ekanem et al. 2019; Elemile et al. 2020b). The soil and rock types affect the hydrophysical property of a formation; as such the absolute value of resistivity may not directly reflect it. In hydro-geophysics, the relationship between hydraulic conductivity which characterises the ease with which water flows in the subsurface and electric resistivity is important (Khalil and Santos 2009; Teikeu et al. 2012). Estimating hydraulic conductivity using resistivity measurements helps in the evaluation of groundwater potential; understanding the hydraulic response of the subsurface aquifer and estimating other hydraulic parameters. The variation of resistivity in the subsurface is caused partly by the seepage/leakage of fluid (water) from the surface and the resistivity response, which depends on the flow of the leaked fluid.

Surficial electrical resistivity measurement employing vertical electrical sounding is a nonintrusive technique, which is important in a geophysical survey to investigate the subsurface hydrogeologic units. The study area is devoid of adequate geohydraulic properties and since this wells drilling is done only with reference to the depth of the pre-existing wells. This practice, which leads to inadequate inventory of groundwater parameters, deprived the area of efficient exploitation, monitoring and management of groundwater resources (George et al. 2021). Many wells are abandoned due to poor quality water, while some of the functional ones are only used for washing of clothes and not for drinking. On the basis of this observation, this study was designed with the aim to estimate the geohydraulic parameters in order to appraise the groundwater repositories of the study area. It establishes the relationships between geohydraulic and geoelectric parameters such as hydraulic conductivity, transmissivity, transverse resistance and longitudinal conductance, which are paramount in determining potentiality of groundwater and groundwater vulnerability as well as quality. This paper employs the electrical resistivity data to estimate the geohydraulic properties of the subsurface aquifer units, and to establish the relationships between these parameters in order to improve its characterisation, which will enhance the determination of the aquifer potential and management of groundwater in the Littoral hydro-lithofacies in Uyo, Southern Nigeria.

Description of the study area

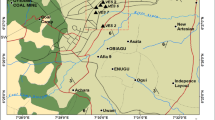
The study area, which is given in Fig. 1, is situated between the latitude 5.03°and 5.09°N and the longitude 7.41° and 8.10°E in the southern part of Nigeria and located in the equatorial climatic region characterised by two principal seasons which are the dry (November to February) and the wet (March to October) seasons. The relief of the study area according to Ugbaja and Edet (2004) is low with elevations of less than 10–50 m above sea level. The area is severely affected by the current global climatic changes, which lead to shifts in both the upper and lower boundaries of the climatic conditions (George et al. 2015a, b; Ibuot et al. 2017).

Fig. 1
figure 1

a Geologic map of Akwa Ibom State in Nigeria showing Uyo. b Map of Uyo Local Government Area showing VES points

Full size image

It forms part of the Cenozoic wave dominated Niger Delta region of Nigeria. According to Offodile (1992), the study area belongs to the deltaic marine environment of Cretaceous to recent age of which the Benin Formation is part. The Benin Formation which overlies the parallic Agbada Formation is of Tertiary to Quaternary Coastal Plain Sands. The Benin Formation is composed of interfringing units of lacustrine and loose fluvial sands, clays and lignite, pebbles, and layers of varying thicknesses which are classified as clastic sediments (Reijers et al. 1997). The thin lateritic overburden materials of varying thicknesses enclosed the Benin Formation at some locations, and this is massively exposed near the shorelines.

The major hydrological repositories of the area are controlled by permeability and porosity which are principal factors in determining the water-bearing potential of the area. This is characterised by uneven spread of thicknesses across the area forming systems of multiple aquifers flowing southward towards the Atlantic Ocean (Edet and Worden 2009), with the economic depths for groundwater cutting across arenaceous materials. The subsurface (boreholes) and surface (streams) are the major water sources that the inhabitants of the area depend on.

Theoretical background

The exploration for groundwater is affected by inadequate knowledge of the hydraulic properties of the subsurface aquifer. These properties play major role in the quantification of the subsurface hydrogeological units (George et al. 2015a, b). Hydraulic conductivity (K) is a property that characterises the hydraulic behaviour of an aquiferous layer and control the ease with which groundwater flow through an aquifer. It depends on the pore dynamics of the geomaterials the fluid is flowing through. The value of K is significant as it can be used as tools for hydrogeological modelling. In estimating the hydraulic conductivity, Eq. 1 (Kozeny–Carman–Bear’s model equation) was employed. Hydraulic conductivity, porosity and other site-dependent parameters are related by Eq. 1.

$$ K = \left( {\frac{{\delta _{w} .g}}{{\mu _{d} }}} \right).\left( {\frac{{d_{m} ^{2} }}{{180}}} \right).\left( {\frac{{\phi ^{3} }}{{\left( {1 - \phi } \right)^{2} }}} \right) $$
(1)

where \(\delta_{w}\) is density of water (1000 \({\text{kg/m}}^{{3}}\)), \(d_{m}\) is the mean grain size determined by direct measurement using vernier calliper and micrometre screw gauge as 0.00035 m, \(\mu_{d}\) is the dynamic viscosity of water given as 0.0014 kg/ms (Fetters 1994) and g is the acceleration due to gravity.

Aquifer formation factor (F) is a function of the porosity, pore structure, and pore size distribution of the aquifer units and is defined as the ratio bulk resistivity to that of water resistivity expressed in Eq. 2, where \(\rho_{b}\) and \(\rho_{w}\) represent the bulk aquifer and water resistivity, respectively. The electrical current flow through a formation is influenced aquifer properties such porosity (ϕ), pore shape and diagenetic cementation which according to Archie’s equation is expressed in the formation factor as given by Eq. 3 (Archie 1942).

$$ F = \frac{{\rho_{b} }}{{\rho_{w} }} $$
(2)
$$ F = a.\phi^{ - m} $$
(3)

where a is the pore geometry factor, and m is the cementation factor with their average values given as 0.5245 and 1.5431, respectively. According to Ransom 1984, the geometry pores, the compaction, isolating properties of cementation and mineral composition are some of the factors influencing m. The factor a indicates the influence of mineral grains on current flow and takes into account the contribution of mineral grains to electrical conductivity. Equation 3 gives the aquifer fractional porosity, and according to George et al. (2017), porosity and permeability are rocks properties that determine aquifer productivity. Tortuosity (\(\tau\)) which is the ratio of the actual distance travelled by the fluid through the porous media to the macroscopic length was estimated using Eq. 4. Tortuosity makes groundwater molecules and the contaminants that they may carry to move differently within the aquifer porous medium (Umoh et al. 2022). This aquifer property is controlled by porosity, pore shape and the shape of channels that connects the pores spaces.

$$ \tau = \left( {F\phi } \right)^{{\frac{1}{2}}} $$
(4)

Transmissivity (\({\text{Tr}}\)) determines the flow rate of groundwater through a saturated aquifer layer under a hydraulic gradient. The relationship between transmissivity and Dar-Zarrouk parameters according to Niwas and Singhal (1981) is expressed in Eq. 5. The product of the estimated K values and the aquifer thickness (h) gives the values of transmissivity (Eq. 5).

$$ {\text{Tr = }}K\sigma T = \frac{{KS}}{\sigma } = Kh $$
(5)

where S and T are the longitudinal conductance and transverse resistance, respectively, and are calculated using Eqs. 6 and 7 (Henriet 1976). The longitudinal conductance (S) is a measure of rock layer impermeability and it defines the degree of susceptibility to contamination. The transverse resistance (T) is proportional to the resistivity (ρ) and thickness (h) of the aquifer and shows the most favourable zones for hydrogeological exploitation.

$$ S = \frac{h}{\rho } $$
(6)
$$ T = h\rho $$
(7)

where h and \(\rho\) are the values of aquifer thickness and resistivity, respectively.

The product of aquifer conductivity and estimated hydraulic conductivity gives the values of K \(\sigma\). In locations with similar geologic setting and water quality, K \(\sigma\) is assumed to remain fairly constant (Niwas and Singhal 1981; Onuoha and Mbazi 1988; George et al. 2011).

Methodology

The electrical resistivity survey is aimed at assessing the subsurface resistivity distribution through measurements on the earth surface. The electrical resistivity method was adopted in this study to appraise the geohydraulic response properties of the aquifer units located within the mapped area of Fig. 1a, which lies between the latitude 5.03° and 5.09°N and the longitude 7.41° and 8.10°E in the southern part of Nigeria. Profiles for the study were taken along fairly straight traverses. The total traverse length for each sounding gives the maximum current electrode separation for that particular sounding. The study employed Schlumberger electrode configuration, which used vertical electrical sounding (VES) technique to acquire VES data in ten locations with the aid of IGIS Resistivity metre, model SSR-MP-ATS. The half current electrodes spread \(\left( \frac{AB}{2} \right)\) and half potential electrodes spread \(\left( \frac{MN}{2} \right)\) ranged from 1.0 to 400.0 m and 0.25–20.0 m, respectively. The resistivity metre measured the potential difference generated in the subsurface, and the process was repeated by increasing the spacing of the current electrodes proportionally from the midpoint point. Increase in spacing between the potential electrodes was done with care to ensure that the potential field was not weak and this was achieved by making sure the distance between the potential electrodes did not surpass one-fifth of the distance between the current electrodes (Obianwu et al. 2011a, b). As precautions, the profile lines were maintained at straight line and readings were not taken under the electric cables to avoid stray electromagnetic signals, which may affect the data (Inim et al. 2020; Ikpe et al. 2022). The data were manually smoothened to remove the outliers at the crossover distance, which were not consistent with the geology of the study locations (George et al. 2020). Although the interpretation of the acquired data was constrained by ground truth information, the resulting data were statistically found to be line with the data of similar geology within and outside the study area.

Practically, the apparent resistivity values (\(\rho_{a}\)) were calculated using Eq. 8:

$$ \rho_{a} = G\frac{V}{I} = G.R_{a} $$
(8)

where G is the geometric factor which depends on the electrode’s arrangements. \(R_{a}\) is the apparent resistance measured on the field. G is expressed in the relation below;

$$ G = \pi .\left[ {\frac{{\left( \frac{AB}{2} \right)^{2} - \left( \frac{MN}{2} \right)^{2} }}{MN}} \right] $$

The data were reduced to 1-D geological models utilising the manual and computer modelling techniques (Zohdy 1965; Zohdy et al. 1974). The computed apparent resistivities were plotted against \(\frac{AB}{2}\) on bi-logarithmic graphs, and the curves obtained were smoothened in order to eliminate the effects of lateral heterogeneities and other forms of noisy signatures (Chakravarthi et al. 2007; Akpan et al. 2006). The curves were curve matched using master curves and charts according to Orellana and Mooney (1966). The values of the apparent resistivity were inputted into computer software programme (WinResist) for the computer modelling which generates a set of geoelectric curves (Figs. 2, 3) from where the values of resistivity, thickness and depth of each geoelectric layer were obtained. The depths during the inversion process were constrained using borehole lithologic log by fixing layer thicknesses and depths while allowing the resistivities to vary (Batayneh 2009). This reduced the ambiguities in the interpretation stage and enhanced the reliability and quality assurance of the modelled results. The curves obtained from VES 3 and 9 showed good correlations between the borehole lithology log (Fig. 4) and the inverted results over half space. The curves show a wide variation in values of resistivity, thicknesses and depths between and within the subsurface layers penetrated by current.

Fig. 2
figure 2

Geoelectric curve at VES 3 and its parameters

Full size image
Fig. 3
figure 3

Geoelectric curve for VES 9 and its parameters

Full size image
Fig. 4
figure 4

VES lithology log with nearby boreholes

Full size image

Results and discussion

The results of VES interpretation show the variations in values of the bulk aquifer resistivity and thickness as a result of changes in physical and chemical properties of the subsurface earth materials as displayed in Table 1. The aquifer bulk resistivity (\(\rho_{b}\)) and thickness (h) were observed to range from 23.4 to 1306.2 Ωm and 7.4–56.3 m with their mean values of 347.99 ± 384.9 Ωm) and 35.39 m ± 13.6 m, respectively, while the water resistivity (\(\rho_{w} )\) ranges from 9.7 to 104.3 Ωm with an average of 38.94 ± 30.5 Ωm. The observed variation in resistivity of the aquifer layer can be influenced by the nature of the subsurface geomaterials and the continuous bioturbating activities (Thomas et al. 2020; Ekanem et al. 2022a).The aquifer geohydraulic parameters were estimated using the combinations of primary geoelectric parameters (aquifer resistivity, thickness and water resistivity) of aquifers; these parameters include aquifer formation factor (F), porosity (ϕ), tortuosity (τ), hydraulic conductivity (K), Dar-Zarrouk parameters [transverse resistance (T) and longitudinal conductance (S)] as shown in Table 1.

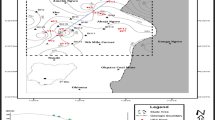
Table 1 Summary of estimated aquifer geohydraulic parameters
Full size table

The contour maps (Figs. 5 and 6) show the variation of aquifer resistivity and water resistivity; the variation of these parameters shows related trends with high resistivity in the north-eastern part of the study area. The zone with high aquifer resistivity is likely to have economical water repositories as they are probable going to be saturated with pore water.

Fig. 5
figure 5

Contour map of distribution aquifer bulk resistivity

Full size image
Fig. 6
figure 6

Contour map of distribution of water resistivity

Full size image

If the water is not exposed to surface contamination, clean groundwater could be accessed in the zones with higher resistivity. The low to moderate values spread across the southern part of the study area may be due to high clay or iron content (Uwa et al. 2018). The variations in Figs. 5 and 6 may be attributed to geological formations and divides (Mbonu et al. 1991 and Mauro et al. 2014). Figure 7 which is a plot of water resistivity against bulk aquifer resistivity gives a linear relationship with a diagnostic equation and a correlation coefficient (R2 = 0.941) given in Eq. 9. The scatter points observed in the plot is due to the heterogeneous nature of the geologic formation in the study area. This disparity in the formation is responsible for uneven waterborne susceptibility of the formation to weathering and erosion at the shorelines where these geologic units are exposed.

$$ \rho_{{{\text{w}} }} = 0.0{77}\rho_{{\text{b}}} + {12}.{12} $$
(9)
Fig. 7
figure 7

A graph of water resistivity against bulk resistivity

Full size image

The aquifer formation resistivity factor (F) for each point was computed using Eq. 2. The calculated values of F ranged from 2.41 to 12.52 with an average of 7.43, Fig. 8 shows the distribution of formation factor across the study area, and high formation factor is observed in the northern parts and decreases towards the south. The fractional porosity computed ranged from 0.20 to 0.46 with an average value of 0.28. This indicates that the aquifer layer is composed of fine-coarse grain sand. The distribution of porosity (Fig. 9) shows a reverse trend to that of formation factor and this agrees with Archie’s law that increase in porosity leads to decrease in formation factor. According to Mazac et al. (1985), grain size has no effect on porosity in uniform-sized sediments, but porosity varies only with the packing organisations of the grains and can also reduce as grain size increases (Mazac et al. 1985). A plot of formation factor (F) against fractional porosity (ϕ) (Fig. 10) gives a power expression as shown in Eq. 10 and shows inverse relationship between porosity and formation factor. This may be due to the high argillite–sand mixing ratio which reduces pore–matrix ratios in aquifers.

$$ F = 0.498\phi^{ - 2.00} $$
(10)
Fig. 8
figure 8

Contour map of aquifer formation factor

Full size image
Fig. 9
figure 9

Contour map of aquifer porosity distribution

Full size image
Fig. 10
figure 10

A graph of fractional porosity against formation factor

Full size image

Comparing Eq. 10 with Eq. 3, we can deduce the cementation factor (m) and the pore geometry factor (a) as 2.0 and 0.498, respectively.

The values of hydraulic conductivity (K) vary widely across the study area as displayed in the contour map (Fig. 11). The distribution of K shows high values in the southern part of the study area; this zone with high hydraulic conductivity zone corresponds to zone having high porosity and low resistivity. This agrees with literatures that hydraulic conductivity and electrical resistivity have inverse relationship (George et al. 2015b; Ibuot et al. 2019; Daniel et al. 2022). According to Vázquez-Báez et al. (2019), relatively high hydraulic conductivity indicates the ease of transmissibility of fluid, while relatively moderate and low values indicate a gradual measure of the declining rate of transmission of fluid within the aquifer system in the study area.

Fig. 11
figure 11

Contour map showing the distribution of hydraulic conductivity

Full size image

The values of tortuosity range from 1.09 to 1.58; in Fig. 12, high tortuosity is observed across the northern part of the study area with low values observed in the southern parts. This implies that tortuosity increases as formation factor increases (Fig. 8).This implies that argillites present in the fine-coarse sequence of sands hinder the rate of flow of water when comparing the macroscopic flow path length between the water/fluid inlet and outlet (George et al. 2015a; Ibanga and George 2016).The aquifer is also characterised by transmissivity ranging from 0.001 to 0.037m2/s averaging about 0.010037m2/s (0.010520 m2/s). Figure 13 shows the spatial variation of transmissivity across the study area, and it increases towards the southern part of the study area corresponding to zone with low resistivity and high hydraulic conductivity. This indicates good communication pore channels, high groundwater potential and the presence of materials that are highly permeable to fluid movement (Obiora et al. 2015). The high transmissivity values indicate high transmissivity magnitude, thus reflecting prolific aquifer repositories (Krasny 1993).

Fig. 12
figure 12

Contour showing the variation of tortuosity

Full size image
Fig. 13
figure 13

Contour map showing the distribution of transmissivity

Full size image

The contour map (Fig. 14) displays the variation of the longitudinal conductance and the map shows that the eastern part has low protective capacity, and on the average the area may be classified as been slightly vulnerable to contamination from surface contaminants. The values of longitudinal conductance represent poor to moderate protection (Oladapo et al. 2004).

Fig. 14
figure 14

Contour map showing the variation of longitude conductance

Full size image

The values of the transverse resistance (T) range from 549. 9 to 69097 Ωm2, the contour map (Fig. 15) shows the variation of T where the high values are observed in the northeastern part corresponding to zone with high aquifer resistivity, and this correlates well with resistivity as shown in Figs. 5 and 15. The observed high values of T indicate prolific and well-exploited aquifer repositories but prone to surface contamination due to low longitudinal conductance (Obiora et al. 2015).

Fig. 15
figure 15

Contour map showing the variation of transverse resistance

Full size image

Conclusion

This paper demonstrates the importance of using the VES data in characterising the aquifer repositories in terms of geohydraulic parameters and also establishes relationships between aquifer geoelectric and geohydraulic parameters. The results from the study delineate the aquifer units to be unconfined and show wide variations of the measured and estimated geohydraulic parameters across the study area as a result of inhomogeneity of arenaceous geological water repositories. The results revealed that the northeastern part of the study area has high bulk aquifer and water resistivity, while porosity, transmissivity and hydraulic conductivity are high in the southern part of the study area and demonstrate the study area as having prolific aquifer repositories. The quantitative estimated parameters proved significant and helpful in understanding the geohydraulic response of the subsurface aquifer and enhance a better understanding of the geohydrodynamics of study area. The spatial variation of these parameters will be useful in the management and sustainability of groundwater resources. The estimated geohydraulic response parameters will be useful in selecting the matching pump for water boreholes in the study area.