Introduction

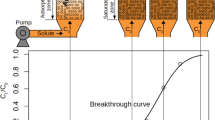
One of the most critical issues of this century is environmental pollution due to advances in modern industrial practices. Heavy metal ions are distinct from other harmful pollutants by their inability to biodegrade, resulting in significant physiological and neurological damage to human beings and aquatic life. Precipitation, oxidation/reduction, ion exchange and adsorption are some of the methods of metal ion remediation. Each of these techniques has a number of advantages and disadvantages; however, adsorption results in high-quality treated water at a low cost (Lakshmipathy and Sarada 2015). It also offers a simple design and fast operation (Arbabi and Golshani 2016). Evaluation of fixed-bed columns for the industrial pollution abatement has drawn the attention of scientists. A fixed-bed column is an effective option for the cyclic adsorption/desorption (adsorption hysteresis) in the industrial applications as it makes the best use of concentration and pressure gradient which are driving forces in adsorption (Hefti et al. 2015). One of the advantages of a continuous fixed bed is that it offers a larger surface area per unit volume resulting in a high mass transfer and a faster rate of effluent cleaning per unit volume of influent (Al-Rashdi et al. 2011). The output of the fixed bed is analyzed by plotting the fraction of the effluent concentration (C/Co) the breakthrough curve (Vilvanathan and Shanthakumar 2017). The breakthrough curve reflects the viability of adsorption, and the shape of the ideal breakthrough curve is sigmoidal or S-type (Carolin et al. 2017). Furthermore, the breakthrough curve also reflects the column conditions. Determining the shape of the breakthrough curve is an important aspect in designing the column (Arbabi and Golshani 2016).

A variety of mathematical models have been developed to test the efficacy and possible applications of columns for industrial operations (Patel 2019). Some of the most frequently used models for the evaluation of the fixed-bed columns are Thomas, Bed Depth Service Time, Adams-Bohart, and Yoon-Nelson (Fu and Wang 2011). Thomas model and Bohart-Adams model are based on mass transfer phenomenon and surface reaction rate theory, respectively (Hu et al. 2019). However, when the experimental time or bed volume is zero, the Thomas model has a fixed value, which is not in harmony with the ideal breakthrough curve (Han et al. 2020). Besides this, it is necessary to conduct a large number of experiments with repeated trials in order to find out the values of the model constants, which is time-consuming. Furthermore, the breakthrough curve and adsorption capacity of the adsorbent, under a given set of operating conditions, must be calculated in order to design an adsorption column (Gupta and Babu 2009). For this, mathematical models and computational simulations bring an advantage in terms of time and cost. However, statistical tools and machine learning techniques may provide an alternative approach for the development of new models.

The objective of this paper is to create a new mathematical model for the continuous fixed-bed column adsorption (down-flow) that relates the reactor parameters and the breakthrough curve. An attempt has been made to prove that there exists a fixed relation between the breakthrough curve and the reactor operating parameters and also, the set of parameters values in the relation is fixed for any given adsorbate–adsorbent pair. In this paper, the effect of various operating parameters on the adsorption was observed and the breakthrough curve trend was generalized to find the relationship between these parameters and the breakthrough curve’s arbitrary constants. The model is then confronted with experimental data (obtained from published research papers) and adjusted using tools of machine learning. Curve-fitting and multiple linear regression techniques were used to train and test the model developed. Rector parameters considered in the present study were bed height, flow rate and inlet metal concentration at constant temperature and pH.

Development of mathematical model (the VJSS model)

Tools and software

In the present work, an online graphing plotter, the Desmos Graphing calculator was used for statistical nonlinear curve fitting. A free to use software, the Gretl was used for linear regression.

Approach used for model development

Supervised machine learning is the basis for the modeling approach. Research articles (Kawamura et al. 1997; Yoshida and Takemori 1997; Murillo et al. 2004; Chu 2020) and books (Field 2002; Noh 2020) were referred to understand the nature of breakthrough curves and fixed-bed column reactors. These were used to choose an equation, which can fit all possible S-type curves into one equation with varying arbitrary constants. The equation of logistic function curve (used in Logistic Regression), a common sigmoid curve which does not have a fixed point at origin, was replaced with a well-known Avrami equation which has its one end fixed at origin (Fig. 1).

Fig. 1
figure 1

a Typical Logistic Function Curves. b Avrami Equation Curves Plotted

Full size image

In a supervised learning approach, the model must be first trained with known data (fixed-bed column studies in this case). Various research papers (Patel and Vashi 2012; Mashal et al. 2014; Qu et al. 2019; Patel 2020) were considered, and the breakthrough curve was fitted using the Desmos Graphing Calculator. The resulting arbitrary constants from the curve fitting were used to build a linear regression equation against the reactor operating parameters.

Breakthrough curve

The Avrami equation was considered to show the nature of the breakthrough curve (Sigmoid Curve) in the proposed model (Eq. 1)

$$y=1-{e}^{-k{ t }^{n}}$$
(1)

where y refers to \(\frac{{C}_{\mathrm{t}}}{{C}_{o}}\), t refers to time, and k and n are arbitrary constants

In Eq. (1), the arbitrary constant k is always positive and n is > 1 always irrespective of any other factor. The value of k and n depicts the steepness and spread of the curve. The values of k and n depend on the operation and reactor parameters such as bed height, flow rate, and initial concentration. The change in these reactor parameter values is responsible for the change in steepness and slope of the curve. Hence, for a fixed adsorbate–adsorbent pair the relation between the arbitrary constants and operating parameters does not change. In order to determine the breakthrough curve, it is necessary to elucidate this relation between the model arbitrary constants (k and n) and the reactor parameters for any given adsorbate–adsorbent pair.

In order to find out the value of k and n from the experimental data given in references (Patel and Vashi 2012; Mashal et al. 2014; Qu et al. 2019; Patel 2020), the method of superimposition of graph was used wherein the breakthrough plots from these references were superimposed with the axes on Desmos Graphing Calculator and scaled to match with those of the given plots. The rationale behind using this method for model fitting and validation is that these references offer experimental data in the form of plots only and do not provide exact numerical data.

In this method of determination of arbitrary constants, the value of the breakthrough curve’s coefficient of correlation R2 referred to herein as BC-R2 must be close to 1 to get the best fit.

Derivation of arbitrary constants relation (ACR)

The arbitrary constant relation (ACR) is the equation relating the arbitrary constants and the reactor operating parameters. The steps for determining the ACR relation involve performing linearity tests between individual operating parameters and the arbitrary constants and finding the ACR equation with ACR’s coefficient of correlation (ACR-R2). This test is conducted to test linearity between operating parameters and the arbitrary constants. As there are two arbitrary constants, namely k and n, it would be better to find a term that is a result of a function of these two parameters as both terms contribute to the steepness and spread of the curve. In order to obtain the term, Eq. 1 was simplified as shown below.

Simplifying Eq. 1 and taking natural log on both sides yields Eq. 2.

$$\mathrm{ln}(1-y)= -k{t}^{n}$$
(2)

After taking log10 on both the sides of Eq. 2

$$\mathrm{log}(-\mathrm{ln} (1-y)) = \mathrm{log} k +n \, \mathrm{log}\, t$$
(3)

Rearranging Eq. 3 results in Eq. 4

$$\mathrm{log }t =\frac{\mathrm{log}(- \mathrm{ln} (1-y))}{n}-\frac{\mathrm{log} \,k}{n}$$
(4)

For a static set of reactor/operational parameters and for a given adsorbate–adsorbent pair, \(\frac{-\mathrm{log}\, k }{n}\) is the constant term as the steepness and slope of the curve will remain the same. In order to identify the relationship between the arbitrary constants and the parameters, the linearity was tested between \(\frac{-\mathrm{log} \, k }{n}\) and the parameters. The case studies (Patel and Vashi 2012; Mashal et al. 2014; Qu et al. 2019; Patel 2020) were considered for model testing and validation. All the available data points on the plots in the references were used, and no data point was omitted without proper explanation. Only a few of the marked points are shown in the figures so that the points and curve below the fitted curve stay visible.

Adsorption of Pb (II) ions on Auricularia matrix waste

Qu et al. 2019 attained the breakthrough and saturation points for different bed heights, flow rates and initial concentration of metal ions. All points were marked (similar to those indicated using colored symbols) on the breakthrough curve in the background image to find the values of arbitrary constants (Figure S1 of supplementary information). Thomas model showed R2 ranging from 0.85 to 0.99 and Bohart-Adams model had R2 between 0.52 and 0.92 (Qu et al. 2019). However, the BC-R2 (from curve fitting) value for our model was > 0.99 in each case for the Auricularia matrix. This shows the closeness of the developed model with the experimental values obtained in the reference (Qu et al. 2019). The BC-R2 values are different from the linearity test R2 (LT-R2).

The results in Table 1 show that the R2 for the linearity test ranged between 0.96 and 0.99 and the SSR values were also very low, which indicates the existence of linear relationship between \(\frac{-\mathrm{log}\, k }{n}\) and the parameters.

Table 1 Results of curve fitting and linearity test for reference (Qu et al. 2019)
Full size table

Adsorption of acid yellow 17 dye on tamarind seed powder

Patel and Vashi 2012 gave the breakthrough points for each curve. Similar to Section "Adsorption of Pb (II) ions on Auricularia matrix waste", the experimental values in the background image were marked in the graph to find the arbitrary constant (Figure S2 of supplementary information).

The BC-R2 value for all the plots was very high. Some of the BC-R2 values were equal to unity, while all other values were > 0.99. The R2 values for the linearity tests were also high (0.98–0.99) and the value of SSR was also low indicating towards a linear relation (Table 2). These values show closeness of the model with the experimental values. This also proves it to be an effective working model that can replicate and show the data for the given adsorbate adsorbent pair up to a high accuracy level. As the curves with the same set of parameters plotted in the reference did not coincide and had different breakthrough and saturation points, the value of \(\frac{-\mathrm{log}\, k }{n}\) was different. Though the linear relation has been shown and the difference in value is not significant, the complete model determination was not continued due to the discrepancy.

Table 2 Results of curve fitting and linearity test for reference (Patel and Vashi 2012)
Full size table

Adsorption of ammonia ions on Jordanian Natural Zeolite

The graphs from (Mashal et al. 2014) were loaded on the online graphing calculator, and few experimental points were randomly marked on the graph after matching the axes. The points marked on the graph were used to determine the arbitrary constants (Figure S3 of supplementary information).

Similar to Sects. "Adsorption of Pb (II) ions on Auricularia matrix waste" and "Adsorption of acid yellow 17 dye on tamarind seed powder", the BC-R2 value was observed to be very high (> 0.98). The linear relation between the parameters and \(\frac{-\mathrm{log }\,k }{n}\) was clearly observed from Table 3. The range of LT-R2 was between 0.88 and 0.97, which is relatively low (as compared to Sects. "Adsorption of Pb (II) ions on Auricularia matrix waste" and "Adsorption of acid yellow 17 dye on tamarind seed powder"). This may be due to the variation in particle size of adsorbent, as it is important to keep at least one parameter varying to get a perfect linearity test result. A wide range of particle size means that the particle size is changing and must be considered. However, the particle size was in \(\mathrm{\mu m}\). Hence, the effect was not significant enough to decline the linear relation between parameters and \(\frac{-\mathrm{log} \,k }{n}\).

Table 3 Results of curve fitting and linearity test for reference (Mashal et al. 2014)
Full size table

Adsorption of heavy metals (chromium, nickel, zinc, cadmium, copper, lead) on activated charcoal from neem (Azadirachta Indica) leaf powder (AC-NLP)

Patel 2020 obtained breakthrough curves for six pairs of adsorbent–adsorbate. This dataset is very useful and effective to prove the existence of the linear relationship between parameters and \(\frac{-\mathrm{log} \,k }{n}\). In order to achieve this, the same approach was adopted where the plots were scaled on an online graph sheet and the points were marked to fit the curve (Figure S4 of supplementary information). The BC-R2 value is observed to be very high, and the linearity test results are tabulated in Table 4. The R2 values for the linearity tests were very close to 1, and SSR was very small which justifies the linear relationship.

Table 4 Results of curve fitting and linearity test for reference
Full size table

ACR and features of VJSS model

The BC-R2 or the coefficient of correlation for the breakthrough curve was very high in most of the cases. This indicates that the model is efficient in plotting any breakthrough curve (sigmoidal) without any restrictions. The model from here onwards will be referred to as the VJSS model. The term VJSS was coined from the name of the authors and does not have any significance of its own. With the defined VJSS model, it is important to determine the final ACR equation that relates the arbitrary constants and the parameters.

With the existence of linear relationship, lack of multi-collinearity between parameters and no heteroscedasticity in the data tested, it can be concluded that the ACR equation is a multiple linear regression model with \(\frac{-\mathrm{log} \,k }{n}\) and experimental/operational parameters as dependent and independent variables, respectively (Table 5).

Table 5 ACR parameters coefficients and multiple linear regression analysis for ACR equation
Full size table
$$\frac{-\mathrm{log}\, k }{n} = \Sigma {(\mathrm{MLR} \, \mathrm{coefficient})}_{i}{ . \, (\mathrm{parameter})}_{i}+ \, \mathrm{constant}$$
(5)

In Eq. 4, at \(\mathrm{log} \left(-\mathrm{ln} \left(1-y\right)\right)=0 ,\) the\(t ={10}^{ (\frac{-\mathrm{log}\, k }{n})}\). If the ACR equation is known, then this specific point in any breakthrough curve can be calculated without any experimentation. This point \(\left( {10^{{ \left( {\frac{{ - {\text{log}} k}}{n}} \right)}} , \left( {1 - \frac{1}{e}} \right)} \right)\) is referred to herein as VJSS point. This is the only point that can be determined without any direct estimation of arbitrary constants. Substituting the parameters in the ACR equation yields the time after which 63.21% (or \(\left(1-\frac{1}{e}\right)\times 100\) from VJSS point) of the adsorbate concentration remains in effluent. This is a fiscal advantage of using this model in design of a packed bed column as this point is obtained without any experimentation.

The MLR coefficients of parameters in the ACR equation referred to herein as ACR-CP are unique for an adsorbate–adsorbent pair. The ACR equation gives the value of \(\frac{-\mathrm{log}\, k }{n}\) and not the values of k and n. Hence, for finding the values of k and n, one more point is necessary other than VJSS point. Once the values of ACR-CP are determined, the breakthrough curve for any specific set of parameters can be predicted with high accuracy by experimentally determining just one point on the breakthrough curve.

Conclusion

  1. 1.

    The mathematical model developed in this work achieves a higher coefficient of accuracy as compared to other models and can be applied to a variety of data sets.

  2. 2.

    Unlike traditional models, the breakthrough curve can be predicted with only one point without any loss of accuracy for any given set of parameters using the ACR equation for adsorbate–adsorbent pair.

  3. 3.

    The VJSS model has high predictive ability and can predict any number of points on the curve with just one point determined experimentally.

  4. 4.

    The VJSS point can be determined without conducting experiments only by using the VJSS model, which saves time and is cost-effective.

  5. 5.

    The ACR equation allows for reactor operating parameters to be substituted directly to get the VJSS point, eliminating the need for constant intervals of determining effluent concentration.

  6. 6.

    The VJSS model requires a lesser number of experiments to obtain the sigmoidal breakthrough compared to traditional mathematical models, saving researchers time and effort.

  7. 7.

    The knowledge of the saturation limit of adsorbent can be used to predict when the saturation limit will be achieved if the reactor is run with a certain set of reactor parameters.

Overall, the findings of this work highlight the potential benefits of the VJSS model in various industries and provide a promising avenue for future research in this area.