Introduction

Urban flood is the volume of water that is beyond the drainage capacity of the city and leads to a series of problems and damages in the city. Infiltration system is a popular method of storm water management. The models of water flow in the unsaturated environment have been considered by scientists since the past. The most common model that has been presented so far is the Richards equation, which was first presented in 1931. The continuity (transport) equation is combined with Darcy’s law as momentum equation and Richards equation is obtained (Richards 1931). One of the simulation methods of water flow in unsaturated environment is numerical methods. Numerical methods of finite difference, finite elements, finite volumes, etc., are a set of methods that estimate the desired values in the equations by a mesh in the solution field, and many researchers used them to solve the Richards equation. Taheri Shahraiyni and Ataie Ashtiani (2009) compared finite difference designs for water flow in unsaturated soils. Xiao (2016) used meshless Petrov–Galerkin method for the one-dimensional solution of Richards equation and obtained acceptable results. Keita et al. (2021) used meshless Petrov–Galerkin method to analyze the Richards equation. Farahi et al. (2017) proposed a new model for simulating the hydraulic performance of an infiltration trench using the one-dimensional solution of Richards equation and the finite volume method. This model showed an accurate simulation of flow movement in unsaturated soil.

Despite many advantages, numerical methods have limitations. During the past years, many researchers have attempted to resolve these limitations, but still all the classical numerical methods have problems related to field meshing (Li et al. 2003). Recently, in addition to the above methods, a different approach is used for equation analysis and computational geometry discretization, which are known as particle-based and meshless methods. These methods use a set of scattered nodes in the problem domain along with a set of scattered nodes on the boundaries of the domain to represent the problem domain and boundaries (Liu 2002). Kanzari and Mariem (2017) used Kirchhoff transformation and Richards equation to simulate water flow in porous environments. Suk and Park (2019) numerically solved the Richards equation using the Kirchhoff transformation function to simulate the variable saturation flow in heterogeneous layered porous environments. Boujoudar et al. (2021a, b) modeled unsaturated flow through porous environments using RBF and Kirchhoff transformation. Therefore, according to the above, in this study, the combined form of the Richards equation was used to simulate the changes in water flow in the soil because this equation is applicable to both saturated and unsaturated soils and has more mass retention. Also, it can be used in layered soils. Until now, the Kirchhoff transformation seems to be very promising method for simulating unsaturated Richards equation. But there are some limitations in its use, especially when the Kirchhoff transformation is employed to solve nonlinear Richards equation based on specific constitutive relation such as Gardner relation. Despite widespread popular use of the Gardner constitutive relations, some people noted that exponential dependence of hydraulic conductivity on pressure head may not be representative of the full moisture range in real soils (Philip 1984; Khaleel and Relyea, 2001) and so applicability of Gardner model is limited compared to Brooks-Corey and van Genuchten models. Nevertheless, some scientists like Ji et al (2008) proved the applicability of Gardner relations by using Kirchhoff transformation in pseudo-heterogeneous layered porous media. But there was no research in this field in homogeneous soil. Therefore, in this research, for the first time, we investigated the Richards equation using the Gardner model with the Kirchhoff transformation. Then, for the first time, the numerical method, meshless Petrov–Galerkin method along with moving least squares approximation function and Spline weight function was used for the one-dimensional solution of Richards equation. Finally, after modeling, the results were compared with the results of other researchers.

Materials and methods

Governing equations

The meshless Petrov–Galerkin method is one of the real meshless methods because it does not require meshing over the domain of the problem at any of the analysis stages, including field variable approximation and numerical integration of weak form equations. This method solves the equations using the local weak form and was first presented by Atluri and Zhu (1998). In the proposed method, the domain is determined by a set of nodes that have no predetermined relationship. Then, local weak form equations and moving least squares approximation function are used to transform the problem into a system of linear or nonlinear equations. Also, Gaussian integration method is used to solve integral equations (Atluri and Shen 2005).

Moving least squares approximation function

Differential equations can be discretized using moving least squares approximation function. This function can provide a continuous approximation for the interpolation of the field function throughout the problem domain. Also, the ability to approximate with an order of consistency is one of the most important features of this function, which leads many researchers to use it to generate shape functions. The moving least squares approximation that describes the variable field locally by the coefficient of the polynomial matrix in the matrix of coefficients is expressed as follows (Liu and Gu 2005):

$$U^{h} \left( X \right) = \mathop \sum \limits_{j}^{m} p_{j} \left( X \right)a_{j} \left( X \right) = P^{T} \left( X \right)a\left( X \right) = \mathop \sum \limits_{I}^{n} \emptyset_{I} \left( X \right)U_{I}$$
(1)

where \(U^{h}\) \(\left( X \right)\) is the function of field changes in the studied range, \(P^{T} \left( X \right)\) is a vector of basic functions based on Pascal’s triangle, a(X) is the vector of coefficients, \(\emptyset_{I} \left( X \right)\) is the shape function, and \(U_{I}\) is a nodal parameter. The coefficient a(X) is obtained from minimizing the weighted discrete norm function \(L_{2}\) as the following linear equation:

$$a\left( X \right) = A^{ - 1} \left( X \right)B\left( X \right)U_{s}$$
(2)

where A, B and \(U_{s}\) are, respectively, obtained from the following relations:

$$A\left( x \right) = \mathop \sum \limits_{I}^{n} W\left( {X_{I} } \right)p\left( {X_{I} } \right)P^{T} \left( {X_{I} } \right)$$
(3)
$$B\left( X \right) = \left[ {B_{1} B_{2} \ldots B_{n} } \right] = \left[ {W_{1} p\left( {X_{1} } \right) W_{2} p\left( {X_{2} } \right) \ldots W_{n} p\left( {X_{n} } \right)} \right]$$
(4)
$$U_{s} = \left[ {U_{1} U_{2} \ldots U_{n} } \right]$$
(5)

Finally, the moving least squares approximation function is presented as follows:

$$U^{h} \left( X \right) = \mathop \sum \limits_{I}^{n} \mathop \sum \limits_{j}^{m} p_{j} \left( X \right)\left( {A^{ - 1} \left( X \right)B\left( X \right)} \right)_{ji} U_{I} = \mathop \sum \limits_{I}^{n} \emptyset_{I} \left( X \right)U_{I}$$
(6)

The base vector often includes the maximum number of monomials necessary to achieve minimal completeness. In a one-dimensional space, a complete polynomial base function of order l is expressed according to the following equation:

$$P^{T} \left( x \right) = \left\{ {\left. {1\;\; x \;\;x^{2} \ldots \,x^{l} } \right\}} \right.$$
(7)

and in a two-dimensional space

$$P^{T} \left( {X,Y} \right) = \left\{ {\left. {1 \;\;x \;\;y \;\;x^{2} \;\;xy \;\;y^{2} \; \ldots \; y^{l} } \right\}} \right.$$
(8)

In general, the base vector is based on Pascal’s triangle.

Weight function

The weight function plays an essential role in the performance of moving least squares approximation and should have the following features: the value of the weight function is positive in the support domain, zero outside the support domain, and the value of the weight function uniformly reduces with respect to the desired point. This function is fairly smooth on the boundaries and is used in different forms like Gaussian, Quartic and Spline. Since the spline weight function is used in this study, its calculation method is described below (Liu an Gu 2005):

$$W_{i} \left( X \right) = \left\{ \begin{gathered} \frac{2}{3} - 4\overline{r}_{i}^{2} + 4\overline{r}_{i}^{3} \quad \quad \quad \quad \quad \quad \overline{r}_{i} \le 0.5 \hfill \\ \frac{4}{3}4\overline{r}_{i} - 4\overline{r}_{i}^{2} + \frac{4}{3}\overline{r}_{i}^{3} \quad \quad \quad \quad 0.5 < \overline{r}_{i} \le 1 \hfill \\ 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \overline{r}_{i} > 0.5 \hfill \\ \end{gathered} \right.$$
(9)
$$r_{i} = \frac{{d_{i} }}{{r_{w} }} = \frac{{\left| {x - x_{i} } \right|}}{{r_{w} }}$$
(10)

\(r_{w}\) is the influence radius of the nodal point. For each point, \(r_{w}\) should be selected in such a way that the number of nonzero weights is greater than the number of the polynomials (N > M).

Discretization of Richards equation

Understanding the process of infiltration and movement of flow in porous environments is very necessary for flood control. Several models have been developed to describe flow infiltration and flow movement in the porous soil, among which the Richards equation has high accuracy and efficiency. This equation is obtained from the integration of Darcy’s and continuity equations, and it is defined in the form of a mixed-form as the following equation (Richards 1931):

$$\frac{\partial }{\partial z}\left( {K\left( {\frac{\partial h}{{\partial z}}} \right)} \right) - \frac{\partial K}{{\partial z}} = \frac{\partial \theta }{{\partial t}}$$
(11)

where θ is the volumetric soil water content (\(L^{3} /L^{3}\)), h is the pressure head (L), and K is the unsaturated hydraulic conductivity of the soil (L⁄T), which is obtained by the equation K = \(K_{s} K_{r}\). In this regard, K_s is the saturated hydraulic conductivity, which is as follows:

$$K_{s} = \frac{\rho gk}{\mu }$$
(12)

where ρ is water density, g is the gravitational acceleration, k is the inherent permeability of the environment, and μ is the dynamic viscosity of the fluid. \(K_{r}\) is the relative hydraulic conductivity of water, indicating the effect of partial saturation. In unsaturated soils, soil water content and hydraulic conductivity are also in unsaturated conditions and dependent on each other and change by changing each of the other parameters. There are several models to describe the relationship between specific hydraulic parameters, including Brooks and Corey (1964), Genuchten (1980) and Mualem (1976). Given that Gardner’s exponential model is one of the widely used models to describe the physical properties of unsaturated porous environments, this function has been selected in this study.

Gardner’s model describes volumetric soil water content and the relationship between hydraulic conductivity and pressure head in the following exponential form (Gardner 1958).

$$k_{r} = \left\{ {\begin{array}{*{20}c} { e^{\lambda h} \;\;\;\;\; {\text{for }} h < 0} \\ {1 \;\;\;\;\;\;\;\;{\text{for}} h \ge 0} \\ \end{array} } \right.$$
(13)
$$\theta = \left\{ {\begin{array}{*{20}c} {\theta_{r} + \left( {\theta_{s} - \theta_{r} } \right) e^{\lambda h} \;\;\;\; {\text{for }} \;\;\;\; h < 0} \\ {\theta_{s} \;\;\;\; {\text{for }} \;\;\;\; h \ge 0} \\ \end{array} } \right.$$
(14)

where λ is a parameter related to soil pore size distribution (1⁄L), \(\theta_{r}\) is residual soil water content (-), and \(\theta_{s}\) is saturated soil water content (-). By applying the above equations to Eq. (11), the Richards equation is obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {\frac{\partial }{\partial z}\left( {K_{s} \frac{\partial \varphi }{{\partial z}}} \right) - \frac{\partial }{\partial z}\left( {K_{s} K_{r} \left( {\frac{\partial Z}{{\partial z}}} \right)} \right) = \lambda \left( {\theta_{s} - \theta_{r} } \right)\frac{\partial \varphi }{{\partial t}} {\text{for}} \;\;\;\;\;\; h < 0 } \\ {\frac{\partial }{\partial z}\left( {K_{s} \frac{\partial \varphi }{{\partial z}}} \right) - \frac{\partial }{\partial z}\left( {K_{s} \left( {\frac{\partial Z}{{\partial z}}} \right)} \right) = 0 {\text{for}} \;\;\;\;\;\;\;\; h \ge 0} \\ \end{array} } \right.$$
(15)

Since the Richards equation is highly nonlinear, Kirchhoff transformation has been used to reduce the nonlinearity of the above equation. So far, Kirchhoff transformation is considered as a very promising method to simulate the unsaturated Richards equation because Kirchhoff transformation head changes due to its integral nature are much smaller than the pressure head changes, so the numerical errors can be effectively reduced (Pullan 1990; Bakker and Nieber 2004; Ameli et al. 2013; Friedman and Gamliel 2019). The method is very stable and conserves mass, allowing a very fast solution, using Picard’s iteration method, as opposed to the expensive Newton–Raphson iterations that are often required with traditional formulas and provide correct solutions (Lehmann and Ackerer 1998). In fact, by applying Kirchhoff transformation in this way, the strongly nonlinear Eq. (15) is reduced to a weakly nonlinear form.

Kirchhoff transformation is as follows:

$$\varphi \left( h \right) = \mathop \smallint \limits_{ - \infty }^{h} K_{r} \left( s \right) ds$$
(16)

where φ(h) is a transformation variable or Kirchhoff pressure head. By applying Eq. (13) to the above equation, the Kirchhoff transformation is obtained as follows:

$$\varphi \left( h \right) = \left\{ {\begin{array}{*{20}c} {\frac{1}{\lambda }e^{\lambda h} \quad \quad \quad {\text{for}}\quad \quad \quad h < 0} \\ {\frac{1}{\lambda } + h \quad \quad \quad {\text{for}} \quad \quad \quad h \ge 0} \\ \end{array} } \right.$$
(17)

By replacing the above equation in Eq. (15), the Richards equation is obtained as follows:

$$\begin{aligned} C\frac{\partial \varphi }{{\partial t}} & = \frac{\partial }{\partial z}\left( {K_{s} \frac{\partial \varphi }{{\partial z}}} \right) - \frac{\partial }{\partial z}\left( {D\varphi } \right) - \frac{\partial }{\partial z}\left( G \right) \\ C & = \left\{ {\begin{array}{*{20}l} {\lambda \left( {\theta_{s} - \theta_{r} } \right)} \hfill & {{\text{for}}} \hfill & {\varphi < \frac{1}{\lambda }} \hfill \\ {0 } \hfill & {{\text{for}}} \hfill & {\varphi \ge \frac{1}{\lambda }} \hfill \\ \end{array} } \right. \\ D & = \left\{ {\begin{array}{*{20}l} {K_{s} \lambda } \hfill & {{\text{for}}} \hfill & {\varphi < \frac{1}{\lambda }} \hfill \\ {0 } \hfill & {{\text{for}}} \hfill & { \ge \frac{1}{\lambda }} \hfill \\ \end{array} } \right. \\ D & = \left\{ {\begin{array}{*{20}l} {K_{s} \lambda } \hfill & {{\text{for}}} \hfill & {\varphi < \frac{1}{\lambda }} \hfill \\ {0 } \hfill & {{\text{for}}} \hfill & {\varphi < \frac{1}{\lambda }} \hfill \\ \end{array} } \right. \\ \end{aligned}$$
(18)

To solve the above equation, Picard’s method, fixed point iteration method, is used. By applying Picard’s method to the mixed-form of Richards equation, Eq. (18) is defined as follows:

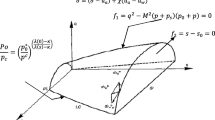
$$C^{n + 1, m} \frac{{\varphi^{n + 1, m + 1} - \varphi^{n} }}{\Delta t} = K_{s} \frac{{\partial^{2} \varphi^{n + 1, m + 1} }}{{\partial z^{2} }} - D^{n + 1, m} \frac{{\partial \varphi^{n + 1, m + 1} }}{\partial z} - \frac{{\partial G^{n + 1, m} }}{\partial z}$$
(19)

where n and m represent time and iteration, respectively. The above equation is discretized using Petrov–Galerkin method and weighted residuals:

$$C^{n + 1, m} \iint\limits_{\Omega } {W_{i} }\frac{{\varphi^{n + 1, m + 1} - \varphi^{n} }}{\Delta t} = K_{s} \iint\limits_{\Omega } {W_{i} }\frac{{\partial^{2} \varphi^{n + 1, m + 1} }}{{\partial z^{2} }} - D^{n + 1, m} \iint\limits_{\Omega } {W_{i} }\frac{{\partial \varphi^{n + 1, m + 1} }}{\partial z} - \iint\limits_{\Omega } {W_{i} }\frac{{\partial G^{n + 1, m} }}{\partial z}$$
(20)

The first and second terms on the right side of the above equation become simpler by integrating part by part, and the following equation is obtained:

$$\begin{aligned} C^{n + 1, m} \iint\limits_{\Omega } {W_{i} }\frac{{\varphi^{n + 1, m + 1} }}{\Delta t} - C^{n + 1, m} \iint\limits_{\Omega } {W_{i} }\frac{{\varphi^{n} }}{\Delta t} & = - K_{s} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}\frac{{d\varphi^{n + 1, m + 1} }}{dz}d\Omega \\ & + D^{n + 1, m} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}\varphi^{n + 1, m + 1} d\Omega - \iint\limits_{\Omega } {W_{i} }_{i} \frac{{\partial G^{n + 1, m} }}{\partial z} \\ \end{aligned}$$
(21)

The estimated value considered for the unknown is:

$$\varphi^{n + 1, m + 1} = \mathop \sum \limits_{i = 1}^{m} \varphi \left( t \right)^{n + 1,m + 1} \times {\text{phi}}\left( z \right)$$
(22)

By replacing Eqs. (22) in (21):

$$\begin{aligned} W_{i} C^{n + 1, m} {\text{phi}}\left( z \right)\iint\limits_{\Omega } {\frac{{\varphi \left( t \right)^{n + 1,m + 1} }}{\Delta t}} - W_{i} C^{n + 1, m} \frac{{\varphi^{n} }}{\Delta t} & = - K_{s} \varphi \left( t \right)^{n + 1,m + 1} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}\frac{{d{\text{phi}}\left( z \right)}}{dz}d\Omega \\ & + D^{n + 1, m} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}\varphi \left( t \right)^{n + 1,m + 1} {\text{phi}}\left( z \right)d\Omega - \iint\limits_{\Omega } {W_{i} }\frac{{\partial G^{n + 1, m} }}{\partial z} \\ \end{aligned}$$
(23)

Finally, a linear form of the equation has been obtained, and the stiffness, unknown and load matrices are given below:

$$K = \frac{{W_{i} C^{n + 1, m} {\text{phi}}\left( z \right)}}{\Delta t} + K_{s} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}\frac{{d{\text{phi}}\left( z \right)}}{{{\text{d}}z}}d\Omega - D^{n + 1, m} \iint\limits_{\Omega } {\frac{{dw_{i} }}{dz}}{\text{phi}}\left( z \right){\text{d}}\Omega$$
(24)
$$U = \varphi^{n + 1, m + 1}$$
(25)
$$F = \varphi^{n} \frac{{W_{i} C^{n + 1, m} }}{\Delta t} - \iint\limits_{\Omega } {W_{i} }\frac{{\partial G^{n + 1, m} }}{\partial z}$$
(26)

Then, Richards equation modeling algorithm is specified: Fig. 1.

Fig. 1
figure 1

Richards equation modeling algorithm using local meshless Petrov–Galerkin method

Full size image

Evaluation of model performance

The criterion used in this study is the root mean square error (RMSE) and Nash–Sutcliffe efficiency coefficient (\(NS\)), and their relationship is as follows:

$${\text{RMSE}} = \sqrt {\frac{1}{n}\sum \left( {H_{{{\text{calc}}}} - H_{{{\text{obsr}}}} } \right)^{2} }$$
(27)
$${\text{NS}} = 1 - \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {H_{{{\text{calc}}}} - H_{{{\text{obsr}}}} } \right)^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\overline{H}_{{{\text{obsr}}}} - H_{{{\text{obsr}}}} } \right)^{2} }}$$
(28)

where n is the number of data, \(H_{{{\text{calc}}}}\) is the pressure head calculated by meshless Petrov–Galerkin method, and \(H_{{{\text{obsr}}}}\) is the observed pressure head.

Results and discussion

To evaluate the accuracy and trustworthiness of the model prepared from the simulation of infiltration flow, the data of several articles have been used, which are examined below.

Example 1 (comparison with analytical solution)

One of the conventional methods to verify the results of the numerical solution of a model is to compare it with the results of the analytical solution of that model (Phoon et al. 2007). There are many models to describe water infiltration in soil. One of these models is Green–Ampt equations. Consider a column of soil with a height of L that is first dry and then water begins to infiltrate into the soil. After infiltration, a pond of water is kept at the ground level and the pressure head is kept at zero. This problem is known as one-dimensional Green–Ampt problem (Green & Ampt 1911). Tracy (2006) attempted to analytically solve the Richards equation under Green–Ampt conditions. In the initial test, we compare the results of the model presented in this study with the analytical solution of the Richards equation by Tracy. In this regard, we considered a column of soil with a thickness of 10 m and λ of 2 × 10–5 in Gardner’s exponential model. Saturated hydraulic conductivity, and saturated and residual water content are equal to 10–4 (m/h), 0.35 and 0.14, respectively (Lu and Likos 2004). The initial conditions of the soil under drought and equal to 10 m and Dirichlet boundary condition are as follows:

$$\left\{ {\begin{array}{*{20}c} {h\left( {z,0} \right) = h_{d} } \\ {h\left( {0,t} \right) = h_{d} } \\ {h\left( {L,t} \right) = 0 } \\ \end{array} } \right. - - - - - - \to \left\{ {\begin{array}{*{20}c} {K\left( {z,0} \right) = K_{s} e^{{\lambda h_{d} }} } \\ {K\left( {0,t} \right) = K_{s} e^{{\lambda h_{d} }} } \\ {K\left( {L,t} \right) = K_{s} } \\ \end{array} } \right.$$
(29)

where \(h_{d}\) is the initial compressive head in dry soil. Dirichlet boundary condition is applied using the following analytical solution (Tracy 2006):

$$\overline{h}_{t} \left( {z,t} \right) = \frac{{2\left( {1 - e^{{\alpha_{g} h_{d} }} } \right)}}{Lc}e^{{\frac{{\alpha_{g} \left( {L - z} \right)}}{2}}} \mathop \sum \limits_{k = 1}^{m} \left( { - 1} \right)^{k} \left( {\frac{{\lambda_{k} }}{{\mu_{k} }}} \right){\text{sin}}\left( {\lambda_{k} z} \right)e^{{ - \mu_{k} t}}$$
(30)
$$\mu_{k} = \frac{1}{c}\left( {\frac{{\alpha_{g}^{2} }}{4} + \lambda_{k}^{2} } \right)$$
(31)
$$\overline{h}\left( {z,t} \right) = \overline{h}_{t} \left( {z,t} \right) + \overline{h}_{s} \left( z \right)$$
(32)
$$\overline{h}_{s} \left( z \right) = \left( {1 - e^{{\alpha_{g} h_{d} }} } \right)\frac{{1 - e^{{ - \alpha_{g} z}} }}{{1 - e^{{ - \alpha_{g} L}} }}$$
(33)
$$h\left( {z,t} \right) = \frac{1}{{\alpha_{g} }}{\text{ln}}\left( {\overline{h}\left( {z,t} \right) + e^{{\alpha_{g} h_{d} }} } \right)$$
(34)

Finally, to evaluate the solution of the Richards equation by meshless Petrov–Galerkin method, the analytical solution of the equation under the above initial and boundary conditions for 1 h was used. All numerical problems in this article are the result of a code written by the author using MATLAB 2018. Then, the suction profile modeled by the numerical model proposed in this article is compared with the suction profile calculated by the analytical solution of the Richards equation by Tracy (2006) at different times.

Figure 2 shows the suction profile modeled by the model presented in the present study as a continuous line. As shown, there is a high agreement between that profile and the analytical solution. Table 1 shows errors of different methods at different times. As shown, over time, the results of numerical and analytical solutions are closer together, indicating that meshless Petrov–Galerkin method is a suitable choice for the one-dimensional solution of Richards equation.

Fig. 2
figure 2

Comparison of suction profile modeled by meshless Petrov–Galerkin method and analytical solution of Richards equation

Full size image
Table 1 Calculation of RMSE and NS at different times for soil suction profile (m)
Full size table

Example 2 (comparison with laboratory data)

In this problem, one-dimensional infiltration of water into the sandy soil column is investigated. To simulate this model, a plexiglass column has been used in vitro. The length of this soil column is 70 cm, and its cross-section is a square with a side of 5 cm. Measured values of water content at different depths and times were reported by Haverkamp et al. (1977). In this problem, primary and boundary conditions governing are as follows:

$$\left\{ {\begin{array}{*{20}c} {h\left( {0,t} \right) = - 20.7 {\text{cm}}} \\ {h\left( {70,t} \right) = - 61.5\; {\text{cm}}} \\ {h\left( {L,0} \right) = - 61.5 {\text{cm }}} \\ \end{array} } \right.$$
(35)

Haverkamp et al. used Gardner’s water content curve and hydraulic conductivity models as follows:

$$\theta = \theta_{r} + \frac{{A\left( {\theta_{s} - \theta_{r} } \right) }}{{A + h^{B} }}$$
(36)
$$k\left( h \right) = k_{s} \frac{D }{{D + h^{c} }}$$
(37)

They determined the parameters of the above model as follows.

$$\theta_{s} = 0.287, \theta_{r} = 0.075,A = 1.611*10^{6} ,B = 3.96, K_{s} = 34{\text{cm}}/h, D = 1.175*10^{6} , C = 4.74$$

Then, the pressure load profile after 360 s was calculated using meshless Petrov–Galerkin method. Figure 3 shows the calculation results as a continuous line along with the laboratory data as a circle. As shown, the results obtained from the solution of the numerical method and the laboratory data match very well. RMSE and NSH in this example are 0.97 and 0.96 cm, respectively, confirming the above results.

Fig. 3
figure 3

Comparison of the suction profile modeled by meshless Petrov–Galerkin method and the laboratory data (Havercamp et al. 1977)

Full size image

Example 3 (comparison with finite difference method)

Suk and Park (2019) considered the one-dimensional flow of water in homogeneous porous environments under three different scenarios. Parameter values and initial and boundary conditions for simulation are shown in Fig. 4. Under all scenarios, the upper boundary was Dirichlet boundary condition with pressure head of -75 cm, while the lower boundary was Dirichlet boundary condition under three scenarios with pressure head of -200, -400 and -600 cm. Initial pressure head, exactly like Dirichlet boundary condition at the lower boundary, was -200, -400, and -600 cm corresponding to each scenario. In this section, we will investigate the Richards equation under the above conditions. Figure 5 shows the pressure head profile under three scenarios using the method proposed in this study. In this example, the mesh dimensions were 0.01 cm and the time step was 0.001 s. As shown, the drawn profiles are in good agreement with the results of Suk and Packer (2019) and acceptable results were obtained. RMSE and NSH in this example are 0.99 and 0.98 cm, respectively.

Fig. 4
figure 4

Domain of interest, initial and boundary conditions (Suk and Park 2019)

Full size image
Fig. 5
figure 5

Comparison of the suction profile modeled by meshless Petrov–Galerkin method and the numerical solution of the Richards equation (Suk and Park 2019)

Full size image

Example 4 (comparison with MQ-RBF)

The last example to investigate the accuracy of the model’s performance is a one-dimensional infiltration problem whose numerical solution is available. Boujoudar et al. (2021a, b) attempted to numerically solve the Richards equation by MQ-RBF and reached acceptable results. They simulated the one-dimensional infiltration problem using a computational domain of 50 m and set the soil parameters as \(\theta_{r}\) = 0.15, \(\theta_{s}\) = 0.45, \(K_{s} = 0.1\left( {{\text{m}}/{\text{day}}} \right)\). This numerical example was with λ = 0.1, 0.2, 0.3 and 0.4 (m−1). The initial conditions of the soil under drought and equal to −20 m and Dirichlet boundary conditions are as follows: the upper boundary has a fixed pressure head of zero, and the lower boundary has a constant pressure head of −20. Numerical simulation of Richards equation for different values of λ and using correct values of shape parameter coefficient was done by trial-and-error method and acceptable results were obtained, which are shown in Fig. 6. As shown, for all values of λ at all times, the mentioned parameter has reasonable values, and this indicates the high accuracy of meshless Petrov–Galerkin method in numerical modeling to simulate flow in unsaturated soils. RMSE and NSH in this example are 0.99 and 0.99 cm, respectively. As shown, the size of λ had no significant effect on the performance of the model, but by increasing the value of λ, the dimensionless magnitude of the base domain should be reduced to maintain the stability of the method.

Fig. 6
figure 6

Comparison of the time evolution of the suction modeled by meshless Petrov–Galerkin method and the numerical solution of the Richards equation (Boujoudar et al 2021a, b)

Full size image

Conclusion

In this study, meshless Petrov–Galerkin method was used for one-dimensional solution of the mixed formulation of Richards equation, which has excellent results of mass balance, with water movement in unsaturated soil. Since the Richards equation is one of the nonlinear equations, Kirchhoff transformation and Picard’s iteration method were used to solve it to reduce its nonlinearity. After solving the above equation, to investigate its performance, the Richards equation was verified by different analytical solution methods, laboratory data, finite difference method and MQ-RBF; and the relative error of this method was calculated. Then, the results were compared in the form of suction profiles. The comparison results showed that all the investigated methods had an assessment criterion of root mean square error from 0.09 to 1.02 cm and Nash–Sutcliffe efficiency coefficient of 0.96 to 0.99 which is within an acceptable range, but compared to the above 4 methods, analytical solution and MQ-RBF, it obtained a better solution at the verification stage. The high consistency of the results shows that meshless Petrov–Galerkin method for one-dimensional solution of the Richards equation is suitable in terms of accuracy, efficiency and stability.