Abstract
Streamflow forecasting has always been important in water resources management, particularly the peak flow, which often determines the seriousness of the impending flood. However, the highly imbalanced flow distribution often hinders the machine learning algorithm's performance. In this paper, streamflow forecasting was approached through the formulation of two distinct machine learning problems: categorical streamflow forecast and regression streamflow forecast. Due to the distinctive characteristics of these two adopted forms, selecting the correct algorithm for the machine learning problem along with their hyperparameter tuning process is critical to the realization of the desired results. For the distinct streamflow formulated scenarios, three neural network algorithms and their hyperparameter tuning strategy were investigated. The comparative empirical studies had revealed that formulated categorical-based streamflow forecast is a better choice than a regression-based streamflow forecast, regardless of the algorithms used; for instance, the f1-score of 0.7 (categorical based) is obtained compared to the 0.53 (regression based) for the LSTM in scenario 1 (binary). Furthermore, forest-based algorithms were investigated and shown to be superior at forecasting high streamflow fluctuations in situations featuring low-dimensional streamflow input. Besides, encoding the streamflow time series as images (input) for forecasting purposes would require a thorough analysis as there is a discrepancy in the results, revealing that not all approaches are suitable for streamflow image transformation. The functional ANOVA analysis provided evidence to substantiate the Bayesian optimization results, implying that the hyperparameters were effectively optimized.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The growing usage of temporal data has prompted many research and development efforts in time series analysis, particularly with time series classification (TSC) and time series forecasting (TSF) (Sagheer and Kotb 2019). Time series in the medical domain (Chen et al. 2020; Ruiz et al. 2021), business and financial domain (Bukhari et al. 2020), cyber-security (anomaly detection) (Berman et al. 2019), and other real-world applications are examples that require extensive time series analysis. Following such a definition, the time series of streamflow may also be addressed in both studies. In the hydrology context, classification refers to the categorical-based streamflow forecast (e.g., probability of wet/dry conditions), whereas forecasting refers to regression-based (monthly, annually, etc.) streamflow forecast. Both of which have significant applications. A categorical-based streamflow forecast, for example, provides information on the likelihood of certain events occurring, such as the likelihood of having higher streamflow than a fixed threshold. On the other hand, regression-based streamflow forecasting provides information on the amount of streamflow, such as over a daily, monthly, or seasonal timescales. The benefits of accurate streamflow forecasting are evident in situations where inefficient water resource planning, design, and operation are called for (Pham et al. 2021; Zhu et al. 2022).
Machine learning is predominantly an area of artificial intelligence and is a crucial component of digitalization solutions that have garnered significant attention in the digital arena (Zeinali et al. 2021)Rahman et al. 2022; Ray 2019; Wäldchen et al. 2018). In a machine learning problem, both time series analyses are expressed differently. For instance, verifying dichotomous occurrences would need the pre-defining of the threshold, which will categorize whether the events fall below or above the criterion, where direct forecasting would not require such efforts. Machine learning techniques (data-driven-based models), such as artificial neural networks (ANNs), support vector machines (SVMs), and even deep learning (DL), have become prominent among the various models used in the hydrological field. Forest-based algorithms, which are less computationally expensive than neural network algorithms, are another popular machine learning technique. Several studies have been conducted that use forest-based algorithms as a benchmark for comparison, such as the study by Chaplot (2021). Sihag et al. (2021) demonstrated that soft computing techniques were capable of estimating Manning’s n value, with the M5P model being superior to the random tree (RT) and random forest (RF). Reis et al. (2021) showed that the inclusion of catchment attributes on artificial intelligence (AI) approaches, such as the multivariate adaptive regression (EARTH), multiple linear regression (MLR), and the random forest (RF) models, improved the daily streamflow forecasting. However, while the proposed approaches performed well, occurrences of erroneous predictions of high streamflow can significantly cause an impact, particularly in flood forecasting, where peak flow prediction is critical. Chong et al. (2020) observed that hydrological parameters often displayed a lag tendency when using the ANN as a forecasting model. Hybridization, data assimilation, and data decomposition are other techniques for improving machine learning approaches (He et al. 2022; Kumar et al. 2022). Nevertheless, most research in the literature focused on regression-based streamflow prediction, while the categorical-based streamflow forecast is rarely used. It should be mentioned that a categorical streamflow forecast differs from a probabilistic streamflow forecast in that the latter is still regarded as a regression problem. Ensemble model prediction, for example, is a sort of probabilistic rainfall forecast where the outputs are a set of combined regression forecasts produced from many models trained on the same training dataset (Ndione et al. 2020). That being said, due to the differences in attributes between these two adopted forms, utilizing the correct algorithm for the machine learning problem is crucial for achieving the desired results.
Following the recent success of the CNN, a deep learning algorithm in image identification, researchers looked for these complex machine learning algorithms for the TSC (Pan et al. 2019; Wang and Oates 2015). In order to preserve the temporal domain of the TSC, time series are recently transformed into series of images utilizing imaging approaches such as the Gramian transition field (GTF), recurrence plots (RP), and Markov transition fields (MTF), where these were recently adopted to solve TSC problems. Financial forecasting (Barra et al. 2020), traffic time series (Huang et al. 2021), electric residential load forecasting (Estebsari and Rajabi 2020), and other applications have witnessed an increase in accuracy from using image transformation of time series. Although machine learning algorithms do not necessitate prior assumptions about the underlying relationships, several issues must be addressed to get reliable findings. The hyperparameter tuning approach and interpretability are the primary concerns for a machine learning algorithm (Schratz et al. 2019). The former approach aims to explicitly find a set of hyperparameters that can achieve the best performance. This stage is perhaps the most crucial since a successful algorithm is based on the appropriate selection of hyperparameters, which can be accomplished manually or using a recent automated technique (Probst et al. 2019; van Rijn and Hutter 2018). Although both methods can effectively guide the algorithms toward a better result, manual calibration is much more complicated than an automatic one, due to the complex interaction between the various hyperparameters of an algorithm (Zhang et al. 2021). Adopting the Bayesian optimization has the following advantages: (1) a balanced trade-off between the exploitation of available information and exploration of uncertainty areas, and (2) reduced computational run time due to its informative feedback, which guides the searching procedure. It is a competent optimizer in applications worldwide, including robotics (Jaquier et al. 2020), flow simulation (Shin et al. 2020), adaptive Monte Carlo tuning (Balandat et al. 2020), and so on. Another prevalent difficulty is the interpretability (Meddage et al. 2022). It is critical to understand the efficacy of hyperparameters and how they interact to develop a model efficiently. Also, further analysis of the optimized hyperparameters from the Bayesian Optimization (BO) is required to quantify their impact on model performance and validate their results. Functional ANOVA (fANOVA) analysis, proposed by (Hutter et al. 2014), was used in this study to improve the interpretability of hyperparameter tuning.
In this context, this paper targets the following open questions: How good is machine learning, including deep learning, in categorical-based and regression-based streamflow forecasting? What type of hyperparameters works best for each task? Can a pure feature learning algorithm address the problem of streamflow data transformation based on the GAF, MTF, and RP? The rest of the paper is structured as follows. The second section introduces some background materials concerning the algorithms used, formulation of machine learning problems, and searching procedure of hyperparameters. Three neural network algorithms were introduced and explored in the third section. Meanwhile, the streamflow forecast was handled by formulating two distinct machine learning problems: categorical-based streamflow forecasts and regression-based streamflow forecasts. Following which, the outcomes of the Bayesian optimization and ANOVA analysis are also presented. The fourth section draws the recommendations for future research and conclusion.
Methodology
Study area
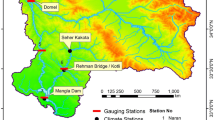
Johor is a coastal state located on Peninsular Malaysia's east coast, near the border with Singapore, as shown in Fig. 1, with a 400-km shoreline on both the east and west coastlines. With the northeast monsoon season blowing from the South China Sea from November to February and the southwest monsoon from May to September, it is well renowned for its tropical rainforest habitat. 1788 mm of rainfalls annually on average. It is predicted that the temperature ranges from 21 to 32 °C, with an average of 26.7 °C, and that the relative humidity on an average is 84%. The main river in Johor state is the Johor River, with an approximate length of 130 km and an area catchment of 2600 km2. The average, minimum, and maximum annual streamflow measured from 1965 to 2008 is tabulated as shown in Fig. 2. The Sayong, Lebam, Linggui, and Tiram Rivers are its primary tributaries. The streamflow data for this 44-year research is sourced from the Malaysia's Department of Irrigation and Drainage (DID).
Data formulation
Classification-based and regression-based formulation
The nature of the issues at hand, both the categorical-based and the regression-based streamflow forecasts, necessitates different data formulations. In a univariate time series, there is an input \(x\) (streamflow history information), an unknown function \(f:{ }x{ }y\) (via the artificial neural network), and an output y (streamflow 1 month ahead). An input–output space (\(X,{ }Y\)) consists of pairs of \(\left( {x1,{ }y1} \right),{ } \ldots ,{ }\left( {xn,{ }yn} \right)\) examples, where \(yn\) is the target label for categorical-based streamflow forecast or target value for regression-based streamflow forecast. It should be noted that classifying streamflow based on a fixed threshold may not be applicable in all regions. For instance, the pre-defined threshold for a watershed may not apply to another watershed of different precipitation intensities. For a fair comparison of the monthly streamflow across different stations, the flow is split according to three quartiles: (1) first quartile (\(< 25{\text{th}}\)) represents the low flow, the fourth quartile represents the high flow (\(> 75{\text{th}}\)), and the two quartiles (\(25{\text{th}} < {\text{flow}} < 75{\text{th}}\)) represents the moderate flow. Prior to any ANN training, normalization is necessary for better scalability. Normalizing data accelerates the learning process or dramatically speeds up the computational process, resulting in faster convergence, and are defined as below: \(x_{i} = \frac{{x_{i} - x_{\min } }}{{x_{\max } - x_{\min } }}\).
Data encoding as image formulation
Time series are often expressed in one-dimensional scale, either as a univariate time series with a rolling window feature or as a multivariate time series with lag characteristics; as input to the model. Encoding the time series data into an image representation for the deep learning model to learn the underlying patterns is another approach used in this paper. Three methods: the GAF, MTF, and RP were used to encode the streamflow time series as a set of sequential images. Since time grows as location moves from top-left to bottom-right, such data communication utilizing the suggested way can keep the temporal dependency.
Bayesian optimization (BO)
Hyperparameter tuning of a neural network can be considered as one of the many optimization problems in machine learning, where the objective function, \(f\), is a black box function. There is no analytical form to express the objective function or know its derivatives, and they can be computationally expensive. Therefore, BO, a sequential design strategy that is globally used to minimize a black box function in a minimum number of steps, is quite useful. The BO incorporates prior belief \(f\), uses the sample drawn from \(f\) to update the current prior, and computes the posterior belief that better approximates \(f\). The sequential strategy in the BO implies that the whole process in the BO will be iterated until a stopping criterion is achieved. In the BO, a surrogate model is used to approximate the objective function, and the selection of the sample drawn from \(f\) is based on the acquisition function.
Early termination rules
Given the propensity of neural networks to overfit as model complexity increases, an early termination mechanism is introduced prior to executing the BO. When the model's performance on the validation set deteriorates, the model is halted from training. If early termination is satisfied, the model obtained due to this termination will have a better generalization than a fully trained model with the lowest training error.
Acquisition function
In the BO, acquisition functions are responsible for guiding how the parameter sample should be explored within a search domain. There is usually a trade-off between exploitation and exploration search to reach the targeted goal. Exploitation search prioritizes solutions closer to the current best solution, whereas exploration search concentrates on the unexplored region. In this paper, the adopted acquisition function was the expected improvement (EI) due to its simplicity. Suppose that \(f^{\prime}\) is the minimum value among the currently found \(f\). The EI evaluates another point in which the obtained new \(f\) will improve \(f^{\prime}\). The evaluation function can be defined as:
This function corresponds to the improvement ‘\(f^{^{\prime}} - f\left( x \right)\)’ made when \(f\left( x \right)\) is better (lower value) than f′. The acquisition function based on EI can be defined as: where z can be computed as:
where \(\Phi \left( z \right)\) and ϕ(z) depict the cumulative distribution function (CDF) and probability distribution function (PDF) of the standard normal distribution, respectively. The point x at which returns the maximum value of EI will be selected. The general BO framework is shown in Fig. 3.
Machine learning algorithms and their hyperparameters
ANN algorithm
The ANN is a parametric model with a collection of parameters, such as weights and bias, that are trainable. It has several hyperparameters that need tuning, such as the learning rate and the hidden layer size. Unlike the CNN, it contains just a fully connected layer, in which each neuron is connected to all other neurons, as shown in Fig. 4. Table 1 summarizes the search space configuration and their respective hyperparameters.
CNN algorithm
In the CNN, the fundamental building components are the convolutional layers. Convolutional layers are the core building blocks of convolutional neural networks. And they operate by applying a filter to input to generate an activation. A feature map is the result of convolution between the kernel filter and the streamflow time series. Figure 4b depicts the model architecture and structure of the forecasting method. The CNN network layer and the fully connected layer make up the majority of the architecture (dense layer).
LSTM algorithm
Similar to the CNN, the long short-term memory (LSTM) is a neural network used in deep learning. The feedback connections employing the gating mechanism are the core working concept of the LSTM. These gates govern the information that enters and exits the memory cells, allowing crucial information to be preserved for as long as possible. Figure 4c shows the schematic diagram of LSTM layers.
Forest-based algorithms
An ensemble technique called a random forest (RF) uses a subset of events and a sample of parameters to establish a decision tree. It creates several of these decision trees and combines them to provide a more precise and reliable forecast. A gradient boosting machine (GBM), similar to the RF, is an ensemble approach by combining the results from several trees. One notable distinction is that the GBM constructs trees one at a time, with each new tree aiding in the correction of mistakes committed by the prior trained tree.
Performance evaluation metrics
For a regression-based problem, the root mean square error (RMSE), a measure of how accurate the model predicts the response (streamflow forecast), is thus a suitable metric to evaluate the performance of the algorithms. As for the categorical-based streamflow forecast, the model performance was further assessed using accuracy, precision, recall, and F-score measures. The mathematical definitions of the performance measures precision, recall, and F-score are defined in the equations below:
where \({\text{precision}}\) = percentage of results which are relevant, \({\text{recall}}\) = percentage of total relevant results correctly predicted by the algorithm, \({\text{TP}}\) = number of correctly predicted \(i\)th class of categorical streamflow forecast, \({\text{FP}}\) = outcomes where the predicted \(i\)th class of categorical streamflow forecast is wrong, \({\text{FN}}\) = number of incorrectly predicted \(i\)th class of categorical streamflow forecast. An N × N confusion matrix is used to evaluate the performance of a classification model, where N is the number of target classes. The matrix compares the actual target values to the machine learning model's forecasts.
Results and discussion
Performance analysis of hyperparameter optimization approaches
Bayesian optimization's performance should be evaluated in concurrence with other HPO strategies to establish whether Bayesian optimization is appropriate for working on optimizing the machine learning hyperparameter for streamflow forecasting. Two strategies: the Random search and the Hyperband, which are commonly known, including the Bayesian optimization, were statistically evaluated to obtain fair comparative results. Table 2 summarizes the results of ten independent runs conducted for each strategy. The evaluations were carried out using a computer outfitted with an i5-7400 T processor running at 2.40 GHz and 8 GB of RAM. Prior to analyzing the machine learning hyperparameter, this part serves as a preliminary section to discover the improved searchability of the HPO in this streamflow forecasting.
It is clear that the Bayesian optimization method outperforms the Random search and the Hyperband, whether the worst, best, or average, of the produced solutions. The findings of the Bayesian optimization demonstrated its effectiveness in tuning the hyperparameter of machine learning algorithms. It is the preferable approach since the total of the objective functions is better than the other strategies. Table 2 also shows the standard deviation of the overall solutions obtained for each strategy. The highest standard deviation (SD) obtained by the Hyperband among the chosen methods was 0.0144, approximately 29% higher than the SD (0.0112) produced by the Bayesian optimization. The low standard deviation of the Bayesian optimization demonstrates its excellent reliability for the task, as seen with the negligible differences between results produced from several runs of the Bayesian optimization.
Figure 5 depicts the convergence characteristics of the various hyperparameter optimization (HPO) techniques based on ten runs for the hyperparameter tuning procedure. The Bayesian optimization achieves a faster convergence rate than the Random search, whereas the Hyperband is the slowest. Aside from that, another advantage of the Bayesian optimization is that it can produce more accurate results than other strategies. According to Table 2, the Bayesian took an average of 74 iterations to converge, whereas the Random search required double the number of iterations to reach its local optimum. It is worth noting that the iteration rate in the Hyperband searching process is substantially greater (up to more than 400 iterations); however, the displayed range was standardized to a number iteration of 250 value for clarity purposes. In the case of the Hyperband, advancement is not only sluggish but it was also hard to find better solutions; improvement continues but gets less likely as time passes.
It is important to note that the convergence rate does not correspond to the computation run time. The Hyperband has a faster computational run time than the other two due to its random sampling configuration and iteratively generating the most promising one by emphasizing the better solution rather than poor configurations. However, a significant number of training epochs may be required for the machine learning algorithm to converge. When employing the Hyperband, some ideal configurations that may initially converge slowly will be removed early without reaching their best solution.
Statistical evaluation of the hyperparameter optimization (HPO)
The effectiveness of the HPO techniques may be assessed using any performance indicator; however, applying statistical tests can enhance the statistical analysis and comprehension of the HPO results. Despite these advantages, comparisons of the HPO performance and statistical data on their performance have not been published in the majority of situations. A statistical hypothesis test is a statistical inference procedure used to determine if the evidence at hand sufficiently supports a specific hypothesis. Non-parameter statistical tests are favored in this research (runs) due to the experiment's independent samples, implying that each algorithm's run is unique and there is no association between them.
The first statistical test was the Kruskal–Wallis H test, which computes the technique using data rankings rather than numerical values. The H statistical test may be mathematically stated as follows:
where N is the number of experimental runs, R represents the sum of ranking data for an algorithm, k represents the number of algorithms, and n represents the quantity of sorted data in an algorithm. The crucial value for rejecting the null hypothesis, according to Table 3, is 5.99, while the obtained value of H is 19.954. Since the critical value is less than H, the conclusion is to reject the null hypothesis. And the rejection of the null hypothesis demonstrates that the procedures used vary statistically.
As the Kruskal–Wallis test does not reveal the ranking of the HPO strategies, another statistical test such as the Mann–Whitney is necessary to supplement it. The U statistical test, like the preceding one, stresses the ranking in the data order. Following that, the ranking data are summarized in both approaches, respectively. The U statistical test may be computed as follows:
where
where m is the number of observations from the ith strategy. Table 4 displays the N × N matrix of the U statistical test findings. Among the strategies, the Bayesian optimization is regarded as the best compromise concerning the statistical test result tabulated in Table 4. Besides, due to their identical searching procedures, the Random search and Hyperband do not exhibit a substantial difference.
Pre-evaluation analysis
According to the details in the above section, the Bayesian optimization could tune the hyperparameter of a model without a precise formulation of the function through some approximation methods better than the selected approaches. Therefore, the Bayesian optimization technique was utilized to tune hyperparameters of three commonly used neural network algorithms with the objective delineated for each of the scenarios used in this paper. However, in order for the results to be plausible and valid, an efficient searching procedure for tuning the hyperparameters and their marginal importance in model performance was conducted and analyzed. Figure 6 depicts the overall flowchart of the work involved.
Bayesian hyperparameter tuning analysis
This section discusses the hyperparameter findings and their respective importance assessed by a Bayesian experiment. The search domain of the Bayesian optimization is outlined in Table 1 under section Machine learning algorithms and their hyperparameters. Figure 7 visualizes the progress of the optimization utilizing the expected improvement (EI) as the acquisition function based on the surrogate model after iteration to maximize the model's performance. The horizontal axis represents the iterations of the Bayesian optimization algorithm; the vertical axis represents the streamflow forecast performance metric. Based on Fig. 7, despite the search domain convergence rate for algorithms in each scenario varied from one another, it converged before reaching 200 iterations; therefore, the maximum iteration was set to 1000 for every experiment to be carried out. Setting an early termination rule, as previously described in section Bayesian optimization is preferred because overfitting can occur when the network size is large enough. The optimized values for the hyperparameters determined via Bayesian optimization are listed in Table 5.
To investigate how Bayesian optimization searches on the hyperparameter on the target response (streamflow forecast accuracy), an analysis of the plotting, as illustrated in Fig. 8, is required. That being the scenario, it allows one to obtain insight into the hyperparameter score sensitivity. The x-axis represents the hyperparameter value, while the y-axis represents model performance (predictive accuracy).
Learning rate
Taking the ANN as a reference (Fig. 8a), the range of which the Bayesian search for the hyperparameter ‘learning rate’ in scenario 3 was a typical low value, with values between 10–6 and 10–4 performing admirably; however, increasing the value to higher-order has a declining impact on model performance. In Scenario 1, the learning rate hyperparameter was reported to be about 10–2, which was two orders of magnitude greater than the average value of 10–4. In general, low learning rates, on average, need more training epochs, while high learning rates, on the other hand, will necessitate fewer training epochs.
Activation function
There is no trend in the distribution of the activation functions between tanh and sigmoid for each scenario, as shown in Fig. 8b. The tanh and sigmoid are functionally almost equivalent; therefore, there is not much of a difference between them. And it is evident in this study, that a comparative analysis on the selection between tanh and sigmoid is preferably carried out soonest, as they often vary according to the problem encountered. Similarly, the search domain for the activation function in the CNN and LSTM was the same as in the ANN. It should be noted that no ‘relu’ activation function was included in the search space for the LSTM since relu might have quite a few significant outputs, resulting in an explosive gradient.
Architecture network
Given the complexity of neural network algorithms, they resist formal analysis methods, which require an empirical approach. Therefore, there is no pre-defined size or architecture for an algorithm. Despite dealing with the identical problem, the hidden layer and number of neurons changed from one algorithm to another, as seen in this study (Fig. 8c). For example, the CNN worked best with five CNN layers, but the LSTM only required two LSTM layers. That is, neural networks are viewed as a multi-modal function optimization problem, demonstrating that several functions can give the same results.
Nevertheless, because the dependency plot is merely an assessment of the surrogate model, which is only an estimation of the underlying objective function that has been optimized, such interpretation of findings might be deceptive. In other words, the plots are a ‘guess of an estimate’ and may be highly inaccurate. Besides, the dependence plot does not indicate the impact of each hyperparameter has on model performance; hence, another approach for quantifying such findings was adopted, which is explained in detail in the next section.
Importance hyperparameter based on fANOVA analysis
Automated hyperparameter optimization (HPO) strategy can become inefficient when the neural network algorithms are trained until the end without early termination. The situation becomes worse when the algorithms are trained on unpromising hyperparameter configurations.
If the current hyperparameter setup isn't promising, it's preferable to cease training DNNs. In this way, the computation resource can be allocated to more promising settings. Furthermore, because the training cost of deep learning algorithms is typically higher than that of classic neural network algorithms in terms of time and computation cost, the tuning process has a much more significant influence on the performance of the algorithms. For this reason, in line with the Bayesian optimization, the functional Analysis of Variance (fANOVA) was considered in determining which hyperparameters have the most influence on the algorithm performance and therefore require the most tuning. The fANOVA analysis allows for the decomposition of performance variance, and the marginal importance of the algorithm hyperparameter may be estimated by aggregating their variance contributions over the model performance. Apart from that, the fANOVA analysis may be used to validate the partial dependency plots' results.
ANN results
The findings of the ANN scenario study are shown in Fig. 9a. The findings provide a clear insight: the number of neurons, time steps, and learning rate were the essential hyperparameters to govern all the scenarios. The ability to reveal a well-known ANN hyperparameter, such as the number of neurons, has proven that the proposed approaches are efficient. The choice of activation function, however, had the minimum influence on the ANN accuracy. In other words, utilizing the ‘sigmoid’ or ‘tanh’ activation function will have no impact on the accuracy of streamflow forecast via the ANN algorithm.
CNN results
Figure 8b illustrates the results of the convolution neural network, which revealed that only a few hyperparameters were found to be associated significantly with the overall model performance. It is worth mentioning that when utilizing the CNN, model complexity is critical, as seen in Fig. 9b, where the number of deep learning layers/nodes is rated in the top three for all scenarios. As Brigato and Iocchi (2021) had pointed out, one possible cause is that the deep learning technique requires more datasets to train (low samples per class). They demonstrated that when faced with sparse training samples and no data augmentation, low complexity CNN performs as well as or better than the state-of-the-art architectures. The results of another experiment employing the CNN algorithm, which uses images as input, are shown in Fig. 9c. The optimizer's hyperparameters, such as ‘number of time steps’ and ‘learning rate,’ appear to be just as essential as the size of the neuron in the CNN layer.
LSTM results
Figure 9d shows the results for the LSTM. There is a significant difference in the hyperparameter ‘number of time steps’ used in the categorical-based streamflow forecast compared to the regression-based streamflow forecast. Despite the fact that the values of the lag features are repeated, they are kept in vectors that may be independently weighted, allowing for unique contributions. In contrast to regression-based streamflow forecasting, the number of time steps has little influence on the categorical-based streamflow forecasting. Again, the activation function for all four scenarios, for all algorithms, was never the most crucial hyperparameter because computation time was not the criteria metric used to evaluate the algorithm performance. Activation functions are vital (as they introduce nonlinearity in the network), but which strategy to use for the algorithms does not matter much according to the four different scenarios.
Identifying the range of the hyperparameters
It is also interesting to examine whether there are any apparent optimal values across the various scenarios after choosing the significant hyperparameters. Figure 10 depicts the marginal plot for each algorithm's hyperparameters in different scenarios. The optimum learning rate values reveal that there is no ideal baseline across the scenarios, albeit, values between 10–4 and 10–2 perform well. The results of the ANOVA analysis also support this hypothesis, and the learning rate should be kept small. In addition, hyperparameters such as hidden layers, number of neurons, and activation functions in each algorithm vary from scenario to scenario. Therefore, hyperparameter tuning is essential to obtain good results. Last but not least, the impact of choosing the activation functions was significantly low compared to other hyperparameters. Several studies have found that the default relu activation function, for the ANN and the CNN, has a superior convergence speed and computational speed when compared to the sigmoid and the tanh. However, given that the computational speed is not subject to algorithm evaluation, thus, their impact was solely based on the model performance. If the evaluated activation function was at the last dense layer, then its impact could be significantly higher.
Categorical and regression analysis
Regression-based streamflow forecast
The residual analysis between the forecast and actual values of monthly streamflow, as shown in Fig. 11, was carried out to assess their model predictiveness. Residual analysis can reveal a lot of information that can be used to comprehend how the prediction model behaves. For example, Fig. 11 indicates that, while some residuals exceed the bounds, the majority of standardized residuals are within +−2, which means that there is no missing interaction in the data and that the time step chosen was sufficient. Besides, based on the autocorrelation function (ACF) of the residuals, given that all of the residuals were within the 95% confidence range, there was no association between them, indicating that the forecast values were unbiased despite their low predictiveness. However, a closer examination of the standardized residual versus the expected value reveals that all algorithms have a sign of heteroscedasticity, with the residual varying more as the projected value increases. When the residuals are heteroscedastic, the model's predictive ability varies depending on the data segment. The result demonstrated that high flow predictability is substantially poorer than in other regions, casting doubt on the models' suitability for flood forecasting applications, especially in flood-prone areas where peak flow is crucial. One possible explanation for such clear divergence could be the use of the MSE-based measures, which often accentuate mistakes in higher flows more than in lower flows, owing to heteroscedastic errors (Mizukami et al. 2019).
The regression-based streamflow forecast was assessed with a confusion matrix for a fair comparison with the categorical-based streamflow forecast. Compared to the scatterplot, the confusion matrix is more graphically informative by organizing streamflow data into specified intervals, which offers information about algorithm errors and the types of errors produced. Figure 12 shows the predicted–observed confusion matrix of the algorithms. The recall measure is represented by the percentage in the bottom row, whereas the right end column represents the precision score. The recall metric measures the number of the model correctly identifying the classified trend with respect to its own respective classified label. Meanwhile, the precision metric quantifies the number of correctly classified trends that belongs to the measured trend. The diagonal elements represent the number of correctly classified streamflow events and vice versa.
In scenario 1 for the ANN, the − Δ streamflow forecast had a recall score of 25% but with a precision of 71%, which means the model could only accurately identify the − Δ in the streamflow pattern for 17 out of 68 months. This is considered a poor performance, despite the high precision score. While all three algorithms could anticipate the + Δ streamflow change with a recall score ranging from 88 to 97%, the respective models only had precision of 0.5, which implies that they were only right 50% of the time when forecasting the streamflow would rise. Scenario 2 can be viewed as an extension of scenario 1. Even if the model can forecast when there was an increase in streamflow with a high recall (89%), closer investigation reveals that none of the increased streamflow forecasts could account for the sudden increases in streamflow value. It indicates that the model did not capture the transition from low to high. Intriguingly, as opposed to an increase in streamflow change, the model could detect the transition from low to high when the streamflow forecast was expected to decrease rather pretty well. The algorithm's performance on moderate and low changes in streamflow appeared to be satisfactory in most scenarios, with the CNN outperforming the ANN for subtle (low) changes in streamflow, and the ANN and LSTM outperforming the CNN for the moderate changes in streamflow.
In addition, two other classic and commonly used methods, the forest-based algorithms, namely, the random forest (RF) and the gradient boosting algorithm (GBM), were employed for such comparison. Given the study's relatively low-dimensional input data, classic forest-based algorithms may be far more efficient. According to Fig. 12, neither the GBM nor the RF could forecast + Δ changes in streamflow with higher precision than the neural network algorithms. The precision score of 0.71 obtained from GBM, the best outcome obtained by a forest-based algorithm, is only comparable to that of ANN, the least implicit neural network algorithm in regression-based univariant streamflow forecasting. Although the generalization of forest-based algorithms was higher since they could anticipate -Δ change in streamflow better, the improvement only appeared to be marginal. Additionally, scenario 2 analysis shows that forest-based algorithms behave similarly to neural network algorithms in terms of their inability to accurately detect the transition from low to high when streamflow is expected to increase. The lack of performance from machine learning algorithms in detecting the transition from low to high when streamflow is expected to increase would be evidence of the limitation of regression-based univariant streamflow forecasting.
Categorical-based streamflow forecast
In this section, instead of approaching the streamflow forecasting as a traditional regression machine learning using the MSE-based measure, the streamflow time series was evaluated as a categorical streamflow, which utilizes the categorical cross-entropy loss function with adjusted class weight for handling imbalance class. Table 6 shows the results and average values for the three neural network models and two forest-based models trained using tuned hyperparameter values. The comparative analysis has shown that there has been an overall improvement in all the scenarios considered using the five selected neural network algorithms, which indicates that the proposed method works efficiently. Although there was a trade-off between precision and recall scores for the CNN and LSTM, the higher f1-score illustrated an overall improvement. Another advantage of a categorical-based formulation is that the end outcomes were more evenly distributed result, as shown in Fig. 13. Forest-based algorithms, on the other hand, could at least have the ability to detect high streamflow variations better than neural network algorithms. It demonstrates that utilizing the proposed formulation of categorical-based streamflow prediction, a forest-based algorithm may be more appropriate for dealing with univariant streamflow forecasting, with improved performance. One probable reason for such results could be that neural networks will require much more data to be effective, unlike with RF.
Although the proposed categorical-based streamflow forecast has a substantial positive influence on the forest-based algorithms, recognizing a high shift in streamflow remains problematic with the neural network algorithms. Therefore, the encoded streamflow time series 2-D images were also conducted and analyzed to supplement its drawback. The streamflow dataset was transformed into an image-like representation based on several approaches, and the CNN was utilized due to its superiority in capturing the features from those images. According to Table 6, among the image transformation techniques, the RP performs the best, followed by the GAF and MTF, which are the worst. Neither the GAF nor the MTF is able to improve the performance. The disparity in model performance between the three methods suggests that using a transformed image to convert the streamflow time series may necessitate a thorough examination of the image transformation techniques, as evidenced by the decreased performance when using the GAF-based and MTF-based transformed streamflow.
Conclusions
This study evaluated the efficacy of different algorithms through the formulation of streamflow into two different machine learning problems. A comparative analysis of various hyperparameter optimization methods was performed. The results indicate that the Bayesian optimization is best suited to tuning the hyperparameters of machine learning in streamflow forecasting due to its rapid convergence to a better solution than other adopted HPO strategies. An analytical experiment study was also conducted using the fANOVA framework to determine the hyperparameters that are the most important for algorithms.
The findings also showed that the formation of a univariant streamflow forecast as a regression machine learning problem might be inappropriate due to the MSE-based approach, which could not account for the data imbalance issue. The residual analysis also showed that the low performance of these algorithms was not attributable to a lack of model capability but relatively to the data itself or the lack of predictors. When compared to regression-based streamflow forecasting, using the cross-entropy loss function with adjusted class weight in categorical streamflow forecasting, indicated an overall improvement in streamflow prediction accuracy. Among the selected algorithms, deep learning algorithms such as the CNN and the LSTM outperformed the ANN, for both formulated streamflow forecast problems. In comparison with the neural network algorithms, RF exhibits a significant improvement in streamflow forecasting from the regression-based to the categorical-based. Also, based on the fANOVA analysis, only a limited number of hyperparameters significantly affected the overall neural network algorithms performance. Furthermore, the optimal hyperparameters obtained through the Bayesian optimization were validated through the results of the ANOVA analysis. The identical results from both strategies suggest that the Bayesian optimization is very reliable when setting the algorithm hyperparameter in streamflow forecasting.
It should be emphasized that even with the deep learning algorithms CNN and LSTM, solving or addressing streamflow based on historical data solely has proven to be difficult, as indicated by the failure to address the sudden changes in streamflow in both the formulated problems. Concerning the problem of univariant streamflow forecasting, encoding the streamflow time series with image transformation, the series of features captured by the trained model has shown improvement in detecting the sudden change in streamflow than the counterfeit. Additional predictors, such as temperature, rainfall, and climatic indices, may be beneficial, but further research is required.
Data availability
The data that support the findings of this study can be obtained from the corresponding author upon request.
References
Balandat M, Karrer B, Jiang D, Daulton S, Letham B, Wilson AG, Bakshy E (2020) BoTorch: a framework for efficient Monte-Carlo Bayesian optimization. Adv Neural Inf Process Syst 33:21524–21538
Barra S, Carta SM, Corriga A, Podda AS, Recupero DR (2020) Deep learning and time series-to-image encoding for financial forecasting. IEEE/CAA J Autom Sin 7(3):683–692
Berman D, Buczak A, Chavis J, Corbett C (2019) A survey of deep learning methods for cyber security. Information 10(4):122
Brigato L, Iocchi L (2021) A close look at deep learning with small data. IEEE, pp 2490–2497
Bukhari AH, Raja MAZ, Sulaiman M, Islam S, Shoaib M, Kumam P (2020) Fractional neuro-sequential ARFIMA-LSTM for financial market forecasting. IEEE Access 8:71326–71338
Chaplot B (2021) Prediction of rainfall time series using soft computing techniques. Environ Monit Assess 193(11):1–11
Chen S, She R, Qin P, Kershenbaum A, Fernandez-Egea E, Nelder JR, Ma C, Lewis J, Wang C, Cardinal RN (2020) The medium-term impact of COVID-19 lockdown on referrals to Secondary Care Mental Health Services: a controlled interrupted time series study. Front Psychiatry 11:585915
Chong KL, Lai SH, Yao Y, Ahmed AN, Jaafar WZW, El-Shafie A (2020) Performance enhancement model for rainfall forecasting utilizing integrated wavelet-convolutional neural network. Water Resour Manag 34(8):2371–2387
Estebsari A, Rajabi R (2020) Single residential load forecasting using deep learning and image encoding techniques. Electronics 9(1):68
He M, Wu S, Kang C, Xu X, Liu X, Tang M, Huang B (2022) Can sampling techniques improve the performance of decomposition-based hydrological prediction models? Exploration of some comparative experiments. Appl Water Sci 12(8):175
Huang T, Chakraborty P, Sharma A (2021) Deep convolutional generative adversarial networks for traffic data imputation encoding time series as images. Int J Transp Sci Technol
Hutter F, Hoos H, Leyton-Brown K (2014) An efficient approach for assessing hyperparameter importance. In: Eric PX, Tony J (eds) PMLR, proceedings of machine learning research, pp 754–762
Jaquier N, Rozo L, Calinon S, Bürger M (2020) Bayesian optimization meets Riemannian manifolds in robot learning. In: Leslie Pack K, Danica K, Komei S (eds) PMLR, proceedings of machine learning research, pp 233–246
Kumar M, Kumar P, Kumar A, Elbeltagi A, Kuriqi A (2022) Modeling stage–discharge–sediment using support vector machine and artificial neural network coupled with wavelet transform. Appl Water Sci 12(5):87
Meddage P, Ekanayake I, Perera US, Azamathulla HM, Md Said MA, Rathnayake U (2022) Interpretation of machine-learning-based (black-box) wind pressure predictions for low-rise gable-roofed buildings using Shapley additive explanations (SHAP). Buildings 12(6):734
Mizukami N, Rakovec O, Newman AJ, Clark MP, Wood AW, Gupta HV, Kumar R (2019) On the choice of calibration metrics for “high-flow” estimation using hydrologic models. Hydrol Earth Syst Sci 23(6):2601–2614
Ndione DM, Sambou S, Kane S, Diatta S, Sane ML, Leye I (2020) Ensemble forecasting system for the management of the Senegal River discharge: application upstream the Manantali dam. Appl Water Sci 10(5):126
Pan B, Hsu K, AghaKouchak A, Sorooshian S (2019) Improving precipitation estimation using convolutional neural network. Water Resour Res 55(3):2301–2321
Pham BT, Luu C, Phong TV, Trinh PT, Shirzadi A, Renoud S, Asadi S, Le HV, von Meding J, Clague JJ (2021) Can deep learning algorithms outperform benchmark machine learning algorithms in flood susceptibility modeling? J Hydrol 592:125615
Probst P, Boulesteix A-L, Bischl B (2019) Tunability: importance of hyperparameters of machine learning algorithms. J Mach Learn Res 20(1):1934–1965
Rahman KU, Pham QB, Jadoon KZ, Shahid M, Kushwaha DP, Duan Z, Mohammadi B, Khedher KM, Anh DT (2022) Comparison of machine learning and process-based SWAT model in simulating streamflow in the Upper Indus Basin. Appl Water Sci 12(8):178
Ray S (2019) A quick review of machine learning algorithms. IEEE, pp 35–39
Reis GB, da Silva DD, Fernandes Filho EI, Moreira MC, Veloso GV, Fraga MS, Pinheiro SAR (2021) Effect of environmental covariable selection in the hydrological modeling using machine learning models to predict daily streamflow. J Environ Manag 290:112625
Ruiz AP, Flynn M, Large J, Middlehurst M, Bagnall A (2021) The great multivariate time series classification bake off: a review and experimental evaluation of recent algorithmic advances. Data Min Knowl Discov 35(2):401–449
Sagheer A, Kotb M (2019) Time series forecasting of petroleum production using deep LSTM recurrent networks. Neurocomputing 323:203–213
Schratz P, Muenchow J, Iturritxa E, Richter J, Brenning A (2019) Hyperparameter tuning and performance assessment of statistical and machine-learning algorithms using spatial data. Ecol Model 406:109–120
Shin S, Lee Y, Kim M, Park J, Lee S, Min K (2020) Deep neural network model with Bayesian hyperparameter optimization for prediction of NOx at transient conditions in a diesel engine. Eng Appl Artif Intell 94:103761
Sihag P, Singh B, Said MABM, Azamathulla HM (2021) Prediction of Manning’s coefficient of roughness for high-gradient streams using M5P. Water Supply 22(3):2707–2720
van Rijn JN, Hutter F (2018) Hyperparameter importance across datasets. Association for Computing Machinery, London, pp 2367–2376
Wäldchen J, Mäder P, Cooper N (2018) Machine learning for image based species identification. Methods Ecol Evol 9(11):2216–2225
Wang Z, Oates T (2015) Imaging time-series to improve classification and imputation
Zeinali M, Zamanzad-Ghavidel S, Mehri Y, Azamathulla HM (2021) Interaction of hydro-socio-technology-knowledge indicators in integrated water resources management using soft-computing techniques. Water Supply 21(1):470–491
Zhang B, Rajan R, Pineda L, Lambert N, Biedenkapp A, Chua K, Hutter F, Calandra R (2021) On the importance of hyperparameter optimization for model-based reinforcement learning. In: Arindam B, Kenji F (eds) PMLR, proceedings of machine learning research, pp 4015–4023
Zhu J-J, Sima NQ, Lu T, Menniti A, Schauer P, Ren ZJ (2022) Adaptive soft sensing of river flow prediction for wastewater treatment operation and risk management. Water Res 220:118714
Acknowledgements
This study was funded by Universiti Tunku Abdul Rahman (UTAR), Malaysia, via Project Research Assistantship and Post-doctoral Research Scholarship (Project Number: UTARRPS 6251/H03). The authors are grateful for the funding. The authors would like to express their gratitude to Malaysia's Department of Irrigation and Drainage (DID) for providing the streamflow data.
Funding
This study was funded by Universiti Tunku Abdul Rahman (UTAR), Malaysia, via Project Research Assistantship and Post-doctoral Research Scholarship (Project Number: UTARRPS 6251/H03). The authors are grateful for the funding. The authors would like to express their gratitude to Malaysia's Department of Irrigation and Drainage (DID) for providing the streamflow data.
Author information
Authors and Affiliations
Contributions
KLC contributed to conceptualization, methodology, formal analysis, software, writing—original draft, and writing—review and editing. YFH contributed to investigation, funding acquisition, supervision, project administration, and writing—review and editing. CHK contributed to visualization, validation, and supervision. MS contributed to methodology, validation, and writing—original draft. ANA contributed to methodology, resources, validation, and writing—review and editing. AE-S contributed to writing—original draft, visualization, validation, and supervision.
Corresponding author
Ethics declarations
Conflict of interest
The authors have no competing interests to declare that are relevant to the content of this article.
Ethical approval
This article does not contain any studies involving human participants or animals performed by any of the authors.
Informed consent
All of the authors have consented to submit the manuscript to Applied Water Sciences Journal.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Chong, K.L., Huang, Y.F., Koo, C.H. et al. Investigation of cross-entropy-based streamflow forecasting through an efficient interpretable automated search process. Appl Water Sci 13, 6 (2023). https://doi.org/10.1007/s13201-022-01790-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-022-01790-5