Introduction

Water is a very important part of human civilization; therefore, the contamination of water by industrial effluent is a great concern all over the world (Helmer et al. 1998; Lehr et al. 1980). To save water to save the world is the current slogan and to ensure a safer world for the future mankind is a great demand. The water crisis is increasing day by day. According to World Water Day, 2016 the water demand is increasing tremendously with the establishment of different industries, especially, heavy industries like textile, pharmaceuticals, leather, cosmetics, and agricultural sectors. Consequently, a huge amount of wastewater is generating from these industries and thronging them to the environmental water resources thus water pollution is occurring. It has been found that more than one lac types of dyes are commercially available and approximately 7 × 105 tons of wastewater is generated every year (Ozmen et al. 2008). Water can easily be polluted by dye molecules as a very small amount of dye can be detectable in open eyes (Robinson et al. 2001); therefore, discharged dyes are very harmful to the environment (Faur-brasquet et al. 2003). The dye is a mixture of various chemical compounds which used to color the fabric mainly in textile industries and cause serious water pollution whenever they are exposed to water (Garg et al. 2004). For example, methylene blue (MB) is commercially used as a dye, and water containing MB has many diverse effects on human, animals, and plants if they come in contact with each other. Therefore, the treatment of wastewater containing MB is an essential issue now a day. The existence of MB in environmental water resources affects the growth of plants as it hinders the photosynthetic rate in plants and it also origins various diseases in animals living in water kingdom (Taylor et al. 2015, 2013). Moreover, it causes many harmful diseases in the human body, for example, staining of skin, vomiting, nausea, bladder irritation, headache, fever, hypertension, etc. (Mokhlesi et al. 2003; Harvey and Keitt 1983).

Many methods are well known for industrial wastewater treatment like solvent extraction (Muthuraman 2011), membrane separation process (Seader and Henley 2011), electrochemical process (Bessegato et al. 2014), biological treatment (Almeida and Corso 2014), activated carbon (Emilia et al. 2014), oxidation (Doumic et al. 2014), etc.; however, most of these processes are complex and costly. In contrast, the adsorption (chemical or physical) process (Adebayo et al. 2014) is a worldwide recognized method for wastewater treatment as it is simple, cost-effective, prospective, and the adsorbents are abundant globally (Prola et al. 2013; Chen et al. 2013). Various types of low cost and effective adsorbents such as Mangifera indica seeds (Alencar et al. 2012), Nypa fruticans (Ali et al. 2016), coconut leaves (Jawad et al. 2016), tea dust (Khan et al. 2016), orange peels (Ángel et al. 2016), sawdust (Ál-husseiny, H. A. 2014), water hyacinth (Alam et al. 2015), Citrus limetta peels (Shakoor and Nasar 2016), mushroom substrate (Yan and Wang 2013), sugarcane bagasse (Zhang et al. 2013), banana peels (Amel et al. 2012), potato peels (Guechi and Hamdaoui 2016), stone olives (Hemsas et al. 2014), maize stem (Vučurović et al. 2014), palm kernel fiber (El-Sayed, G. O. 2011), pea shell (Khan et al. 2014), date palm leaves (Gouamid et al. 2013), etc., have already been developed to remove dyestuffs from industrial wastewater. Numerous factors like adsorption capacity and applicability, availability, cost-effectiveness, etc., should be considered during adsorbent selection. Considering this issue, the banana plant is selected as a locally available and inexpensive adsorbent to uptake MB from wastewater. The banana plant is a plant of the Musaceae family and its scientific name is Musa acuminate (Calvert 1990). The basic properties of the PBF are displayed in Table 1.

Table 1 Basic properties of banana fiber (Ferdus Alam 2021)
Full size table

In our recent study, the performance of the PBF adsorbent was investigated for the removal of MB from synthetic wastewater. Structural features of the adsorbent were studies and the process parameters were optimized. The equilibrium data were analyzed with Langmuir, Freundlich, Temkin, and Dubinin–Radgushkevich isotherms to find out the adsorption mechanism. The reaction kinetics was determined by the pseudo-first-order and second-order kinetic models. Intra-particle diffusion and mass transfer analyses including the adsorption mechanism of the PBF/MB system were carried out in the context.

Materials and methods

Preparation of adsorbent

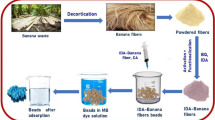
The adsorbent was prepared from low-cost and locally available materials. Banana fiber is a very cheap and locally available material and banana plants were collected from the local area of Jashore, Bangladesh. At first, the banana stems washed with DI water to separate dirt and unwanted parts. The clean stems are then cut into small pieces and wash again with DI water. The banana stem slices were then soaked for 40 min in a 40% solution of HCl and blended using a blender. The fiber was then separated by filtering the blended banana fiber. The filtered banana fiber was washed with DI water several times and dried at a certain temperature of 110 °C accordingly for 36 h. The as dried fiber was then ground and fine particles of 315–500 μm size were separated by using a sieve (Model: RETSCH, AS 200 Basic). The powder of the banana fiber was then stored in an air tight container to use as an adsorbent for the experiment.

Characterization of PBF adsorbent

Various techniques were carried out to analyze different characteristics of the PBF adsorbent. The functional groups of the adsorbent surface were detected by using an FTIR (FTIR 2000, Shimadzu, Kyoto, Japan). In this technique, approximately 2% of the sample was placed in 250 mg KBr disks to prepare the FTIR sample. The FTIR spectra were recorded in a range from 400 to 4000 cm−1 and with a resolution of 4 cm−1. The recorded FTIR spectra reveal the functional group present on the adsorbent surface. Additionally, the morphology of the banana fiber surface was investigated by using a Leo 435 VP scanning electron microscope (SEM). The porosity of the banana fiber surface was produced by SEM images of various magnifications at 5 kV.

Preparation of stock solution

Methylene Blue of analytical grade was collected from Merck, Germany. Adsorbate solution was prepared by dissolving a calculated amount of MB dye in DI water. This solution was used as a stock solution and experimental solutions were prepared by diluting this solution. For making the experiment at first 100 ml solution was prepared by dissolving 50 mg of MB in 500 ml of DI water. Additionally, solutions of different concentrations ranging from 25 to 300 were prepared for the experiment.

Batch adsorption study

Batch adsorption experiments were carried out to exemplify the adsorption performance of the PBF adsorbent to uptake the dye from synthetic wastewater at various operating conditions such as solution pH, initial dye concentration, and adsorbent dosage. The laboratory experiments were conducted at normal temperature and pressure. The required amount of adsorbents was taken in a conical flask containing as prepared 100 ml dye solution. The solution pH was adjusted by the inclusion of a calculated amount of 0.1 M NaOH or 0.1 M HCl. Afterward, 0.2 g of PBF was placed in the controlled pH solution and kept shaking for 12 h to reach the equilibrium. The adsorption was investigated using 100 ml of different dye concentrations (25–300 ppm) to understand the effect of solution concentration on adsorption. Additionally, the adsorption dosages effect was also examined by adding different dosages of PBF adsorbent (0.25–4.0 g) in 100 ml of dye solution of 100 ppm at constant pH 6 with a contact time of 12 h. The effect of contact time was determined by changing the time duration (10–300 min) of the adsorption process. In this process, 0.5 g of adsorbent was added in 100 ml of dye solution of 100 ppm at a pH 6. A UV visible spectrophotometer (HACH–DR–4000) was used at a wavelength of 666 nm to analyze the experimental solution after attaining the equilibrium concentration. The approximate dye removal percentage was computed using the given equation:

$$ {\text{MB Removal }}\% = \frac{{C_{o} - C_{t} }}{{C_{o} }} \times 100\% $$

where, Ct is the concentration of the MB solution at time, t and Co is the initial concentration of the dye solution. The quantity of dye adsorbed on the PBF adsorbent at equilibrium, qe (mg/g) is computed by the equation given below:

$$ q_{e} = \frac{{\left( {C_{0} - C_{e} } \right)V}}{W} $$

where, Ce is the concentration of dye solution at equilibrium (mg/l), W is the mass (g) of dry adsorbent, and V is the volume (l) of the dye solution.

Adsorption isotherm study

The information about the distribution of adsorbate molecules on the surface of the adsorbent can be found by the adsorption isotherm study. Generally, adsorption isotherm helps to correlate dye adsorbate present in the aqueous solution and the adsorption capacity of the adsorbent. Adsorption was carried out on banana fiber adsorbent at different solution concentrations from 25 to 300 ppm keeping other parameters (adsorbent dosage 0.5 g, pH 6, solution volume 100 ml, contact time 12 h) constant. Additionally, different models of adsorption isotherm like Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich were used to fit the adsorption data.

Langmuir isotherm

Langmuir adsorption isotherm model depicts that uniform adsorption occurs due to the homogenous distribution of energies through the surface and no transmigration takes place on the adsorbent surface amid adsorbates (Rotliwala et al. 2015). Langmuir adsorption isotherm equation can be expressed as follows:

$$ q_{e} = \frac{{Q_{o} K_{L} C_{e} }}{{1 + K_{L} C_{e} }} $$

The linear form of the Langmuir adsorption isotherm equation is as follows:

$$ \frac{1}{{q_{e} }} = \frac{1}{{Q_{0} }} + \frac{1}{{Q_{0} K_{L} C_{e} }} $$

where, Qo is the highest coverage of monolayer adsorption (mg/g), and KL is the isotherm constant (l/mg).

By plotting 1/qe versus 1/Ce a linear line was found; then the values of KL and Qo were calculated by the intercept and slope of the straight line. Langmuir isotherm model can be described in terms of a dimensionless constant, RL which is known as separation factor can be express as follows:

$$ R_{L} = \frac{1}{{1 + \left( {1 + K_{L} C_{0} } \right)}} $$

where, KL represents the adsorption constant related to the energy of the adsorption. The value of RL is very important for adsorption. If the RL value is higher than one (RL˃1), the adsorption is unfavorable. Similarly, if the RL value is equal to one (RL = 1), the adsorption likely to be linear; and if the value is less than one and higher than zero (1˃RL˃0), the adsorption is favorable (Rotliwala et al. 2015).

Freundlich isotherm

Freundlich adsorption model supports to describe the characteristics of the heterogeneous surface. This model can be written as follows:

$$ q_{e} = K_{f} \left( { C_{e} } \right)^{1/n} $$

where, n is the intensity of adsorption and Kf represents the isotherm constant (mg/g). The linear form of the isotherm model can be express as follows:

$$ \user2{ }log\,q_{e} = log\,K_{f} + \frac{1}{n}\,log\,C_{e} $$

where, 1/n defines the strength of adsorption. If the value of 1/n is one (1/n = 1), the partition between the two-phases is independent of concentration. Similarly, if the value is less than one (1/n˂1), it indicates normal adsorption and if the value is higher than one (1/n˃1), then cooperative adsorption takes place (Indhumathi and Saraswathy 2011).

Temkin isotherm

The interaction among adsorbate/adsorbent can be illustrated by the Temkin isotherm model. The equation of the isotherm model can be expressed as follows:

$$ q = \frac{RT}{b}\ln \left( {k_{T} C_{e} } \right) $$

The linear form of the above equation can be shown as follows:

$$ q_{e} = B\ln k_{T} + B\,ln\,C_{e} $$

where, B = (RT/b) is a constant associated with the heat of adsorption, R is the ideal gas constant (8.314 J/mol.K), b is a Temkin constant related to the heat of adsorption (kJ/mol), T is the temperature (K) and kT implies the Temkin equilibrium constant which is related to the binding energy (Bhattacharya et al. 2008a).

Dubinin–Radushkevich isotherm

Dubinin–Radushkeyich isotherm is an additional model for the adsorption of dye molecules on the adsorbent surface. The equation for Dubinin–Radushkeyich can be expressed as follows:

$$ q_{e} = q_{s } exp\left( { - B\varepsilon^{2} } \right) $$

where, \(\varepsilon \) can be defined by the following equation:

$$ \varepsilon = {\text{RT}}\ln \left( {1 + \frac{1}{{C_{e} }}} \right) $$

where, B is the adsorption constant, E represents the mean free energy. The energy, E can be calculated by the following equation when the MB molecules adsorbed on the PBF adsorbent surface from the bulk of the solution:

$$ E = \frac{1}{{\sqrt {2B} }} $$

Adsorption kinetics study

The adsorption kinetics of the process can be determined by a batch adsorption experiment. In this process calculated amount of adsorbent is added in a 100 ppm solution of MB. Whereas, the pH was maintained at 6 and the contact time changed from 10 to 300 min. The dye removal percentage was monitored after each batch experiment. The adsorption percentage was computed using the equation below:

$$ q_{e} = \frac{{\left( {C_{0} - C_{e} } \right)V}}{W} $$

where, the symbol qe indicates the quantity of dye adsorbed at equilibrium, V is the volume of the dye solution, Co is the initial solution concentration of dye and Ce is the dye solution concentration at equilibrium. W is the weight of the adsorbent in grams. Adsorption kinetics can be determined by using pseudo-first and second-order kinetics models.

Pseudo-first-order model

The adsorption rate constant can be measured by the pseudo-first-order kinetic model. The equation for the pseudo-first-order kinetic model is shown as (Bhattacharya et al. 2008a).

$$ {\text{log }}(q_{e} - q_{t} ) = {\text{log}}q_{e } {-}\frac{{k_{1} }}{2.303}t $$

where, qe represents the quantity of dye adsorbed at equilibrium and qt indicates the amount of adsorbate adsorbed after time t on the surface of the adsorbent. k1 indicates the adsorption kinetics rate constant (min−1). By plotting log(qe −  qt) versus t a linear line was found, the value of k1 is determined from the slope of the linear line (Bhattacharya et al. 2008a).

Pseudo-second-order model

The kinetics data can be analyzed by a pseudo-second-order model. The adsorption capacity is proportionally related to the surface active sites of the adsorbent. The equation for the pseudo-second-order kinetics model can be written as (Ho et al. 2000).

$$ \frac{t}{{q_{1} }} = \frac{1}{{k_{2} q_{e}^{2} }} + \frac{1}{{q_{e} }}t $$

where, k2 is the second-order kinetics constant. By plotting t/q1 versus t, a straight line was obtained and the value of qe and k2 (g mg−1 min−1) is obtained from the slope and intercept of the straight line.

Mass transfer analysis

The transfer of MB dye molecules (mass transfer) from the solution to the surface of the banana fiber powder was carried out by the equation of the Mckay et al. (1981),

$$ {\text{In}}\,\frac{{C_{t} }}{{C_{0} }} - \frac{1}{{1 + {\text{MK}}_{bq} }} = {\text{In}}\frac{{MK_{bq} }}{{1 + MK_{bq} }} - \frac{{1 + MK_{bq} }}{{MK_{bq} }}\beta S_{s} t $$

Where, β is the mass transfer coefficient. The value of β is determined from the slope of the individual plots of {(1 + MKbq)/MKbq)}βSs. Additionally, a graph was carried out by plotting ln{Ct/C0 − 1/(1 + MKbq)} versus t.

Intra-particle diffusion model

Various kinetics models were investigated, the interparticle diffusion model is the most important of them (Demirbas et al. 2004). The equation of Weber and Morris can be used to describe of interparticle diffusion mechanism (Weber and Carrell Morris 1963). The Weber and Morris rate equation can be expressed by the following equation:

$$ K_{id} = q_{t} /t^{1/2} $$

where, Kid represents the rate constant for intra-particle diffusion (mg/g min1/2). By plotting qt versus t1/2 a linear line is obtained the value of Kid can be measured from the slope of the straight line. If the line is not gone through the origin and the line is not linear then interparticle diffusion is not the only mechanism (Okoronkwo and Anwasi 2008). Interparticle diffusion was conducted in a 100 ml dye solution of 100 ppm where the contact time and pH of the solution were t1/2 and 6, respectively.

Results

Adsorbent characterizations

FTIR study of the adsorbent

FTIR analysis of the banana (Musa acuminata) pseudo-stem is indicative of molecular functional groups which demonstrate important characteristics of the fiber presented in Fig. 1. Abraham et al. (Abraham et al. 2011) discovered the major constituents of the PBF to be cellulose, hemicellulose, and lignin which are composed of alkanes, alcohols, aromatic ketones, and esters with various functional groups containing oxygen. The work enables to identify the nature of the chemical linkages.

Fig. 1
figure 1

FTIR spectrum of pseudo-stem banana fiber

Full size image

The absorption bands at 3750 and 3430 cm−1 are due to O–H groups and stretching vibration of O–H bonding. Ibrahim et al. (Ibrahim et al. 2010) reported that O–H stretching is related to absorbed alcohols which are common for all the constituents of the fiber. The characteristics of any natural fiber can be explained by C–H stretching and the absorption band observed at 3032 cm−1 for the current study. Moreover, the bands at 2380 and 2230 cm−1 are associated with the molecular linkages of the PBF.

Besides, the bands at nearby 1780 and 1670 cm−1 are related to C=O stretching attributed to acetyl or ester groups of the cellulose constituents. The spectrum exhibited strong bands at 1355 and 1215 cm−1 are due to C–H deformation and lignin. In fact, C–H and C–O deformation stand for ether linkages (Ibrahim 2002). The band exposed at 1135 cm−1 is due to dialkyl ether linkages of C–O–C symmetric stretching and C–O stretching vibration present in the key components of the PBF. A broad region of overlapping bands of absorption (2000–1400 cm−1) due to aromatic linkages of C–C, C = C, OH, CO, CHn, C–O–C, C–H. These features are characteristics of β − glycosidic linkages amid the repeating units of anhydroglucose present in cellulose.

SEM analysis

Surface morphology and basic physical properties of the PBF material are merely characterized by SEM. The SEM image of the banana powder is presented in Fig. 2. The Figure revealed the morphology of the pristine banana fiber that displays rough surface and the average diameter of the pores (approximately 1 µm) results in the better possibility to be trapped and adsorbed waste materials into these pores.

Fig. 2
figure 2

SEM spectrum of pseudo-stem banana fiber and original banana fiber (inset)

Full size image

The walls of the pores are composed of fibrils which are embedded in a uniform matrix (Lüttge et al. 1992). It has been proposed that fibrils are made of cellulose which constitutes the skeleton of cellular walls. They appeared rather in parallel arrangement point out the characteristics of the secondary wall of the plant (Fig. 2, inset) (Bilba et al. 2007). The homogenous matrix is conceivably a mixture of various lignin, polysaccharide acids, and hemicellulose as discoursed by FTIR.

Batch adsorption study

Effect of solution pH

pH is one of the most important parameters which affects the adsorption capacity of the adsorbate solution. MB dye removal was investigated over pH from 1 to 10 as a function of H+ concentration shown in Fig. 3. The optimum pH value was observed to be 6 for 55.91% dye removal. In fact, pH is associated with the mechanism of MB adsorption on the PBF adsorbent surface. The chemical formula of methylene blue is C16H18N3SCl, an aromatic compound with a heterocyclic structure. Two mechanisms of adsorption may be planned in such a way (i) chemical reaction between –OH on the PBF surface and Cl− in MB molecule results in dye removal through eliminating HCl in the system and (ii) electrostatic interaction amid protonated and deprotonated groups at the interface of PBF/MB system (Umoren et al. 2013). At pH ≤ 6, the PBF surface is protonated as follows:

$$ {\text{OH}}^{ - } + {\text{ H}}^{ + } \to {\text{ OH}}_{{2}}^{ + } $$
$$ {\text{OH}}_{{2}}^{ + } + {\text{ D}}^{ + } \to {\text{OH}}_{{2}}^{ + } \ldots {\text{ D}}^{ + } \left( {{\text{repulsion}}} \right) $$
Fig. 3
figure 3

Impact of solution pH on MB dye adsorption on PBF adsorbent surface at optimum conditions (MB concentration 100 ppm, adsorbent dosage 0.2 g/l, contact time 12 h)

Full size image

Adsorption decreases at pH ≤ 6 due to the cationic interaction of the dye molecule. Nevertheless, optimum pH was considered at pH 6 for MB removal of ⁓56% point out the fact that at this pH region a combination of Vander Waals Force and the formation of hydrogen bonding are predominant (Umoren et al. 2013). At pH˃6, adsorption gradually increased due to deprotonation of the adsorbent and ultimately released free O2 on the PBF surface. At this condition, the adsorption process ameliorated owing to electrostatic attraction with the cations as presented below:

$$ {\text{OH}}^{ - } \to {\text{ O}}^{ - } + {\text{ H}}^{ + } $$
$$ {\text{O}}^{ - } + {\text{ D}}^{ + } \to {\text{ O}}^{ - } \ldots {\text{D}}^{ + } \left( {{\text{attraction}}} \right) $$

Therefore, with increasing pH, adsorption for cationic dyes is enhanced as the surface sites of negatively charged on the PBF adsorbent are increased thanks to electrostatic attraction (Senthil Kumar et al. 2010). The adsorption capacity of the as-prepared PBF adsorbent is compared to some other low-cost adsorbents are listed in Table 2.

Table 2 Comparison of different low-cost adsorbents with removal percentage at operating pH
Full size table

Effect of adsorbent dosage

The effect of adsorbent dosage on MB uptake by PBF powder is displayed in Fig. 4. The removal efficiency of MB is somehow proportionally affected by various adsorbent dosages. With the increase of PBF adsorbent dosage from 0.25 to 1 g, the dye removal percentage also increased from 29.28 to 59.17%. If the adsorbent dosage is increased again from 1 to 4 g the removal percentage also increases simultaneously from 59.17 to 77.148% and after that the separation percentage becomes constant. The optimum adsorbent dosage of 1 g was obtained for the most favorable efficiency of MB dye removal. Active sites on the PBF adsorbent increased as the more active surface area is available for adsorption due to increasing adsorbent dosage. Banana fiber consists of lignin and cellulose-based plant materials of various active groups as discussed in spectrometric analysis and these functional groups take part in chemical bond formation with dye molecules present in the dye solution. With the increase of PBF adsorbent amount, there is a possibility to increase the separation of MB dye from the solution. The comparison of dye removal percentage of PBF with other low-cost adsorbents is displayed in Table 3.

Fig. 4
figure 4

Impact of PBF adsorbent dosage for MB dye removal from aqueous solution at optimum conditions (pH 6, MB concentration 100 ppm, contact time 12 h)

Full size image
Table 3 Comparison of the performance of PBF with different low-cost adsorbents regarding various adsorbent dosages
Full size table

Effect of initial dye concentration

The initial concentration of MB dye affected the separation efficiency of the adsorption process. The dye percentage of dye separation was decreasing with increasing concentration from 25 to 300 ppm, while the solution pH was fixed to 6, the contact time was maintained for 12 h and adsorbent dosage was constant to 1 g as shown in Fig. 5 because the adsorbent surface of PBF was saturated with the adsorption sites of MB. At lower concentrations, there are some unused active sites on the adsorbent surface and with increasing initial dye concentration; there will be a shortage of active sites for a fixed amount of adsorbent (Kannan and Sundaram 2001). The driving force required for mass transfer between aqueous (MB) and solid phases (PBF) is increased owing to higher MB concentration point out the possibility of higher molecular collision amid the active groups of the phases (Bulut and Aydın 2006). At low concentration, adsorption sites uptake solute molecules from the MB/PBF system more quickly as well as adsorption takes place at higher energy sites (Horsfall and Spiff 2005). On the contrary, at a higher concentration, the adsorption efficiency decreases as the higher energy sites become saturated and adsorption starts at the sites of lower energy. In this research work, the ideal concentration of the MB dye was found to be 100 ppm with a dye separation efficiency of 57.89%.

Fig. 5
figure 5

Impact of initial MB dye concentration on PBF adsorbent at optimum conditions (pH 6, PBF dose 1 g, contact time 12 h)

Full size image

The adsorbent activity of PBF at various dye concentrations can be compared with other low-cost adsorbents as displayed in Table 3. It has been found that the separation of methyl orange by chitosan/alumina at different concentrations of 20 to 400 ppm the dye removal percentage decreased from 99.53 to 83.55% (Zhang et al. 2012). Similarly, the separation of MB dye by pine leaves from aqueous solution decreased from 96.5 to 40.9% with the increase of solution concentration from 10 to 90 ppm (Yagub et al. 2012).

Effect of contact time

The contact time effect was investigated by adding 1 g of PBF adsorbent in 100 ml of dye solution with a concentration of 100 ppm at a constant pH of 6 as displayed in Fig. 6. The figure depicts that the increment of contact time from 10 to 300 min improves the MB dye separation percentage. Initially, the dye uptake activity was slower for 10 min. The variety of adsorbents and their reactive functional groups affect the adsorption kinetics of the system. The optimum for the adsorption of MB dye on the PBF adsorbent was found to be 100 min with a dye uptake capacity of around 47.63%. To consider the adsorption process of the clarified sludge/rice husk system, a contact time of 2 h was required to establish equilibrium. In the case of some other adsorbents, the physical properties of adsorption were conducted for a contact time of 2–5 h to confirm equilibrium conditions (Macedo et al. 2008).

Fig. 6
figure 6

Impact of contact time for the separation of MB dye on the surface of PBF at optimum conditions (pH 6, PBF dose 1 g, MB concentration 100 ppm)

Full size image

Adsorption isotherms

Adsorption isotherm is a vital parameter to analyze the adsorption data that helps to understand the adsorption mechanism of MB molecule on the PBF. Four adsorption isotherms of Langmuir, Freundlich, Temkin, and Dubinin–Radushkeyich models were used to fit the adsorption data of the MB/PBF system. Additionally, Table 4 describes the adsorption parameters obtained from the fittings of the isotherm models.

Table 4 Various adsorption isotherm parameters of MB dye adsorbed on PBF
Full size table

Langmuir adsorption isotherm

Langmuir isotherm indicates the monolayer adsorption mechanism of MB dye on the surface of the PBF. According to this isotherm model, only one layer of adsorption takes place and after the first layer of adsorption, no adsorbate is adsorbed on the adsorbent surface. The plot of 1/qe versus 1/Ce results in a linear line shown in Fig. 7 and the extracted values of the parameters are inserted in Table 4. The highest monolayer coverage (Q0) was computed from the intercept and slope of the linear fitting, respectively (Chakraborty et al. 2011). The adsorption capacity of the PBF (Qo) from the isotherm model was calculated as 42.28 mg/g, KL 2.27 l/mg and RL 4.386 × 10−3 results in favorable conditions for equilibrium sorption (Table 4). The value of R2 is 0.9979 which is very close to one indicating the better fitting of the isotherm model. According to this model, the MB adsorbate molecules are homogeneously distributed over the surface of the PBF and monolayer adsorption has been assumed. According to Fig. 7, the value of the separation factor, RL˃0 but RL˂1 designates that the adsorption isotherm is promising. In a nut shell, the Langmuir adsorption isotherm is the best fitted model (R2) as regards the data extracted from the fittings of the additional isotherm models.

Fig. 7
figure 7

Langmuir adsorption isotherm for the adsorption of MB dye on PBF surface

Full size image

Freundlich adsorption isotherm

According to the Freundlich isotherm model, both physisorption and chemisorption take place. In this model, first monolayer adsorption takes place and after that multilayer adsorption occurs through physisorption. The isotherm model is presented in Fig. 8 and the adsorption data are displayed in Table 4. The values of 1/n, n, Kf, and R2 were found to be 0.30, 3.33, 0.521 mg/g and 0.991, respectively. Freundlich adsorption constant n describes the adsorption mechanism and 1/n is the function of the adsorption strength. If the value of n is higher than one (n > 1), the adsorption is favorable and if the value is less than one (n˂1), the process is unfavorable (Chakraborty et al. 2011). Moreover, Kf is the adsorption constant which implies the indicator of adsorption capacity (Bentahar et al. 2016). Therefore, according to this model, heterogeneous adsorption is suspected.

Fig. 8
figure 8

Freundlich adsorption isotherm of MB dye adsorption on the PBF surface

Full size image

Temkin adsorption isotherm

By plotting qe versus lnCe, a linear line was obtained as displayed in Fig. 9. KT and B are the isotherm constants which were computed from the slope and intercept of the line. Here, KT is related to the binding energy and B corresponds to the heat of adsorption. It was found that the heat of adsorption is decreased during layer formation by the MB molecules on the surface of the PBF adsorbent due to the interaction between adsorbate and adsorbent substances (Bhattacharya et al. 2008a). The values of the isotherm constants (KT and B) and correlation factor (R2) are displayed in Table 4.

Fig. 9
figure 9

Temkin adsorption isotherm of MB dye adsorption on the PBF surface

Full size image

Dubinin–Radushkevich adsorption isotherm

Dubinin–Radushkeyich isotherm is also an important model for the fitting of adsorption data. In this isotherm model, a straight line was found by plotting lnqe versus ε2 (Fig. 10); the isotherm constants qs and E were then measured from the intercept and slope of the line, accordingly. The estimated values of the adsorption parameters are displayed in Table 4. Here, the qs cx represents the adsorption capacity, and the adsorption saturation point for MB on the banana fiber adsorbent was determined by this adsorption isotherm model. The value of E indicates the types of adsorption taking place, for instance, if the value is 8–16 kJ/mol chemical adsorption will occur; similarly, if the value is less than 8 kJ/mol physical adsorption will take place (Chowdhury and Saha 2010). In the current issue the value was found to be 10.19 kJ/mol results in indicating MB chemically adsorbed on the surface of the low-cost adsorbent.

Fig. 10
figure 10

Dubinin–Radhushkevich adsorption isotherm of MB dye adsorption on the PBF surface

Full size image

Adsorption kinetics

The kinetic property of a liquid/solid adsorption system is an essential parameter to measure the rate of adsorption. Lagergren pseudo-first-order and second-order models based on the adsorption kinetic data were evaluated at different initial concentrations. According to the first-order model, the adsorption rate is proportional to the first power of the concentration. The sorption capacity of the solid phase can be determined by the pseudo-second-order model. Similarly, this model reveals that chemisorption takes place between adsorbate and adsorbent which is the rate-determining step of this kind.

Lagergren pseudo-first-order

According to Fig. 11, a linear line was found by plotting log(qe − qt) versus t for the first-order kinetics, which helps to determine the rate constant k1 from the slope of the linear fitting. The linearity of the plot results in the mechanism of the first-order adsorption. The rate constant k1 value of the model was determined to be 8.7 × 103 (min−1) from the least square method for the MB/PBF system along with the correlation coefficient of R2 = 0.9964.

Fig. 11
figure 11

Pseudo-first-order kinetic model for the adsorption of MB dye on the PBF surface

Full size image

Pseudo-second-order

The plot of t/qe versus t of the pseudo-second-order kinetic equation demonstrates somehow a linear relationship point out the values of k2 and qe corresponding to the intercept and slope (Fig. 12). Rate constant k2 and the value of correlation coefficient (R2) were found to be 5.03 × 102 and 0.999, respectively. The values of R2 revealed the better fitting of the kinetic data compared to the first-order model to uptake MB from dye enriched water.

Fig. 12
figure 12

Pseudo-second-order kinetic model for the adsorption of MB dye on the PBF surface

Full size image

Mass transfer analysis

The mass transfer model of the MB/PBF system can be explained by the plot of ln[Ct/Co − 1/(1 + MKbq)] versus t showed a linear line (Fig. 13). Mass transfer coefficient β was graphically evaluated from the slope [(1 + MKbq/MKbq)βSs] of the plot and the value was found to be 1.45 × 103 (R2 = 0.9962) which point out that transporting velocity of MB dye from the bulk solution to the solid PBF surface is very fast. Similar phenomenon also reported elsewhere (Coconut tree bark as a potential low-cost adsorbent for the removal of methylene blue from wastewater 2019; Bhattacharya et al. 2008b).

Fig. 13
figure 13

Mass transfer plot for the MB dye adsorption on the PBF surface

Full size image

Weber and Morris intra-particle diffusion

Steps involved in the adsorption of MB by means of PBF powder include transportation of dye molecules from the bulk phase to the solid surface followed by diffusion of the solute molecules into the pores. This diffusion is generally known as a slow rate-determining process. The adsorption process for the MB/PBF system at a certain pH 6 and PBF dosage of 1.0 g did not show a linear relationship over the time period representing that more than one phenomenon are involved during the adsorption (Fig. 14). The intra-particle diffusion coefficient was determined from the slope of the plot q versus t1/2 and the value was obtained to be Kid = 0.42 mg g−1 min−1/2. After a certain time of diffusion, almost a linear relationship was observed from the figure but the curve did not go through the origin. The reason behind such characteristics is the boundary layer effect that draws attention toward the mechanism of MB adsorption on the PBF surface to be complex and intra-particle diffusion is also a contributor at the time of the rate-determining step. The surface sorption largely depends on the intercept and with the increase of the intercept, the surface sorption also increased. The intercept and diffusion coefficient values of the plot increase with an increase in the initial MB dye concentrations. In fact, the initial portion of the diffusion curve is attributed to mass transfer and the linear portion is related to intra-particle diffusion (Nipa et al. 2019). Parvin et al. studied intra-particle diffusion model for the MB dye adsorption by coconut tree bark, which points out that the adsorption process has boundary layer effect (Parvin et al. 2019).

Fig. 14
figure 14

Weber and Morris diffusion model for the separation of MB dye on PBF adsorbent surface

Full size image

Adsorption mechanism

It is very important to figure out the mechanism of the adsorption to remove MB dye from the aqueous solution to the adsorbent surface. The adsorption process can be described based on the chemistry of the PBF adsorbent surface. FTIR is a useful technique to observe the interaction among adsorbate molecules and active sites existing on the surface of the adsorbent (Ahmad et al. 2012). PBF is polysaccharides by nature containing lignin, cellulose, and hemicellulose with polyphenolic groups. The surface functional groups are possibly useful for bond formation with reactive adsorbate molecules over different mechanisms. Besides, FTIR of the PBF adsorbent revealed the reactive groups of C=O and OH are in abundance. The PBF adsorbent is made out of different materials like lignin, cellulose, and β cellulose with some minor compounds (oil, protein, starch, etc.) (Senthil Kumar et al. 2010). Oxygen-containing functional groups (C=O, –C–O–C– and OH) are existed in large in β cellulose and cellulose. However, lignin having polymerized structure is a complex compound, which contains an aromatic substance and functions as a cementing matrix. These binding elements then hold mutual contributions of β cellulose and cellulose units (Bulut and Aydın 2006). Different properties of the adsorbent like functional groups, pH, and size of the pore play vital roles in understanding the sorption mechanism. The as-produced PBF is acidic in nature (pH 5.61) owing to the functional groups of alcohols, phenolic hydroxide, ethers, carboxylic acid, etc. The chemisorption occurs through hydrogen bonding among OH groups of PBF surface and Cl−/N atoms of the MB dye. The MB adsorption on the PBF adsorbent surface might take place either by charge localization or by aromatic rings containing in the basic dye. These aromatic rings are oriented in horizontal or perpendicular to the surface. The adsorption by charge localization is occurred by the hydrogen bonding between the active site of the adsorbent surface and one of the –NH2 groups present in the dye molecules. The orientation of the aromatic rings in the dye molecules is possibly oriented in the horizontal axis and this type of bonding is formed by either electrostatic force or by hydrogen bonding through the resonance structure of the MB dye (Bulut and Aydın 2006). However, the key mechanism of the adsorption is the charged surface and electrostatic attraction amid the dye molecules. The expected mechanism for the adsorption of MB dye on PBH is displayed in Fig. 15. A similar adsorption mechanism has been reported by Rahman et. al (Alencar et al. 2012) where date palm fiber was used as an adsorbent to remove heavy metal (chromium-VI) from industrial wastewater.

Fig. 15
figure 15

Plausible adsorption mechanism for the separation of MB dye on the PBF surface

Full size image

Discussion

In this investigation, we optimized pH 6, MB concentration 100 ppm, PBF adsorbent dosages 1 g, and PBF/MB contact time for 100 min. The maximum dye removal percentage was found at pH 6. Dye concentration also manipulated the adsorption process and dye removal decreased with increasing the MB dye concentration. The initial concentration has been optimized at 100 ppm. Adsorbent doses are directly proportional to the dye removal and the optimum adsorbent dosage is 1 g. A kinetic study of the adsorption process was performed based on interaction time. In fact, with increasing interaction time, the dye removal efficiency rises and the optimized value of the time was obtained 100 min. The data well fitted with the pseudo-second-order kinetics model. The effect of the equilibrium concentration of MB removal was simulated by fitting the adsorption data in different adsorption isotherms. Table 5 represents the comparable adsorption performance of numerous low-cost adsorbents to remove dyes from industrial wastewater. It can be observed from the table that PBF adsorbent has a superior adsorption ability of 42.28 mg/g than the others extracted from the literature reviews. Therefore, banana fiber can be recognized as a potential low-cost adsorbent for the separation of organic dyes from wastewater.

Table 5 Comparison of different low-cost adsorbents based on MB dye adsorption capacity of PBF
Full size table

In addition, regeneration of the used adsorbent and adsorbate is massive important to make the process economically viable. In this context, at a higher acidic and basic environment, the electrostatic attraction between the dye and adsorbent is significantly lower; hence simple washing by highly acidic or basic pH solution could give recovery of the PBF adsorbent and the MB dye. Besides, chemical treatment or other regeneration methods (Momina and Isamil 2018) would be employed. In fact, regeneration method is very important for economic and environmental aspects. Nowadays, the new generation is rapidly switching toward bio-based clean energy resources (Alam et al. 2014) as well as piezoelectric power generation (Shawon et al. 2022) to overcome global energy crisis.

Conclusion

Banana fiber has been demonstrated in the current issue as a suitable adsorbent for the elimination of dyes from industrial wastewater. Different adsorption properties like initial concentration, pH, contact time, and adsorbent dosages of PBF/MB were optimized for the highest separation of the dye. The higher the concentration of the dye results in the lower percentage of the MB uptake from the aqueous solution, whereas, dye separation percentage can be enhanced by increasing the adsorption contact time and increasing the addition of adsorbent dosage. Moreover, adsorbent dosage in higher quantity ameliorates MB adsorption because of the greater number of active sites present in the system. A kinetic study of the adsorption process was conducted and it has been observed that the adsorption process followed the pseudo-second-order kinetics model. The equilibrium data of the dye removal was tailored by the adsorption isotherms of Langmuir, Freundlich, Temkin, and Dubinin–Radushkevich. The obtained results indicate that adsorption of MB dye on the surface of PBF involved the complex mechanism of adsorption and two distinct stages. The other two adsorption stages comprised of the diffusion of the dye molecules through the boundary layer because of the external mass transfer effect and the intra-particle diffusion which helps during rate-determining steps.