Introduction

Over the past few years, the damages of natural disasters have soared due to the increase in the frequency of severe climatic issues resulting from climate change across the globe. Natural disasters related to drought, rain, and flood are among the most significant causes of social and economic issues (Lee et al. 2017). The damages related to rain and flood could be prevented by analyzing hydrological data. Recording the observed data of hydrological phenomena and creating time series about them is useful in the establishment of a preliminary understanding concerning the management of rainfall and the prediction of future occurrences (Shah et al. 2020). The assumption that increasing the number of rain-gauge stations can reduce the error and increase the accuracy of illustrating the reality is almost justified. Nevertheless, increasing the number of stations is constrained by factors like—among others—cost and regional conditions, and the optimal placement of a minimum number of stations can produce highly reliable observational data (Kwon et al. 2020; Fanny et al. 2013). While design goals are among the main challenges in developing optimal networks, the information theory has made it possible to deal with such problems and consider the goals of network design by offering various indicators (Keum et al. 2017).

The entropy technique as a modern method of assessing the performance of rain-gauge networks has attracted a lot of attention for the latter purpose (Zhang and Singh 2015; Nazeri Tahroudi et al. 2019). The theory of entropy investigates the information provided by the existing stations and makes it possible to remove the surplus stations and add the ones required in other areas by taking a statistical-probabilistic stance concerning the stations that exist in the network, their recorded information, and the communication between the existing stations (Karimi Googhari and Khalifeh 2013). The technique did not attract a lot of attention until the first half of the twentieth century due to its conceptual and calculation challenges. However, Shanon (1948) conducted extensive studies on the implementation of the theory and introduced some unknown concepts related to it (Valipoor et al. 2020). Moreover, a lot of studies have been conducted in the field of assessing and designing monitoring systems for water resources according to the entropy theory. Chen et al. (2008) proposed a composite method consisting of geo-statistics and entropy to determine the optimal number and distribution of rain-gauge stations in the north of Taiwan. They implemented the Kriging method to interpolate the rates of rainfall observed in the new locations of the rain-gauges and the entropy method to find a sufficient number of rain-gauges so that they can represent monthly rainfall. Moreover, they ranked the stations in terms of importance by calculating the entropy of information transmission and the shared entropy. Keum et al. (2017) made a brief investigation on the entropy terms implemented in the design of water monitoring systems. Then, they classified the recent applications of entropy into four groups (including precipitation, streamflow and water level, water quality, and soil moisture and groundwater networks) and investigated them. Joo et al. (2019) investigated and redesigned a hydrometric station by implementing two objective functions (i.e., changes in entropy information and the importance of each station according to their priority) using the Euclidean distance. They showed that 8 stations can be implemented instead of 12 ones so that the combination of the selected stations could reflect both the changes of entropy information and the importance of each station. Recent hydrological studies have combined the entropy and copula, and an extended introduction to this can be found in Hao and Singh (2013) where two main ways of combining the two concepts have been discussed. A simple way is to combine the entropy and copula to extract the copula distribution function based on the Principle of Maximum Entropy (POME) or the Minimum Cross-entropy (Kong et al. 2015; Liu et al. 2017), while another way is to estimate mutual information using the copula function (Xu et al. 2018). Moreover, entropy-based multipurpose criteria have been developed to evaluate and optimize hydrometric networks, and the copula functions have been usually implemented in analyzing the hydrological frequency for modeling multivariate dependence structures (Li et al. 2019). Li et al. (2019) used the copula theory to develop an entropy for the optimization of the hydrometric network of Taihu basin in China. They found that the DETC can effectively rank stations according to their importance and combine the decision-making priorities concerning the information content and redundancy. They developed a Dual Entropy–Transinformation Criterion (DETC) to detect and prioritize the most important stations and optimize the nominated network. The best models were selected out of the three Archimedean copula functions (i.e., Gamble, Frank, and Clayton). The DETC was evaluated by the DEMO criterion and was compared with the Minimum Transinformation (MinT) index to optimize the network. The results showed that the DETC can effectively rank the stations according to their importance and combine the decision-making priorities concerning the information content and data redundancy. Kwon et al. (2020) compared the conditional and joint entropy techniques to optimize the rain-gauge networks in Daegu and Gyeongbuk in South Korea and compared the results using the RMSE criterion. They found that the conditional entropy was more convenient than the joint entropy technique. Moreover, they showed that the rain-gauge stations were more predisposed to environmental rain-gauges. First, the stations were selected, and the central stations were added later. The efficient management of river basins requires that sufficient data related to rainfall are recorded so that the necessary managerial arrangements can be implemented after modeling and prediction. The quality of the data may be reduced due to irrelevant, insufficient, and inefficient data obtained from inconvenient locations, and this can influence the accuracy of the estimates. Thus, it is not acceptable that more data can better illustrate realities and overcome the limitations and problems that arise from data insufficiency. On the other hand, the lack of standard procedures to design optimal rain-gauge stations, the costs of adding new stations, and regional constraints limit the achievement of the intended goals. Thus, rating the existing stations, finding a convenient location for each station, and determining a sufficient number of stations to establish a network of rain-gauge monitoring are necessary to attain the goals of water resource management at the level of basins. While similar studies have implemented the multivariate regression analysis to investigate the interaction effects of the sites, the present study considered the statistical distribution of the data and the copula-based simulation to investigate the interaction effects.

Materials and methods

The investigated area

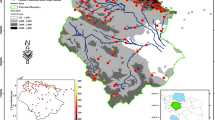
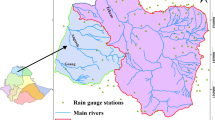
Tazehkand sub-basin is among the sub-basins of Siminehrood River around Lake Urmia in Northwestern Iran. Siminehrood is 200 km long, and its basin covered by the Tazehkand station is almost 3173km2. Its discharge is 9.67 l/s. Figure 1 illustrates the locations of the investigated rain-gauge stations in Tazehkand sub-basin. The present study implemented the annual rainfall data obtained from the rain-gauge stations in Tazehkand sub-basin the southwest of Lake Urmia during the 1981 to 2019 period. The sub-basin has 5 rain-gauge stations with adequate length and data whose statistical characteristics are given in Table 1.

Fig. 1
figure 1

The geographical location of Tazehkand sub-basin, Northwestern Iran

Full size image
Table 1 The statistical characteristics of the investigated stations
Full size table

The theory of entropy

Entropy means chaos; in other words, as the chaos of a system is higher, it means its entropy is higher. According to Shanon’s definition, for the two variables x and y where xi, i = 1,2,3, …, n and yi, j = 1,2,3, …, m on the same probability space, each one will have the occurrence probability of p(xi)، p(xi, yj) and the co-occurrence probability of xi، yj and p(xi│yj). The overall state of entropy is as follows:

$$ E(I(x) = H(x) = - \sum\limits_{i = 1}^{\infty } {p(x_{i} )} \ln p(x_{i} ) $$
(1)

where E(I(x)) indicates the expected value of the data. Indeed, according to the definition, the mean of the data (I(x) mean) has been implemented as a measure of uncertainty. The joint entropy indicates the data that exist both in x and y.

$$ H(x,y) = - \sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {p(x_{i} ,y_{j} )\ln p(x_{i} ,y_{j} )} } $$
(2)

For the two random variables x and y, the conditional entropy indicates the data in x that do not exist in y (Mogheir and Singh 2003).

$$ H(x\left| y \right.) = - \sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {p(x_{i} \left| {y_{j} } \right.)\ln p(x_{i} \left| {y_{j} } \right.)} } $$
(3)

It has been interpreted as a reduction in uncertainty in x based on an awareness concerning the random variable y. Moreover, it can be defined as the information related to x that exists in y (Lubbe 1996).

$$ T(x,y) = - \sum\limits_{i = 1}^{\infty } {\sum\limits_{j = 1}^{\infty } {p(x_{i} ,y_{j} )\ln \left( {\frac{{p(x_{i} ,y_{j} )}}{{p(x_{i} )p(y_{j} )}}} \right)} } $$
(4)

In the above equations, p(x) is the probability for the occurrence of x, p(x,y) is the probability for the joint occurrence of x and y, and p(x│y) is the probability of the occurrence of x dependent on y (Jessop 1995). It should be noted that T(x,y) = T(y,x) can be calculated using the following ways, as well:

$$ T(x,y) = H(x) - H(x\left| {y)} \right. $$
(5)
$$ T(x,y) = H(x) + H(y) - H(x,y) $$
(6)
$$ T(y,x) = H(y) - H(y\left| {x)} \right. $$
(7)
$$ T(y,x) = H(y) + H(x) - H(y,x) $$
(8)

Information transfer can also be expressed using a normalized Information Transfer Index (ITI), which indicates the amount of standard information transferred from one place to another. The classification of the rate of information transfer is given in Table 2.

$$ {\text{ITI}} = \frac{T(x,y)}{{H(x,y)}} $$
(9)
Table 2 A classification of the values of the ITI
Full size table

The information received by x from y can be defined in the following manner in terms of entropy:

$$ R(x,y) = \frac{T(x,y)}{{H(x)}} $$
(10)

It can be expressed as a reduction in the uncertainty of when y is known; in other words, it is a measure of the rate of the information received by well ‘x’ from well ‘y’. Like the information sent from x to y, it can be defined in the following manner:

$$ S(x,y) = \frac{T(x,y)}{{H(y)}} $$
(11)

The above equations express the relationships between the two variables x and y. The same argument can be implemented for each station using Eqs. (10) and (11). Moreover, the information sent and received by the ith station can be defined in the following manner:

$$ R(i) = R(x(i),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{x} (i)) $$
(12)

X(i) expresses the data of the ith station and \(\hat{x}(i)\) refers to the data estimate of the value of x(i). The latter is typically obtained using linear regression, though the copula-based simulation was implemented in the present study.

The higher values of R(i) and S(i) indicate the more significant received and sent information between the ith station or other stations in the network, respectively. In other words, they are measures of the more efficient communications between the stations.

In this way, the higher values of R(i) and S(i) for a particular station indicate the higher value of the station, and it is recommended to maintain and preserve such stations. On the other hand, the N(i) index or the ‘net exchanged information’ is defined in the following manner:

$$ N(i) = S(i) - R(i) $$
(13)

The N(i) index is important as it is used to assess the value of each station. It expresses the total net information of each well, and the station with the lowest N(i) index is assigned the lowest rank and importance in the monitoring network (Markus et al. 2003).

Investigating the interaction effects of the stations using copula functions

Vine copulas make different forms of dependence possible in various pairs and can easily model higher dimensions—e.g., 10 times—(Tahroudi et al. 2020a). The D-vine and C-vine copulas are the typical tree types. In a C-vine tree, dependence is modeled by bivariate copulas for each pair according to a particular variable (as the first root node). Thus, the dependencies of other pairs are selected according to the second variable (also called the second root node). In general, a root node is selected for each tree, and all pair dependencies are modeled according to this node and performed based on all previous root nodes. The R-Vine copula is more flexible than the C or D types as it provides a more extensive spectrum of structures. Figure 2 is a schematic representation of a 7-dimensional R-Vine copula. For instance, the pairs (1,2), (2,3), (3,4), (5,2), 3,6), and (6,7) are estimated at the first level of the 7-dimensional tree. On the other hand, the second level contains pairs like—among others—(1,2), (1,3|2), (2,6|3), (3,7|6), (3,5|2), and (2,4|3). The selection of copulas in lower levels has a significant effect on the conditional copulas of upper levels. Thus, the selection of copula families influences the other families.

Fig. 2
figure 2

A sample of the seven-dimensional R-Vine copula (Dißmanna et al. 2013)

Full size image

Assume that (x1,…xd) is a set of variables with joint distribution F and density f. Its structure is considered as follows:

$$ f(x_{1} ,...,x_{d} ) = f(\left. {x_{d} } \right|x_{1} ,...,x_{d - 1} )f(x_{1} ,...,x_{d - 1} ) = \cdots = \prod\limits_{t = 2}^{d} {f(\left. {x_{t} } \right|x_{1} ,...,x_{t - 1} )f(x_{1} )} $$
(14)

where F(·|·) and f(·|·) indicate the CFD and conditional density, respectively. As the second element, Sklar’s theorem for the d = 2 dimensions is as follows:

$$ f(x_{1} ,x_{2} ) = c_{12} (F_{1} (x_{1} ),F_{2} (x_{2} )).f_{1} (x_{1} ) = f_{1} (x_{1} ).f_{2} (x_{2} ) $$
(15)

where c12 (·,·) indicates the bivariate optional copula density. Using the above equation, it can be stated that the conditional density X1 considering X2 can be obtained as follows (Aas et al. 2007):

$$ f(\left. {x_{1} } \right|x_{2} ) = c_{12} (F_{1} (x_{1} ),F_{2} (x_{2} )).f_{1} (x_{1} ) $$
(16)

The following can be expressed for the distinct values i, j, i1,···,ik with i < j and i1 < ··· < ik:

$$ \left. {c_{i,j} } \right|i_{1} ,...,i_{k} : = \left. {c_{i,j} } \right|i_{1} ,...,i_{k} (F_{{}} (\left. {x_{i} } \right|x_{{i_{1} }} ,...,x_{{i_{k} }} ),F_{{}} (\left. {x_{j} } \right|x_{{i_{1} }} ,...,x_{{i_{k} }} )) $$
(17)

Using Eq. 16 for the conditional distribution (Xt, X1) considering X2,…, Xt−1, f(xt|x1,···, xt−1) can be expressed as follows:

$$ f(\left. {x_{t} } \right|x_{1} ,...,x_{t - 1} ) = c_{{\left. {1,t} \right|2,...,t - 1}} .f(\left. {x_{t} } \right|x_{2} ,...,x_{t - 1} ) = \left[ {\prod\limits_{s = 1}^{t - 2} {c_{{\left. {s,t} \right|s + 1,...,t - 1}} ].c_{(t - 1),t} .f_{t} (\left. {x_{t} } \right|)} } \right] $$
(18)

Implementing the above equation in Eq. 14 and s = i, t = i + j, the following can be obtained (Aas et al. 2007):

$$ \begin{aligned} f(x_{1} ,...,x_{d} ) & = \left[ {\prod\limits_{t = 2}^{d} {\prod\limits_{s = 1}^{t - 2} {c_{{\left. {s,t} \right|s + 1,...,t - 1}} } } } \right]\left[ {\prod\limits_{t = 2}^{d} {c_{(t - 1),t} ][\prod\limits_{k = 1}^{d} {f_{k} (x_{k} )} } } \right] \\ & = \left[ {\prod\limits_{j = 1}^{d - 1} {\prod\limits_{i = 1}^{d - j} {c_{{\left. {i,(i + j)} \right|(i + 1),...,(i + j - 1)}} .} } } \right]\left[ {\prod\limits_{k = 1}^{d} {f_{k} (x_{k} )} } \right] \\ \end{aligned} $$
(19)

The decomposition of the copula density consisting of the copula densities ci, j|i1,···,ik(·,·) is performed using the distribution function F(xi|xi1,…,xik) and F(xj|xi1,…,xik) for the specified indicators i, j,i1,…,ikand the marginal densities fk. It is for this reason that such an air-copula division is performed. Such a classification was called the D-vine copula by Bedford and Cooke (2001). There is a second class of analysis. When Eq. 16 with the condition distribution X1, Xt−2, (Xt−1) is considered, the following relationships can be developed:

$$ f(\left. {x_{t} } \right|x_{1} ,...,x_{t - 1} ) = c_{{\left. {1,t} \right|1,...,t - 2}} .f(\left. {x_{t} } \right|x_{1} ,...,x_{t - 2} ) $$
(20)

Using Eq. (20) instead of Eq. (18) in Eq. (14) and considering j = t − k, j + i = t, the following results are obtained:

$$ \begin{aligned} f(x_{1} ,...,x_{d} ) & = f_{{}} (x_{1} )\left[ {\prod\limits_{t = 2}^{d} {\prod\limits_{k = 1}^{t - 1} {c_{{\left. {t - k,t} \right|1,...,t - k - 1}} .f_{{}} (x_{t} )} } } \right] \\ & = \left[ {\prod\limits_{t = 2}^{d} {\prod\limits_{k = 1}^{t - 1} {c_{{\left. {t - k,t} \right|1,...,t - k - 1}} } } } \right]\left[ {\prod\limits_{k = 1}^{d} {f_{k} (x_{k} )} } \right] \\ & = [\prod\limits_{j = 1}^{d - 1} {\prod\limits_{i = 1}^{d - j} {c_{{\left. {j - j + i} \right|1,...,j - 1}} ].\left[\prod\limits_{k = 1}^{d} {f_{k} (x_{k} )}\right ].} } \\ \end{aligned} $$
(21)

According to Bedford and Cooke (2001), this pair-copula construction (PCC) is called the canonical vine or the C-vine.

The error estimation statistics

The present study implemented the root-mean-square error (RMSE), Akaike information criterion (AIC), and the Nash–Sutcliffe (NSE) statistics (Zhang and Singh 2006; Ma and Sun 2011).

$$ {\text{RMSE}} = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {(p_{ei} - p_{i} )^{2} } } $$
(22)

AIC values corresponding to maximum likelihood can be calculated using the following equation:

$$ {\text{AIC}} = 2m - 2\ln (L) $$
(23)
$$ {\text{BIC}} = N\,\ln \left( {\frac{1}{N}\sum\limits_{i = 1}^{N} {(p_{ei} - p_{i} )^{2} } } \right) + m\,\ln (N) $$
(24)

where, Pei and Pi are empirical and theoretical probabilities, respectively; N is number of data; m is the number of parameters and L is the maximum likelihood function value for the model.

Results and discussion

The present study implemented the rain-gauge stations in the Siminehrood Basin in Northwestern Iran during the 1981–2019 period. Six rain-gauge stations were implemented, and the characteristics of the stations are given in Table. As was mentioned before, multivariate regression was implemented to investigate the interaction effects of the sites. In the present study, the interaction effects of the stations were investigated by considering the statistical distribution of the data and the copula-based simulation. The first stage in the copula-based simulation was to investigate the correlation between the variables of the study using Kendall’s Tau statistic as it is the basis of the copula-based research studies. The results of investigating Kendall’s Tau are given in Fig. 3. Thus, the results showed that a significant correlation existed between the total annual rainfall values of the investigated stations. Thus, the preliminary and main conditions of the simulation and the investigation of the copula functions were fulfilled. The most significant correlation was observed in the Dashband-Ghezel Gonbad pair (0.79), while the least significant correlation was observed in the Rahimkhan-Tazehkand pair (0.37). Moreover, an average correlation of 0.52 was observed between all pairs of the variables.

Fig. 3
figure 3

The correlation between the annual rainfall records of the stations using Kendall’s Tau coefficient

Full size image

Investigating the tree structure of the investigated variable pairs

After confirming the correlations between the observed values, the R-family copula functions, and their tree structures were investigated. In this regard, various types of copula functions related to the family including the C, D, and R-vine, and their dependent and independent modes were investigated. The results of the best tree structures of the investigated copula functions according to the AIC and BIC criteria are given in Table 3. Furthermore, the tree structures of the best copulas are given in Table 4 and Fig. 4. According to Table 3 and the AIC and Log-Likelihood criteria, it can be observed that the R-Vine and R-Vine Independent showed similar performance according to the AIC criterion. On the other hand, the Log-Likelihood showed that the R-Vine was the best copula to investigate and simulate the 6-variable values of the annual rainfall in the studied stations. Moreover, the D-Vine got the lowest rank according to the investigated vines as it was assigned with the lowest value by the Log-Likelihood. Though selecting the R-Vine copula increased calculation complexities due to its extensive tree structure, it increases the accuracy of simulation and modeling.

Table 3 The tree structures of the various copulas belonging to the Vine family
Full size table
Table 4 The tree structure of the best copula
Full size table
Fig. 4
figure 4

The tree structure of the best copula

Full size image

Finally, investigating the Vine-family copula functions during the multivariate simulation of the total rainfall values considering the annual rainfall values of other stations in the Siminehrood basin showed that the R-Vine copula had the highest fit with the investigated variables, and it was introduced as the best copula compared to other according to the offered tree structure. Table 4 shows that 54% of the internal copulas were rotary. Due to the application of rotary copulas in the complete coverage of dependency directions, implementing them can increase the accuracy and performance of modeling.

Figure 4 shows that the R-vine had the best tree structure among the vine-family copulas. The figure illustrates the tree structure in six dimensions. The structure consists of five trees that show the connection modes of various parameters and their conditional states.

Numbers 1 to 6 indicate the rainfall values recorded in Dashband, Ghezel Gonbad, Kavlan, Tezahkand, Rahimabad, and Norouzlou stations, respectively (Fig. 4).

Copula-based simulation

After determining the best vine, its tree structures, and the internal copulas, the h-function and the probability density function of the copula functions were used to simultaneously simulate the annual rainfall values of the investigated stations according to the copula-based model. The simulation was multivariate, and the lack of rainfall in all stations was also taken into account. The correlations between the simulations and observations were investigated. In Fig. 5, the red numbers and shapes indicate the observational data, while the black ones are the simulated information. The results showed a significant correlation between the simulated rainfall values across the investigated stations. In most cases, the simulated values for various stations had higher correlations compared to the observational mode, and this showed the Vine simulation approach was a convenient way to simulate the annual rainfall values in the stations. Moreover, the convenient distribution and fit of the observed and simulated values were confirmed in all stations. The accuracy of the simulation procedure is given in Table 5. As can be seen in the table, the accuracy and efficiency of the Vine simulation approach were confirmed.

Fig. 5
figure 5

The correlation between the observed and simulated annual rainfall values of the stations (red: observed data; black, simulated data)

Full size image
Table 5 Estimates of the RMSE and NSE statistics in simulating the total annual rainfall of the investigated stations
Full size table

In Table 5, the error rate and efficiency of the model in simulating the multivariate values of annual rainfall are provided by the RMSE and NSE statistics, respectively. It can be observed the efficiency of the Vine simulation approach in all stations was above 92%. Moreover, the error rates ranged between 20.93 and 20.75 mm. Table 5 also illustrates the simulated values for the annual rainfall of the investigated stations in the Tazehkand sub-basin using the multivariate regression technique. As was mentioned above, multivariate regression is the typical method in the theory of entropy to investigate the interaction effects of stations. The results of comparing the RMSE values in the multivariate regression and the Vine simulation approach showed that the RMSE values obtained for the Dashband,Ghezel Gonbad, Kavlan, Tazehkand, Rahimabad, and Norouzlou stations improved by almost 41, 52, 80, 54, and 41%, respectively. Moreover, the improved rates of performance for the above stations according to the NSE measure were around 4, 8, 78, 33, 16, and 19%, respectively. In addition to the excellence of the Vine-based simulation technique according to the error statistics, the approach indicated higher certainty in simulation as it implemented a convenient marginal distribution with each time series and joint analysis (Table 6). Figure 6 shows the violin plot of the observed and simulated values concerning the annual rainfall of the investigated stations. Figure 6 indicates a complete fit between the observed and simulated values for the annual rainfall recorded in Dashband, Ghzel Gonbad, Kavlan, and Norouzlou stations. Though some underestimation can be observed in the case of Tazehkand station, the observed and simulated values have a convenient fit in terms of their variations. Moreover, the observed and simulated values for Rahimabad station were not fully fit. The figure indicates the efficiency and certainty of the Vine simulation approach in investigating the interaction effects of the rain-gauge stations in Tazehkand basin.

Table 6 The estimates of the ITI index for the rain-gauge monitoring network in the Siminehrood basin
Full size table
Fig. 6
figure 6

The violin plot of the variations between the simulated and observed values of the total annual rainfall of the investigated stations according to the 6-variable Vine simulation method

Full size image

After the accuracy and performance of the Vine simulation approach in investigating the interaction effects of the rain-gauge stations were confirmed, the entropy theory was implemented to estimate the ITI and N(i) indicators. The results of investigating the area in terms of the ITI index are given in Table 6, and the rating of the investigated stations is given in Table 7.

Table 7 The results of the N(i) index concerning the rating of the rain-gauge stations in the Siminehrood basin
Full size table

The results of the ITI index (Table 6) in the investigated area showed that Norouzlou station was average in terms of transferring rainfall information, Dashband and Ghezel Gonbad stations were in the surplus mode, and the remaining stations were above average. In general, no shortage of rain-gauge stations was observed in the investigated area concerning the rain-gauge monitoring network. In other words, the best monitoring could be achieved in terms of the rainfall data using the available stations in the region. Monitoring rain-gauge networks in each area or basin can provide accurate information about the spatial and temporal variations in rainfall values, and this is essential due to the climate change and the rainfall variations observed over the past few decades. Iran is located on the global dry belt, and recent droughts have had devastating impacts on it. This has been pointed out in many studies like Khalili et al. (2016), Khozeymehnezhad and Tahroudi (2019), Ramezani et al. (2019), Tahroudi et al. (2019a, b, c), and Tahroudi et al. (2020a, b). Understanding variations in rainfall and monitoring rain-gauge networks can have outstanding effects on the management of basins. Another important index in monitoring the rain-gauge networks is N(i) given in Table 7. Marcus et al. (2003) argued that the station with positive values of the N(i) should be maintained. Implementing the N(i) index to estimate the worth of each station and rank the investigated stations showed that Norouzlou station ranked last. This showed that the station sent and received less information compared to other stations in the network. Moreover, it was shown that the station had weaker communications with other stations. On the other hand, Dashband station ranked first, which showed its superiority in the investigated area. If a station is supposed to be eliminated, it is advisable to select the stations with lower ranks and negative N(i) values. Moreover, if a station is supposed to be introduced as the base station in the investigated area, Dashband station is the best choice. That is because the information provided by the station can be a convenient representation of the area in terms of rain-gauge information exchange. In general, the results of the entropy index offer accurate and all-inclusive information concerning the monitoring network of any area. Tahroudi et al. (2019a, b, c) confirmed the accuracy of the entropy theory in improving the monitoring network. Implementing all indicators of the entropy theory can illustrate a full image of the variations in the monitoring network.

Conclusion

The present study investigated the interaction effects of the stations using the copula-based simulation approach instead of the more typical method (i.e., multivariate regression analysis). In addition to investigating and confirming the correlations between the annual rainfall values of the stations using Kendall’s Tau, various Vine copulas including the C, D, and R Vines, and their Gaussian and dependent modes were compared. Ultimately, the R-Vine was selected as the best copula using the error investigation statistics. The results of investigating the internal R-Vine copulas showed that above 50% of the copulas were rotary, which made full coverage in all directions. In the end, the selected copula and its tree structure were used to investigate the interaction effects of the rain-gauge stations, and the rainfall values of the stations were estimated according to the values of other stations. The RMSE and NSE statistics were implemented to investigate the error rate and the efficiency of the Vine simulation approach. Moreover, the typical multivariate regression technique was implemented, and its results were compared with the results obtained for the vine simulation approach. The NSE statistic showed that the efficiency of all investigated stations was above 92%. In addition to the RMSE and NSE statistics, the results of the violin plot confirmed the certitude and performance of the Vine simulation approach. Comparing results of the multivariate regression and the Vine simulation technique confirmed the enhancement of the performance and reduction of the error rate of the latter in all stations. Thus, it was found that the Vine simulation approach had acceptable accuracy in estimating and simulating the rainfall values of each station according to the values recorded by the neighboring stations. The implemented approach provided values that were close to the real-world conditions as it used the copula functions and marginal distribution functions proportionate to the investigated series. Thus, the certitude of the model increases. In addition, the values of ITI and N(i) indicators were calculated for each station using the theory of entropy, and the results showed that the stations in the investigated area were sufficient. The investigated stations were on average, above-average, and surplus modes according to the ITI index, and this showed the area was conveniently monitored in terms of its rainfall. According to the N(i) index, Dashband station ranked as the best station in terms of communication with other stations and its convenient coverage of the plain. In other words, Dashband station was convenient in terms of offering rainfall variation data, and the information offered by it could be generalized to the whole area.