Abstract
The agricultural drainage engineering community is steadily shifting the design of subsurface drainage systems from the experience-based design approach to the simulation-based design approach. As with any design problem, two challenges are faced; firstly, how to determine all the input data required by the simulation model, and secondly to, a priori, anticipate what the performance of the designed system will be. This study sought to evaluate the performance of the WaSim model to simulate fluctuating water table depths (WTD), and drainage discharges (DD) in KwaZulu-Natal Province, South Africa. Saturated hydraulic conductivity (Ksat), which is an input to the WaSim model, was estimated by the Rosetta computer program, based on soil particle size distribution data, bulk density, and soil water retention characteristics at pressure heads of – 33 and – 1500 kPa. performance of the WaSim model was statistically assessed using the coefficient of determination (R2), coefficient of residual mass (CRM), mean absolute error (MAE), mean percent error (MPE), and the nash–sutcliffe efficiency (NSE). during the validation period, the WaSim model predicted WTDs with R2, CRM, MAE, MPE, and NSE of 0.86, 0.003, 4.9 cm, 6.0%, and 0.98, respectively. In the same validation period, the model predicted DDs with R2, CRM, MAE, MPE, and NSE of 0.57, 0.002, 0.30 mm day−1,11%, and 0.76, respectively. These results suggest that the use of Rosetta-estimated Ksat data as inputs to the WaSim model compromised its accuracy and applicability as a subsurface drainage design tool. Owing to the relatively low R2 value of 0.57, and that the WaSim model was empirically developed, we recommend further improvement on the calibration of the model for it to be suitable for application under the prevailing conditions. Also, in the absence of other means of determining Ksat, we caution the use of Rosetta-estimated Ksat data as inputs to the WaSim model for the design and analysis of subsurface drainage systems in KwaZulu-Natal Province, South Africa.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The provision of artificial agricultural subsurface drainage continues to be a key element in enhancing crop production potential of irrigated lands. The design of agricultural subsurface drainage systems has been a subject of discussion lately, and consequently, it has seen a number of improvements. According to ASAE (1999), the design of subsurface drainage systems is largely dependent on the experience in handling similar problems, also known as Experience-Based Design Approach (EBDA). This approach is, however, unreliable as it results in either an over- or under-designed subsurface drainage system. The development of drainage simulation models in the past five decades is steadily shifting the agricultural drainage engineering community from designing subsurface drainage systems based on the EBDA approach to a Simulation-Based Design Approach (SBDA) (ASAE 1999). One major advantage of the SBDA over the EBDA is the flexibility it provides to conduct analyses of the performance of subsurface drainage systems at various combinations of design parameters, as well as providing an idea of the system’s performance prior to installation. DRAINMOD model (Skaggs 1978), Water Simulation (WaSim) model (Hess et al. 2000), and SaltMOD model (Oosterbaan 2000) are some of the model examples which have been used as subsurface drainage design decision support tools in Australia (Yang 2008), India (Hirekhan et al. 2007), and Turkey (Bahceci et al. 2006). Unlike the EBDA, the application of these simulation models clearly shows that the SBDA is a simpler and cost-effective means of designing subsurface drainage systems.
Despite the promising progress and the steady growth in the development of drainage simulation models, Bastiaanssen et al. (2007) argue that the adoption of drainage simulation models, as agricultural water management decision support tools, still remains a challenge in most regions. Madramootoo et al. (2009), Salazar et al. (2008), Manyame et al. (2007), Bahceci et al. (2006), and Borin et al. (20000, attribute this scenario to (i) the unavailability of good quality soil hydraulic conductivity (Ksat) and Soil Water Retention Characteristics (SWRC) data, which are critical input parameters to many drainage simulation models, and (ii) the unavailability of user-friendly computer based drainage simulation models suitable for both the low and middle level agricultural water managers. A good example is the DRAINMOD model, which despite successful calibration and validation results in the sugarcane fields of KwaZulu-Natal, South Africa (Malota and Senzanje 2015), still faces adoption challenges. van der Merwe (2003) reports the lack of a drainage simulation model with an easy-to-follow graphical user interface and the unavailability of reliable Ksat and SWRC data as the two main determining factors to the adoption of a simulation based drainage design approach in the area.
Accurate field estimation of Ksat and SWRC require precise equipment, which is expensive and not readily available in most regions (Liu et al. 2017). On the other hand, laboratory estimation of these soil hydraulic parameters is time consuming and often over-estimate the parameters (Moriasi et al. 2007), thus rendering them unreliable for purposes of modeling soil hydraulic processes (Zhang et al. 2017). Researchers have however shown a keen interest in developing a number of indirect methods to estimate soil hydraulic parameters from easily measured and obtainable data (e.g., Rawls and Brakensiek 1985; Rawls et al. 1991; van Genuchten and Liej 1992; Pachepsky et al. 1996). Bouma and van Lanen (1987) regard such indirect methods as Pedotransfer Functions (PTFs), due to their ability to translate basic and easily accessible soil data and information to soil hydraulic parameters.
Rosetta (Schaap et al. 2001), with its neural network-based PTFs, is one of the successful computer programs that has been extensively used in soil hydraulic data scarce regions to estimate Ksat values and SWRCs (e.g., Salazar et al. 2008). Rosetta estimates these soil hydraulic parameters based on soil bulk density, soil particle size distribution (% sand, clay and silt), and one or two known points on the Soil Water Retention Characteristic Curve (SWRCC) (e.g., Zhang et al. 2017; Salazar et al. 2008; Wosten et al. 2001; Manyame et al. 2007). On the other hand, WaSim model (Hess et al. 2000), a subsurface drainage model with a graphical user interface and a relatively small data input requirement (Hirekhan et al. 2007), as opposed to the DRAINMOD model, offers an excellent opportunity to enhance drainage model adoption in regions such as KwaZulu-Natal, South Africa, where problems of poor agricultural drainage require urgent attention (van der Merwe 2003). The objective of this study was to assess the performance of the WaSim model to simulate the fluctuation of mid-drain spacing water table depth and drainage discharges using soil hydraulic input parameters estimated by the Rosetta computer program. The study was conducted in a sugarcane field in KwaZulu-Natal Province, South Africa.
Materials and methods
Description of the WaSim model
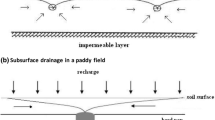
The WaSim model was developed by Cranfield University and HR Wallingford to simulate changes in soil water content and water table depths as a function of soil hydraulic properties, weather, and water management systems. The model, according to Hess et al. (2000), uses a three soil layer water balance existing between the upper (soil surface) and the lower boundaries (impermeable layer) as depicted in Fig. 1. Recharge to the soil system could either be in the form of rainfall, irrigation or seepage, with evaporation and deep percolation treated as outputs from each soil layer. In each case, deep percolation and capillary rise from one soil layer further constitute an input component into the underlying and overlying soil layers, respectively.
An overview of the multi soil layer water balance in the WaSim Model (after Hess et al. 2000)
The WaSim model adopts Eq. 1 (Youngs et al. 1989) to estimate drainage discharge on a daily basis.
where q is the daily drainage discharge (mm day−1), L is the drain spacing (m), Ksat is the overall saturated hydraulic conductivity (m day−1), soil water fraction
\(\varphi\) is the inside diameter of the drain pipe (m), h is the mid-drain spacing water table depth (m), and \(\beta\) is an exponent (dimensionless), which is dependent on drain spacing (L) and depth to the impermeable layer (\(d_{0}\)) (m), and is estimated as;
Otherwise,
Mid-drain spacing water table depths are estimated using Eq. 3, which requires volume water fractions at field capacity and saturation points to estimate the drainable porosity and the total daily net flux from the groundwater table.
where µ is the drainable porosity (dimensionless) and is given as:
where \(h_{i}\) is the water table depth (m) at any time (\(t = t_{1}\)), \(h_{2}\) is the water table depth at any time (\(t = t_{2}\)), \(V_{S}\) is the total daily net flux (capillary rise) from the groundwater table to the root-zone (mm day−1), \(\theta_{1} (h)\) and \(\theta_{2} (h)\) are soil water fractions (cm3 cm−3) as a function of soil depth (h) for water table positions at \(t_{1}\) and \(t_{2}\), respectively. The reader is referred to Hess et al. (2000), where a detailed theoretical description of the WaSim model is given.
Description of the rosetta
Rosetta (Schaap et al. 2001) is a computer program, which according to Salazar et al. (2008) implements five hierarchical PTFs to estimate soil SWRC, and saturated and unsaturated hydraulic conductivities. The program estimates the Ksat values based on surrogate data such as particle size distribution, bulk density and/or SWRC at one or two known points on the SWRCC (i.e., soil moisture content at – 33 and – 1500 kPa). The computer program estimates the soil parameters using the van Genuchten water retention model (Eq. 5) (Schaap et al. 2001)
where \(\theta\) is the soil water fraction (cm3 cm−3) at a given suction (h) (cm, taken positive for increasing suctions), \(\theta_{{\text{s}}}\) and \(\theta_{{\text{r}}}\) are saturated and residual soil water fractions (cm3 cm−3), respectively, n (> 1) is the measure of pore-size distribution, and α (> 0) is related to the inverse of air entry pressure (cm−1) (van Genuchten 1980).
Using Eq. 5, in connection with the Mualem (1976) pore-size distribution model (Eq. 6), yields the van Genuchten–Mualem model (Eq. 7), which according to van Genuchten (1980) and Schaap et al. (2001), is then used to estimate Ksat values.
where Se is the effective saturation (cm3 cm−3) (Vereecken et al. 2010; Jong van Lier and Pinheiro 2018) and is given as:
where \(K_{{\text{r}}}\) is the relative hydraulic conductivity, which is the ratio of hydraulic conductivity (K) at a certain soil water fraction (\(\theta\)) and suction (h) to the hydraulic conductivity at saturation (Ksat), i.e., \(K_{{\text{r}}} \left( {\theta ,h} \right) = \left[ {K\left( {\theta ,h} \right)} \right]/K_{{{\text{sat}}}}\),\(K_{0}\) is the matching point at saturation (m day−1) and is comparable, but not entirely equal to Ksat, and L (< 0) is an empirical connectivity parameter, in most cases taken as 0.5 (Mualem 1976).
Study site
The study was conducted in an irrigated sugarcane field in Pongola, KwaZulu-Natal Province, South Africa. The total area of the sugarcane field is 32 ha. Pongola is located on the north-eastern side of South Africa, close to the South African and Swaziland border in the KwaZulu-Natal province (27° 23ʹ 0ʺ South and 31° 37ʹ 0ʺ East). The area is dominated by clay-loam and clay soils (van der Merwe 2003) with fairly gentle slopes. The Aridity Index (AI) for the area is reported to be 0.12 (Malota and Senzanje 2015), which according to UNESCO (1979), is the ratio of mean annual rainfall (P) (mm) to mean annual reference potential evapotranspiration (ETo) (mm). This Aridity Index characterizes the area to be an arid region (0.03 < AI < 0.20). Thus, from April to October (winter season), crop production relies on irrigation only, while from November to March (summer season), some rainfall is available for crop production. The first subsurface drainage system was installed at the site in 1995 and was later replaced by a redesigned system in 2003 with a reduced drain spacing from 72 to 54 m, while the drain depth was maintained at 1.8 m.
Measurement of soil physical and hydraulic properties
Saturated soil hydraulic conductivity (Ksat) values were measured using an in situ method, i.e., the auger-hole method (van Beers 1983). Three 70 mm diameter auger-holes were drilled in each of the upper and middle sections, while four auger-holes were drilled in the lower section of the field. This made a total of 10 hand-drilled auger-holes in the whole 32 ha field, where in situ measurement of hydraulic conductivity were conducted. Determination of this number of testing locations was guided by Oosterbaan (1991), who recommends at least two sampling points per 10 ha. All the auger-holes were drilled to a depth of 1.7 m, well below the water table depth. The reader is referred to van Beers (1983) where a step by step auger-hole Ksat measurement procedure which was adopted in this study is presented. Prior to carrying out Ksat tests, five trenches were dug in the field (north, south, east, west and center) to a depth of 2.3 m from the soil surface. This was done to characterize any heterogeneities in soil layer boundaries and also to determine the number and thicknesses of the soil profile layers from the soil surface.
Saturated hydraulic conductivity values were also estimated using the Rosetta program, whose inputs were soil particle size distribution (% sand, silt and clay), soil bulk density (g cm−3), and soil moisture contents at – 33 kPa and – 1500 kPa. The soil profile from the soil surface to the drain depth level had two soil layers, with the upper soil layer being 0.45 m, while the second layer was 1.55 m thick. Soil particle size distribution were determined using undisturbed soil samples, which were collected using cores from the second soil layer at each of the 10 locations, where auger-hole tests were conducted. The soil samples were collected at random points within the same second soil layer in which the water table was resting during auger-hole Ksat measurement (between 0.50 and 1.60 m from the soil surface). First to be determined were the soil bulk densities, which were later followed by particle size analysis, using the standard thermo-gravimetric and sieve-pipette methods (Gee and Bauder 1986). These measurements were done under laboratory conditions in the School of Engineering, University of KwaZulu-Natal. The reader is referred to Warrick (2002), where detailed descriptions of the two standard methods adopted in this study are presented.
Determination of soil water retention values (h) (m) and their corresponding soil moisture contents (\(\theta\)) (cm3 cm−3) were done using a pressure plate in the hydraulic laboratory at the University of KwaZulu-Natal. Firstly, the soil samples were carefully submerged in water for 24 h in order to attain their saturated moisture content. This was later followed by placing the soil samples in the pressure chamber of the pressure plate and then subjecting them to pressures of 0 m, 20 m, 40 m, 60 m, 100 m, 120 m and160 m until no more water was observed to drain from the soil sample. This was followed by measuring the moisture content of the soil samples at each level of pressure head. The soil moisture content was measured using the thermo-gravimetric method which is again well described by Warrick (2002). The \(\theta (h)\) data for each of the 10 soil samples were fitted to the van Genuchten soil water retention model in the RETC computer program (van Genuchten and Leij (1992), from which SWRCC were developed. RETC (RETention Curves) is a computer program which is capable of describing hydraulic properties of unsaturated soils (van Genuchten and Leij (1992). The program adopts a nonlinear squares approach to estimate unknown model parameters based on observed retention and hydraulic conductivity data. The reader is referred to Daniel and Wood (1971) and van Genuchten and Leij (1992) for a thorough description of PTFs which are implemented by the RETC program.
Values of soil moisture content at – 33 and – 1500 kPa for each of the soil samples (obtained from the SWRCC), as well as their particle size distribution and bulk density data were imputed in the Rosetta computer program to estimate Ksat values. The Rosetta estimated Ksat values were compared to the in situ measured Ksat values using five statistical indices, namely the Mean Absolute Error (MAE) (El-Sadek 2007), the Pearson’s product-moment correlation (Coefficient of Determination) (R2) (Wang et al. 2006), also known as the Goodness-of-fit (Shahin et al. 1993; Legates and Mc Cabe 1999; Vazquez et al. 2002), the Coefficient of Residual Mass (CRM) (El-Sadek 2007), the Mean Percent Error (MPE) (Moriasi et al. 2007), and the Nash–Sutcliffe Model Efficiency (NSE) (Moriasi et al. 2007).
where Pi is the simulated value, Oi is the observed value, and N is the number of data entries.
MAE describes the accuracy of a model in making right predictions by measuring the average magnitude of errors between the simulated and the observed values (Legates and Mc Cabe 1999; Vazquez et al. 2002). According to Moriasi et al. (2007) and El-Sadek (2007), the MAE has a minimum value of 0.0, with values closer to 0.0 indicating a better agreement between measured and estimated values. The Goodness-of-fit measures how the estimated and measured data sets correlate and has minimum and maximum values of 0.0 and 1.0, respectively, with values closer to 1.0 indicating a better correlation between the two data sets (Shahin et al. 1993; Legates and Mc Cabe 1999; Vazquez et al. 2002). The CRM characterizes the tendency to over-estimate (CRM < 0) or under-estimate a property (CRM > 0) (El-Sadek 2007). The NSE measures the efficiency in predicting the values, with values closer to 1.0 indicating acceptable levels of efficiencies (Moriasi et al. 2007). On the other hand, MEP measures the magnitude of errors between the measured and predicted values relative to the measured values. MPE values closer to zero indicate that the predicted values are very close to the measured values (Legates and Mc Cabe 1999).
Measurement of water table depth and drainage discharges
Water table depths were measured at five piezometers which were manually augured at mid-drain spacing to a depth of 1.7 m from the soil surface. WTDs at each piezometer were measured by gradually lowering an electronic dip meter in the piezometer until a sound was heard. Under laboratory conditions, the measurement error of the electronic dip meter was determined to be ± 0.5 cm, which, according to van Beers (1983), is within the acceptable range. On the other hand, drainage discharges (mm day−1) were measured at drain out-let points which corresponded to mid-drain spacing where WTDs were measured. Measurement of DDs was done using a bucket and a timer.
Calibration and validation of the WaSim model
Weather data records in the form of daily potential evapotranspiration (PET), rainfall and minimum and maximum temperature were obtained from the Pongola SASRI weather station located about 3 km away from the study site. Considering that the data records had so many gaps, only the weather and drainage data set (water table depth and drainage discharge) from October 1998 to September 1999 were used for calibration purposes. On the other hand, weather and drainage data from September 2011 to February 2012 were used for model validation purposes. The calibration procedure adopted in this study was done on a trial and error basis (e.g., Dayyani et al. 2009). The maximum ponding depth on the soil surface was set at half the observed depth. Having noted that observed drainage discharges were nearly 10% less than the design drainage discharge, the leaching efficiency was set at 50%, as opposed to the default 60%. In addition to that, the soil system was set to allow seepage in-flow and out-flow to concurrently exist. The rest of the soil and crop parameters, and information presented in Table 1 (including the Rosetta-estimated Ksat value) were left un-altered during the calibration process. Time series of WTDs and DDs were simulated, using the WaSim model after every alteration of the calibration parameters. Simulated WTDs and DDs were compared to observed WTDs and DDs. Initially, the agreement between the two data sets was assessed by visual judgments from WTD and DD hydrographs (Moriasi et al. 2007; Dayyani et al. 2009), and later on, the R2, MAE, CRM, MPE, and NSE were applied.
Results and discussion
Performance of the rosetta to estimate K sat values
Figure 2 shows the correlation of Rosetta-estimated Ksat values and the in situ determined Ksat values. Despite the Rosetta having a tendency of slightly under-estimating Ksat values with a CRM of 0.031, the estimated and measured Ksat values correlated very well, with a very strong R2 value of 0.95 and a very small MAE value of 0.035 m day−1. Further to that, the Rosetta program estimated the Ksat values with a very high NSE of 0.98 and a low MPE of 3.2%. Comparatively, the Rosetta-estimated Ksat values were slightly better than those reported by Schaap et al. (2001), in which laboratory determined Ksat values were compared to Rosetta-estimated Ksat values. The good performance of Rosetta in this study was largely attributed to the comparison of in situ measured Ksat values to estimated Ksat values, as opposed to comparing laboratory determined Ksat values to the Rosetta-estimated values.
Soil water retention characteristic curves (SWRCCs)
Results of SWRCCs obtained by fitting measured \(\theta (h)\) data to the van Genuchten (1980) soil water retention model using the RETC program are shown in Fig. 3. In all circumstances, the RETC program fitted all the measured \(\theta (h)\) data very well to the van Genuchten soil water retention model, with very strong R2 values ranging from 0.975 to 0.992. As expected, in all situations, soil moisture content decreased with an increasing soil pressure head. In all the SWRCCs, the deflection toward equilibrium pressure head was between 20 and 60 m, which mirrored those of sandy-clay and clay-loamy soils reported by Carsel and Parrish (1988), and sandy soils reported by van den Berg et al. (1997). It was encouraging to note that the soil textural class of the top soil layer at the site was also clay-loam, as reported by van der Merwe (2003). Therefore, to some extent, the trend of SWRCCs in Fig. 3 corresponded well with their respective soil textural class at the site.
Soil water retention characteristic curves, fitted using the RETC program, based on the van Genuchten (1980) soil water retention model (black shaded circle Laboratory measured,solid line Fitted)
Performance of WaSim model during the calibration and validation periods
A summary of the statistical performance of WaSim model both during the calibration and validation periods is presented in Table 2. Relatively small MPEs of 12.8 and 11.0% were obtained during the calibration and validation periods in simulating DDs. These results indicate that the WaSim model simulated the DDs with minimal errors. However, during the same calibration period, the WaSim model registered an MPE of 36.3%, indicating that the model was not very accurate in simulating the WTDs. There was, however, an improvement in the accuracy of the WaSim model in simulating WTDs during validation period (MPE = 6%). Similarly, very small MAE values of 0.40 and 0.30 mm day−1 were obtained both during the calibration and validation periods in simulating DDs, implying that there were very small differences between individual pairs of simulated and observed DDs. Despite that, the results in Table 2 show that WaSim model registered a high MAE of 15 cm during WTD simulation in the calibration period, as compared to the MAE value of 4.9 cm registered during WTD simulation in the calibration period. The great improvement of the MAE results during WTD simulation in the validation period gives an indication that WaSim model can reliably simulate WTDs and DDs with a reasonable accuracy even with Ksat data inputs estimated by the Rosetta program. The inputting of the SWRC data as opposed to using only the soil particle size data as inputs to the Rosetta, during Ksat estimation might have improved the Ksat estimation performance of Rosetta, which in turn, further resulted in the reasonably good accuracy of the WaSim model to simulate WTDs and DDs during validation.
The CRM values obtained during WaSim model validation period showed that the model perfectly simulated both the WTDs and DDs (CRM \(\approx\) 0). On the other hand, WaSim model slightly under-estimated DDs during the calibration period (CRM > 0.0), while WTDs were slightly over-estimated (CRM < 1) during the same calibration period. The slight over-estimation of WTDs during the calibration period could be attributed to the allowing and inclusion of seepage flow from nearby naturally drained sugarcane fields during model calibration. On the other hand, the slight underestimation of DDs during the calibration period (CRM = 0.07) could be due to the slight underestimation of Ksat values by the Rosetta program, which consequently might have reduced groundwater flux to the drain pipes.
Simulated WTDs and DDs during calibration period correlated very well with their respective observed values, i.e., R2 = 0.95 for WTDs simulation and R2 = 0.97 for DDs simulation. During validation period, the model simulated WTDs and DDs with relatively moderate R2 values of 0.86 and 0.57, respectively, giving an indication that the WaSim model performance was better during the calibration period than the validation period in simulating both WTDs and DDs. Even though R2 values greater than 0.5 are acceptable in model simulation studies (Moriasi et al. 2007), the R2 value of 0.57 obtained during the validation period indicated the failure of the model to simulate DDs with a high level of confidence. Skaggs (1978) highlights that subsurface drainage discharge is one of the critical determinants of the performance of subsurface drainage systems, and, as such, needs to be determined accurately. In this regard, the ability of the WaSim model to simulate DDs needs to be improved further. On the other hand, the better model performance during the calibration as compared to the performance during validation period is a common phenomenon, since in this stage, model parameters are systematically adjusted to attain the best agreement between observed and simulated values. (e.g., Hassanpour et al. 2011; Dayyan et al. 2009).
Hydrographs of simulated and observed DDs and WTDs
Pairs of hydrographs for the simulated and observed WTDs and DDs closely followed similar patterns (Figs. 4, 5, 6 and 7). Even after rainfall and/or irrigation, simulated WTD and DD hydrographs followed the curving of the observed DD and WTD hydrographs reasonably well. Despite the use of Rosetta-estimated Ksat values to run the WaSim model in this study, it was encouraging to note that the model simulated deeper WTDs better (Fig. 4) than the DRAINMOD model, as reported by Malota and Senzanje (2015) in the same area of study. The disintegration of the soil profile into a multi soil layer water balance in the WaSim model (Fig. 1) entails treating the soil profile as a product of multiple soil layers. This approach might have described the soil profile much better as opposed to hydraulically treating the whole soil profile as a single homogenous entity.
A comparison of R2 values obtained in this study to those of Malota and Senzanje (2015), where DRAINMOD was tested to simulate the fluctuation of WTDs and DDs in the same area, indicates that DRAINMOD model predicted WTDs slightly better than the WaSim model during the validation period. In particular, the WaSim model failed to accurately simulate DDs. The possible explanation for this disparity could be the use of in situ Ksat values as soil hydraulic inputs in the DRAINMOD model, as opposed to the use of Rosetta-estimated Ksat values in WaSim model adopted in this study. Considering that most hydrological models are sensitive to Ksat values (Skaggs 1978), whenever possible, Dayyani et al. (2009) and Salazar et al. (2008) recommend the use of PTF-estimated Ksat values as inputs to hydrological models, only when in situ determined Ksat values are not available.
Concluding remarks and recommendations
This study evaluated the reliability of the WaSim model to simulate WTDs and DDs using Ksat values estimated by the Rosetta computer program. The general performance of the WaSim model during the validation period suggest that the model cannot reliably be used as a subsurface drainage design tool in the study area. The model failed to simulate DDs with a high level of confidence (R2 = 0.57). The results showed that the use of Rosetta-estimated Ksat data as inputs to the WaSim model compromised its performance and applicability, both as a subsurface drainage design tool, and for the development of artificial subsurface drainage design criteria. This study, therefore, recommends further improvement on the calibration of the WaSim model to accurately simulate both WTDs and DDs. Also, in the absence of other means of measuring Ksat, caution must taken when using the Rosetta-estimated Ksat data as inputs to the WaSim model for the design and analysis of artificial subsurface drainage systems in the KwaZulu-Natal Province, South Africa.
References
Agricultural land drainage: a wider application through caution and restraint. ILRI Annu Rep. International Institute for Land Reclamation and Improvement, Wageningen, The Netherlands.
Bahceci I, Dinc N, Tari AF, Argar AI, Sonmez B (2006) Water and salt balance studies, SaltMOD, to improve subsurface drainage design in the konya-cumra plain, Turkey. Agric Water Manag 85:261–271
Bastiaanssen WGM, Allen RG, Droogers P, Steduto P (2007) Twenty-five years modeling irrigated and drained soils: state of the art. Agric Water Manag 92:111–125
Borin M, Morari F, Bonaiti G, Paasch M, Skaggs RW (2000) Analysis of DRAINMOD performances with different detail of soil input data in veneto regions of Italy. Agric Water Manag 42(3):259–272
Bouma J van Lanen JAJ (1987) Transfer functions and threshold values: from soil characteristics to land qualities. In: KJ Beek (Eds) Quantities land evaluation, international institute of aerospace survey eaarth science ITC publication 6, pp 106–110
Carsel RF, Parrish RS (1988) Developing joint probability distributions of soil water retention characteristics. Water Resour Res 24:755–769
Daniel C, Wood FS (1971) Fitting equations to data. Wiley-Intersci, New York
Dayyani S, Madramootoo CA, Enright P, Simard G, Gullamundi A, Prasher SO, Madani A (2009) Field evaluation of DRAINMOD 5.1 under a cold climate: simulation of daily midspan water table depths and drain outflows. JAWRA 45(3):779–792
El-Sadek A (2007) Up-scaling field scale hydrology and water quality modeling to catchment scale. Water Resour Manage 21:149–169
Gee GW and Bauder JW (1986) Particle-size analysis. In: Klute, A (Eds) Methods of soil analysis, Part 1, Physical and mineralogical methods agronomy, 9, ASA, Madison Wisconsin, USA
Hassanpour B, Parsinejad M, Yazdani MR, Dalivand FS and Kossari H (2011) Evaluation of modified DRAINMOD in predicting groundwater Table fluctuations and yield of canola in paddy fields under snowy conditions (Case Study Rasht, Iran) Irrigation and Drainage, https://doi.org/10.1002/IRD.614
Hess TM, Leeds-Harrison P, Counsell C (2000) WaSim mxsanual. Inst Water Environ, Cranfield Univ, Silsoe
Hirekhan M, Gupta SK, Mishra KL (2007) Application of WaSim to assess performance of subsurface drainage system under semi-arid monsoon climate. Agric Water Manag 88:224–234
Jong van Lier Q, Pinheiro EAR (2018) An alert regrading a common misinterpretation of the van genuchten α parameter. Rev Bras Cienc Solo 42:e0170343
Klute A (1986) Methods of soil analysis part 1 physical and mineralogical methods monograph 9ASA and SSSA. Madison, WI
Legates DR, Mc Cabe GJ (1999) Evaluating the use of ‘goodness-of-fit’ measures in hydrological and hydro-climatic model validation. Water Resour Manage 35(1):47–63
Liu Z, Dugan B, Masiello CA, Gonnermann HM (2017) Biochar particle size, shape, and porosity act together to influence soil water properties. PLoS ONE. https://doi.org/10.1371/journal.pone.0179079
Madramootoo CA (1990) Assessing drainage on a heavy clay soil in quebec. Transact ASAE 33(4):1217–1223
Madramootoo C, Lee PS, Gopalakrishnan M (2009) International commission on irrigation and drainage (ICID): its objectives, achievements and plans. Irrig Drainage. https://doi.org/10.1002/ird.475
Malota M, Senzanje A (2015) Modelling Mid-span water table depth and drainage discharge dynamics using DRAINMOD 6.1 at a sugarcane field in pongola. South Africa Water SA J. https://doi.org/10.4314/wsa.v41i3.04
Manyame C, Morgan CL, Heilman JL, Fatondji D, Gerard B, Payne WA (2007) Modelling hydraulic properties of sandy soils of niger using pedotransfer functions. Geoderma 141:407–415
Moriasi DN, Arnold JG, van Liew MW, Bingner RL, Harmel RD, Veith TL (2007) Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans ASAE 50(3):885–900
Mualem Y (1976) A New model predicting the hydraulic conductivity of unsaturated porous media. Water Resour Res 12:513–522
Oosterbaan RJ (2000) SALTMOD: Description of principles and examples of application ILRI. Wageningen, The Netherlands
Oosterbaan RJ,Nijland HJ (1994) Determination of saturated hydraulic conductivity In: Ritzema HP (ds), Wageningen, The Netherlands, ISBN 90 70754 3 39
Pachepsky Y, Timlin DJ, Varallyay G (1996) Artificial neural networks to estimate soil water retention from easily measurable data. Soil Sci Soc Am J 60:727
Rawls WJ, Gish TJ, Brakensiek DL (1992) Estimating soil water retention from soil physical properties and characteristics. In: Stewart BA (ed) Soil Restoration Volume 17. Springer New York, New York, NY, pp 213–234. https://doi.org/10.1007/978-1-4612-3144-8_5
Rawls WJ, Brakensiek DL (1985) Prediction of soil water properties for hydrologic modeling. In: Jones EB, Ward TJ (eds) Proceedings SYMPOSIUM watershed management in the Eighties. April 30th – May 01st 1985, American Association of Civil Engineers, New York, Denver, CO, pp 293–299
Richards LA (1948) Porous plate apparatus for measuring moisture retention and transmission by soil. Soil Sci 66:105–110
Salazar O, Wesstrom I, Joel A (2008) Evaluation of DRAINMOD using saturated hydraulic conductivity estimated by a pedotransfer function model. Agric Water Manag 95(10):1135–1143
Schaap MG, Leij FJ, Van Genuchten MTH (2001) Rosetta: a computer program for estimating soil hydraulic parameters with hierarchical pedotransfer functions. J Hydrol 251:163–176
Shahin M, Van Oorschot HJL, De Lange SJ (1993) Statistical analysis in water resources engineering. Balk Publ, The Netherlands, A.A, p 394
Skaggs RW (1978) A water management model for shallow water table soils technical report No.134 Water Resources Research Institute. Univ North Carolina, Raleigh, NC, USA
Standards ASAE (1999) Standards engineering practices data, 46th edn. American soc agri eng. St. joseph. mich, USA
UNESCO (1979) Map of the world distribution of arid regions accompanied by explanatory notes UNESCO. France, Paris
van Beers WFJ (1983) The auger hole method: a field measurement of the hydraulic conductivity of soil below the water table ILRI. Wageningen, The Netherlands
van Genuchten MTH (1980) A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci Soc Am J 44:892–898
van Genuchten MTH, Leij FJ (1992) The RETC code for quantifying the hydraulic functions of unsaturated soils. environmental protection agency (EPA)/600/2–91/065. USEPA, Ada, Okla
van Den Berg M, KlamT E, van Reeuwijk LP, Sombroek WG (1997) Pedotransfer functions for the estimation of moisture characteristics of ferralsols and related soils. Geoderma 76:161–180
van Der Merwe JM (2003) Subsurface drainage design department of agriculture and environmental affairs. Pongola, KwaZulu-Natal
van Genuchten MTH, Leij FJ (1992) The RETC code for quantifying the hydraulic functions of unsaturated soils. Environmental Protection Agency (EPA)/600/2-91/1065, USEPA. Ada, Okla
Vazquez RF, Feyen L, Feyen J, Refsgaard JC (2002) Effect of grid-size on effective parameters and model performance of the MIKE SHE code applied to a medium sized catchment. Hydrol Processes 16(2):355–372
Vereecken H, Weynants M, Javaux M, Pachepsky Y, Schaap MG, van Genuchten MTh (2010) Using pedotransfer functions to estimate the van genuchten-mualem soil hydraulic properties: review. Vadoze Zone 9:795–820
Wang X, Mosley CT, Frenkenberger JR, Kladivko EJ (2006) Subsurface drain flow and crop yield predictions for different drain spacing using DRAINMOD. Agric Water Manage 79:113–136
Warrick AW (2002) Soil physics companion. CRC Press, New York, Washington, DC
Wosten JHM, Pachepsky YAA, Rawls WJ (2001) Pedotransfer functions: bridging the gap between available basic soil data and missing soil hydraulic characteristics. J Hydrol 2001(123–1):50
Yang X (2008) Evaluation and application of DRAINMOD in an australian sugarcane field. Agric Water Manag 95:439–446
Youngs EG, Leeds-Harrison PB, Chapman JM (1989) Modelling water-table movement in flat low-lying lands. Hydrol Process 3:301–315
Zhang Z, Glaser SD, Bales RC, Conklin M, Rice R, Marks DG (2017) The Design and evaluation of a basin-scale wireless sensor network for mountain hydrology. Water Resour Res. https://doi.org/10.1002/2016WR019619
Acknowledgements
This work was a continuation of a subsurface drainage simulation study that was conducted in the sugarcane fields of KwaZulu-Natal, South Africa in 2015 (Development of Technical and Financial Norms and Standards for Drainage of Irrigated Agriculture—Project K5/2026/14). We are very grateful to the South African Water Research Commission (WRC) for providing all the research funds. Special thanks must go to Dr. Aidan Senzanje and Mr Feston Chimphamba for the guidance they provided during data processing and manuscript preparation. We are also grateful to all staff members at Pongola Agricultural Office for all the support they rendered to us, especially during instrumentation and data collection. Our sincere thanks should also be extended to Dr. Khumbulani Dhavu for assisting with the in situ measurement of saturated soil hydraulic conductivity values.
Funding
This research was funded by the Water Research Commission, South Africa (Project K5/2026//14). The funders had no influence on the results, interpretation, and on the manuscript preparation. All authors have agreed to submit this manuscript to the journal of Applied Water Science.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
All authors have agreed to submit this manuscript to the journal of Applied Water Science.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Malota, M., Mchenga, J. & Chunga, B.A. WaSim model for subsurface drainage design using soil hydraulic parameters estimated by pedotransfer functions. Appl Water Sci 12, 171 (2022). https://doi.org/10.1007/s13201-022-01699-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-022-01699-z