Can sampling techniques improve the performance of decomposition-based hydrological prediction models? Exploration of some comparative experiments

Abstract

The development of sequence decomposition techniques in recent years has facilitated the wide use of decomposition-based prediction models in hydrological forecasting. However, decomposition-based prediction models usually use the overall decomposition (OD) sampling technique to extract samples. Some studies have shown that the OD sampling technique causes abnormally “high” performance of models owing to the utilization of future information, and this technique cannot be applied in practice. Several researchers have also proposed novel sampling techniques, such as semi-stepwise decomposition (SSD), fully stepwise decomposition (FSD), and single-model SSD (SMSSD). Moreover, an improved single-model FSD (SMFSD) sampling technique is proposed in this study. Four decomposition methods, namely discrete wavelet transform (DWT), empirical mode decomposition (EMD), complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN), and variational mode decomposition (VMD), are introduced in this study. A systematic investigation of the models developed using OD sampling techniques is conducted, and the applicability of SSD, FSD, SMSSD, and SMFSD sampling techniques is reasonably evaluated. The application of monthly runoff prediction using the five sampling techniques and four decomposition methods at five representative hydrological stations in Poyang Lake, China, shows that (1) EMD and CEEMDAN (including the improved EMD-based adaptive decomposition method) cannot be used to construct stepwise decomposition prediction models because the implementation of the stepwise decomposition strategy leads to a variable number of sub-series. (2) OD sampling techniques cannot develop convincing models for practical prediction because future information is introduced into the samples for model training. (3) Models developed based on SSD and SMSSD sampling techniques do not use future information in the training process, but suffer from severe overfitting and inferior prediction performance. (4) Models developed based on FSD and SMFSD sampling techniques can produce convincing prediction results, and the combination of the proposed SMFSD sampling technique and VMD develops prediction models with superior performance and significantly enhances the efficiency of the models.

Introduction

The study of hydrologic processes and the simulation and prediction of hydrologic time series are essential for the conservation and management of water resources (Ardabili et al. 2020). Therefore, advancing accurate models of the Earth’s various hydrologic phenomena and systems has been the focus of attention, and many predictive models have been studied in the past decades (Yaseen et al. 2015). These models are usually divided into physical and data-driven models (Kratzert et al. 2018; Zhang et al. 2015). Physical models have a long history of simulating, understanding, and predicting hydrologic processes as well as climate change (Ardabili et al. 2020; Todini 2007). However, the process of constructing physical models requires the input of large amounts of meteorological data, information on boundary conditions and physical properties, and high-power computing resources (Devia et al. 2015). Current physics-based models do not exhibit consistent performance across all scales and data sets, because they are only applicable to small watersheds (Grayson et al. 1992; Kirchner 2006). By contrast, data-driven models based on statistical modeling are popular because of their simplicity, low information requirements, and robustness (Chen et al. 2018; Huang et al. 2014; Shiri and Kisi 2010).

In particular, hydrologic prediction methods have been developed based on time-series models such as the autoregressive (AR), moving average (MA), autoregressive moving average (ARMA), and autoregressive integrated moving average (ARIMA) models (Bayer et al. 2017; Hien Than et al. 2021; Jones and Smart 2005; Valipour et al. 2013). However, hydrological processes are usually nonlinear and non-stationary, especially as human activities intensify leading to drastic and abrupt changes in hydrological time series. Traditional time-series models are no longer applicable to the forecasting of non-stationary, nonlinear, or variable streamflow patterns (Zuo et al. 2020b). Therefore, the refinement of the theory of machine learning (ML) and deep learning (DL) and the improvement of computer hardware performance have encouraged an increasing number of scholars to introduce ML and DL into hydrological prediction and enabled them to achieve remarkable results. These models include random forest (Desai and Ouarda 2021; Schoppa et al. 2020), extreme gradient boosting (Ni et al. 2020; Yu et al. 2020), support vector regression (SVR) (Gizaw and Gan 2016; Roushangar and Koosheh 2015), least squares support vector machine (Guo et al. 2021; Kisi 2015), adaptive neuro fuzzy inference system (Nourani and Komasi 2013; Roy et al. 2020), artificial neural networks (ANNs) (Rahman and Chakrabarty 2020; Araghinejad et al. 2011), and long short-term memory (LSTM) networks (Fang et al. 2021; Nourani and Behfar 2021). However, some hydrologists have emphasized that these data-driven models lack physical modeling and mathematical reasoning, and they are considered mere computational exercises (See et al. 2007).

Trends and periodic oscillations operating on multiple time scales have been extracted from hydrologic series by sequence decomposition techniques, which help reveal the driving forces of hydrologic series states (Nalley et al. 2012; Tosunoğlu and Kaplan 2018). The successful application of decomposition techniques in the analysis of trends and periodic behavior has inspired researchers to introduce them into data-driven models, which lead to the development of decomposition-based models. In decomposition-based models, hydrologic series are decomposed prior to the fitting process and predictions are obtained by aggregating the forecasts corresponding to each subseries. Several sequence decomposition techniques, such as discrete wavelet transform (DWT) (Adamowski and Sun 2010; Liu et al. 2014), empirical mode decomposition (EMD) (Huang et al. 2014; Meng et al. 2019), ensemble empirical mode decomposition (EEMD) (Li et al. 2018; Wang et al. 2018), complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN) (Fan et al. 2021; Rezaie-Balf et al. 2019), and variational mode decomposition (VMD) (Hu et al. 2021; Niu et al. 2020), have been documented to enhance the performance of hydrologic prediction models.

A majority of decomposition-based forecasting studies are devoted to improving the forecasting performance of models using improved decomposition methods and novel ML and DL techniques. However, most of these studies use overall decomposition (OD) sampling techniques to extract samples, and this approach shows sufficiently excellent fits, but no further studies extend to investigate their performance in practical forecasting. In fact, Napolitano et al. (2011) showed that EMD-based models developed using OD sampling techniques are hindcasting models rather than forecasting models due to that EMD decomposes the entire series and extracts samples from each sub-series, which means that the explanatory variables in all samples are actually calculated using future information unknown at the current time step. Zhang et al. (2015) further conducted hindcasting and forecasting experiments using EMD and DWT for ARMA and ANN, respectively. The results show that these models exhibit significantly inferior performance in the forecasting experiments compared with the hindcasting experiments, which ultimately concludes that the EMD- and DWT-based models are unsuitable for forecasting streamflow 1 month ahead at the study sites. The studies by Du et al. (2017), and Quilty and Adamowski (2018) on the applicability of OD sampling techniques also show that hybrid prediction models based on DWT and SSA may lead to erroneously “high” prediction performance and cannot be used to correctly handle realistic prediction problem.

Karthikeyan and Kumar (2013) developed a semi-stepwise decomposition (SSD) sampling technique and applied it to the ARMA model based on EMD and DWT. The results show that the DWT decomposition algorithm developed based on SSD can be used to model drought and other events with reasonable accuracy. Fang et al. (2019) also developed a fully stepwise decomposition (FSD) sampling technique to solve the problem of boundary distortion in the decomposition prediction process. Comparing the monthly runoff prediction performance of SVR models developed based on EMD and VMD, the results show that FSD sampling technique is a suitable alternative for developing convincing prediction models, and DWT and VMD can play a positive role in improving model performance. Zuo et al. (2020b) analyzed the defects of the decomposition prediction method and proposed a single-model semi-stepwise (SMSSD) sampling technique, and they experimentally demonstrated the effectiveness, efficiency, and accuracy of SMSSD–VMD–SVR in reducing boundary distortions, computational costs, and overfitting.

On the basis of previous research, we propose a single-model full stepwise decomposition sampling technique based on the ideas of FSD and SMSSD. By using monthly runoff data from representative stations of five rivers in the Poyang Lake Basin, we systematically evaluate the applicability of five sampling techniques (OD, SSD, FSD, SMSSD, and SMFSD) in data-driven prediction models using four different decomposition methods (DWT, EMD, CEEMDAN, and VMD) as preprocessing tools for streamflow series. This study aims to verify the suitability of OD sampling techniques for developing predictive models for practical use, to explore the applicability and limitations of several newly proposed sampling techniques. This study also compares the decomposition prediction models with the underlying prediction model, and it rationally analyzes the performance of the decomposition prediction model. The results of this study may provide effective advice and guidance for the practical application of decomposition prediction models.

Methodology

Review of decomposition-based methods

Changes in climate and intensified human activity have resulted in a high degree of nonlinearity and non-stationarity in observable hydrological data (e.g., runoff, rainfall, temperature, and water quality parameters) in most parts of the world. In the process of directly simulating and predicting highly nonlinear and non-stationary hydrological data, the noise part will seriously affect the training of the model and finally lead to the poor practical application effect of the model. However, the gradual improvement of the theory of signal decomposition methods has encouraged an increasing number of scholars to introduce signal decomposition methods to preprocess nonlinear and non-stationary data. This utilization has positive effects on hydrological predictive modeling owing to the ability of these methods to decompose nonlinear and non-stationary time series into collections of simpler components. These simpler components can be modeled more easily than the original series (Karthikeyan and Kumar 2013). The DWT and EMD are two preprocessing techniques that have been used earlier and widely. Among them, the decomposition outcomes of the DWT are sensitive to the selection of the mother wavelet and the decomposition level. Unfortunately, scientific support for the optimal determination of the two influential factors in hydrological applications is still lacking. In practice, many studies greedily test numerous combinations of mother wavelets and decomposition levels. The optimal combination is then chosen through evaluating the performance of the corresponding forecasting models, which is rather complicated and time-consuming. In essence, the DWT is analogous to filter banks, which recursively sift high-frequency components from residual series until a specified stopping criterion is satisfied and finally treat the residual series obtained in the last iteration as the trend term. Huang et al. (1998) proposed a novel adaptive signal decomposition method based on this idea, that is, EMD. This method can adaptively decompose the original signal into different intrinsic mode functions (IMF), but it has some problems, such as modal aliasing and boundary distortion. Wu and Huang (2009) developed a new method EEMD, which is a substantial improvement of the EMD. This method introduces Gaussian white noise to suppress modal aliasing to a certain extent, but the white noise amplitude and the number of iterations depend on human experience setting. The problem of mode aliasing cannot be overcome when the value is not properly set. Although increasing the number of ensemble averaging can reduce the reconstruction error, it also increases the computational cost, and the ensemble averaging of limited times cannot completely eliminate the white noise. Torres et al. (2011) proposed CEEMDAN to solve the problems of the EEMD. This method adds positive and negative paired auxiliary white noises to the original signal, which can cancel each other during ensemble averaging, thereby overcoming the problems of large reconstruction errors and poor decomposition completeness of the EEMD. At the same time, the calculation cost is greatly reduced. Recently, a novel multiple resolution decomposition technique, that is, VMD, has been proposed. Unlike the DWT, EMD, EEMD, and CEEMDAN, VMD addresses series decomposition problem in an optimization framework through concurrently searching for an ensemble of IMFs that can optimally reconstruct the original time series in a least-squares sense and are sparsely distributed in the frequency domain. More details of these decomposition techniques can be found in Mallat (1989), Huang et al. (1998), Wu and Huang (2009), Torres et al. (2011), and Dragomiretskiy and Zosso (2014).

Although the EEMD method can suppress modal aliasing to a certain extent, it also introduces other white noises into the original data, which is obviously unreasonable. On the basis of the above-mentioned analysis, four preprocessing techniques, namely, DWT, EMD, CEEMDAN, and VMD, are selected for comparative research to provide suggestions and guidance for better practical applications. In addition, the specific steps of the four decomposition methods can be referred to A.1, A.2, A.3, and A.4 in Appendix A.

Sampling technique

The length of the original time series $S$ is assumed to be $N$. The $m$ past observations lagging behind the data to be predicted are the candidate explanatory variables.

OD

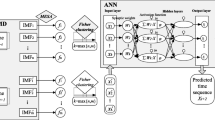
The OD sampling technique has been widely used in decomposition-based prediction research. Figure 1 shows the principle of the OD method. The specific explanation is as follows:

Fig. 1

The process of OD sampling technique

• (1) The original time series $\{ S_{1} ,S_{2} , \cdots ,S_{N} \}$ is decomposed into $K$ sub-series using decomposition method.

• (2) Each sub-series can construct $N - m$ samples, and these samples are divided into calibration and testing sets according to a certain proportion, and the model is trained using the calibration set samples of each sub-series (a total of $K$ models need to be trained).

• (3) The explanatory variables of the testing set of each sub-series are input into the corresponding trained model, and the prediction results for the response variables are obtained. The prediction results of the response variables of each sub-series are correspondingly summed and reconstructed to obtain the actual prediction results, and different evaluation indicators are used to evaluate and verify the model.

SSD

Future data are undeniably unknown at the forecasting stage. As a result, a stepwise decomposition strategy has to be adopted to predict future data over time in actual forecasting. However, in the OD sampling technique, the overall time series is decomposed only once before all of the samples are extracted, which is obviously based on the assumption that the future data are already known in each time step. Therefore, significant concern exists as to whether the explanatory variables of the samples obtained using the OD sampling technique contain additional information on the future data to be predicted, which is relative to their counterparts obtained using stepwise decomposition. An SSD sampling technique that is more suitable for practical applications is applied in the decomposition-based prediction research to address the forecasting risk that may arise from the unequal amount of information contained in the explanatory variables (Karthikeyan and Kumar 2013; Tan et al. 2018).

The SSD sampling technology is shown in Fig. 2, and the details are as follows:

Fig. 2

The process of SSD sampling technique

• (1) The original time series $\{ S_{1} ,S_{2} , \cdots ,S_{N} \}$ needs to be divided into calibration period $\{ S_{1} ,S_{2} , \cdots ,S_{P} \}$ and testing period $\{ S_{P + 1} ,S_{P + 2} , \cdots ,S_{N} \}$ to ensure that future information is not used in the modeling process.

• (2) $\{ S_{1} ,S_{2} , \cdots ,S_{P} \}$ is decomposed to extract the explanatory and response variables of all of the samples in the calibration period.

• (3) The data for the testing period are appended to the calibration series sequentially to acquire the samples in the testing period. Notably, after each extension of the series, the extended series is decomposed to extract the explanatory variables for only one sample from each sub-series. This appending-decomposing-sampling operation is repeated until all of data for the testing period have been successively appended to the calibration series.

• (4) Samples from the calibration set are used for model training, and a new model is built for each sub-series. The explanatory variables of the testing set are input into the corresponding models, and the prediction results for the response variables are obtained. The prediction results of the response variables of each sub-series are correspondingly summed and reconstructed to obtain the actual prediction results, and different evaluation indicators are used to evaluate and verify the model.

Compared with the OD sampling technique, the SSD sampling technique simulates the actual forecasting practice, and it adopts a stepwise decomposition method for the testing period series to generate samples. The explanatory variables of the last sample are input into the trained model to predict the result of the next timestamp.

FSD

An FSD sampling technique is applied in the decomposition-based hydrological forecasting study to maintain consistent performance of the prediction model throughout the calibration and testing periods, and it is fully followed by a stepwise decomposition strategy to extract all calibration and testing samples (Fang et al. 2019). The FSD sampling technique in Fig. 3 is explained as follows:

Fig. 3

The process of FSD sampling technique

The series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} \}$ is decomposed to obtain $K$ sub-series, and the last $m$ elements of each sub-series are extracted as potential explanatory variables of subsamples $\{ X_{{_{k,1} }}^{1} ,X_{{_{k,2} }}^{1} , \cdots X_{{_{k,m} }}^{1} \} ,\,\,\,\,k = [1,2, \cdots ,K]$. Thereafter, the data $S_{m + 1}$ are appended to $\{ S_{1} ,S_{2} , \cdots ,S_{m} \}$, and the extended series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} ,S_{m + 1} \}$ is decomposed. The last $m$ elements of each sub-series are extracted to constitute potential explanatory variables of subsamples $\{ X_{{_{k,2} }}^{2} ,X_{{_{k,3} }}^{2} , \cdots X_{{_{k,m + 1} }}^{2} \} ,\,\,\,\,k = [1,2, \cdots ,K]$. The series segment is gradually extended by appending the newly data one by one, and then, the corresponding samples are extracted. For the last sample, the series segment $\{ S_{1} ,S_{2} , \cdots ,S_{N - 1} \}$ is decomposed, and the potential explanatory variables of subsamples $\{ X_{{_{k,N - m} }}^{N - m} ,X_{{_{k,N - m + 1} }}^{N - m} , \cdots X_{{_{k,N - 1} }}^{N - m} \} ,\,\,\,\,k = [1,2, \cdots ,K]$ are extracted. The response variables of all samples are obtained by decomposing the overall time series $S$. All of the sample are split to make up the calibration and testing sets. Subsequent operations are the same as those for the OD and SSD decomposition techniques.

Although the results in Fang et al. (2019) show that the sampling technique works well, some logical problems still need to be solved. The response variables of all samples are obtained by decomposing the entire time series $S$, which is logically unreasonable, that is, the data in the testing period are unknown for the calibration period, and the data of the next time step are also unknown for the current time step. In practical application, it is impossible to decompose the entire time series $S$ to obtain the response variables of the calibration set samples. However, a more reasonable approach is to first divide the time series S into calibration period $\{ S_{1} ,S_{2} , \cdots ,S_{P - 1} ,S_{P} \}$ and testing period $\{ S_{P + 1} ,S_{P + 2} , \cdots ,S_{N} \}$. Starting from series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} \}$, new data are appended to series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} \}$ in turn, each series segment is decomposed into $K$ sub-series, and the last $m$ elements of each sub-series are extracted to constitute potential explanatory variables of subsamples. The response variables of the calibration set samples are obtained by decomposing the series segment $\{ S_{1} ,S_{2} , \cdots ,S_{P - 1} ,S_{P} \}$, because series segment $\{ S_{1} ,S_{2} , \cdots ,S_{P - 1} ,S_{P} \}$ is the data of the calibration period.

SMSSD

The largest difference between the SMSSD sampling technique and the SSD sampling technique is the selection of the response variables of the samples. The most intuitive impact of the SMSSD is to greatly reduce the number of models that need to be established. Furthermore, the SMSSD has been proven to have good performance and generalization in practical applications (Jing et al. 2022; Zuo et al. 2020a; Zuo et al. 2020b). The SMSSD sampling technique in Fig. 4 is specifically described as follows:

Fig. 4

The process of SMSSD sampling technique

• 1. The original time series $\{ S_{1} ,S_{2} , \cdots ,S_{N} \}$ is divided into calibration period $\{ S_{1} ,S_{2} , \cdots ,S_{P} \}$ and testing period $\{ S_{P + 1} ,S_{P + 2} , \cdots ,S_{N} \}$.

• 2. The calibration series $\{ S_{1} ,S_{2} , \cdots ,S_{P} \}$ is decomposed into $K$ sub-series. In the calibration set, the explanatory variable for the first sample is the top $m$ data of each sub-series $\{ X_{1,1} , \cdots ,X_{1,m} ,X_{2,1} , \cdots ,X_{2,m} , \cdots ,X_{K,1} , \cdots ,X_{K,m} \}$, and the response variable is $S_{m + 1}$. The subsequent extracted samples are successively added until the explanatory variables of the last sample are $\{ X_{1,P - m} , \cdots ,X_{1,P - 1} ,X_{2,P - m} , \cdots ,X_{2,P - 1} , \cdots ,X_{K,P - m} , \cdots ,X_{K,P - 1} \}$, and the response variable is $S_{P}$.

• 3. $\{ X_{1,P - m + 1} , \cdots ,X_{1,P} ,X_{2,P - m + 1} , \cdots ,X_{2,P} , \cdots ,X_{K,P - m + 1} , \cdots ,X_{K,P} \}$ is used as the explanatory variable for the first sample in the testing set. Data from the testing period are sequentially appended to the calibration series. Notably, each time a new data are appended, the appended series will be decomposed into $K$ sub-series, and the last $m$ data of each sub-series will be extracted in turn to construct the response variable of one sample, until $\{ S_{1} ,S_{2} , \cdots ,S_{N - 1} \}$ is decomposed and the explanatory variable is extracted. Finally, a total of $N - P$ samples of explanatory variables are obtained on the testing set.

• 4. The calibration set samples are used to train the model. Notably, only one model needs to be trained, and K models do not need to be trained separately for each sub-series because the response variable is the actual real data. The explanatory variables of the testing set are input into the trained model and predicted, and the model is evaluated using different evaluation indicators.

SMFSD

According to the idea of the FSD sampling technique, which is to maintain the consistency of the prediction model throughout the calibration and testing period, this study improves the SMSSD sampling technique and proposes the SMFSD sampling technique, which is shown in Fig. 5. The specific details are as follows:

Fig. 5

The process of SMFSD sampling technique

• 1. The original time series $\{ S_{1} ,S_{2} , \cdots ,S_{N} \}$ is divided into calibration period $\{ S_{1} ,S_{2} , \cdots ,S_{P} \}$ and testing period $\{ S_{P + 1} ,S_{P + 2} , \cdots ,S_{N} \}$.

• 2. The series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} \}$ is decomposed into $K$ sub-series, the explanatory variable of the first sample is $\{ X_{{_{1,1} }}^{1} , \cdots ,X_{{_{1,m} }}^{1} ,X_{{_{2,1} }}^{1} , \cdots ,X_{{_{2,m} }}^{1} , \cdots ,X_{{_{K,1} }}^{1} , \cdots ,X_{{_{K,m} }}^{1} \}$, and the response variable is $S_{m + 1}$. Then, the series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} ,S_{m + 1} \}$ is decomposed into K sub-series, the explanatory variable of the second sample is $\{ X_{{_{1,2} }}^{2} , \cdots ,X_{{_{1,m + 1} }}^{2} ,X_{{_{2,2} }}^{2} , \cdots ,X_{{_{2,m + 1} }}^{2} , \cdots ,X_{{_{K,m + 1} }}^{2} , \cdots ,X_{{_{K,m + 1} }}^{2} \}$, and the response variable is $S_{m + 2}$, and so on, until the series segment $\{ S_{1} ,S_{2} , \cdots ,S_{m} ,S_{m + 1} , \cdots S_{N - 1} \}$ is decomposed. Finally, $N - m$ samples can be obtained. The first $P - m$ samples are used as the calibration set, and the remaining samples are used as the testing set. Subsequent operations are the same as those for the SMSSD decomposition technique.

Underlying model LSTM

LSTM is widely used in hydrological forecasting research and has been proven to be one of the most effective methods in time-series forecasting (Cho and Kim 2022; Nourani and Behfar 2021; Xu et al. 2022). Traditional neural networks cannot connect previous information with the current time step when dealing with long-term dependencies. However, LSTM, as a special type of recurrent neural network, has a memory structure for learning long-term information (Hochreiter and Schmidhuber 1997). The LSTM network realizes temporal memory function through the switch of the gate and can solve the problem of gradient vanishing and explosion in recurrent neural network effectively. The key to LSTM is the introduction of a gating unit system that stores historical information through the internal memory unit—cell state unit, using different “gates” to let the network learn dynamically, that is, when to forget historical information or update cell state with new information. A further detailed description of the LSTM can be found in Appendix A.5. The LSTM is chosen as the underlying model for this investigation, and the determination of the LSTM parameters will be described in detail later in Section 3.3.6.

Model evaluation criteria

To evaluate the forecasting performance, three statistical indicators are used: the Nash–Sutcliffe efficiency coefficient (NSE), root-mean-square error (RMSE), and the percent bias (PBIAS). The NSE is a normalized statistic that determines the relative magnitude of the residual variance compared with the measured data variance, and the PBIAS measures the tendency of forecast values to be smaller or larger than that of the observed values (Moriasi et al. 2007). The definitions of these statistics are given as follows:

$$ NSE = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - P_{i} } \right)^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left( {O_{i} - \overline{O}} \right)^{2} } }}$$

(1)

$$ RMSE = \sqrt {\frac{1}{N}\sum\limits_{i = 1}^{N} {\left( {O_{i} - P_{i} } \right)^{2} } } $$

(2)

$$ PBIAS = \frac{{\sum\nolimits_{i = 1}^{N} {(O_{i} - P_{i} ) \times 100} }}{{\sum\nolimits_{i = 1}^{N} {O_{i} } }} $$

(3)

where $O_{i}$ is the measured value and $P_{i}$ is the simulated value.

Case study

Study area and data

Poyang Lake is located in the northern part of Jiangxi Province, China, on the southern bank of the Yangtze river. It is 173 km long from north to south and 16.9 km wide on average from east to west, with a total shoreline of about 1200 km, and is the largest freshwater lake in China. The main water supplies of the lake are precipitation, local rivers, and sometimes the Yangtze river (Han et al. 2018). The lake typically receives inflows from five major rivers (Ganjiang, Fuhe, Xiushui, Raohe, and Xinjiang) within the catchment, and it discharges to the Yangtze river via a narrow outlet at Hukou. Controlled by the subtropical monsoon, 55% of the annual rainfall occurs in March to June (Zhang et al., 2014), which leads to considerable seasonal water-level fluctuation (approximately 10 m). During the wet season (April to September), large floodplains become inundated and form a large lake covering an area > 3000 km². During the dry season (October to March of the next year), the inundation area of the lake shrinks to < 1000 km².

The data of this study are from Hydrology Bureau of Jiangxi Province, and representative hydrology stations of the five major rivers in the Poyang lake system are selected as research stations, namely Waizhou (WZ) station of Ganjiang, Lijiadu (LJD) station of Fuhe, Meigang (MG) station of Xinjiang, Dufengkeng (DFK) station of Raohe, and Wanjiabu (WJB) station of Xiushui. Figure 6 shows the location of Poyang Lake, five major rivers, and their representative station. Among them, the monthly streamflow data from 1956 to 2019 are used to verify and compare the techniques and methods used in this study, and Fig. 7 shows box plots of monthly runoff data for the five stations.

Fig. 6

Geographical overview of Poyang lake basin

Fig. 7

Box plots of monthly runoff data for five stations

Data normalization

In some ML models, especially DL, the optimization algorithm used to obtain the objective function will not work properly without data normalization due to the large fluctuation range of the original time series. In addition, data normalization can make the optimization algorithm converge faster and improve the prediction accuracy of the model. Therefore, all explanatory and response variables in this study are normalized to the range $[ - 1, \, 1]$. The normalization equation is given as follows:

$$ {\varvec{y}} = 2 \otimes \frac{{{\varvec{x}} - x_{\min } }}{{x_{\max } - x_{\min } }} - 1 $$

(4)

where ${\varvec{x}}$ and ${\varvec{y}}$ are the original and normalized values, respectively, while $x_{\max }$ and $x_{\min }$ are the maximum and minimum values of ${\varvec{x}}$, respectively. The multiplication and subtraction are element-wise operations. Notably, the parameters $x_{\max }$ and $x_{\min }$ are computed based on the calibration period data. These parameters are also used to normalize the testing period data to avoid using future information from the testing phases and enforce all samples to follow the calibration distribution.

Modeling process

Open-source library

This research is based on Python language and runs on Jupyter notebook. Pandas (https://github.com/pandas-dev/pandas) and Numpy (https://github.com/numpy/numpy) are used to manage and process time-series data. The implementation of DWT is based on the open-source library pywt (https://github.com/PyWavelets/pywt), the implementation of EMD and CEEMDAN is based on the open-source library PyEMD (https://github.com/laszukdawid/PyEMD), and the implementation of VMD is based on the open-source library vmdpy (https://github.com/vrcarva/vmdpy). TensorFlow (https://github.com/tensorflow/tensorflow) is used to build and train LSTM neural networks.

Data partitioning

In this study, the original monthly streamflow is divided into calibration and testing periods according to the ratio of 8:2. At the same time, 20% of the calibration set obtained by the sampling technique is used as the validation set for the determination of the hyperparameters of the model to reduce the overfitting of the model and enhance the generalization ability of the model. The strategy of augmenting the validation set is obviously a more conservative alternative to model calibration than simply evaluating the suitability of a model hyperparameter combination based on performance on the calibration set. These efforts help the predictive model maintain consistency in in-sample and out-of-sample performance.

Deficiencies of EMD and CEEMDAN

Fortunately, the parameters of EMD and CEEMDAN do not need to be manually adjusted, and the default values can be used directly. Moreover, EMD and CEEMDAN can adaptively determine the number of decomposed IMFs. However, we find a serious problem with EMD and CEEMDAN during the use of stepwise decomposition-based sampling techniques. Each time testing period data are appended to the calibration series; EMD and CEEMDAN require adaptive decomposition of new series segments. Unfortunately, the different lengths of the series segments may lead to different numbers of adaptive decompositions for EMD and CEEMDAN. Figure 8 shows the relationship between the number of IMFs decomposed and the series length decomposed using EMD and CEEMDAN. As the series length increases, the number of IMFs also shows an upward trend. Then, in the process of practical application, the number of IMFs decomposed adaptively by EMD and CEEMDAN may change as new observations are appended to the original time series. However, in the SSD sampling technique, only one sub-model is trained for each sub-series of samples. When new IMFs emerge, sub-models available to predict the new IMFs are insufficient. In addition, the number of IMFs decomposed each time for the FSD sampling technique may be different in the process of generating calibration samples by stepwise decomposition, which also hinders modeling of each sub-series separately. SMSSD and SMFSD sampling techniques do not need to model each sub-series, but the above-mentioned situation results in an inconsistent number of explanatory variables for each input model. In summary, EMD and EMD-based improved methods (e.g., EEMD and CEEMDAN) cannot be applied to predictive modeling that requires stepwise decomposition.

Fig. 8

Relationship between the number of IMFs and the length of the series decomposed using the a EMD and b CEEMDAN

Parameter selection and comparison of DWT

Mother wavelet and decomposition level are crucial for DWT, which also directly affects the performance of the final prediction model. Considerable literature has analyzed and discussed the optimal combination of DWT (Nourani et al. 2009; Seo et al. 2015; Seo et al. 2018; Shoaib et al. 2019; Shoaib et al. 2014; Shoaib et al. 2016). However, we find by synthesizing these studies that the decomposition level can usually adopt the empirical formula $L = {\text{int}} \;(\log [N])$, where $L$ represents the decomposition level, and $N$ represents the length of the time series to be decomposed. For discrete wavelet analysis, Daubechies wavelets have been commonly used mother wavelets, and Symmlets and Coiflets have been also applied in hydrologic wavelet-based studies (Adamowski and Sun 2010; Evrendilek 2014; Tiwari and Chatterjee 2010). Therefore, the performance of the applied model is investigated for different mother wavelets, including Haar wavelet (db1), Daubechies-2 (db2), Daubechies-4 (db4), Daubechies-6 (db6), Daubechies-8 (db8), Daubechies-10 (db10), Symmlet-2 (sym2), Symmlet-4 (sym4), Symmlet-8 (sym8), Symmlet-10 (sym10), Coiflet-6 (coif6), and Coiflet-12 (coif12).

Parameter selection and comparison of VMD

The four parameters that affect the performance of VMD decomposition are the decomposition level ($K$), the quadratic penalty parameter ($\alpha$), the noise tolerance ($\tau$), and the convergence tolerance ($\varepsilon$), respectively. As suggested by Zuo et al. (2020a), the values of $\alpha$, $\tau$, and $\varepsilon$ are set to 2000, 0, and $1 \times e^{ - 9}$, respectively. However, the performance of the VMD is very sensitive to the setting of $K$ (Xu et al. 2019). The time series cannot be fully decomposed when the value of $K$ is set too small, and modal aliasing will occur when the value of $K$ is set too large. We found through experiments that the optimal $K$ value can be determined by checking whether center frequency aliasing occurs in the last IMF. Taking VMD of WZ for example, we evaluated $K$ from $K = 2$ to $K = 12$. Figure 9a shows the results and spectrograms of IMF6 to IMF8 when $K = 8$. As observed, IMF8 exhibits obvious modal aliasing phenomenon. The value of $K$ for the VMD decomposition of WZ is chosen to be 7 to satisfy the orthogonality constraint and avoid spurious components as much as possible. Figure 9b shows the decomposition results and spectrograms of IMF5 to IMF7 when $K = 7$. It can be seen that there is no modal aliasing phenomenon, indicating that the selection of $K$ value of 7 is reasonable. The four other stations use the same method to determine the $K$ value.

Fig. 9

Decomposition results and spectrum of WZ station when a K = 8, b K = 7

Hyperparameter selection of LSTM model

There are many hyperparameters of the LSTM model, among which the hyperparameters that greatly impact on the performance of the model include the number of LSTM layers, the number of LSTM layer units, batch size, dropout rate and learning rate. Determining the optimal combination of these hyperparameters remains difficult, and random search and optimization algorithms can be used to optimize these hyperparameters. However, these methods are very time-consuming. In practical applications, the hyperparameters of the model are usually adjusted manually for practical problems, and a relatively optimal model is trained within a limited time. Therefore, an experimental method that increases or decreases the values of these hyperparameters is used to determine the optimal hyperparameter values for the LSTM modeling. The amount of data in this study is only 756, and the sub-series after VMD decomposition is stable. Thus, a single-layer LSTM model is selected to fit the training samples considering the performance and efficiency of the model. The batch size determines the number of samples used in each training model, to solve the problem of large data samples being fed into the model and causing the computer system to crash simultaneously. Since the total number of samples in this study is small, the batch size is set to the same value as the number of calibration samples, that is, all training samples participate in the training of the model at the same time. After the number of layers and batch size of the LSTM are determined, the learning rate is adjusted first. Then, the number of LSTM layer cells and dropout rate are adjusted. The other hyperparameters of the LSTM model are set to the default values used by TensorFlow.

The IMF1 of the WZ station is used as an example of hyperparameter tuning to demonstrate the experimental procedure. First, the 8-1 LSTM network structure (8 LSTM units, 1 output unit) is initialized. Furthermore, a dropout layer is added after the LSTM layer to prevent the model from overfitting, and the dropout rate is initially set to 0. Given that the monthly runoff is predicted, $m$ is chosen to be 12, and $m$ represents the past $m$ observations as the explanatory variable. The stopping condition is reached when the LSTM model converges. The training will be performed 10 times for a specific hyperparameter combination to reduce the impact of random initialization of weights on the model, and the model with the lowest average RMSE in the 10 times during the validation period is selected as the optimal model.

In this study, we investigate 12 learning rates (Fig. 10) for training the LSTM models. It can be clearly seen from Fig. 10 that a small learning rate can cause the model to converge very slowly (e.g., the learning rates are 0.0001, 0.0003, 0.0007, and 0.001), and a large learning rate can lead to severe oscillations in the process of model convergence (e.g., the learning rate is 0.7). Among them, the learning rates of 0.03, 0.07, and 0.1 can converge quickly and have less fluctuation. Comparing the learning rates of 0.03, 0.07, and 0.1 shows that the loss curve corresponding to the learning rate of 0.03 is smoother and more stable. Therefore, a learning rate of 0.03 is chosen as the optimal learning rate for IMF1 in the WZ station. After the optimal learning rate is determined, we design 8 levels from 8 to 64 with an interval of 8 as the number of LSTM layer units, and 10 levels from 0 to 0.9 are designed with an interval of 0.1 as the dropout rate. A total of 80 models are built to screen the best combination of LSTM layer unit number and dropout rate, and the results are shown in Fig. 11. According to Fig. 11, we can know that the model has the lowest RMssSE of 0.0095 on the validation set when the number of LSTM layer units is 32 and the dropout rate is 0. From the above-mentioned research, it is finally determined that the optimal prediction structure of IMF1 at WZ station is a single-layer LSTM network of 32-1, and the learning and dropout rates are 0.03 and 0, respectively. The hyperparameter selection of all subsequent models refers to the hyperparameter adjustment procedure of the above-mentioned WZ station IMF1. Notably, the final predicted streamflow of the OD, SSD, and FSD sampling techniques is obtained by summing the predictions for the sub-series, and the SMSSD and SMFSD sampling techniques are able to obtain the predictions directly.

Fig. 10

Loss lines with different learning rates for the IMF1 of VMD for WZ station

Fig. 11

RMSE for different combinations of units and dropout rate of LSTM

Result analysis

Figures 12, 13, and 14 show the criteria RMSE, NSE, and PBIAS for prediction using five sampling techniques (OD, SSD, FSD, SMSSD, and SMFSD) based on the LSTM model at five stations (WZ, LJD, MG, DFK, and WJB). Among them, the horizontal coordinate represents the calibration, validation, and testing periods of different sampling techniques. The first coordinate in the vertical coordinate represents the VMD, and the remaining coordinates represent the different wavelets of the DWT, as mentioned in Section 3.3.4.

Fig. 12

NSE of LSTM based on different sampling techniques and decomposition methods on calibration set, validation set, and testing set at a WZ, b LJD, c MG, d DFK, and e WJB

Fig. 13

RMSE of LSTM based on different sampling techniques and decomposition methods on calibration set, validation set, and testing set at a WZ, b LJD, c MG, d DFK, and e WJB

Fig. 14

PBIAS of LSTM based on different sampling techniques and decomposition methods on calibration set, validation set, and testing set at a WZ, b LJD, c MG, d DFK, and e WJB

Applicability of the OD sampling technique

Model performance gap between OD- and SSD-based sampling techniques

As shown in Figs. 12, 13, and 14, the SSD-based model has the best performance. Specifically, it has lower RMSE, higher NSE, and PBIAS closer to 0 regardless in the calibration, validation, or testing period. In addition, the model does not have overfitting, which is our most ideal and expected result. This result seems to indicate that the decomposition-based prediction model developed using the OD sampling technique can be well applied in practice. However, when we attempted to put this method into practice, we find that this deduction is not possible. The OD sampling technique decomposes the entire time series once before extracting all samples and dividing the calibration and test sets. The premise of this strategy is that future data are known at each time step. In prediction practice, we cannot obtain information about future data at the current moment, which is also the fundamental reason why OD sampling technology cannot be applied in practice. Therefore, the problem we need to solve is the way to use the currently known information to better predict the future when the future information is unknown. Based on this point of view, follow-up research needs to strictly ensure that additional information related to future data is not introduced into the explanatory variables, which will help us make a reasonable assessment of the applicability of the OD sampling technique.

Further analysis of the evaluation criteria of the SSD-based model according to Figs. 12, 13, and 14 shows that the SSD-based model suffers from severe overfitting. The model shows excellent results during the calibration and validation periods, but it is not as satisfactory during the testing period. Comparing the principles of OD and SSD sampling techniques reveals that the difference between the two techniques is that SSD is divided into calibration and testing periods, and the data from the calibration period are decomposed to extract calibration and validation samples, while the testing samples are extracted by a stepwise additional decomposition method, which is consistent with the practice predictions. The new observations we obtain at the current moment are appended to the historical data, and the decomposition process is re-executed to obtain the explanatory variables for the input model. Therefore, the above-mentioned comparison of the rationale and predictive performance of the two sampling techniques shows that the OD sampling technique introduces additional information in the explanatory variables of the sample. By contrast, the actual forecasting work produces explanatory variables that only contain information from past data records. Once the explanatory variables contain information to be forecasted in the future, the fitting process becomes the hindcasting process. Therefore, the favorable values of the evaluation criteria during the testing period shown in Figs. 12, 13, and 14 indicate that the DWT–LSTM and VMD–LSTM models developed using the OD sampling technique have superior hindcasting performance. On the other hand, combined with the improved results of the OD sampling technique over the SSD sampling technique, the undesirable evaluation criteria in the testing set also reveal their inferior forecasting performance.

In addition, Table 1 also gives the predictive metric criteria for the models based on the two decomposition methods of OD, i.e., EMD and CEEMDAN, and it can be seen that each decomposition method exhibits a favorable hindcasting performance. Unfortunately, as mentioned in Section 3.3.3, the decomposition levels of EMD and CEEMDAN cannot be actively controlled, and one of the most immediate problems this leads to is that the levels of decomposition may be different each time during the stepwise-appended decomposition. Therefore, with the current problems of EMD and CEEMDAN methods, they cannot be applied to the prediction process based on stepwise decomposition.

Table 1 Performance criteria for EMD- and CEEMDAN-based models developed using OD sampling technique

Fundamental explanation for the performance gap between OD and SSD

The previous section has pointed out the fallibility of OD sampling techniques in developing convincing predictive models. However, the primary cause of this result is that boundary distortion introduces errors into the construction of decomposition-based models. These errors arise from the extrapolation of the boundary decomposition components. In fact, this extrapolation is performed owing to the unavailability of future data points as decomposition parameters. For this purpose, we further explored the effect of boundary distortion on the decomposition errors. The first 600 monthly streamflow data from WZ station, i.e., $S_{1 - 600} = [q_{1} ,q_{2} , \cdots q_{600} ]$, and a one-step additional series of $S_{1 - 600}$, i.e., $S_{1 - 601} = [q_{1} ,q_{2} , \cdots q_{600} ,q_{601} ]$, are chosen, with the assumption that the VMD method is applied to the decomposition of $S_{1 - 600}$ and $S_{1 - 601}$. Theoretically, the $IMF_{1}$ for the VMD of $S_{1 - 600}$ should be maintained by the $IMF_{1} (1:600)$ for the VMD of $S_{1 - 601}$, given that $S_{1 - 600}$ is maintained by $S_{1 - 601} (1:600)$, where $(1:600)$ denotes the data from 1 to 600 intervals of 1. However, the decomposition results for $S_{1 - 600}$ and $S_{1 - 601}$ exhibit completely differently on the boundaries (see Fig. 15a, b) and show a high consistency beyond the occurrence of boundary distortion on the right side, thereby demonstrating that VMD is sensitive to the addition of new data. Furthermore, the same conclusions as for VMD are obtained for DWT, EMD, and CEEMDAN. The boundary distortion in the SSD sampling technique introduces a small decomposition error for the calibration set, but a large error for the testing set. The reason is that the calibration period is concurrently decomposed, whereas the validation set is sequentially appended to the calibration set and decomposed. We can generally ignore the decomposition error in the calibration period, but the error in the testing period is difficult to ignore. The difference between the blue and red lines shown in Fig. 15c is directly responsible for the paucity of generalization of the SSD sampling technique.

Fig. 15

Examples of the boundary effects for the VMD method on monthly runoff data at the WZ station: a, b sensitivity to appending one data point, c differences between sequential and concurrent testing decompositions, and d differences between the summation of the sequential and concurrent testing decompositions

Applicability of the FSD sampling technique

The above-mentioned research demonstrates that OD and SSD sampling techniques cannot be used to develop convincing predictive models. This subsection concentrates on the applicability of the FSD sampling technique.

The results show that the performance of SSD sampling technique is unsatisfactory, but its stepwise decomposition strategy is meaningful for practical applications. Compared with SSD, the FSD sampling technique guarantees that all samples are extracted according to the stepwise decomposition strategy. All samples have the same distribution on the calibration, validation and testing sets, which can effectively reduce the potential overfitting problem of the model and improve the generalization ability of the model. As shown in Figs. 12, 13, and 14, the performance of the model developed based on FSD is weaker than that of the model developed based on SSD on the calibration and validation sets. However, DWT−LSTM or VMD−LSTM shows a marked improvement on the testing set. The performance of the model has been significantly improved. For the WZ station, the RMSE of FSD-based DWT−LSTM is 6.61% to 35.86% lower than that of SSD-based DWT−LSTM on the testing set. In particular, no negative values of NSE are observed and the values are greater than 0.39 in the DWT−LSTM model developed based on FSD. Similarly, the RMSE and NSE of the FSD-based VMD−LSTM are 3.94% lower and 8.14% higher than those of the SSD-based VMD−LSTM in the testing set. Similar conclusions to the above can be obtained at other stations. The results show that FSD reduces the potential overfitting of the model under the premise that it can be used in practice, and the two-stage training of calibration and validation ensures the generalization of the model. The choice of different mother wavelets greatly impacts the performance of DWT−LSTM, and choosing a suitable mother wavelet is crucial when the time series exhibits different non-stationarity (e.g., different stations). Compared with DWT, VMD shows superior stability (highest NSE and relatively low RMSE), which will help improve practical applications.

Applicability of the SMSSD sampling technique

As mentioned in Section 4.1.2, the boundary distortion in the SSD sampling technique introduces a small decomposition error for the calibration and validation sets and a large decomposition error for the testing set. Therefore, the error caused by the boundary distortion can seriously affect the prediction results for each sub-series during its modeling. The SMSSD sampling technique is based on three key remarks: (1) the decomposition affected by the boundary may contain some valuable information for building the actual prediction model, (2) the distribution of the testing samples can be different from that of the calibration samples, and (3) the decomposition error on the testing set can be eliminated by summing the signal components into the original signal. As shown in Fig. 15d, the sum of the sequential testing decompositions is close to the original time series. However, the sum of the sequential testing decompositions cannot completely reconstruct the testing set. This inadequacy is mainly caused by setting the VMD noise tolerance ($\tau$) to 0 in this work (Section 3.3.5) rather than the introduced testing decomposition errors.

As shown in Figs. 12, 13, and 14, the improvement of SMSSD for the model effect on the testing set is insignificant and is much less than the performance of the FSD-based sampling technique. Figure 16a gives the violin plots for the NSE of the SSD-based and SMSSD-based LSTM models, and the effect of SMSSD is insignificantly improved compared with that of SSD. Moreover, for the VMD−LSTM model, SMSSD exhibits inferior performance to SSD at all five stations. According to what is mentioned in the literature (Zuo et al., 2020b), the validation set is from a part of the testing set. However, as mentioned in Section 3.3.2, the validation set in the present study is selected from the last 20% of the calibration set. For this reason, we try the SMSSD sampling technique with the validation set coming from the testing set (SMSSD2), and the results are shown in Tables 2, 3, and 4, and Fig. 16b shows the violin plots of the NSE for the LSTM models based on SMSSD and SMSSD2. Ultimately, we find that SMSSD and SMSSD2 are not fully effective in improving the prediction performance. This finding indicates that SMSSD (SSD and SMSSD2) sampling techniques may not achieve satisfactory results in practical prediction.

Fig. 16

a SSD-based and SMSSD-based and b SMSSD-based and SMSSD2-based violin plots of the DWT-LSTM model NSE

Table 2 NSE of the model developed using SMSSD2 sampling technology

Table 3 RMSE of the model developed using SMSSD2 sampling technology

Table 4 PBIAS of the model developed using SMSSD2 sampling technology

Applicability of the SMFSD sampling technique

The previous subsection shows that SMSSD (SMSSD2) exhibits less than satisfactory results, but the idea of building a single model for all sub-series is worthwhile. Compared with SSD, FSD significantly improves the prediction of the model. Therefore, we further propose the SMFSD sampling technique on the basis of the ideas of FSD and SMSSD and test its performance. The results are shown in Figs. 12, 13, and 14. Among them, SMFSD shows the best results at WZ station, especially the NSE of VMD−LSTM model exceeds 0.6 in the testing set. The NSE and RMSE of SMFSD at other stations are slightly better than FSD. The VMD−LSTM model based on SMFSD has better performance than the DWT−LSTM model based on SMFSD. This finding indicates that it is feasible to build a single model for all sub-series. Compared with FSD, SMFSD not only improves the prediction performance of the model but also reduces the number of models that need to be manually tuned and is K times faster than FSD in terms of training speed (K denotes the number of decomposed sub-series). In practical applications, SMFSD-based sampling techniques can improve the training efficiency of the overall model while satisfying better performance.

Discussion

Extent to which decomposition-based strategies improve model performance

The essence of decomposition-based strategy forecasting is to convert a non-stationary time series into multiple stationary sub-series with different frequencies using different preprocessing methods (e.g., DWT, EMD, and VMD), and the model usually has better forecasting performance for the stationary series. As the idea of OD, SSD, and FSD, the prediction of each smooth sub-series is performed and reconstructed to obtain the final prediction results. However, the intractable boundary distortion is the major limitation of such methods. SMSSD and SMFSD also utilize preprocessing methods, but the essence of these methods is to extract more features from the time series as inputs to the model for improving the prediction accuracy. In summary, the prediction performance of the model is closely related to the volatility and smoothness of the original time series. For this reason, we further explore the performance gap between direct prediction and decomposition prediction based on sampling techniques. Table 5 shows the evaluation criteria for the direct use of LSTM for prediction. According to Table 5, we can see that the prediction results obtained by using the LSTM model directly do not differ much from the performance of the models developed using FSD and SMFSD. Taking the SMFSD−VMD−LSTM with the best overall performance as an example, the SMFSD−VMD−LSTM has the highest NSE improvement of 16.67% and the lowest improvement of 1.82% at the five stations compared with the direct LSTM prediction. The performance of decomposition-based prediction models does not always perform well, and the differences in performance are also attributable to errors caused by manual tuning. These results demonstrate that the decomposition-based prediction methods do not appear to significantly improve model performance. With the inability of the signal decomposition method to address the boundary distortion problem, the decomposition-based prediction method does not provide a significant improvement over the direct prediction method. Of course, this conclusion may only be applicable to the study area of this work at the moment, and we can try to study different hydrological data from different areas for further verifying this conclusion.

Table 5 Performance criteria for direct prediction using LSTM model

Effect of sample consistency on the model

Section 4.1 emphasizes that the OD sampling technique is unsuitable for the development of predictive models. The reason is that the future information that needs to be predicted is introduced into the explanatory variables of the sample, which leads to exceptionally “high” accuracy. The SSD sampling technique is proposed and widely applied to overcome the shortcomings of OD. However, the experimental results in this study show that the SSD-based model suffers from serious overfitting problems due to the fact that the samples of the calibration and validation sets come from a concurrent decomposition of the calibration series, while the samples of the testing set come from a stepwise decomposition of the testing series, and these two decompositions lead to samples with different distributions in the calibration and testing sets. The model may have high precision on the calibration and validation samples, but shows unsatisfactory performance on the test samples with different distributions. However, the underlying cause of this phenomenon is due to the boundary distortion. If no boundary distortion occurs, then the sub-series obtained by concurrent decomposition and stepwise decomposition should be the same, and the results in Fig. 14c show that the sub-series are different. When we use the calibration samples with basically no boundary distortion to train and predict the test samples with boundary distortion, it will naturally lead to reduced model prediction performance and overfitting. FSD uses stepwise decomposition to obtain all samples, and it ensures that all samples have the same distribution. The unknown information introduced by the boundary distortion is used as part of the model training, which improves the prediction accuracy of the model while ensuring that the model without overfitting. Meanwhile, SMSSD encounters the same problem as SSD, that is, sample inconsistency, which also prevents the model performance from being improved. In Section 4.2, we attempt to keep the same distribution of the validation and testing set samples, but this attempt is ineffective. SMFSD ensures that each sample has the same distribution as FSD. Thus, the effect of SMFSD is significant and no overfitting problem is observed. Therefore, it is crucial to ensure the consistency of the samples at each stage in the actual prediction, and it is necessary to consider whether each sample has the same distribution when a significant performance gap or overfitting is detected between the calibration and test sets.

Additional features to improve the performance of the model

The results in Section 5.1 show that the models developed by the FSD and SMFSD sampling techniques exhibit better performance than the single LSTM model. However, the performance of the model needs to be further improved, with more research focusing on accurate modeling of the decomposed random components and improvements to the decomposition algorithm. From the signal processing point of view, boundary distortions are difficult to eliminate because the future information is unknown to us. Therefore, when we try to use a decomposition-based prediction model, the unknown information introduced by the boundary distortion should be part of the model training. Moreover, most of the studies decompose the prediction for the historical data of a certain time series. Thus, we should attempt to introduce more relevant features for analysis and filter features for the actual significance of the target that needs to be predicted. For time series with certain periodicity, using time as a feature will likely improve the performance of the model. As in the case of the monthly streamflow data in this study, monthly streamflow usually has a strong correlation with monthly precipitation, which can be observed as a period of 12 months. Therefore, we try to use month as a feature, and the prediction results of VMD-LSTM models developed based on four sampling techniques (i.e., SSD, FSD, SMSSD, and SMFSD) at the WZ station are shown in Fig. 17. It can be seen that introducing month as a feature can indeed improve the prediction performance of the models, and a significant improvement in NSE and a significant reduction in RMSE are observed for each model. This result indicates that the introduction of more effective features can further improve the prediction performance of the models.

Fig. 17

a NSE and b RMSE of VMD-LSTM model developed based on four sampling techniques at WZ station

Conclusions

In traditional decomposition-based forecasting studies, OD sampling techniques are more commonly used. However, some recent studies have shown that OD sampling techniques cannot develop convincing forecasting models, and the decomposition of the whole time series introduces future information and thus leads to anomalously high accuracy. To address this problem, many scholars have also proposed improvements to the OD sampling technique, namely SSD, FSD, and SMSSD. These improvements can effectively solve the problem of using future information and improve the accuracy of the models. An improved sampling technique, that is, SMFSD, is also proposed in our work in conjunction with previous studies. These studies indicate that the proposed sampling technique can improve the prediction accuracy well while solving the problem of using future information, but effective comparison is still lacking. For this purpose, we select the LSTM model, which has been verified to have excellent prediction effect in recent years, as the base model. We also use the monthly runoff data from five representative hydrological stations of five rivers in Poyang Lake basin as the research samples to conduct a systematic comparison for the five sampling techniques mentioned above and combine four decomposition methods, namely DWT, EMD, CEEMDAN, and VMD. The reasons why OD sampling techniques cannot be applied in practice are explored, and the applicability of SSD, FSD, SMSSD and SMFSD is analyzed in the hope of bringing effective references and guidance for practical applications. The main conclusions are as follows:

• 1. EMD and CEEMDAN are adaptive decompositions. The number of sub-series obtained from each decomposition cannot be the same when the stepwise additional decomposition strategy is used. Therefore, EMD and CEEMDAN (including the improved adaptive decomposition methods based on EMD) cannot be used to construct a stepwise decomposition prediction model.

• 2. The comparison of prediction results based on OD and SSD sampling techniques verifies that the OD sampling technique indeed introduces future information components, which results in the model performing well in prediction performance on the testing set. Thus, the OD sampling technique cannot be applied to the actual prediction.

• 3. SSD sampling technique can ensure that the model training process does not use future information, but the model suffers from significant overfitting problems and has unsatisfactory results on the testing set. SMSSD saves computational efficiency, but the improvement of the model is not obvious compared with that of SSD.

• 4. FSD sampling technique effectively improves the prediction performance of the model while ensuring that the model training process does not use future information. SMFSD dramatically reduces the time consumed for model training because only a single model needs to be trained. Compared with FSD, SMFSD shows better performance in some stations. Considering the performance and efficiency of the models based on FSD and SMFSD sampling techniques, SMFSD may be a better choice, and the VMD can perform better than DWT.

• 5. Compared with the underlying LSTM model, the decomposition-based prediction method may fail to improve the performance of the model substantially, and the performance of the model may be more related to the smoothness and periodicity of the original time series.

• 6. Introducing more features related to the prediction target can further improve the performance of the model effectively.

Notably, decomposition-based forecasting models do not always perform better than single forecasting models, and decomposition forecasting may be a way to try when the model does not work well using single models for forecasting. The major problem faced by decomposition prediction is the boundary distortion in various decomposition methods. The extension of time series may be a direction worth exploring, but whether it can improve the prediction performance of the model is worth further study. Under the premise that boundary distortion is difficult to solve, it is also worth exploring the direction of how to reduce the impact of boundary distortion on model performance, as the idea of FSD and SMFSD, where the unknown information introduced by the boundary distortion is used as part of the model training, and the experimental results also show that this idea effectively improves the performance of the model. In addition, if the time series has strong non-stationarity as well as weak periodicity, we should try to find features that are correlated with the time series as well as to explore the intrinsic temporal characteristics of the time series. Therefore, the performance of multivariate decomposition-based forecasting models can be explored subsequently and different decomposition-based forecasting models can be applied to different datasets in different regions to further validate the applicability of these methods. Furthermore, the research is not only applicable to decomposition-based prediction of streamflow and other hydrological features, but also can be used as a reference for decomposition-based prediction studies in other fields, including but not limited to traffic flow, wind speed, and finance.

Appendix A

DWT

The brief description of the DWT is provided as follows:

• (1) Assume that $x(t)$ is the time series and $K$ is a predetermined decomposition level.

• (2) Calculate the detail term $D^{\prime}_{1}$ and the approximation term $A^{\prime}_{1}$ using the convolution operation.

  $$ D^{\prime}_{1} = x(t) * \alpha^{d} $$

  (5)
  $$ A^{\prime}_{1} = x(t) * \beta^{d} $$

  (6)

  where $\alpha^{d}$ and $\beta^{d}$ denote high-pass and low-pass filters, respectively.

• (3) Down-sample $D^{\prime}_{1}$ and $A^{\prime}_{1}$ to $D^{\prime\prime}_{1}$ and $A^{\prime\prime}_{1}$.

  $$ D^{\prime\prime}_{1} = \{ D^{\prime}_{1} |t = 2,4,6, \cdots \} $$

  (7)
  $$ A^{\prime\prime}_{1} = \{ A^{\prime}_{1} |t = 2,4,6, \cdots \} $$

  (8)

• (4) To carry out a $K$ level decomposition, take the approximation term $A^{\prime}_{m}$ obtained at the $m{\text{ - th}}$ iteration as $x(t)$ in the next iteration. Repeatedly implement steps (2) to (3). Eventually, $K$ detail terms $(D^{\prime\prime}_{1} ,D^{\prime\prime}_{2} , \cdots ,D^{\prime\prime}_{K} )$ and one approximation term $A^{\prime\prime}_{K}$ can be generated.

• (5) Up-sample detail terms and approximation term to $D_{1}^{ * }$, $D_{2}^{ * }$, …, $D_{K}^{ * }$ and $A_{K}^{ * }$.

  $$ D_{m}^{ * } = \left\{ {\begin{array}{*{20}c} {D^{\prime\prime}_{m} (t/2), \, t = {\text{ even number}}} \\ {{ 0 },{\text{ t = odd number}}} \\ \end{array} } \right., \, m = 1,2, \cdots ,K $$

  (9)
  $$ A_{K}^{ * } = \left\{ {\begin{array}{*{20}c} {A^{\prime\prime}_{K} (t/2), \, t = {\text{ even number}}} \\ {{ 0 },{\text{ t = odd number}}} \\ \end{array} } \right. $$

  (10)

• (6) Compute $D_{m}^{ * * }$ and $A_{K}^{ * * }$ using a high-pass filter $\alpha^{u}$ and a low-pass filter $\beta^{u}$.

  $$ D_{m}^{ * * } = D_{m}^{ * } * \alpha^{u} $$

  (11)
  $$ A_{K}^{ * * } = A_{K}^{ * } * \beta^{u} $$

  (12)

• (7) Repeat steps (5) to (6) for $K$ times and use equations (10) and (12) to reconstruct $A_{K}^{ * * }$. Acquire the reconstructed approximation term $A_{K}$ which has the equivalent length as $x(t)$. Then, reconstruct $D_{m}^{ * * }$ by repeatedly implementing steps (5) to (6) for $m$ iterations. Note that at the first iteration equations (8) and (11) are utilized. For the remaining $m - 1$ iterations, equation (12) is modified to be equation (13).

  $$ D_{m}^{ * * } = D_{m}^{ * } * \beta^{u} $$

  (13)

• (8) Finally, acquire the reconstructed detail terms $(D_{1} , \, D_{2} , \, \cdots {\text{, D}}_{K} )$ having the equivalent length as $x(t)$. Summing up all details and approximation terms yields the original time series.

  $$ x(t) = \sum\limits_{i = 1}^{K} {D_{i} + A_{K} } $$

  (14)

EMD

The EMD decomposes a time series into a group of IMFs by following a procedure described below:

• (1) Assume let $s(t)$ be the time series and $x(t)$ the input of the sifting process. Initialize $s(t)$ as $x(t)$.

• (2) Identify all local maxima and minima of $x(t)$. Connect local maxima and minima using the cubic spline interpolation to produce the upper envelope $e_{\max }$ and the lower envelop $e_{\min }$, respectively. Calculate the mean of the two envelops $m(t) = (e_{\max } + e_{\min } )/2$. Extract the detail $d(t) = x(t) - m(t)$.

• (3) Check $d(t)$ against two criteria of the IMF. If they are satisfied, take $d(t)$ as the first IMF $I_{1} (t)$. Otherwise, replace $x(t)$ with $m(t)$ and repeat the step (2) until the first IMF is extracted.

• (4) Repeat steps (2) to (3) by initializing the residual series $R_{n} (t) = s(t) - \sum\nolimits_{i = 1}^{n} {I_{i} (t)}$ as $x(t)$. This sifting process will not terminate at N iteration until a Cauchy-type convergence criterion is satisfied. Eventually, the streamflow series can be described as $s(t) = \sum\nolimits_{i = 1}^{N} {I_{i} (t) + R_{N} (t)}$.

CEEMDAN

In order to eliminate the modal aliasing problem of EMD, CEEMDAN introduces Gaussian white noise with opposite positive and negative into EMD. The specific description of the CEEMDAN algorithm is as follows:

• (1) Suppose the time series is $s(t)$, white noise $\omega^{n} (t)$ with the noise standard deviation $\varepsilon$ is added to the time series $s(t)$, which can be expressed in the following equation:

  $$ s^{n} (t) = s(t) + \varepsilon_{0} \omega^{n} (t),{\text{ n}} = 1,2, \cdots ,K $$

  (15)

  where $K$ represents the number of realizations.

• (2) Performing the decomposition step of EMD on the signal after each realization, and then the first IMF $I_{1} (t)$ is calculated by averaging the components of decomposition.

  $$ I_{1} (t) = \frac{1}{K}\sum\limits_{i = 1}^{K} {I_{1}^{i} (t)} $$

  (16)

• (3) The residual of the first stage is given as: $r_{1} (t) = s(t) - I_{1} (t)$. Then, the signal $r_{1} (t) + \varepsilon_{1} EMD(\omega^{n} (n))$ can be further decomposed by EMD to compute the second IMF mode, and the corresponding residue can also be formulated as follows:

  $$ I_{2} (t) = \frac{1}{K}\sum\limits_{n = 1}^{K} {EMD_{1} (r_{1} (t) + \varepsilon_{1} EMD_{1} (\omega^{m} (t))} $$

  (17)
  $$ r_{2} (t) = r_{1} (t) - I_{2} (t) $$

  (18)

  where $EMD_{K} ( \bullet )$ represents the $k{\text{ - th}}$ IMF mode obtained by the EMD algorithm.

• (4) In the following stage, the $k{\text{ - th}}$ residual and the $k + 1{\text{ - th}}$ component can be computed in the following equation:

  $$ r_{k} (t) = r_{k - 1} (t) - I_{k} (t) $$

  (19)
  $$ I_{k + 1} (t) = \frac{1}{K}\sum\limits_{n = 1}^{K} {EMD_{1} (r_{k} (t) + \varepsilon_{k} EMD_{k} (\omega^{n} (t)))} $$

  (20)

• (5) Repeat Eq. (5)–Eq. (6) until the residue $r_{k} (t)$ satisfies the stoppage criterion:

  $$ \sum\limits_{t = 0}^{T} {\frac{{|r_{k - 1} (t) - r_{k} (t)|^{2} }}{{r_{k - 1}^{2} (t)}}} < SD_{k} $$

  (21)

  where $T$ represents the length of the sequence $s(t)$, $r_{k} (t)$ is the sequence after $k{\text{ - th}}$ decomposition and the empirical value of $SD_{k}$ is set to 0.2. Finally, the original signal $s(t)$ can be decomposed as $s(t) = \sum\nolimits_{m = 1}^{M} {I_{m} (t) + R(t)}$.

VMD

VMD decomposes the signal into $K$ intrinsic mode functions (IMFs) with limited bandwidth and extracts the central frequency of the corresponding IMF, which causes the mode $u_{k}$ to fluctuate around the central frequency $\omega_{k}$. The VMD algorithm can be divided into two processes, namely constructing variational problem and solving variational problem. Meanwhile, VMD solves the bandwidth of each mode, and the variational problem can be written as:

$$ \left\{ {\begin{array}{*{20}c} {\mathop {min}\limits_{{\{ u_{k} \} \{ \omega_{k} \} }} \left\{ {\sum\limits_{{{\text{k}} = 1}}^{K} {\left\| {\partial_{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{\pi t}} \right) * u_{k} \left( t \right)} \right]e^{{ - j\omega_{k} t}} } \right\|_{2}^{2} } } \right\}} \\ {s.t.\sum\limits_{k = 1}^{K} {u_{k} } = f} \\ \end{array} } \right. $$

(22)

where $u_{k}$ is the $k{\text{ - th}}$ IMF with limited bandwidth, $\omega_{k}$ is the corresponding central frequency, and $f$ is the original input signal. By introducing penalty factor $\alpha$ and Lagrangian multiplier $\lambda (t)$, the constrained variational problem is transformed into unconstrained variational problem, which is written as:

$$ \begin{gathered} L\left( {\left\{ {u_{k} } \right\},\left\{ {\omega_{k} } \right\},\lambda } \right) = \alpha \sum\limits_{k = 1}^{K} {\left\| {\partial_{t} \left[ {\left( {\delta \left( t \right) + \frac{j}{\pi t}} \right) * u_{k} \left( t \right)} \right]e^{ - j\omega kt} } \right\|_{2}^{2} } \hfill \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + \left\| {f\left( t \right) - \sum\limits_{k = 1}^{K} {u_{k} \left( t \right)} } \right\|_{2}^{2} + \left\langle {\lambda \left( t \right),f\left( t \right) - \sum\limits_{k = 1}^{K} {u_{k} \left( t \right)} } \right\rangle \hfill \\ \end{gathered} $$

(23)

The alternating multiplication method is used to solve the non-constrained variational problem, namely the minimum point of the extended Lagrange expression can be obtained by alternating and updating $u_{k}$, $\omega_{k}$, and $\lambda$. $u_{k}$, $\omega_{k}$, and $\lambda$ are expressed as follows:

$$ \left\{ \begin{gathered} \widehat{u}_{k}^{n + 1} \left( \omega \right) = \frac{{\widehat{f}\left( \omega \right) - \sum\limits_{i < k}^{K} {\hat{u}_{i}^{n + 1} } (\omega ) - \sum\limits_{i > k}^{K} {\hat{u}_{i}^{n} } (\omega ) + \frac{{\widehat{\lambda }\left( \omega \right)}}{2}}}{{1 + 2\alpha \left( {\omega - \omega_{k}^{n} } \right)^{2} }} \hfill \\ \widehat{\omega }_{k}^{n + 1} = \frac{{\int_{0}^{\infty } \omega \left| {\widehat{u}_{k}^{n + 1} \left( \omega \right)} \right|^{2} d\omega }}{{\int_{0}^{\infty } {\left| {\widehat{u}_{k}^{n + 1} \left( \omega \right)} \right|^{2} d\omega } }} \hfill \\ \hfill \\ \widehat{\lambda }^{n + 1} (\omega ) = \widehat{\lambda }^{n} (\omega ) + \tau (\widehat{f}(\omega ) - \sum\limits_{k = 1}^{K} {\widehat{u}_{k}^{n + 1} (\omega ))} \hfill \\ \end{gathered} \right. $$

(24)

The VMD first divides the frequency band through the characteristics of the original signal; then, each IMF and its corresponding central frequency are continuously updated. Lastly, the adaptive decomposition of the original signal is realized according to the constraint conditions.

LSTM

The basic structure of an LSTM cell is illustrated in Fig.

Fig. 18

LSTM unit structure diagram

18, in which $x_{t}$ is the input vector, $h_{t}$ ($h_{t - 1}$) is the hidden state of the LSTM cell in time step $t$ ($t - 1$), and $c_{t}$ ($c_{t - 1}$) is the cell state of the LSTM cell in time step $t$ ($t - 1$). The structure of the LSTM cell shows that its cell state $c_{t}$ and hidden state $h_{t}$ are transferred to the next time step.

The LSTM cell has three gates (e.g., a forget gate $f_{t}$, an input gate $i_{t}$, and an output gate $o_{t}$) that maintain and adjust its cell $c_{t}$ and hidden states $h_{t}$. The forget gate $f_{t}$ determines what information will be moved away from the cell state $c_{t}$. The input gate $i_{t}$ determines what new information is going to be stored in the cell state $c_{t}$. The output gate $o_{t}$ specifies what information from the cell state is used as output $o_{t}$. In Fig. 3, the cell state $c_{t}$ and hidden state $h_{t}$ of the LSTM cell are calculated as follows:

$$ f_{t} = \sigma (W_{xf} x_{t} + W_{hf} h_{t - 1} + b_{f} ) $$

(25)

$$ i_{t} = \sigma (W_{xi} x_{t} + W_{hi} h_{t - 1} + b_{i} ) $$

(26)

$$ \widehat{c}_{t} = \tanh (W_{xc} x_{t} + W_{hc} h_{t - 1} + b_{c} ) $$

(27)

$$ c_{t} = f_{t} \otimes c_{t - 1} + i_{t} \otimes \widehat{c}_{t} $$

(28)

$$ o_{t} = \sigma (W_{xo} x_{t} + W_{ho} h_{t - 1} + b_{o} ) $$

(29)

$$ h_{t} = o_{t} \otimes \tanh (c_{t} ) $$

(30)

where $\sigma$ is the logistic sigmoidal function, $\otimes$ is the element-wise multiplication of two vectors, and $W_{xi}$, $W_{hi}$, $W_{xf}$, $W_{hf}$, $W_{xo}$, $W_{ho}$, $W_{xc}$, and $W_{hc}$ are the network weights matrices. Similarly, $b_{i}$, $b_{f}$, $b_{o}$, and $b_{c}$ are bias vectors. $f_{t}$, $i_{t}$, and $o_{t}$ are the vectors for the activation values of the forget gate, the input gate, and the output gate, respectively.