Numerical investigation of the effect of geometric parameters on discharge coefficients for broad-crested weirs with sloped upstream and downstream faces

Abstract

Weirs are structures that are important for measuring flow and controlling water levels. Research has shown that the discharge coefficient is not constant and depends on the crest length, the height of the weir, the upstream head, and the upstream and downstream slopes. In this study, the effect of these parameters on the discharge coefficient (C_d) is investigated by numerical simulation. The current study present numerical simulation using the ANSYS FLUENT software. The total number of simulations is 432 which includes: 4 upstream slopes, 4 downstream slopes, 3 weir heights, 3 upstream heads (h₁) and 3 weir crest lengths. It was found that the downstream face slope has little effect on C_d. For 0.1 < H₁/w < 0.4 by decreasing the upstream slope, C_d increases, where H₁ is the water head on the weir crest and w is the length of the crest. Also, for the same range, by decreasing the height of the weir (p), the C_d increases. For 0.16 < H₁/p < 2, as the length of the crest decreases, the C_d increases. By comparing the numerical simulation results to physical measurements, multi-variable regression equations for estimating C_d are presented. In addition to C_d, extraction of other more detailed information such as water level profiles and velocity profiles at different locations is provided.

Introduction

Weirs are hydraulic structures that can be used for flow measurement and water level control in water channels. A wide variety of weir designs have been developed for various applications (Akbari et al. 2019). Based on the thickness of their crests, weirs are classified as sharp-crested (thin-crested) and broad-crested weirs. Sharp-crested weirs have small crest thicknesses. For the broad-crested weir, however, the weir’s crest is very broad compared with other dimensions. With sharp-crested weirs, the water surface is only in contact with the sharp crest of the weir, while for broad-crested weirs, the water flows across the whole thickness of the crest. Sharp-crested weirs are usually classified by their geometric shape which include: rectangular, triangular, trapezoidal, spherical and parabolic shapes (Bos 1989).

There are some advantages for broad-crested weirs compared with other flow measuring structures, such as:

• They can measure discharge. This discharge ranges from 10 cubic feet per second (0.283 cubic meters per second) up to 150 cubic feet per second (4.248 cubic meters per second).

• They are efficient in situations which the channels are wide.

• They are more stable than sharp-crested weirs.

• Broad-crested weirs have high submersion threshold. Submersions up to 80 percent with a vertical downstream face and up to 90 percent with sloped upstream face do not affect the performance of these broad-crested weirs.

• They are often used as dam weirs, especially in gabion weirs and sometimes as the dam itself (if water is allowed to pass over it).

• Broad-crested weirs can be used to store large volumes of water.

• If the upstream face of the weir is sloped, they can easily pass sediments and floating objects (Sargison and Percy, 2009).

One of the disadvantages of broad-crested weirs is the reluctance of farmers and other consumers to install them on their fields. They believe that these structures significantly decrease the flow rate. However, if the weirs are designed correctly, it will not significantly reduce flow (Merkley, 2004). Also, for water that is sediment rich, sediment deposition upstream of the structure (for broad-crested weir with vertical upstream) can occur (Henderson 1966).

Govinda Rao and Muralidhar (1963) divided rectangular weirs into four categories based on their total head (H₁) and weir crest length (w). The classifications are: rectangular long-edged weirs ($0 < \frac{{H_{1} }}{w} < 0.1$), rectangular broad-crested weirs ($0.1 < \frac{{H_{1} }}{w} < 0.4$), rectangular short-crested weirs ($0.4 < \frac{{H_{1} }}{w} < 1.5$), and rectangular sharp-crested weirs ($1.5 < \frac{{H_{1} }}{w}$). Singer (1964) showed that by changing the height (p) and the length of the crest of weir (w), the discharge coefficient varies.

Hager and Schwalt (1994) studied broad-crested weirs with vertical walls. They installed a number of piezometers to measure pressure. Some were installed on the surface of upstream vertical wall, and others were installed on horizontal part of the weir. One of the significant results obtained by Hager and Schwalt (1994) was a sudden drop in the downstream water level at low discharge. While in high discharge, the flow level upstream decreased gradually and increased downstream flow level.

Fritz and Hager (1998) obtained discharge coefficients and flow data for broad-crested weirs with 2:1 (vertical: horizontal) slopes. They showed that flow separation decreases in the presence of a slope. Johnson (2000) showed that discharge coefficient for both broad-crested and sharp-crested weirs for $\frac{{H_{1} }}{w} < 0.2$ collapsed to a single curve where H₁ is the upstream head and w is the length of weir crest.

Farhoudi and Shah Alami (2005) studied the effects of the upstream face slope of a broad-crested weir; they reported that by decreasing the upstream face slope, its discharge coefficient increased. They recommended a 25° slope of the upstream face.

Gogus et al. (2006) made experiments on rectangular broad-crested weirs with compound cross-sections. These weirs have one small rectangular part that is used to transfer low discharges, and another rectangular part with a larger width. Compound cross-section (the combination of two different parts) is used to transfer higher discharge rates. The study of rectangular broad-crested weirs with compound cross-sections was also provided in Salmasi et al. (2013). There, laboratory data were used to measure the discharge and estimations were found using a Genetic Algorithm (GA).

Farhoudi and Shokri (2007) evaluated the effects of the downstream face slope on discharge coefficients. They showed that the downstream face slope has negligible effect on the discharge coefficient and to reduce the potential of cavitation, a vertical slope is preferred. Gonzalez and Chanson (2007) made experiments on broad-crested weirs and evaluated velocity and pressure distribution profiles on a sharp-edged broad-crested weir. Results showed that upstream of the weir, spiral vortex flows are created. Using dimensional analysis, they found that the creation and the strength of these vortex flows are related to the weir relative height ($\frac{{H_{1} }}{P}$), weir relative width ($\frac{B}{P}$) and Reynolds number ($\frac{Q}{{B_{v} }}$). The symbol H₁ is the upstream head, p is the height of weir, B is the width of weir, Q is the transfer discharge over the weir, and υ is kinematic viscosity.

Sargison and Percy (2009) made physical models of rectangular broad-crested weirs with different upstream and downstream slopes and showed that downstream slope has negligible effect on discharge coefficients. On the other hand, as the upstream slope gets smoother, discharge coefficients increase. Bijankhan et al. (2013) examined flow over weirs with different crest lengths and heights in order to obtain a single correlating formula with dimensionless parameters $\frac{w}{P}$ and $\frac{{K_{s} }}{P}$ for rectangular weirs (long-crested, broad-crested, short-crested and sharp-crested weirs). The key result of their study is the following equation which can be used with less than 4% error.

$$\frac{{h_{1} }}{w} = 1.4404\left( \frac{w}{P} \right)^{ - 0.97} \left( {\frac{{K_{s} }}{P}} \right)$$

(1)

Here h₁ is the upstream head, w is the length of the weir, P is the height of weir, and K_s is the critical depth.

Hosseini and Afshar (2014) performed experiments on two models of rectangular broad-crested weirs with different lengths in order to evaluate discharge coefficients. Their results showed that the dimensionless parameter $\frac{{H_{1} }}{B}$ (H₁ is the upstream head and B is the weir width) is not negligible for determining discharge coefficients. Furthermore, with increasing water depth on the weir’s crest, the discharge coefficient increased slightly, a finding that is consistent with the results of previous studies.

Moradi et al. (2020) used laboratory models to investigate the effect of the upstream face slope of a rectangular broad-crested weir on the discharge coefficient and water level profile. The results showed that the decrease in upstream face slope inhibits the development of flow separation. They found that reducing the upstream face slope to 21 degrees increased the discharge coefficient by up to 10 percent and reduced the relative length and height of the separation region by 80 and 95 percent, respectively.

Jiang et al. (2018) numerically examined flow on a broad-crested weir with a sloping upstream face. They showed that there is an inverse relationship between the discharge coefficient and the upstream slope; as the upstream slope decreases, the discharge coefficient increases. Moreover, when the upstream slope exceeds 60 degrees, cavitation occurs, and with increasing slope, cavitation increases.

Yildz et al. (2020) modeled a broad-crested weir both experimentally and numerically using ANSYS FLUENT software and presented the following formula for the discharge coefficient. They found that the size of the structure has an effect on the critical depth formation.

$$C_{wd} = \frac{0.65}{{\sqrt {1 + \frac{{H_{1} }}{p}} }}$$

(2)

Moradi et al. (2020) studied broad-crested gabion weirs with upstream and downstream sloping faces and concluded that with increasing relative depth $\frac{{y_{2} }}{{y_{1} }}$ (the terms y₁ and y₂ are, respectively, the water depths upstream and downstream) the discharge reduction factor (${\uppsi }$) decreases in free flow with a smooth slope. On the other hand, with a submerged flow, this downward slope becomes steeper, and with increasing upstream and downstream slopes the discharge reduction factor increases. There is a recent study Salmasi et al. (2021) in which rectangular broad-crested gabion weir discharge coefficients were investigated in free and submerged flow conditions. They presented regression relations for estimating discharge coefficients in these types of weirs.

Zerihun (2020) made an experimental evaluation of discharge coefficients for trapezoidal broad-crested weirs and compared their results with Fritz and Hager (1998) and Sargison and Percy (2009). They concluded that upstream and downstream faces are effective for modifying discharge coefficients of broad-crested weirs. They also presented the following relation with a 1.11% root mean square error (RMSE):

$$C_{d} = 0.4 - 0.215\left( {\sin \theta } \right)^{{\frac{22}{{125}}}} + 0.13\left( {\sin \varphi } \right)^{\frac{3}{20}} + \frac{0.134\zeta }{{1 + 0.596\zeta }}$$

(3)

$$\zeta = \frac{{H_{0} }}{L}$$

where H₀ is the weir upstream head, L is the length of the weir crest, θ is the angle of the upstream slope, and φ is the angle of the downstream slope.

The current study present numerical simulation using the ANSYS FLUENT software. These numerical simulations are carried out to find C_d for broad-crested weirs in irrigation canals. Broad-crested weirs with upstream and downstream face slopes are considered as well as conventional vertical faces. Validation is based on a comparison of the simulations with experimental results. In addition, flow details such as pressure fields and velocity vectors are used for comparing different geometrical shapes. The novelty of present study relates to full consideration of all geometrical parameters of rectangular broad-crested weir for estimation of C_d. These parameters include: upstream slopes (z₁), downstream slopes (z₂), weir heights (p), upstream heads (h₁) and weir crest lengths (w).

Material and methods

Geometrical dimensions of broad-crested weirs

The free flow over the broad-crested weir is simulated by ANSYS FLUENT in 2D. By changing geometrical parameters (upstream slope, downstream slope, height, crest length and upstream head), the variation of discharge coefficients and velocity and pressure profiles can be obtained.

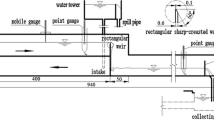
In Fig. 1, the longitudinal cross-section of the rectangular broad-crested weir and hydraulic parameters are illustrated. In Table 1, the geometrical properties of broad-crested weirs are listed. The total number of simulations is 432 which includes: 4 upstream slopes, 4 downstream slopes, 3 weir heights, 3 upstream heads (h₁) and 3 weir crest lengths.

Fig. 1

Geometrical and hydraulic parameters of the broad-crested weir

Table 1 Geometrical properties of broad-crested weirs in this study

Accuracy evaluation indicators

Three statistical indicators have been used to evaluate the accuracy of ANSYS FLUENT simulations in comparison with the available experimental data. These indicators are: determination coefficient (R²), root mean square error (RMSE) and percent relative error (RE%) which can be calculated by the following:

$$R^{2} = \frac{{\left[ {\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \overline{O}} \right)\left( {P_{i} - \overline{P}} \right)} \right]^{2} }}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {O_{i} - \overline{O}} \right)^{2} \mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - \overline{P}} \right)^{2} }}$$

(4)

$$RMSE = \sqrt {\frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {P_{i} - O_{i} } \right)^{2} }}{n}}$$

(5)

$$RE\% = \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\left| {P_{i} - O_{i} } \right|} \right)}}{{\mathop \sum \nolimits_{i = 1}^{n} P_{i} }}$$

(6)

where O_i are the discharge coefficients that result from numerical simulation, P_i are the experimental results, terms with an over bar are mean values, and n is number of data.

Dimensional analysis

There may be many parameters that can affect discharge coefficients. In fact, the number of potential parameters results in a very large number of parameter collections. However, with dimensional analysis, the number of independent inputs can be reduced. The effective parameters in this study are shown in Eq. 7.

$$f\left( {H_{1} ,w,\rho ,p,L,Q,g,\mu ,z_{1} ,z_{2} } \right) = 0$$

(7)

By using the Buckingham π theorem, dimensionless quantities are obtained as follows:

$$f^{\prime}\left( {\frac{{H_{1} }}{w},\frac{{H_{1} }}{p},\frac{L}{p},\frac{{\rho g^{\frac{1}{2}} H_{1}^{\frac{3}{2}} }}{\mu },\frac{Q}{{g^{\frac{1}{2}} H_{1}^{\frac{5}{2}} }},z_{1} ,z_{2} } \right) = 0$$

(8)

$$\frac{Q}{{g^{\frac{1}{2}} H_{1}^{\frac{5}{2}} }} = f^{\prime}\left( {\frac{{H_{1} }}{w},\frac{{H_{1} }}{p},\frac{L}{p},\frac{{\rho g^{\frac{1}{2}} H_{1}^{\frac{3}{2}} }}{\mu },z_{1} ,z_{2} } \right)$$

(9)

The dimensionless parameters in Eq. (9) include geometric, kinematic, and dynamic properties. The geometric quantities are: weir height (p), weir length (w) and weir crest width (L). The kinematic properties include flow discharge (Q) and total head upstream of the weir (H₁). Dynamic properties are gravitational acceleration (g), dynamic viscosity (μ), and specific mass of water (ρ).

In Eq. (9), the dimensionless term $\frac{{\rho g^{\frac{1}{2}} H_{1}^{\frac{3}{2}} }}{\mu }$ is the efficacy indicator of the viscous force and is equal to the ratio of Reynolds number (R_e) to Froude number (F_r).

$$\frac{{{\text{Re}}}}{{{\text{Fr}}}} = \frac{{\rho g^{\frac{1}{2}} H_{1}^{\frac{3}{2}} }}{\mu }$$

(10)

For a particular fluid, the values of g, ρ, and μ are given and therefore we find R_e and F_r as a function of H₁. Consequently, Eq. (9) can be written in the simplified form of Eq. (11).

$$\frac{Q}{{g^{\frac{1}{2}} H_{1}^{\frac{5}{2}} }} = f^{\prime}\left( {\frac{{H_{1} }}{w},\frac{{H_{1} }}{p},\frac{L}{p},z_{1} ,z_{2} } \right)$$

(11)

The generalized flow-discharge coefficient relation of rectangular broad-crested weirs can also be written as:

$$Q = C_{d} \frac{2}{3}L\sqrt {2g} H_{1}^{\frac{3}{2}}$$

(12)

By comparing the right-hand side of Eq. (11) with a generalized equation of rectangular broad-crested weirs (Eq. (12)), we find that the two equations can be rewritten as

$$C_{d} = f^{\prime}\left( {\frac{{H_{1} }}{w},\frac{{H_{1} }}{p},\frac{b}{p},z_{1} ,z_{2} } \right)$$

(13)

By considering variable factors of this study, the final Eq. (14) is presented.

$$C_{d} = f^{\prime}\left( {\frac{{H_{1} }}{w},\frac{{H_{1} }}{p},z_{1} ,z_{2} } \right)$$

(14)

Numerical simulation using the finite volume method (FVM)

A common method for investigating flow over weirs is to construct a small-scale physical model of them. Fabricating of physical models often requires extensive time and cost for construction. These hurdles have motivated the use of numerical models. The use of computer models for flow investigation in hydraulic structures has become widespread with the development of numerical methods that can handle the coupled nonlinear equations of fluid flow. In this study, a numerical model was used to investigate the hydraulic properties of the flow over broad-crested weirs with different geometries. The method of this numerical study is as follows:

In a Cartesian coordinate system, flow can be described using the incompressible continuity principle (Eq. 15) along with the Reynolds-Averaged Navier–Stokes (RANS) equation (Eq. 16):

$$\frac{\partial }{{\partial x_{i} }}\left( {\overline{{u_{i} }} } \right) = 0$$

(15)

$$\rho \left( {\frac{{\partial \overline{{u_{i} }} }}{\partial t} + u_{j} \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }}} \right) = \overline{{f_{i} }} - \frac{{\partial \overline{P}}}{{\partial x_{i} }} + \frac{\partial }{{\partial x_{j} }}\left( {\mu \frac{{\partial \overline{{u_{i} }} }}{{\partial x_{j} }} - \rho \overline{{u_{i}^{^{\prime}} u_{j}^{^{\prime}} }} } \right)$$

(16)

where ${ }\overline{{u_{i} }}$ and $\overline{{u_{j} }}$ are average velocity components, m/s; x_i and x_j are Cartesian coordinate axes; $\overline{{f_{i} }}$ is the body force, m/s²; p is pressure, N/m²; $- \overline{{\rho u_{i}^{^{\prime}} u_{j}^{^{\prime}} }}$ is the Reynolds stress term, which needs to be modeled using a turbulence model (Jiang et al., 2018). Turbulence models are classed into: algebraic (zero-equation), one-equation, two-equation, and stress-transport models (Wilcox, 1993). The models have also been divided into the following classes: k–ε model (standard k–ε model, renormalization group (RNG) k–ε model and realizable k–ε model) and k–ω model (standard k–ω and shear stress transport (SST) k–ω). The five turbulence aforementioned models are solved using the ANSYS FLUENT software package (Nourani et al. 2021). In order to identify the most relevant turbulence model in present study, the models were evaluated with experimental data from a previous study and the best one was selected.

Flow over a broad-crested weir is a typical air–water two-phase flow. The present study uses a powerful computational tool for analyzing free surface flow. This analysis is carried out using the volume of fluid (VOF) algorithm developed by Hirt and Nichols (1981). In this approach, a volume fraction α is used to define the portion of each mesh cell occupied each fluid. The value of α ranges from zero to one (0 $\le$ α $\le$ 1). When α equals 1, it indicates that the cell is full of water while when the term is 0, the cell is full of air. For 0 < α > 1, a fraction of the cell is filled with water. Therefore, the free surface over the water flow can be determined by cells with α < 1. In this study, the interface occurs when α equals 0.5 (Toro et al. (2017); Bayon et al. (2016)). The value of α in each cell is computed through Eq. (17)

$$\frac{\partial }{\partial t}\left( \alpha \right) + u_{i} \frac{\partial }{{\partial x_{i} }}\left( \alpha \right) + u_{j} \frac{\partial }{{\partial x_{j} }}\left( \alpha \right) = 0$$

(17)

Constructing the geometry of the model

The two-dimensional model had a fixed width of 10 m. The laboratory setup of Sargison and Percy (2009) was used; the flume length is 6 m and the weir was placed 2 m upstream.

At the inlet, a velocity was applied. At all fluid–wall interfaces, no-slip conditions were used. At the water–air interface, symmetry conditions were applied and an outlet boundary conditions was used at the downstream end of the solution domain.

With respect to the mesh, a total of 3635 elements were used and the orthogonal quality of the elements was excellent, ranging from 0.7 to 1. The computational mesh is shown in Fig. 2.

Fig. 2

The computational mesh

The k–ε, RNG turbulence model was used. An implicit iterative solver was used to obtain the converged results. Fluent uses the control-volume method wherein the governing equations are integrated over each control volume. The PRESTO method was used for the pressure interpolation scheme. In order to couple pressure and velocity, the SIMPLEC algorithm was used. The SIMPLEC design uses a segregated algorithm and is appropriate for multiphase models. This approach is advantageous compared to other methods (such as the SIMPLE algorithm) and results in accelerated convergence of the governing equations (Salmasi and Samadi, 2018).

The hydraulic diameter is calculated in following relation:

$${\text{D}} = 4{\text{R}} = 4 \times \frac{A}{P}$$

(18)

where A is the flow cross-section and P is the wetted perimeter. The Reynolds number is calculated by Eq. (19).

$${\text{Re}} = \frac{VD}{{\upsilon }}$$

(19)

where V is the flow velocity, D is the hydraulic diameter, and ν is the kinematic viscosity. Finally, turbulence intensity is calculated by Eq. (20).

$$I = 16{\text{Re}}^{{\frac{ - 1}{8}}}$$

(20)

Execution is carried out using an unsteady solver. The number of time steps was set to 1000, and the time step size was 0.01 s. The maximum number of iterations for each time step was 100.

Sargison and Percy (2009)’s laboratory results were used for validation. They used Eq. (21) to calculate discharge coefficients for broad-crested weirs.

$$C_{d} = 0.43 + 0.06\sin \left[ {\pi \left( {\varepsilon - 0.55} \right)} \right] - 0.039\theta + 0.0029$$

(21)

where θ is the upstream face slope in radians and є is the relative length of the crest that is equal to $\varepsilon = \frac{{H_{1} }}{{H_{1} + w}}$.

Table 2 provides the domain of experimental dimensionless parameters in this study. With combination of these parameters, the total number of numerical simulations is 432.

Table 2 The values of dimensionless parameters

Results and discussion

Numerical simulations

In Fig. 3a–c, the water level profiles are provided for conditions where the upstream face slope angle (z₁) is equal to 30 degrees, the downstream face slope angle (z₂) is equal to 60 degrees, the length of the weir crest (w) is 0.85 m, and the upstream head (H₁) is 0.2 m. The multipart figure shows results for three weir heights (p) of 0.1, 0.2, and 0.3 m. The results show that the flow discharge for these three heights is 0.225, 0.188, and 0.170 m³/s, respectively. Therefore, it can be seen that the weir height has a significant role on flow condition, and as the weir height decreases, the discharge rate increases. For example with 100% increase in weir height (p) from 0.1 to 0.2 m, the discharge shows a reduction of 84%; with 200% increase in p from 0.1 to 0.3 m, the discharge shows a reduction of 76%.

Fig. 3

Water level profiles for broad-crested weirs with upstream and downstream sloped faces and for different weir heights

In Fig. 4a–c, the results for flow over a broad-crested weir for three situations are shown, including: a sloped upstream face and a vertical downstream face, a vertical upstream face and a sloped downstream face, and a sloped upstream and downstream faces for weir heights of 0.1, 0.2 and 0.3 m, weir crest lengths of 0.5, 0.85 and 1 m and upstream heads of 0.05, 0.15 and 0.2 m.

Fig. 4

a, b and c: Velocity contours on the broad-crested weir for three different face slope scenarios

Figure 4a shows the flow velocity profile where the upstream face slope angle (z₁) is 60 degrees, the downstream face slope angle (z₂) is 90 degrees, weir height (p) is 0.2 m, weir crest length (w) = 0.5, and upstream head (H₁) was 0.2 m. The flow velocity was calculated to be 0.72 m/s. In Fig. 4b, flow velocity contours are shown for an upstream face slope of 90 degrees, a downstream face slope of 30 degrees, a weir height of 0.2 m, weir crest length of 0.85 m, and upstream head of 0.2 m. For this situation, the resulting velocity is 0.65 m/s. The final set of results, shown in Fig. 4c, corresponds to an upstream slope of 60 degrees, downstream slope of 30 degrees, weir height of 0.2 m, weir crest length of 0.85 m, and upstream head of 0.2 m. The resulting velocity was calculated to be 0.74 m/s.

By comparing the results of three Fig. 4a–c, it can be shown that the upstream face slope has a significant effect on velocity while downstream slope has little effect. According to Sargison and Percy (2009), in order to reduce downstream separation, 90 degrees is preferred. Based on this observation, an upstream slope of 15 degrees and a downstream slope of 90 degrees are optimal. In fact, the milder upstream slope results in a smoother transition of flow lines toward weir crest. In this condition, the separation zone on the weir crest reach is minimal and lower energy loss happens. At downstream locations, because of the difference between tail water elevation with water surface on the weir crest, downstream slope shows lower effect on flow discharge. Therefore, the downstream slope does not show a significant effect on discharge and a vertical downstream slope will be a proper geometry.

Figure 5 provides velocity vectors for flow over broad-crested weirs with different upstream and downstream slopes. The velocity vectors in Fig. 5 show that the flow velocity near the channel bed is low and then gradually increases. Then, near the water surface, the flow velocity decreases again. It should be noted that the length of the vectors indicates the magnitude of the velocity. In the zoomed areas, more local detail of flow direction and velocity is provided. It can be seen that with an upstream slope of 15 degrees (Fig. 5a) the velocity vectors are more regular and the resistance is lower. These facts increase C_d. But in the weir with an upstream slope of 60 degrees (Fig. 5b), more irregular velocity vectors are seen.

Fig. 5

Velocity vectors for flow over broad-crested weirs including upstream and downstream slope faces

In Figs. 6, 7 and 8, the discharge coefficient versus the ratio of upstream head to crest length of broad-crested weirs (H₁/w) is shown. The results correspond to upstream slopes of 90, 60, 30 and 15 degrees, downstream slopes of 90, 60, 30 and 15 degrees, and weir heights of 0.1, 0.2 and 0.3 m. As can be seen, for ${0}{\text{.1}} < \frac{{H_{1} }}{w} < 0.4$, by decreasing the height of the weir under certain conditions, the upstream head increases slightly, and as a result, the discharge coefficient increases. By decreasing the upstream slope, the flow separation in the upstream corner of the overflow decreases and this causes the discharge coefficient to increase. It is also seen that the downstream slope has little effect on the discharge.

Fig. 6

Discharge coefficients for z₁ = 90°, z₂ = 30° and various weir heights

Fig. 7

Discharge coefficients for z₁ = 30°, z₂ = 60° and various weir heights

Fig. 8

Discharge coefficients for z₁ = 15°, z₂ = 90° and various weir heights

The differences in discharge coefficients displayed in Figs. 5, 6 and 7 reveal that the largest coefficients occur at the lowest weir height for the same hydraulic conditions and face slopes.

In Fig. 9, the discharge coefficient with respect to dimensionless ratio H₁/w is displayed. The highest discharge coefficient occurs with a weir upstream slope that is equal to 15 degrees.

Fig. 9

Discharge coefficients for z₂ = 15°, p = 0.1 m and for different upstream slopes

In Figs. 10, 11, 12, discharge coefficient versus H₁/p for the broad-crested weir with upstream slopes of 90, 60, 30 and 15 degrees and downstream slopes of 90, 60, 30 and 15 degrees are shown. There are three weir crest lengths (0.5, 0.85, and 1 m). For values of 0.16 $< \frac{{H_{1} }}{P} < {2 }$, decreases in crest length cause an increase in the discharge coefficient. By decreasing the slope of the upstream face, the discharge coefficient increases.

Fig. 10

Discharge coefficients for z₂ = 90°, w = 1 m and various upstream slopes

Fig. 11

Discharge coefficients for z₂ = 60°, w = 0.85 m and various upstream slopes

Fig. 12

Discharge coefficients for z₁ = 15°, z₂ = 90° and various crest lengths

Figure 13 provides the discharge coefficient as a function of z₁ and z₂ for similar hydraulic conditions. In Fig. 13a, it can be seen that by decreasing the upstream face slope, the discharge coefficient increases. A 50 percent decrease in the upstream slope leads to a 4 percent increase in the discharge coefficient. The downstream slope has a lesser effect on the discharge coefficient.

Fig. 13

Discharge coefficient as a function of z₁ and z₂

Extraction of regression relationships using SPSS software

SPSS software was used to connect dimensionless parameters H₁/p, H₁/w, z₁ and z₂ to the discharge coefficient and regression relations were extracted (Eq. 21). These relations can be used to determine discharge coefficients. The values of R², RMSE and % RE for Eq. (22) are 0.954, 0.05 and 0.02%, respectively. It should be noted that the negative upstream slope coefficient (z₁) means there is an inverse relationship between the upstream face slope and the discharge coefficient.

$$C_{d} = - 0.178z_{1} + 0.005z_{2} + 0.431\frac{{H_{1} }}{p} + 0.084\frac{{H_{1} }}{w} + 1.085$$

(22)

Next, a data scatter diagram is provided (Fig. 14) which includes 252 data points. As can be seen, most of the data are scattered near the bisector of the first quarter (y = x), which shows the accuracy of the relation in estimating the discharge coefficients.

Fig. 14

Scatter plot of obtained discharge coefficients obtained from of Fluent and Eq. (22)

Next, candidate nonlinear regression equations were developed to connect the drag coefficient to the independent variables. The first nonlinear regression relationship was obtained using SPSS software and is shown in Eq. (23). Accuracy criteria R², RMSE and RE% are 0.9628, 0.07 and 4%, respectively. A scatter plot using Eq. (23) is provided in Fig. 15. Results show that nonlinear Eq. 23 is superior to the linear model set forth in Eq. 22.

$$C_{d} = 161.473 - 0.182\left( {z_{1} } \right)^{0.978} + 0.072\left( {z_{2} } \right)^{0.072} - 160.295\left( {1 + \frac{{H_{1} }}{w}} \right)^{ - 0.001} + 0.293\left( {\frac{{H_{1} }}{p}} \right)^{1.403}$$

(23)

Fig. 15

Scatter plot of discharge coefficients obtained from of Fluent and Eq. (23)

A third correlating model was generated, as shown in Eq. (24). Accuracy criteria R², RMSE and RE% were calculated to be 0.94, 0.06 and 0.56%, respectively. A scatter plot is provided in Fig. 16; results show that nonlinear Eq. 24 is performed similarly to Eq. (22).

$$C_{d} = 0.982 + 0.42z_{1}^{ - 0.253} z_{2}^{0.007} \left( {\frac{{H_{1} }}{w}} \right)^{0.105} \left( {\frac{{H_{1} }}{p}} \right)^{1.068}$$

(24)

Fig. 16

Scatter plot of discharge coefficients obtained from of Fluent and Eq. (24)

A fourth correlating model was developed, as shown in Eq. (25). The error measurements R², RMSE and RE% were 0.978, 0.132 and 0.37%, respectively. A scatter plot is provided in Fig. 17; results show that nonlinear Eq. 25 is not superior to the two nonlinear models of Eqs. (23) and (24).

$$C_{d} = \frac{{0.124 + 0.047z_{1}^{1.286} + 0.881z_{2}^{0.22} + 12.504\left( {\frac{{H_{1} }}{w}} \right)^{6.960} + 0.188\left( {\frac{{H_{1} }}{p}} \right)^{2.213} }}{{ - 0.547 + 0.132z_{1}^{1.345} + 0.009z_{2}^{1.708} + 1.289\left( {\frac{{H_{1} }}{w}} \right)^{ - 0.027} + 3.438 \times 10^{ - 7} \left( {\frac{{H_{1} }}{p}} \right)^{18.625} }}$$

(25)

Fig. 17

Scatter plot of discharge coefficients obtained from of Fluent and Eq. (25)

Figure 18 compares the results of the present study with Sargison and Percy (2009) for 100 data points and for $z_{1} = 30^\circ$, w = 0.5 m and p = 0.25 m. As can be seen, the numerical simulations in the present study provide close agreement to the laboratory results of Sargison and Percy (2009). Valves of R², RMSE and RE% are 0.7135, 0.104 and 2.5%, respectively.

Fig. 18

Comparison of the present numerical simulation results to laboratory results of Sargison and Percy (2009)

Bijankhan et al. (2013) used experimental surveys to present discharge coefficient relation in the form of Eq. (26).

$$C_{d} = 4.2003\left( {\frac{h}{h + P}} \right)^{2} - 2.5966\left( {\frac{h}{h + P}} \right) + 1.3563$$

(26)

Figure 19 shows the comparison between the results of the present study and the research conducted by Bijankhan et al. (2013) for 100 data with similar conditions. The values of R², RMSE and RE% from this comparison are 0.8602, 0.139 and 10%, respectively. It seems that for C_d > 1.25 there is a better accordance between numerical simulations of this study and laboratory results of Bijankhan et al. (2013).

Fig. 19

Comparing the numerical simulation results in present study and laboratory results of Bijankhan et al. (2013)

By using laboratory tests, Zerihun (2020) presented Eq. (27) to estimate discharge coefficient.

$$C_{d} = 0.4 - 0.215\left( {\sin \theta } \right)^{{\frac{22}{{125}}}} + 0.13\left( {\sin \varphi } \right)^{\frac{3}{20}} + \frac{0.134\zeta }{{1 + 0.596\zeta }}$$

(27)

$$\left( { \zeta = \frac{{H_{0} }}{L}} \right)$$

Figure 20 shows the comparison of the present study with Zerihun (2020). The values of R², RMSE and% RE are 0.72, 0.094 and 5%, respectively.ζ

Fig. 20

Comparison of the present numerical simulations results to the laboratory results of Zerihun (2020)

Conclusions

In this study, changes in discharge coefficient for broad-crested weirs were investigated. The independent variables included upstream slope, downstream slope, crest length, crest height and head on the crest. Numerical simulation method was employed using ANSYS FLUENT software. An attempt was made to test different multivariate regression equations for discharge coefficients (dependent variable) and other variables (independent variables). Then, the discharge coefficients obtained in the simulated broad-crested weirs were compared with the laboratory data of Sargison and Percy (2009); Bijankhan et al. (2013); Zerihun (2020). Some important results are as follows:

Considering the relative error percentage in comparison with the laboratory data, it is concluded that FLUENT software simulates the flow on broad-crested weirs with high accuracy. In this study, the highest discharge coefficient occurs for weir with conditions z₁ = 15°, z₂ = 30°, p = 0.1 m, w = 0.5 m and H₁ = 0.2 m and the lowest discharge coefficient occurs for weir with conditions z₁ = 90°, z₂ = 15°, p = 3 m, w = 0.5 m and H₁ = 0.05 m. For values of 0.1 $< \frac{{H_{1} }}{w} < {0}{\text{.4}}$, the discharge coefficient increases with decreasing height and with decreasing upstream slope. Downstream slope has little effect on the flow discharge coefficient. For values of $0.16 < \frac{{H_{1} }}{p} < 2$, the discharge coefficient increases with decreasing the length of the crest and C_d increases with decreasing upstream slope. Numerical simulations showed better agreement with Bijankhan et al. (2013)’s study than the others. The values of R², RMSE and RE% from this comparison are 0.8602, 0.139 and 10%, respectively. Among different tested multiple regression equations, nonlinear Eq. (22) is preferred for prediction of C_d. Accuracy criteria R², RMSE and RE% were calculated to be 0.94, 0.06 and 0.56%, respectively.