Introduction

Groundwater is the most important source of water supply in many countries, and its improper use, industrial and agricultural development, and human population growth have led to a significant reduction in these water resources (Burns et al. 2005; Wada et al. 2010; Shivasorupy et al. 2012; Motevalli et al. 2019; Sahour et al. 2020). On the other hand, the natural recharge ​​of groundwater due to precipitation and surface water resources has decreased due to climate changes and increased withdrawal of surface water resources. Intensification of this trend can be considered a serious threat to human life. Therefore, it is necessary to plan for managing groundwater resources and the risk of dropping groundwater depth (Abulibdeh et al. 2021).

Piezometry wells are used to study the quantity and quality of groundwater. Unfortunately, the number of piezometric wells for groundwater studies in underdeveloped countries such as Iran is limited, and generally, the statistical period of the wells is limited. Further, drilling wells and performing necessary sampling is time-consuming and costly. Therefore, it is appropriate to use efficient methods to estimate the groundwater depth fluctuations ​​in the plains. In the last decade, one of the common methods that have been considered in the process of modeling groundwater is the use of artificial intelligence methods. Various methods of artificial intelligence including artificial neural networks (ANNs), self-organizing maps (SOMs), fuzzy neural networks, and learning machines have been widely used in the study of groundwater resources.

A fuzzy neural network is one of the efficient methods in modeling hydrological parameters that combines the capabilities of neural network and fuzzy system. A fuzzy neural network is a learning machine that finds the fuzzy system parameters (i.e., fuzzy rules, fuzzy sets) by using approximation techniques from neural networks. From fuzzy neural networks in groundwater quality studies and groundwater depth studies has been widely used. The fuzzy neural network is also used efficiently in the process of hydrological modeling with a combination of neural network capabilities and fuzzy system (Chang and Chen 2001; Dixon 2005; Vernieuwe et al. 2005; Jacquin and Shamseldin 2006; Chang and Chang 2006; Cobaner et al., 2009; Zhang et al. 2009; Dogan et al. 2010; Liu et al. 2010; Kisi 2010; Mirbagheri et al. 2010; Gharibi et al. 2012; Karimi-Googhari 2012; Loganathan and Girija 2013; Ullah and Choudhury 2013; Son and Kim 2018; Castiello et al. 2019; Gezahegne Tiruneh et al. 2020; Kannadasan et al. 2020; Vitorde and Souza 2020).

Awasthi et al. (2005) applied a fuzzy logic model for modeling groundwater recharge and they simulated groundwater fluctuations and the groundwater recharge values. Lohani et al. (2012) used adaptive neuro-fuzzy, neural network, and autoregressive techniques in hydrological time series modeling. They found that neuro-fuzzy has a higher performance than the neural network in the modeling process. Moreover, neuro-fuzzy was used for simulating groundwater quality and that can be used for classifying drinking water quality (Wang et al. 2014). Memarian et al. (2016) used a co-active neuro-fuzzy inference system (CANFIS) for predicting droughts in Iran. Their results showed that the CANFIS network can predict the duration and severity of droughts with acceptable accuracy. Allawi et al. (2018) simulated reservoir inflow of a dam using a modified CANFIS network in a semiarid region. Their results showed that the CANFIS network can simulate the reservoir inflow with high performance. Pradhan et al. (2018) used the CANFIS network to model groundwater depth in an Indian interbasin. Their results showed that the CANFIS network and groundwater withdrawal values can be used in estimating groundwater drawdown.

A geographic information system (GIS) is a system for saving data, data processing and analyzing, and mapping the geo-referenced data. The GIS can be used as an efficient tool in the model running and mapping in groundwater studies. Past studies indicate the high performance of combining artificial intelligence and GIS capabilities in modeling the quantity and quality of groundwater (Ganapuram et al. 2009; Bradai et al. 2016; Delsman et al. 2018; Haselbeck et al. 2019; Abulibdeh et al. 2021).

Groundwater depth fluctuations and water table drawdown are important problems in water resources management. Several studies have been done in groundwater depth modeling. But, the estimate of annual groundwater depth drawdown has received less attention because it requires data on groundwater withdrawal values and is difficult and complex to estimate.

In the present study, the annual groundwater drawdown in an unconfined aquifer by using the neural fuzzy network and GIS is simulated. The CANFIS network can be an efficient method to simulate groundwater depth fluctuations, and the GIS can be used as an efficient tool in mapping the results of model simulation. By combining them, the modeling process is performed in a short time and with high performance, and the results are presented as geo-referenced data. Moreover, the spatial variation of annual groundwater drawdown on the southern Caspian coasts is simulated. The aim of this study is to model the annual values ​​of groundwater drawdown in the alluvial aquifers and to prepare a map of groundwater depth drawdown values ​​by using a neural fuzzy network and the GIS.

Materials and methods

Study area

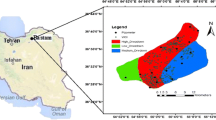
The study plain with an area of ​​10,000 square kilometers in the north of Iran is located on the southern coasts of the Caspian Sea in the range of east longitude 50° 34′ to 54° 10′ and north latitude 35° 47′ to 37° (Fig. 1). The mean annual precipitation decreases from west to east and annual precipitation varies from 1300 mm in the west to 600 mm in the east of the plain. Studies have been performed on an unconfined aquifer in Quaternary alluvial formations. The minimum depth of groundwater is observed on the Caspian coasts (1 m) and the maximum is recorded near the mountains (40 m). Different land uses are observed including agricultural lands (paddy fields and gardens), residential lands (cities and villages) and water resources (rivers and wetlands), and a limited extent forest lands and industries in the plain. The main water consumption in this plain is related to agricultural lands, especially paddy lands. In the study plain, due to the significant area of ​​agricultural lands and the uncontrolled development of tourism and population growth, we have faced an increase in water demand and groundwater withdrawal. In the last decade, for these reasons, groundwater use has increased significantly. As a result, we have witnessed a further drop in the water table level in the plain (Gholami et al. 2015a). The study plain is important in terms of diversity of land uses, natural recharge problems in groundwater, fluctuations in groundwater depth, and especially the significant increase in the human population.

Fig. 1
figure 1

Location of the study area (a) and the studied wells (b)

Full size image

Estimation of annual groundwater drawdown

In the study plain, there are 250 piezometric wells for groundwater studies, which are drilled for performing quantitative and qualitative monitoring of groundwater by the Mazandaran Regional Water Company (MRWC) (Fig. 1). The ​​ groundwater depth fluctuations in the mentioned wells in a 5-year statistical period (2016 to 2020) were investigated. The rates of annual groundwater drawdown were estimated based on the difference between the maximum groundwater level (beginning of spring) and the minimum groundwater level (beginning of autumn) in meters. The highest level of groundwater in early spring is observed due to precipitation in the cold seasons and lack of agricultural activities during the cold seasons. Moreover, the lowest groundwater level is observed at the end of summer and before the onset of autumn rains. In fact, during the warm seasons of the year, agricultural activities and withdrawal of groundwater lead to groundwater depth drawdown and record the lowest groundwater depth in late summer or early autumn. The 5 years studied were almost normal in terms of climate and precipitation and we did not have a serious drought period. The drawdown values ​​in the study wells during the 5 years in question have changed due to changes in precipitation, changes in the use of agricultural lands, and the development of residential areas. Finally, the mean annual drawdown of the groundwater depth in the studied 5-year period was determined as the mean groundwater depth for all of the studied wells.

Model inputs in predicting groundwater depth drawdown

Fluctuations in groundwater depth are influenced by factors including withdrawal values, water table level, topography (slope and elevation), the transmissivity of the aquifer, spatial location in the watershed, distance from water sources, annual evaporation, annual precipitation, and distance from residential centers and industries. Groundwater depth has an important effect on the amount of withdrawal and water table drawdown (Adamowski and Chan 2011). Groundwater depth was determined based on observational data (the groundwater depth in the study wells). Then, using the mean groundwater depth and also the interpolation capabilities (GIS), the raster map of the mean groundwater depth in the plain was estimated. Transmissivity of aquifer formations is one of the important hydrodynamic parameters in good discharge, the amount of withdrawal, and recovery of a well. Therefore, this parameter will be effective in dropping the groundwater (Gholami et al. 2015a, b). Based on the data of MRWC and pumping tests in study wells, the transmissivity at the location of the wells has been determined. Then, the map of the mean transmissivity of aquifer formations was prepared based on the transmissivity values and the map of the homogeneous transmissivity areas (MRWC).

Groundwater withdrawal rates are one of the most important determinants in the amount of groundwater drawdown (Shi et al. 2016). Determining the amount of groundwater withdrawal and access to accurate data is difficult, especially in the case of agricultural wells in Iran because these wells do not have smart meters. Therefore, the data of withdrawal volumes in all drinking water wells (rural and urban), as well as industrial wells, were obtained from the Mazandaran Water and Sewerage Company (MWSC) and their annual withdrawal values ​​were determined. On the other hand, a precise agricultural cadastre map was produced in the plain area in which all land uses, especially paddy lands and gardens, were identified. Finally, the maximum influence radius of the studied wells was considered to be 1 km (Shi et al. 2016). The withdrawal values ​​of drinking water wells and the withdrawal values ​​of industries wells were estimated in the influence radius of the wells. Further, withdrawal values of the agricultural lands were estimated based on land use areas and apply water requirements to each cultivation pattern.

The withdrawal values ​​of one hectare of paddy field were about 11 thousand cubic meters and one hectare of the garden was about 6 thousand cubic meters per year in the plain (MRWC). Finally, the sum of drinking, industrial and agricultural withdrawals was considered as annual withdrawal within the influence radius of the well. Raster layers of agricultural lands and the location of drinking water wells and industries as well as the GIS capabilities were used and the annual withdrawal values were evaluated. The total areas of ​​paddy fields, gardens, and withdrawal volumes of the wells (in the influence radius of the well) were estimated and added in raster format for each location of the plain.

Climatic factors (precipitation and evaporation) are effective in recharging the groundwater and also water table drawdown (Guevara-Ochoa et al. 2018). To estimate the spatial distribution of precipitation and evaporation in the plain, statistics of annual precipitation (climatology stations) and annual evaporation (evaporation stations) for 30 years in the GIS environment were used. In this regard, we have used the interpolation technique in the GIS environment and the maps or raster layers of annual average precipitation and evaporation were prepared.

Topography (slope) has an important effect on the hydrological conditions of an aquifer (Abd-Elhamid et al. 2020). To study topographic changes in the study plain, we used a digital elevation model (DEM) with a resolution of 10 m. Moreover

, the distance from water sources is one of the effective factors in compensating for the drawdown of the water table during the withdrawal (Awasthi et al. 2005). Rivers, wetlands, and lakes of the study plain were surveyed based on topographic maps and satellite images and the distance map of water sources in the GIS environment on the plain was prepared.

Industrial centers are centers for drilling wells and groundwater withdrawal. Their indiscriminate activities and withdrawal can lead to dropping water tables (Gholami et al. 2015a). Satellite images were used to prepare a database of the plain's industries. Residential areas were also surveyed based on satellite images. Then, distance maps of industries and residential areas were prepared in the GIS environment.

Modeling of groundwater drawdown by using the CANFIS network and GIS

The CANFIS is a kind of adaptive neuro-fuzzy inference system.

The CANFIS network combines a modular neural network (MNN) and adaptive fuzzy inputs to increase the accuracy of modeling process. In fact, the CANFIS integrates ANN with fuzzy inference systems (FIS) to increase network performance. The CANFIS has been used to model many hydrological parameters and has shown high performance (Vernieuwe et al. 2005; Zhang et al. 2009). The high efficiency of this network is due to the pattern-dependent weights between the fuzzy connection layer and the output layer. The CANFIS network structure is shown in Fig. 2. The CANFIS network uses a fuzzy neuron that applies membership functions (MF) to inputs. Bell and Gaussian MFs are the two main used MFs in the CANFIS network (Tabari et al. 2012). The CANFIS network uses a normalization axon to present the output in the range zero to one. The membership functions of fuzzy axons are modified through back propagation during the training stage to accelerate convergence. Further, fuzzy synapses are effective in describing the inputs that are not easily recognizable. The modular network of the CANFIS uses input rules to inputs. The number of modular networks will be equal to the number of outputs. Moreover, the number of processing elements (PEs) of each network and the number of MFs are similar. Further, the

Fig. 2
figure 2

A view of the CANFIS structure

Full size image

CANFIS network uses a hybrid axon for processing MF outputs in MNN outputs (Tabari et al. 2012). Finally, the outputs are guided by a final output and the error is back-propagated to the MFs and the MNNs. The layer functions are as follows: the nodes in the 1st-degree layer are a member of a fuzzy set and they determine the value of input given to the fuzzy sets. The second layer receives the multiplied input by all outputs from the first layer. The upper component of the third layer uses the MFs to the inputs and the upper component of the third layer is a representation of the MNN that estimates the sum of the firing strengths for the outputs. Final layer or t

he fourth layer will normalize the output weight of the components from the previous layer and presents the final output. Generally, two fuzzy models are used in the use of neuro-fuzzy inference systems, which include

Tsukamoto model and Sugeno model (Aytek 2009).

NeuroSolutions software was also used for the modeling process by using CANFIS network. In the modeling process, groundwater drawdown values ​​were considered as output and all effective factors were considered as inputs of the CANFIS network. First, all data were normalized and then randomized. In the next step, the data were divided into three categories: training data (65% of data), cross-validation data (10% of data), and test or validation data (25% of data). Further, correlation analysis between inputs and output was performed to evaluate the network inputs and determine the main factors of groundwater drawdown.

To determine the optimal inputs in the modeling process, different structures of inputs were used using a trial–error approach and evaluation of the network performance (Gholami et al. 2015b). The purpose of the network training was to achieve the network that has the highest efficiency and minimum error in the groundwater drawdown modeling. Evaluation criteria of the network performance were the correlation between the simulated values ​​and the observed values ​​as well as statistical error indices such as mean squared error (MSE) and coefficient of determination (R-sqr). Finally, the optimal structure of the CANFIS network to simulate the rates of groundwater depth drawdown was determined by using the trial–error method, evaluating the network error in the training and testing stages. In the next step, the inputs of the tested CANFIS network were prepared as digital geo-referenced layers in the GIS.

Then, they were combined with equal pixel size and the network inputs data (groundwater depth, transmissivity of aquifer formations, withdrawal volumes) with geographic coordinates for the pixels were entered and used into the tested CANFIS network.

The process of estimating drawdown values at the location of each pixel was performed using the tested network and the output with geographic coordinates was entered with the GIS environment. Then, using the capabilities of the GIS, the results of the simulation of drawdown values were presented as a map of annual groundwater drawdown values.

Further, the observed values ​​of groundwater drawdown in the study wells were overlapped on the simulated drawdown map and the simulation accuracy and the resulting drawdown values ​​were compared and evaluated.

Results

The recorded groundwater depth fluctuations (annual drawdown) in study wells have been between 0.15 and 4.4 m per year. Moreover, the mean annual drawdown in the wells was 1.7 m in the studied 5-year period. The range of factors such as distance from water sources, distance from industrial centers and population centers varies from about zero to several kilometers. Further, the normal depth of groundwater in the study plain varies from 0.5 to 40 m. The elevation of the plain is between 0 and 40 m and the plain has a slope of less than 5 percent. There is a shallow water table on the coasts of the study area and the lowest water table is observed at the end of the plain (in the vicinity of the mountains.

). The range of normal annual precipitation and evaporation changes are between 600 to 1300 mm and 875 to 1000 mm per year, respectively.

Annual withdrawal values ​​within the influence radius (one kilometer) of wells were calculated between 0.1 and 3.6 million cubic meters per year. The mean annual withdrawal in study wells has been about 2 million cubic meters per year. The maximum withdrawal is related to wells around which there was a range of paddy lands and drinking water supply wells. A summary of the estimated data on the inputs and output of the neural fuzzy network is presented in Table 1.

Table 1 A summary of the CANFIS inputs and output for modeling the groundwater drawdown
Full size table

Correlation analysis was used to define the affecting factors in groundwater drawdown between inputs and groundwater drawdown. Correlation coefficients between annual drawdown and the affecting factors in groundwater drawdown are given in Table 2. As can be seen, factors such as transmissivity of aquifer formations, withdrawal values, and groundwater depth have the highest correlation coefficients, respectively. These factors are the most important factors in the groundwater fluctuations (Awasthi et al. 2005; Saemi and Ahmadi 2008; Gong et al. 2018).

Table 2 Correlation coefficients between the input variables and groundwater depth drawdown
Full size table

The trial–error method was used to determine the optimal inputs and the optimal fuzzy neural network structure in the modeling of the annual groundwater drawdown. The trial–error method and error evaluation in the training and test stages showed that the three mentioned factors are the best inputs for the modeling process. According to the results, the membership function of the Bell and the Takagi–Sugeno–Kang (TSK) fuzzy model are the best options for the optimal structure of the CANFIS network, which in previous studies were also considered as one of the best options (Vernieuwe et al. 2005; Zhang et al. 2009). Moreover, neural fuzzy network training has had good results in the training stage, the results of which are presented in Table 3.

Table 3 Performance evaluation of the CANFIS network in the training stage. In the cross-validation stage, MSE and standard deviation (SD) were 0.009 and 0.0007, respectively
Full size table

After network training, testing of the CANFIS network was performed and the results of the test phase are given in Table 4. According to the values ​​of indices such as R-sqr and MSE of the CANFIS network has a good performance for simulating the annual groundwater drawdown. Moreover, the comparison between the simulated values ​​and the observed values ​​of groundwater drawdown in the test stage is presented in Fig. 3. As can be seen, there is a good correlation between the simulated values ​​and the observed values. Then, the maps or raster layers of the optimal inputs of the CANFIS network (groundwater depth, the transmissivity of aquifer formation, and annual withdrawal values) were prepared in the GIS environment (Fig. 4). Finally, the mentioned layers or maps were combined in a GIS environment with equal pixel size and a geo-referenced output was prepared from the optimal network inputs to simulate the groundwater drawdown values ​​in the study plain area. Then, the mentioned inputs were used in the tested CANFIS network and the annual drawdown values ​​in all areas of the plain were estimated. The predicted values ​​in the GIS were presented as a map of the annual groundwater drawdown values. Figure 5 shows the annual groundwater drawdown values. To evaluate the accuracy of the results, the observed values of groundwater drawdown in study wells were overlapped on the map and were compared with the map. This comparison ​​indicates the high performance of the used methodology. The results showed that the CANFIS network has a good performance in the training and testing stages. Furthermore, the CANFIS network in moderate values of groundwater drawdown is more efficient than the maximum and minimum drawdown values.

Table 4 Performance evaluation of the CANFIS network in the testing stage
Full size table
Fig. 3
figure 3

Comparison between the simulated groundwater drawdown and the observed values in the test stage of the optimized CANFIS network

Full size image
Fig. 4
figure 4

Maps of effective factors in the annual groundwater drawdown. (a) The mean transmissivity of aquifer formations (m2/day), (b) the used land uses and the wells in the calculation of groundwater withdrawal values, and (c) the mean groundwater depth (m)

Full size image
Fig. 5
figure 5

Annual groundwater drawdown map (m) in the study area. The observed values of annual drawdown in the studied wells have been overlapped with the map for evaluating the accuracy of the obtained results in the modeling of the annual groundwater drawdown

Full size image

Discussion

The frequency of groundwater depth drawdown of more than two meters in the study plain is significant. It was also measured that the water table drop by seven meters in 1 year in a well at the end of the plain. The maximum rates ​​of groundwater depth fluctuations are observed in places with low groundwater table, coarse-grained formations, and high groundwater withdrawal. Moreover, in the coasts located at the outlet of watersheds, the accumulation of surface water in those places and higher precipitation (Caspian Sea effect), the groundwater drawdown is less. Therefore, the groundwater depth is higher and their monthly fluctuations are less (Shiri et al. 2013).

Among the studied factors, groundwater depth, withdrawal values, the transmissivity of aquifer formations, annual precipitation, site elevation, distance from industries and residential centers have a significant relationship with groundwater depth fluctuations. The factors of the transmissivity of the aquifer, withdrawal values, ​​and groundwater depth have the highest correlation coefficients with groundwater drawdown. The correlation coefficients between them are 0.8, 0.69, and 0.6, respectively. The higher transmissivity leads to a larger influence radius for the well and is exploited while pumping higher discharges from a farther field. Therefore, according to the results, the amount of groundwater withdrawal is also directly related to the groundwater drawdown (Awasthi et al. 2005; Saemi and Ahmadi, 2008; Gong et al. 2018).

Precipitation is one of the main factors affecting groundwater depth fluctuations. According to the results, there is an inverse relationship between precipitation and groundwater drawdown values ​​(Shiri et al. 2013). However, this relationship is not very strong in the study plain, and in groundwater drawdown values ​​are not effective. Place elevation is an effective factor in the depth of the groundwater in alluvial or unconfined aquifers. Low lands have more water intake capacity and groundwater depth is generally higher in them and as a result, they will have lower drawdown values. The elevation of the place in the plain will to some extent indicate the location of the watershed.

Evaporation has a significant and weak relationship with the amount of groundwater drawdown in the plain. Because evaporation by reducing surface water resources will ultimately affect the amount of groundwater recharge (Sahour et al. 2020). Distance from water resources can play an important role in groundwater depth fluctuations. Groundwater drawdown in lands adjacent to rivers can be compensated by the river. However, based on the analysis of statistics and available data, there was no significant relationship between this parameter and the groundwater drawdown values ​​in the study plain. Distance from industries and residential centers also have a significant relationship with the annual drawdown, but these relationships are not very effective. These places are the place to dig wells and exploit groundwater.

The results of the simulation of groundwater drawdown values ​​using the CANFIS network showed that the network has acceptable performance. Evaluating the results of the training stage through error indices and comparing the observed and simulated values ​​indicates a high performance of the CANFIS network in simulating the groundwater drawdown. What is certain is that a tested model generally simulates normal values ​​with higher accuracy and will have more errors at the minimum and maximum values (Sahour et al. 2020). In groundwater drawdown studies, accurate prediction of maximum groundwater drawdown values ​​is important and can be important data in water resources management planning. Based on the results, the CANFIS network has a high ability to estimate the maximum groundwater drawdown values. Finally, the tested CANFIS network was used to simulate the groundwater drawdown values ​​in the plain. The distinctive feature of this modeling is that only by using three main inputs effective in groundwater drawdown and an optimal neural fuzzy network, groundwater drawdown values ​​can be estimated in any place. Moreover, providing a map of groundwater drawdown values ​​whose accuracy has been confirmed can be an effective expression for water resource managers as well as a way to share the results of current CANFIS modeling for everyone.

The important point about the methodology of the present study is that the three main inputs, namely groundwater depth, the transmissivity of aquifer formations, and withdrawal values ​​are needed to predict the drawdown values, all of which are easily accessible or calculable. Further, groundwater depth and groundwater withdrawal values ​​vary over time. These conditions make it possible to use the present methodology for the temporal changes of groundwater drawdown or to study the effect of different scenarios of groundwater withdrawal by the model. The important result of the present study is the possibility of predicting the annual groundwater drawdown in any place in a short time and with high accuracy and the possibility of presenting the results in the form of a map or the geo-referenced digital layers.

Conclusion

Predicting groundwater depth drawdown ​​is necessary and practical in water resources management. On the other hand, field measurement will be costly and time-consuming, and modeling-based estimation is difficult and complex because it is difficult to estimate important inputs such as withdrawal values. Therefore, the use of artificial intelligence and the selection of appropriate inputs can be an effective tool for estimating the amount of groundwater drawdown. The first step in the modeling process is to determine the main inputs and accurately estimate them, and then to use an efficient modeling method correctly. In this regard, the fuzzy neural network can be a good choice to simulate groundwater drawdown values or groundwater depth fluctuations.

Different fuzzy neural network structures, as well as models with different inputs, can be used for modeling. For example, if the water table parameter is not available, a model with a lower accuracy can be used without considering this parameter. Distinctive features of the neural fuzzy network in simulating groundwater fluctuations are the high performance, low cost, high modeling speed, the ability to couple to other systems such as GIS. Moreover, the possibility of using different structures and models with inputs appropriate to the conditions of the region is one of its strengths. The CANFIS network can be used to simulate changes in groundwater drawdown in other plains in the discussion of spatial changes and even temporal changes in groundwater drawdown. Because, by determining the different amounts of groundwater withdrawal at different times, the neural fuzzy network can be used to estimate the drawdown values ​​with other appropriate inputs. Further, the combination of neural fuzzy network and GIS can be used as a method to estimate groundwater drawdown in any place and time. For future studies, it is suggested to use other methods of artificial intelligence such as learning machines in the modeling of groundwater depth drawdown.