Introduction

The ever-increasing world population has placed an excessive demand on water resources (Bouwer 2000), and it has become necessary to prevent the pollution of freshwater resources. Due to this increasing population, huge volumes of sewage wastewater are produced which need to be treated before being released back into the environment.

Sewage wastewater is characterized by the presence of organic matters, pathogens, suspended solids, and nutrients such as phosphorus and nitrogen in its water bodies (Dawood and Li 2013). These nutrients have adverse effects on the water reservoirs as they cause eutrophication, a condition which deteriorates water quality (Renuka et al. 2015). Strict water regulations have been introduced to limit the amount of nutrients present in effluent streams flowing into water resources to prevent the nutrients from polluting them. Recently, Yaser and Safie (2020) suggested several methods for sewage processing for water recycling, e.g., biological treatment, membrane technology and adsorption.

The coagulation-flocculation process is one of the most efficient and simple chemical treatment processes for wastewater (Devi and Dahiya 2008). The mechanism of the process mainly involves aggregation of suspended solid particles into settleable flocs by charge neutralization of colloids, neutralizing the negative charges which had kept the particles apart (Li et al. 2016). Organic polymers, iron and aluminum salts are mostly used to neutralize the colloids to form larger flocs which can be separated from the liquid phase by sedimentation or filtration. The efficiency of the process depends on several factors which include the type, dosage, and basicity of the coagulant (Hu et al. 2006, Nandy et al. 2003, Teh et al. 2014, Wang et al. 2002), pH in the solution (Elmaleh et al. 1996, Miller et al. 2008, Syu et al. 2003), mixing speed and time (Kan et al. 2002, Khan et al. 2014, Li et al. 2016, Yu et al. 2011).

The coagulation-flocculation process is a well-researched process which has been utilized for years. However, it has a unique solution for every type of wastewater treated since the characteristics of wastewater varies from point to point and is the determinant for the type of chemical reagents to be used for the process.

This study focuses on the development of a water treatment program for sewage wastewater and the optimization of the coagulant and flocculant dosages to increase efficiency. Response surface methodology (RSM) was utilized to develop the experiment, minimize the number of experiments, determine the relationship between multi-variables and optimize the program based on the multi-variables responses, percentage removal of turbidity and total dissolved solids (TDS) from the water. Response surface methodology (RSM) is an efficient models-building mathematical statistics method used to evaluate the effects of multiple variables and determine the optimal conditions to give desirable responses (Bezerra et al. 2008, Witek-Krowiak et al. 2014).

Experimental

Sample collection

The sewage wastewater samples were collected from a sewer network at Matla Power Station in South Africa. The water samples were characterized by the following parameters in both the pre- and post-treatment: pH, turbidity and dissolved solids. Table 1 summarizes the characteristics of the sewage wastewater sample used for the study.

Table 1 Characteristics of wastewater sample
Full size table

Chemical reagents

Seven different types of coagulants were obtained from NCP CHLORCHEM Pty (Kempton Park, South Africa). The utilized coagulants, U3500 and U3750 are part of the U3000 series of aluminum chlorohydrate coagulants manufactured by the company. The other coagulants, U6000, U6050 and U6750 used for the experiment are part of the U6000 series of cationic polymer chlorohydrate coagulants. Ferric chloride and aluminum sulfate (Alum) are the other coagulants which were used. Floc858 and Floc887 are the chemical reagents which were utilized to aid flocculation after coagulation. All the coagulants were supplied in liquid form while the flocculants were supplied in powder form.

Reagent stock solutions

The different coagulant stock solutions were prepared by mixing 1 mL of each coagulant in 1000 mL of distilled water to form 1000 ppm stock solutions. The stock solutions of the flocculants were prepared by dissolving 1 g of each flocculant in 1000 mL of distilled water to also produce 1000 ppm solutions.

Selection of the most efficient reagents

Before carrying out the study, we had to first determine the most efficient coagulant and then determine the flocculant that is the most efficient when combined with it from the available chemicals. This was achieved by conducting the jar test of all the coagulants.

A wastewater sample of 250 ml in a beaker was dosed as required, stirred rapidly with a spatula for 30 s and then left to rest for 10 min before taking measurements of the turbidity and TDS. The experiment was repeated for 10 mL (40 ppm), 20 mL (80 ppm) and 30 mL (120 ppm) dosages for each coagulant. After determining the most efficient coagulant, jar tests of a combination of the efficient coagulant and available flocculants were conducted. The same series of steps were followed for the coagulation stage using 200 mL sample of wastewater. After 10 min of settling time following the coagulant dosing, a dose of flocculant was introduced, and the solution was stirred gently for 1 min. The solution was then allowed to rest for 40 min before measurements were taken. This was repeated for 5 mL (25 ppm), 10 mL (50 ppm), 15 mL (75 ppm), 20 mL (100 ppm) and 25 mL (125 ppm).

Treatment process

After determining the most efficient coagulant-flocculant combination, experiments for achieving the objectives of this study were carried out by using the jar test at various dosages of the selected reagents using 120 mL of the sample water. The percentage turbidity and TDS removal were used to measure the efficiency of the chemicals at different dosages. The percentage removal efficiencies of turbidity and TDS were calculated by the following formula:

$${\text{\% Removal efficiency}} = { }\left( {\frac{{{\text{x}}_{{\text{i}}} - {\text{x}}_{{\text{f}}} }}{{{\text{x}}_{{\text{i}}} }}} \right) \times 100$$
(1)

where xi and xf are the initial and final measurements, respectively, for either turbidity or TDS before and after treatment.

Experimental design

The experiment was designed using the RSM to reduce the number of experiments conducted and to optimize the developed program by finding the optimal dosages which will maximize the removal efficiencies (Bezerra et al. 2008). Several experimental designs are available in RSM which include the Box–Behnken design and Doehlert design but for this study, RSM used the Central Composite Face Design (CCFD) which calculates the number of experiments by the following equation:

$${\text{Total number of experiments }} = \, 2^{k} + \, 2k \, + \, 2$$
(2)

where k is the number of independent variables.

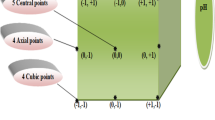
Coagulant and flocculant dosage were the independent variables in the study; hence, the total number of experiments was 10. The RSM design was developed by utilizing Design-Expert software. The software requires three levels, the minimum (− 1), the median (0) and the maximum (+ 1) for the independent variables (coagulant and flocculant dosage) and their real values as shown in Table 2. The maximum dosage was stated in the research question while the minimum was determined (Fig. 1).

Table 2 Real values of the coded levels
Full size table
Fig. 1
figure 1

Matla Power Station (S26.28036 E29.14229)

Full size image

Results and discussion

Selected reagents

The results of the preliminary experiments for determining the most efficient coagulant from the available seven are shown in Fig. 2. The least efficient coagulant was determined to be U6000 with a maximum turbidity efficiency of 25% making it the least favorable coagulant for the treatment of sewage wastewater. The U6750 coagulant demonstrated to be the most efficient coagulant with a maximum turbidity removal of 90%. This implies that the chemical was more efficient in the destabilization of colloidal particle hence the high turbidity efficiency. The turbidity removal increases with increase in dosage, but this is not always the case as overdosing can result in poor flocculation (Aghapour et al. 2016).

Fig. 2
figure 2

Preliminary coagulation

Full size image

The U6750 coagulant demonstrated very high efficiency in the removal of turbidity when combined with either of the available flocculants. However, it was most efficient when combined with Floc887 resulting in a maximum turbidity removal of 94% at 125 ppm (25 mL), as shown in Fig. 3. The flocculant was added to aid flocculation after a coagulant dosage of 120 ppm had been added to the water. After flocculant dosing, turbidity removal efficiency of the experiment increased by 4%. The chemicals which were to be used for the rest of the study were U6750 and Floc887.

Fig. 3
figure 3

Turbidity removal efficiencies of flocculants in combination with U6750

Full size image

Statistical analyses

Table 3 shows the experimental design that was used, and the results obtained when carrying out the jar test for various dosages of the coagulant and dosage. The real values for the code levels used can be found in Table 2.

Table 3 Experimental design and results for the jar test using U6750 and Floc887
Full size table

Determining the relationship between the coagulation-flocculation is important in understanding how the dosages affect the response factors, turbidity and TDS levels. RSM was utilized to conduct this analysis and various models are available for correlation with the experimental data. Some of the few models available are mean, linear, quadratic, cubic and quartic model. The selection of the most significant model is based on its ability to correlate with the experimental data. It is important to conduct an analysis of variance before selecting a model by comparing their standard deviation and R2 value. The model with an R2 value as close as possible to a value of 1 and smallest standard deviated is considered the most significant model (Ghafari et al. 2009). Other parameters assessed to determine the significance of a model are the F value and P value (probability value).

Analysis models

The quadratic and linear models were determined to be the most significant models to correlate turbidity and TDS removal responses, respectively, with experimental data. The R2 values obtained were 0.99 and 0.94 for turbidity and TDS removal, respectively. This implies that 99% and 98% of the variations in the response factors, turbidity and TDS removal, respectively, can be explained by the independent variables, coagulant and flocculant dosage. The developed models for both responses have a ‘Prob > F’ value less than 0.050 as shown in Table 4. Their standard deviations are 1.31 and 1.42 for TDS and turbidity removal, respectively, which are relatively small, indicating the significance of the selected models (Trinh and Kang 2011).

Table 4 Analysis of variance (ANOVA) results
Full size table

The final response equations of both responses are shown below (Eq. 3.1. and Eq. 3.2). The equations are expressed in terms of the actual factors and they describe the relationship between the response (turbidity or TDS removal) and the independent variables (coagulant and flocculant dosage).

$${\text{TDS}}\,\,{\text{Removal }} = \, 3.05 \, + \, 0.073A \, + \, 0.090B$$
(3)
$${\text{Turbidity}}\,{\text{Removal }} = \, 50.9 + \, 0.737A \, + \, 0.064B \, - \, 6.00 \times 10^{ - 4} AB \, - \, 3.06 \times 10^{ - 3} A^{2} - \, 5.71 \times 10^{ - 5} B^{2}$$
(4)

Diagnostic plots were also used to assess the suitability of the selected model. The diagnostic plot used is a plot of actual experimental values versus the predicted values obtained from the developed response equations. From Fig. 3a and b, the actual values and predicted values agree for both responses.

Treatment process analysis

The response surface plots for turbidity and TDS removal are shown in Fig. 3a and b, respectively. The turbidity removal surface plot showed that overdosage of the coagulant and flocculant would eventually result in a decrease in efficiency of turbidity removal and that a peak existed in the current design space. The experimental range would result in optimal conditions which would maximize turbidity removal response and maximum turbidity removal would be achieved at dosage levels above 120 ppm for the coagulant and flocculant.

In Fig. 3b, the response surface of TDS removal showed that the optimal solution for TDS removal existed in the experimental range. However, it would be achieved when both the coagulant and flocculant are close to the maximum dosages.

Treatment process optimization

When optimizing a multivariable process, it is important to determine optimal condition in which all parameters simultaneously result in the maximum removal of all response variables (Sincero and Sincero 2002). The optimum condition was determined by setting up a desirable function which would maximize the removal of both turbidity and TDS within the dosage range (25–125 ppm). The minimum constraints used for the desirability function were chosen to be close to the obtained maximum removals efficiencies from the experiments for both response variables to obtain a precise prediction of the optimal solution. Table 5 summarizes the constraints which were used to set up the desirability function.

Table 5 Desirability function constraints
Full size table

The desirability function in Design-expert produced an optimal removal efficiency of 93.3% for turbidity and 23.2% for TDS. The optimal removal efficiencies were obtained at a coagulant dosage 120.9 ppm and flocculant dosage 125 ppm. An additional experiment was conducted applying the optimum conditions for verification of the developed models. The obtained results, shown in Table 6, indicate that the developed models are accurate and reliable as the removal efficiencies obtained from the confirmatory experiment are in close agreement with model response results from the developed response equations (Fig. 4).

Table 6 Optimum conditions confirmatory results
Full size table
Fig. 4
figure 4

Actual vs Predicted plots for a Turbidity removal; b TDS removal

Full size image

Zahrim & Dexter (2016) investigated the removal of the color in a palm oil mill biogas plant wastewater (POMBPW) effluent using the coagulation/flocculation process and polyDADMAC as a sole coagulant. It is the same process used in this study. The differences between the two studies are in the parameters investigated. Zahrim & Dexter’s sample was a POMBPW effluent and they investigated its color removal and conductivity, but these researchers’ sample was a power station wastewater effluent and they investigated turbidity and TDS. While Zahrim & Dexter found Ferric Chloride ineffective in removing coloration from the POMBPW, these researchers found it to be moderately effective (63%) in reducing the turbidity of the wastewater. Furthermore, polyDADMAC (1000 ppm) obtained a coloration removal efficiency of 40–56% Obidike and Madigoe, using polyDADMAC (U6750) (120.9 ppm) reduced turbidity by 90% and when the flocculant, Floc887 (125 ppm), it increased to 93.3% (Fig. 5).

Fig. 5
figure 5

Response surface plot for a Turbidity; b TDS removal

Full size image

Cost/Efficiency analysis of the coagulants

The costs of the different coagulants are wide apart, and a cost/efficiency plot becomes necessary especially when it was discovered that the most efficient coagulant, U6750 (90%) is also the most expensive coagulant. Figure 6 is the resultant plot showing the two points of intersection which are possible feasible coagulants to choose from.

Fig. 6
figure 6

A Cost/Efficiency plot of the coagulants

Full size image

Point A conforms to about 48% Turbidity Reduction Efficiency (TRE) and fell between the relatively cheaper U3750 and U6000 at about R8 800. Hence, a blend of the two coagulants would be investigated to achieve the 48% TRE if that will be the point of choice. However, point B gives a higher TRE of 90% but double the cost of point A, at about R16 000. Considering that health of humans, plants and animals are in consideration here, U6750 corresponding to point B should be the feasible coagulant even though it is costlier than that at point A because a 90% TRE is much higher than a 48% TRE.

Conclusions

The coagulation-flocculation process is one of the most reliable physical–chemical methods which are used for water treatment. In this study, a water treatment program was developed for the treatment of sewage wastewater by initially identifying the most efficient chemicals through a laboratory jar test. A multiple response optimized method was used to evaluate the influence of the important operating variables (coagulant and flocculant dosage) and the process successfully optimized. The study showed that the coagulant U6750 is the most efficient chemical in removing the pollutants (TDS and turbidity) when combined with the flocculant Floc887. The optimal conditions obtained were with dosages of 120.9 ppm of U6750 and 125 ppm of Floc887. This resulted in optimal removal efficiencies of 93.3% and 23.2% for turbidity and TDS, respectively, emphasizing that the combination of U6750 and Floc887 is efficient in improving the physical characteristics of sewage wastewater. The aim of the study was achieved as the developed program improved the water quality.