Introduction

The need for successful groundwater exploration planning and management for local and regional groundwater productivity mapping in the field of groundwater hydrology cannot be underestimated The importance of groundwater as a supply for a country’s socioeconomic growth is enormous, as it remains the most solved water sources in many areas due to underdevelopment of surface water. Recent population growth has imposed significant stress on the existing inadequate water scheme based solely on individual exploration exercises due to the increasing demand for water supply. Consequently, it became very expedient to expand the existing water scheme by carrying out detailed subsurface characterization, thereby leading to mapping out zones of high groundwater potentials.

Groundwater occurrence in any rock presupposes the satisfaction of two factors: adequate porosity and permeability. Sedimentary rocks exhibit these properties due to their mode of occurrence and emplacement. Sedimentary deposits maintain primary porosity that determines their storage and permeability to a great extent (Ashraf et al. 2018) which tends to make them exhibit good aquifer potential as compared to basement complex aquifers. The crystalline nature of the basement complex’s metamorphic and igneous rocks satisfies none of these requirements. Basement complex rocks are therefore considered poor aquifers due to their low primary porosity and permeability, necessary for the accumulation of groundwater (Davies and De West 1966). Olorunfemi and Fasuyi (1993) emphasized the complexity of groundwater occurrence in a basement complex terrain which can be attributed to the occurrence of primary porosity in the underlying rock. The occurrence of groundwater in a basement complex terrain can be attributed to the degree of weathering and fracturing as well as the materials that make up the saprolite zone. The complex interrelationship between geology, post-emplacement, tectonic history, weathering process, aquifer types and groundwater flow pattern therefore plays an important role in groundwater potential in a basement complex (Olorunfemi 2007). The occurrence and distribution of groundwater in crystalline units are influenced by a variety of factors including the existence and development of integrated fracture system, fracturing intensity, nature and type of fillings in the joint aperture, depth, extent, weathering pattern and thickness. Taking into account the limited and winding characteristics of groundwater reservoirs in the basement complex, the optimum potential of the aquifer network can only be extracted through a well-coordinated hydro-geophysical and geological investigation. Geo-electrical techniques are powerful tools and play a vital role in groundwater investigations particularly in delineating the aquifer structure in complex geological environments. By combining data on hydrogeological surface characteristics with information obtained from geo-electrical investigations, the subsurface characteristics and details of aquifer morphology can thus be described. The hydrogeological significance of each geo-electric parameter used to model groundwater potential will then be a function of its contribution to the occurrence of groundwater. In other words, theoretical modeling of groundwater is a spatial analysis problem involving a broad range of multiple evaluation criteria.

Several experts frequently evaluate those criteria. Rao and Briz-Kishore (1991), Adiat et al. (2013) and Mogaji and Omobude (2017) assessed the value of aquifer resistivity and thickness for future groundwater evaluation. In order to produce a high-precision groundwater distribution map, the effects of all the important geo-electrical parameters have to be integrated (Adiat et al. 2013). The use of the multi-criteria decision analysis (MCDA) in the field of hydrogeology is comparatively new (Mogaji and Omobude 2017). The advantage of the approach is its ability to carry out a systemic analysis and to combine specific criteria/factors to model the target. The most commonly used MCDA method is the analytical hierarchic process (AHP) approach (Adiat et al. 2013; Jha et al. 2010; Mogaji and Lim 2016; Mogaji and Omobude 2017). Many factors such as lithology, drainage pattern, lineament density and geo-electric parameters (thickness, resistivity, transverse resistance, coefficient of anisotropy) are believed to be influencing groundwater potential (Adiat et al. 2013; Mogaji and Lim 2016; Akinlalu et al. 2017). The invention of geographic information system (GIS) has made possible spatial distribution mapping and integration of different data sets. Its applicability in the field of hydrogeology has been widely explored (Nampak et al. 2014; Singh et al. 2014; Mogaji and Lim 2016; Mogaji and Omobude 2017). Their work has shown the effectiveness of GIS to carry out MCDA prediction models in environmental decision-making processes.

Though groundwater has in previous years been explored in the study area through the drilling of boreholes, however, some of these boreholes are characterized by low and intermediate yield. In order to reduce the level of risk associated with borehole drilling, it is important to have background knowledge about the groundwater potential distribution within the area and this can be done by carrying out a detailed study of the aquifer system and spatial distribution mapping of groundwater potential markers within the region. This study thus tends to develop MCDA-based groundwater potential model by integrating geophysical and GIS techniques.

Location and geology of the study area

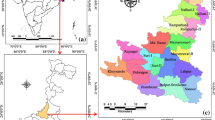
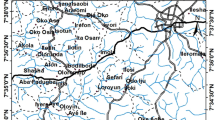
The area investigated which encompasses Lokoja, and its environs is located between Latitudes 7°45′00″ and 7°51′00″ and Longitudes 6°38′30″ to 6°44′00″ at the north-central part of Nigeria with a total surface area of 123 km2 (Fig. 1). The geological setting of the study area consists of the occurrence of both basement complex and sedimentary rocks (Fig. 2). The western flank is covered by crystalline basement complex of Precambrian age, consisting of migmatite and migmatite gneiss, undifferentiated granite and granite gneiss and biotite hornblende gneiss. The eastern flank is covered by Cretaceous to Recent sediments of the southern Bida Basin such as alluvium and feldspathic sandstone and siltstone. The area falls within the Guinea Savannah climate belt of West Africa which is characterized by two distinct seasons, the wet and dry seasons. The average rainfall of Lokoja was found to be 1213.877 mm (Olatunde and Isaac 2018). The average annual temperature rarely falls below 30.7 °C, with February and March being the hottest months (Olatunde and Ukoje 2016).

Fig. 1
figure 1

Topographical map of the study area

Full size image
Fig. 2
figure 2

Geological map of the study area (Ojoina 2014)

Full size image

Methodology

In order to carry out detailed subsurface characterization, both geophysical and hydrogeological investigation was employed. A total of one hundred and twenty-four (124) vertical electrical sounding (VES) (Fig. 3) data with a distribution density of 1.01 VES per unit km2 were collected within the study area using the Schlumberger configuration of electrical resistivity survey with maximum AB/2 spacing of 100 m. The obtained data were plotted on a log–log graph. Master curves (Orellana and Mooney 1966) and auxiliary point charts (Zohdy 1965; Keller and Frischknecht, 1966) were used to manually classify the field curves. The layered parameter obtained from the manual interpretation was then used as an input model for the computer-aided iteration of the WINRESIST interpreting system (Vander Velpen 1988). The sounding curves were interpreted to determine the true resistivity and thickness of the subsurface which was further interpreted to obtain the Dar-Zarrouk parameters. Hydrogeological investigation of one hundred and twenty-four (124) randomly selected boreholes drilled within the study area was undertaken to obtain in situ information on the subsurface (Fig. 3). Parameters such as elevation, static water level, borehole depth and borehole yield were obtained to determine the groundwater flow direction within the study area.

Fig. 3
figure 3

Topological map showing the VES and borehole points

Full size image

A Multi-Criteria Evaluation Analytic Hierarchy Process (MCE-AHP) approach developed by Saaty (1980) was employed to model groundwater potential. The influencing factor used for the prediction (aquifer thickness, aquifer resistivity, coefficient of anisotropy and transverse resistance) was classified and rated as shown in Table 1. A knowledge-based AHP classification was employed. Studies by Adiat et al. (2012), Adiat et al. (2013) and Mogaji and Lim (2016) have identified the hydrogeological importance of these influencing factors. Thematic maps for each predictor were generated having being assigned rates and weight on the numerical scale depending on the influence rate of each parameter on groundwater occurrence. A ranking scale of 1 to 3 was used with 1 being the lowest, 2 being the average and 3 being the highest. Groundwater potential index (GWPI) was estimated by applying the weighted linear combination as expressed in Eqs. 1 and 2.

Table 1 Probability rating (R) for classes of the parameters (modified after Mogaji and Omobude 2017)
Full size table

Mathematically, according to Adiat et al. (2012), groundwater yield index for each VES point can be defined as:

$${\text{GW}}YI = W_{i} R_{i}$$
(1)

where Wi is the weight (w) of parameter I and Ri is the rating score (R) of parameter i.

Therefore, GW = f(CA, AT, BY, AT) where GW is groundwater, CA is coefficient of anisotropy, AT is aquifer thickness, BY is borehole yield and AT is aquifer thickness.

According to Adiat et al. (2012), the groundwater potential index value is given by the equation:

$${\text{GW}}PI = {\text{CA}}_{w} {\text{CA}}_{R} + {\text{AT}}_{W} {\text{AT}}_{R} + {\text{BY}}_{W} {\text{BY}}_{R} + {\text{AT}}_{W} {\text{AT}}_{R}$$
(2)

The obtained groundwater potential index value obtained at each VES point was imported into an ArcGIS environment. Inverse distance weighting (IDW) geostatistical tool was employed to generate the groundwater potential map. Figure 4 shows a simplified flowchart of the methods used in this research.

Fig. 4
figure 4

Flowchart showing the methods used for the study

Full size image

Results and discussion

Geophysical interpretation

The layered parameter (resistivity and thickness) obtained from 1D electrical resistivity inversion was interpreted to obtain aquifer resistivity, aquifer thickness, coefficient of anisotropy. The longitudinal resistivity was interpreted to be the aquifer resistivity for areas underlined by basement rocks, while transverse resistivity was interpreted as aquifer resistivity for sedimentary terrain. These values were used as the aquifer resistivity in the study area since it is characterized by both longitudinal and transverse flow as described by Reiter (1981).

Aquifer resistivity value varies between 11 and 250 Ωm (mean: 111 Ωm) (Table 2). Figure 5 illustrates the spatial distribution of aquifer resistivity of the study area. The central part is characterized with low resistivity ranging from 10 to 40 Ωm. The low resistivity values can be inferred to represent good aquifer potential. The western and the southern part is characterized with medium (40—100 Ωm) to high (100–300 Ωm) resistivity values with pockets of low resistivity.

Table 2 Summary of aquifer parameters obtained from geo-electrical and hydrogeological interpretation
Full size table
Fig. 5
figure 5

Map showing the spatial distribution of aquifer resistivity across the study area

Full size image

The aquifer thickness value varies between 2.1 and 55 m (mean: 12.44 m). The spatial distribution map of aquifer thickness (Fig. 6) reveals its variation across the study area. 60% of the study area exhibits moderate aquifer thickness values (10–20 m) which is distributed across the northern and western parts of the study area. 35% of the study area is characterized by low aquifer thickness values (2–10 m) and widely distributed in the southern part of the study area and as pockets within the moderate zones. 5% of the study area exhibit extremely high aquifer thickness values (> 20 m), and they occur as pocket zones across the study area. High aquifer thickness creates a large space for the accommodation of infiltration water; however, the materials that make up these zones play a key impact in what quantity of the infiltration finally replenish the aquifer.

Fig. 6
figure 6

Map showing the spatial distribution of aquifer thickness across the study area

Full size image

As the hardness and compaction of rocks increase, anisotropy also increases (Keller and Frischknecht 1966). Therefore, zones of high coefficient of anisotropy are always associated with low porosity and permeability. Areas with a coefficient of anisotropy < 1 are considered to have considerably high groundwater potential. As shown in Fig. 7, areas with sedimentary rocks have values less than 1 which confirms the availability of primary porosity in sedimentary rocks as compared to basement rocks.

Fig. 7
figure 7

Map showing the spatial distribution of coefficient of anisotropy across the study area

Full size image

Transverse resistance is a measure of the rate of water percolation and aquifer recharge, thus making it a suitable parameter in modeling groundwater potential. On an empirical basis, it can be admitted that the transmissivity of an aquifer is directly proportional to the transverse resistance (Ungemach et al. 1969). Figure 8 shows the spatial distribution of transverse resistance across the study area which is characterized by low (< 1000 Ωm2) to medium (1000–2500 Ωm2 transverse resistance values with isolated zones of high value. According to the groundwater flow map of the study area (Fig. 9) from the estimated hydraulic head shows that the most dominant groundwater flow is from the west through the central region to the eastern part of the study area. Localized flow direction from the northern to eastern region also exists.

Fig. 8
figure 8

Map showing the spatial distribution of transverse resistance across the study area

Full size image
Fig. 9
figure 9

Map showing the groundwater flow direction across the study area

Full size image

Modeling of groundwater potential based on MCA modeling approach

The estimated groundwater potential index values were used to generate the spatial distribution of groundwater potential of the study area by adopting the quantile classification technique used in the studies of Mogaji and Omobude (2017) in which sets of values were distributed into classes of an equal number of values. The region groundwater potentiality prediction index (GPPI) maps were generated in a GIS setting using the classification ranges in column 2 of Table 3. The generated groundwater potential yield index map (Fig. 10) classifies the potential rate into three classes (low, medium and high) using a spatial attribute band of < 1.4, 1.4–2.6, and > 2.6 (Table 3). The corresponding percentage area covered in each groundwater potential zone is described in Table 3. From the result obtained, 66% of the study area can be described to exhibit medium rate groundwater potential with low and high zones having an area coverage of 22% and 10%, respectively.

Table 3 Characteristics of the groundwater potential map based on the applied MCDA—AHP model (Mogaji and Omobude (2017)
Full size table
Fig. 10
figure 10

Spatial distribution of groundwater yield index across the study area

Full size image

Validation of the MCDA performance evaluation

In order to evaluate the effectiveness of the groundwater potential model obtained, it is important to validate the result by comparing it with in situ aquifer measurement. According to Mogaji and Omobude (2017), validation is a method for ensuring the reliability of any proposed support system for decisions. The groundwater yield index map produced was validated using the borehole yield values obtained from a total of 124 boreholes. Using a qualitative comparison tool, the projected potential zone map (Fig. 10) was compared to the borehole yield map (Fig. 11). Table 4a, b summarizes the results of the validation. The GWYI map’s prediction accuracy was evaluated quantitatively and found to be 70% predictable. Superimposing the obtained groundwater potential map on the geological map of the study, zones of high and medium potentials correlate with areas underlain by sedimentary rocks. A high potential zone was also observed within the migmatite and migmatite gneiss terrain, and this can be related to the heterogeneity of migmatitic rocks. Granites and granite gneiss were observed to exhibit low groundwater potential, and this can be attributed to a low rate of fracturing in these rocks. In general, the result suggested that geology plays an important factor in the groundwater potential of the study area.

Fig. 11
figure 11

Borehole yield across the study area

Full size image
Table 4 The spatial attribute comparative scheme qualitative result
Full size table

Conclusions

A combined geophysical, hydrogeological and MCDA-AHP GIS modeling approach has been used to predict groundwater potential within Lokoja and its environs. One hundred and twenty-four (124) VES data and aquifer information from the existing borehole were obtained. In the context of AHP, a multi-criteria decision analysis (MCDA) methodology was used to characterize the estimated geo-electric parameters to define suitable areas for groundwater exploration. To evaluate the model’s predictive ability, the decision support model map produced was compared with the in situ borehole yield values. The result obtained shows that the application of GIS and geophysical techniques has proven to be an effective and inexpensive method of characterizing and assessing the aquifer system. The darzarock parameters estimated from VES data reveal aquiver resistivity, aquifer thickness, transverse resistance and coefficient of anisotropy values varying from 11 to 250 Ωm, 2.1 to 55 m, 140 to 5891 Ωm2 and 0.6 to 1.8, respectively, within the study area. The spatial distribution maps reveal that the central part of the study area is characterized by low resistivity, thereby inferring a good aquifer potential. 60%, 35% and 5% of the study area exhibit moderate, low and high aquifer thickness values, respectively. The coefficient of anisotropy value obtained within the sedimentary terrains confirms the availability of primary porosity in sedimentary rock as compared to basement rocks. The dominant groundwater flow direction was revealed to be toward the eastern direction. The groundwater potential map generated was able to classify the study area into low, medium and high yield zones. Areas with medium potential zones dominate the largest part of the study area having 66% area coverage with low and high zones having 22% and 10%, respectively. Comparing the potential map to the geology map of the study region, it was discovered that sedimentary rock underpins the high and medium potential zones. Within the migmatite and migmatite gneiss terrain, a high potential zone was also discovered. Undifferentiated granite and granite gneiss were found to highlight the low potential region. The study shows that geology plays a significant role in the possible occurrence of groundwater in the subsurface. The validation carried out on the proposed model reveals a 70% prediction accuracy.