Introduction

There are inherent connections among headwaters, landscape systems and downstream waters, and these causal relationships influence water supply, as well as the transport and fate of water and solute in watersheds (Alexander et al. 2007). According to Richardson (2020), headwater catchments constitute the originating streams of all river basins at their initiation stages. They can make up as much as 80% of the total stream length, and they can be very susceptible to pollutants, landscape dynamics and climate anomalies due to their small size and water volume (OHI 2014; Richardson 2020).

Potential evapotranspiration (PET) is an important component of the hydrological system, because it combines changes in many other climate parameters including temperature, radiation, humidity and wind speed (Zou et al. 2017). It is expedient to quantify evapotranspiration at river basin level for water resources management; this is because it directly influences the hydrologic water balance, which further informs the design of irrigation and drainage canals, reservoir operation, potentials for rain-fed agricultural production and crop water requirements of the basin (Dinpashoh 2006). Therefore, it becomes apparent to develop robust decision support tools for predicting PET in headwater catchments in order to manage water resources effectively.

Potential evapotranspiration represents water loss, water unavailable for exploitation by man and hence it plays an important role in water resource management and hydrological cycle because it is the main source of atmospheric moisture. At global and continental scales, evapotranspiration is the second largest component of the terrestrial water budget after precipitation (Glenn et al. 2007). Evapotranspiration transfers a large volume of water from soil and vegetation into the atmosphere (Anderson et al. 2012). About 60% of the global annual land precipitation is lost to it, while water loss from vegetation constitutes about 80% of terrestrial evapotranspiration (Glenn et al. 2007). It also serves as a form of sink in groundwater models since they remove water from the groundwater system. Therefore, efforts to ensure water resources sustainability cannot succeed without a proper understanding of the amount of water lost to evapotranspiration. Since it is very difficult to quantify, the derivation of numerical models for its predictions is a crucial step in water resources management.

Numerical models are adapted to mimic systems in order to predict their response to changes, exclusive of the quantification of the processes and physical characteristics of those systems. Since potential evapotranspiration is contingent on several interconnected weather variables, such as temperature, atmospheric water content, radiation, and wind speed, it is challenging for linear models to efficiently convey all its associated physical processes (Yassin et al. 2016; Yin et al. 2016). In this sense, the effective method to handle such nonlinear interaction between climate (independent) variables and potential evapotranspiration (dependent/response variable) are the utilizations of artificial intelligence and data-driven models (Wu et al. 2020). One data-driven algorithm that has recently gained popularity in the field of water resources management is the Random Forest (RF).

The RF algorithm was developed  by Breiman (2001), and it is classified as an algorithm of learning that include some of the most popular aggregation systems. RF algorithms combine multiple poor learners, these learners being decision trees (Scornet 2017). A series of separate trees are constructed to represent a single data set by adding randomness into the original method of tree construction. RF forecast is then calculated as the average of  all the tree forecasts (Scornet 2017). As these random forests seem to be capable of detecting related characteristics even in noisy settings, they are very versatile to handle complex feature spaces, as a result, the algorithm has been found useful in different fields such as ecology, bioinformatics, chemoinformatics and object tracking and recognition to mention a few (Scornet 2017).

RF has many advantages which include its fantastic lenience for outliers and noise, its difficulty in generating an over-fitting phenomenon, the ability to overcome the limitations of the “black-box” concept and its advantages of evaluating important features (Wu et al. 2020). With respect to approximating water resources, RF has been used by various researchers worldwide, for instance, Wu et al. (2020) evaluated the potentiality of RF in modeling potential evapotranspiration of an arid oasis region in China using some selected meteorological variable as input, while Wang et al. (2015) recommended the RF model for evaluating flood hazard risk in Dongjiang River Basin of China, both studies showed that RF was able to achieve satisfactory results. Additionally, Feng et al. (2017) compared RF and generalized regression neural networks (GRNN) models for approximating potential evapotranspiration estimates in southwest China, and discovered that RF model performed better than GRNN model.

RF model has demonstrated substantial potential in many studies. However, the utilization of the RF model for predicting PET of headwater catchments is relatively new, especially for river basins in Nigeria. Recently, various researchers have endeavored to assess the most important input feature combinations for optimizing the prediction of PET (Wu et al., 2020; Tao et al., 2018; Mattar 2018; Khoshravesh et al., 2015). For instance, temperature and relative humidity were reported to be the most important factors for predicting PET by Huo et al. (2012), while the utilization of the only temperature in predicting PET was discouraged by Wu et al. (2020). In many cases, the important input features are used in future model development, while the less important input features are disregarded. Therefore, researchers fail to ascertain the impact of adding or removing input features on model performance. As a result, the present study endeavors to close this gap in knowledge, by evaluating the most suitable feature combinations for building a reliable potential evapotranspiration (PET) model in the headwater catchments of Ogun River Basin. As well as to investigate the impact of the addition and deletion of input features on model performance. The objectives of the study are 1) to develop RF model for predicting PET in the study area, 2) to evaluate the performance of the developed RF model, 3) to evaluate the importance of climate parameters in the predicting PET of the study area, and 4) to investigate the impact of adapting or disregarding input features (based on their level of importance) on model performance.

Materials and methods

Description of study area

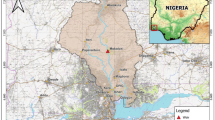
Ogun River Basin is a major river basin in the southwestern region of Nigeria. It is located within latitudes 6ο 33' N and 8ο 58' N; and longitudes 2ο 28' E and 4ο 8' E and encompasses a spatial extent of approximately 23,700 square kilometers (Oke et al., 2015). River Ogun takes its source from the Iganran Hills at an altitude of about 503 m east of Saki and flows for about 410 km before discharging into the Lagos Lagoon (Fig. 1a). In terms of physiography the basin area is distinguished as the upper-central basin to the north and lower basin to the south of Abeokuta. It is characterized by a tropical climate, two maxima rainfall pattern (Adediji and Ajibade 2008) and high varying temperature both spatial and temporally. The study area is the northern headwater catchment of Ogun River Basin (Fig. 1b), which is made up of a network of headwater sub-basins of the Ogun, Okifi and Oyan Rivers . As shown in the map (Fig. 1b), this area is largely composed of 1st, 2ndand 3rdorder streams.

Fig. 1
figure 1

Map of Ogun River Basin area showing the major tributaries (a) and Northern Headwater Catchment (b)

Full size image

Data acquisition

Meteorological data were obtained from the Nigeria Meteorological Agency (NIMET) for Saki station (Fig. 1b), which is the main meteorological station located in Ogun headwater catchments. The meteorological parameters obtained at these stations included maximum and minimum temperature, relative humidity, sunshine duration and wind speed at two meters, which were required for the computation of potential evapotranspiration. The time series of the obtained meteorological data span over a period of 33 years (1984–2016). No missing data were found in the time series.

FAO penman–monteith (FAO P-M) method

The study adopts the FAO P-M method, which has been recommended as the main standard scheme for the estimating evapotranspiration. This method was chosen because its essential data are available, and because of its robustness. It is relatively complete in theory, considers a wide-range of various climatic factors affecting evapotranspiration, and its accuracy and reliability have been confirmed in several regions around the globe (Xin-e et al. 2015). The FAO P-M method is represented by Eq. 1:

$${\text{ET}}_{0} = \frac{{0.408\Delta \left( {R_{n} - ~G} \right)~ + ~\gamma \left[ {\frac{{900}}{{\left( {T_{{{\text{mean}} + 273}} } \right)}}} \right]U_{2} \left( {e_{s} - e_{a} } \right)}}{{\Delta + \gamma \left( {1 + 0.34U_{2} } \right)}}$$
(1)

where ET0 is reference evapotranspiration (mm), ∆ is the slope of the saturated vapor pressure (kPa/C0), Rn is the net radiation at the crop surface (MJ/(m2d)), G is the soil heat flux density(MJ/(m2d)), T mean is the mean monthly air temperature at a height of 2 m (C0), u2 is wind speed at a height of 2 m (m/s), es-ea is the saturation vapor pressure deficit (kPa), and g is the psychrometric constant (kPa/C0).

Random forest (RF) method

RF is based on Classification and Regression Trees (CART) model. The nucleus of the RF is centered on the extraction of a repeated random K sample from a unique training sample set N for generating a new set of training samples through the bootstrap resampling method. Thereafter K decision trees are generated and the bootstrap sample collection forms a random forest.

With respect to a classification problem, a classified outcome of novel data depends on the quantity of votes obtained by classification tree votes, and in the case of a regression problem, all the averages of the predictive value of decision trees are regarded as final prediction outcomes (Fig. 2).The description of the variant, parameters, and feature importance capabilities of RF and its functioning procedure has been detailed in the work Boulesteix et al. (2012), Scornet (2017) and Wu et al. (2020).

Fig. 2
figure 2

Adapted from Wu et al., 2020)

Workflow diagram of a random forest (

Full size image

Since the estimated potential evapotranspiration are continuous values, a supervised regression framework was considered in this study, which entails the development of an optimized model for predicting potential evapotranspiration in the study area. Where the computed monthly potential evapotranspiration (PET) represents the dependent variable while rainfall (R), wind speed (U), sunshine hour (S), relative humidity (Rh), minimum temperature (Tmin) and maximum temperature (Tmax) are the predictors as shown in Eq. 2:

$${\text{PET}} = {\text{ }}f{\text{ }}\left( {R,{\text{ }}U_{2} ,{\text{ }}S,{\text{ Rh}},{\text{ }}T\min ,{\text{ }}T\max } \right)$$
(2)

The model was developed using the "random forest" package written in R statistical software (http://www.R-project.org version 3.6). The random forest was calibrated using 70% of the dataset, while the remaining 30% served as the validation set. It is widely speculated that 'ntree', which signifies quantity of trees in the forest, and ‘mtry' which signifies the number of distinct descriptors verified based on respective partition, are important parameters for calibrating RF models (Li et al. 2016; Scornet 2017; Rakhee et al. 2020; Aiyelokun et al. 2021). A ntree of 350, mtry of 5 were found to be adequate for building the model used in this study.

Evaluation of model performance

The performance of the model was assessed using mean absolute relative error (MEA), coefficient of determination (R2) and Nash–Sutcliffe efficiency coefficient (NSCE). A low MEA value, and R2 and NSCE value close to 1 are evidence of a good model. The mathematical descriptions  of MEA, R2, and NSCE are listed as follows:

$${\text{MAE}} = \frac{{\mathop \sum \nolimits_{1}^{n} \left( {y_{i} - \tilde{y}_{i} } \right)}}{n}/\tilde{y}_{i}$$
(3)
$$R^{2} = \mathop \sum \limits_{{i = 1}}^{n} \left[ {\left( {y_{i} - \bar{y}_{i} } \right)\left( {\tilde{y}_{i} - \overline{{\tilde{y}}} _{i} } \right)} \right]^{2} /\left[ {\mathop \sum \limits_{{i = 1}}^{n} \left( {y_{i} - \bar{y}} \right)^{2} \mathop \sum \limits_{{i = 1}}^{n} \left( {\tilde{y}_{i} - \overline{{\tilde{y}}} _{i} } \right)^{2} } \right]$$
(4)
$${\text{NSCE}} = 1 - \mathop \sum \limits_{{i = 1}}^{n} \left( {y_{i} - \tilde{y}_{i} } \right)^{2} /\mathop \sum \limits_{{i = 1}}^{n} \left( {y_{i} - \bar{y}} \right)^{2}$$
(5)

where \(y_{i}\) is the estimated PET, \(\tilde{y}_{i} ~\) is the predicted PET, while \(\bar{y}{\text{~and}}\overline{{\widetilde{{~y}}}} _{i}\) indicate the average observed and predicted PET, respectively. The terms ‘training’ and ‘testing’ phases used for the data intelligent model also means calibration and validation of physically based hydrological model (Li et al. 2016). These evaluation criteria were chosen because of their wild application in hydrological model evaluation.

Important feature selection methods of random forest

The random forest has great potential in dealing with data that has outliers and noise, this makes it efficient as an important feature assessment tool (Jaiswal and Samikannu 2017). The important feature section capability of RF puts it in the frontline compared to numerous algorithms used for generating insights during data-driven model development. The study used two important feature selection methods of RF which include minimal depth (Ehrlinger 2015; Ishwaran et al. 2010) and percentage increase in mean square error (%IncMSE) (Zhang et al. 2018).

Minimum depth distribution

The minimal depth distribution is an important technique for ranking the predictors used for constructing a RF model. The minimum depth method is based on the assumption that the nodes of predictor variables with high influence on the response variable are frequently split close to the root node (tree trunks) (Ehrlinger, 2015). The relative distance of a node to the trunk of the tree determines the numeric attributes which the node takes, while the root node takes zero (Ehrlinger 2015). The minimum depth evaluates the essential risk factors by taking an average of depth of all first split of individual variable against all the trees in the forest, such that the important variables have shorter distance to the root (Ehrlinger 2015). In summary, the minimal depth of a variable is a proxy measure of predictive strength of the variable. The lesser the minimal depth, the more influence the variable has in cataloging observations, and consequently on the forest accuracy.

Percentage increase in mean square error (%IncMSE)

Percentage increase in Mean Square Error (%IncMSE) is the most efficient and revealing method for identifying important variables from RF. The important features in prediction have the highest percent increase in MSE after the data have been permutated (Zhang et al 2018). The level of significance of the %IncMSE was further assessed based on the permutation of the response variable. This involves the development of a RF model to measure the feature importance, thereafter the response variable is permuted n number of times, while new RF models are being developed for each n step, as the p values of each predictor (feature) is estimated. P value of less than 0.05 is considered to be more likely to significantly affect the model predictive performance.

The summary of the steps used in conducting the study based on the methodology is presented in Fig. 3.

Fig. 3
figure 3

General methodological framework

Full size image

Result and discussion

Performance evaluation of RF model

The importance of determining PET with reliable accuracy cannot be overstated in water resources management, especially in water-scarce regions (Nourani et al. 2020). This study endeavors to establish a highly reliable RF model for predicting PET which is an important variable in the management of water resources. The functioning of the developed RF model was evaluated using evaluation criteria of MAE, R2 and NSCE as presented in Table 1. It could be observed that there was a small average absolute difference between the observed and predicted PET based on the calibration and validation MAE, while a coefficient of determination of 0.98 and 0.92, respectively, for the calibration and validation phase is an indication of a good fit between the modeled and the observed PET. Furthermore, the NSEC of the model is very close to 1 at both calibration and validation phase, indicating that RF model is adequate for predicting PET in the study area.

Table 1 Summary of performance of random forest models
Full size table

This result corroborates various other studies that have been conducted to evaluate the performance of RF in predicting PET. For instance, Rakhee (2020) observed that RF forest performed better than logistic regression and discriminate analysis in predicting evapotranspiration. Wu et al. (2020) developed RF models with different input combinations that were able to achieve satisfactory results at calibration and validation phases. In their study, the R2 of the models ranged from 0.962 to 0.996 at the calibration phase and 0.909–0.990 at validation phase. Similarly, Feng et al. (2017) established that RF model with complete data input constituting of maximum temperature, minimum temperature, solar radiation, wind speed, relative humidity and extraterrestrial radiation performed better (NSCE of 0.958 ∼ 0.990) than RF models with incomplete input data (maximum, minimum air temperature and extraterrestrial radiation) with NSCE ranging from 0.862 to 0.951. Generally, since the R2 and NSCE at both calibration and validation phases (Table 1) are greater than 0.70, it can be concluded that the results of the RF model is acceptable.

The agreement between the observed and the predicted PET at the calibration and validation phase was examined by combining scatter and time series plots as shown, respectively, in Fig. 4 and Fig. 5. Both combinations of plots show that there is a close agreement between observed and predicted PET; for instance, the predicted PET follows the patterns of the observed PET very closely. It is obvious that the model underestimated extreme low and high PET in some months at both calibration and validation phase. In the study area, PET are usually high in part of the dry seasons between January and March and are usually low in part of the wet season between July and September (Egwuonwu et al. 2012; Ashaolu and Iroye 2018). This implies RF underestimated PET mostly in the wettest and driest months as could be seen in Figs. 4 and 5. A similar case was reported by Feng et al. (2017), who observed that RF models of different input combinations underestimated PET between March and August and overestimated PET between September and December. This is an indication that RF may be sensitive to extreme values of PET and their predictor, in agreement with the study of Wu et al. (2020), which concluded that models may find it difficult to explain minimum and maximum PET perfectly.

Fig. 4
figure 4

Summary of agreement between observed and predicted PET at calibration phase based on scatter and time series plot

Full size image
Fig. 5
figure 5

Summary of agreement between observed and predicted PET at validation phase based on scatter and time series plot

Full size image

Evaluation of features importance in predicting PET

The evaluation of important climate parameters in predicting the PET of Ogun Headwater catchments was assessed using the minimum depth plot (Fig. 5) and the analysis of the increase in MSE with their level of significance (Table 2). Based on Fig. 6, maximum temperature and relative humidity have the lowest mean minimum depth of 1.04 and 1.42, respectively, with less than 100 trees. Sunshine duration and wind speed have a mean minimum depth of tress of 1.80 and 2.06, respectively, while minimum temperature and rainfall had the highest mean minimum depth of trees of 2.15 and 2.49, respectively. This is further established in Table 2, which shows the climate variables were important in the prediction of PET in the order of Tmax > Rh > U2 > S > R > Tmin based on their values of IncMSE%. This implies that Tmax, Rh, U2 and S are important variables in predicting PET of the study area. However, since the p values of Tmax and Rh were lesser than 0.05, then they could be considered to be the most important variables for predicting PET in Ogun headwater catchments.

Table 2 Statistical evaluation of important climate parameters in predicting PET
Full size table

Similar results have been obtained in previous studies. For instance, Huo et al. (2012) revealed that temperature and relative humidity were the most important factors affecting PET, while Wu et al. (2020) have also confirmed that using temperature only is not sufficient for predicting PET, their study established that in support of previous closely related studies; sunshine hour, wind speed and relative humidity play a significant role in reducing model errors when predicting PET. In contrast to previous studies (Wu et al. 2020; Tao et al. 2018; Mattar 2018; Khoshravesh et al. 2015), the present study discovers that minimum temperature is not important in determining PET. While rainfall was also found to be unimportant in PET prediction, which could have been the reason why rainfall has been ignored by many researchers when constructing input features for building PET models.

Having established that minimum temperature and rainfall were not important features for model development; different combinations of the important features were thereafter used to build RF models. This was done to examine the impact of these combinations on the reliability of predicting PET in the study area. As shown in Table 3, RF model developed using the most important variables (Tmax and Rh with p value < 0.05) performed less in comparison with the results of the initial combination presented in Table 2. This shows that the utilization of features with high IncMSE% and statistical significance (p value < 0.05) may not achieve more accurate model. As a result, statistically non-significant features should not be disregarded without further evaluation when building RF models. Generally, the RF model that combines features with high IncMSE% and low minimum depth (Fig. 6) achieved the overall best performance as shown in Fig. 7.

Table 3 Performance of RF models based on different combinations of importance feature
Full size table
Fig. 6
figure 6

Distribution of minimum depth and mean of maximum temperature (Tmax), relative humidity (Rh), sunshine duration (S), wind speed (U2), minimum temperature (Tmin) and rainfall

Full size image
Fig. 7
figure 7

Comparison of model errors based on different combination of important features

Full size image

Therefore, it could be inferred from the foregoing analysis that model combinations that have wind speed and sunshine hour in combination with maximum temperature as input features, achieved the least generalization error (MAE of 2.52 and 6.29, respectively, at calibration and validation phase) and highest R2 and NSCE values. This is in agreement with Martí et al. (2015) who revealed that high percentage of variations in PET is determined by temperature and solar radiation, and Feng et al. (2014) who unraveled that sunshine hour is important when developing models to predict PET.

Conclusion

Headwater catchments play important roles in the sustainability of water resource processes of a river basin. In this study, an attempt was made to present the most suitable feature combinations for building a reliable PET model in the headwater catchments of Ogun River Basin, Southwest Nigeria. It was established that RF with a combination of four parameters (maximum temperature, relative humidity, sunshine duration and wind speed) can successfully model PET in the study area with high accuracy. However, in contrast to previous studies where different combinations of model inputs were assessed to ascertain best combinations. The present study evaluated the performance of different models based on the combinations of already established important features, taking cognizance of the effects of adapting or disregarding input features of climate parameters (with respect to their level of importance). This approach was shown to yield satisfactory results for the study area. Based on the results presented in this study, RF is offered as a decision support tool that can be used to accurately predict PET in headwater catchments and data-limited areas. This method can be applied to inform decision-making in water resources management of the study area and other parts of the world.