Introduction

It is of utmost importance as also of societal concern about the large-scale depletion of natural resources as also the environmental regulations which have diverted the attention of people in search for getting clean air, soil and water. In textile industry, it is of great concern to reduce the consumption of water as also reducing carbon footprint (Zaffalon 2010). The current value of textile industry which placed at around US$ 120 billion is likely to reach US$ 230 billion in 2020. This industry, in its magnitude, is next only to agriculture in employing man power engaging over 45 million people directly and 20 million people indirectly. Textile industry contributes 2 percent to India’s gross domestic product and 14 percent to overall index of industrial production. There are two sectors which are operating in textile industry. The first one is the organized sector which comprises spinning; apparel and garments use modern machinery and techniques. As against this, the second is the unorganized sector comprising handloom, handicrafts and sericulture which usually operate on small scale and use only traditional tools and methods (www.ibef.org). Between these, the latter uses old machineries, adopts out-dated technologies and uses variety of synthetic dyes ultimately leading to environmental or more precisely water pollution.

Azo dyes constituting the largest class of synthetic dyes are integral part of textile industry and make up to about 70% of commercial dyes (Hubbe et al. 2011). They are extensively used for dyeing cloths and are used at 60 °C, while majority of other dyes need boiling temperature. These dyes are valued much since they offer wide range of colors, provide extreme color fastness and the intensity of color is much more than any nearest alternative, thereby making them invaluable to the textile industry (Carliell et al. 1998). Azo dyes are characterized by structures with one or more azo group (–N=N–) that are bound to the aromatic rings having recalcitrant molecular structure. Under certain circumstances, the azo groups are subject to cleave producing potentially harmful aromatic amines (de Lima et al. 2007). Hence, the removal of these dyes from wastewater by any usual biological, chemical and physical methods is of paramount importance. Although several methods have been reported, they are having such limitations as high cost of plant and machinery, non-affordable operational costs, regeneration, secondary pollutants, sensitivity toward waste water contents, interference by extraneous waste water constituents and residual sludge generation (Szyguła et al. 2008; Dávila-Jiménez et al. 2005).

Acid blue 113 (AB113) is categorized as bis-azo dye which is extensively used for dyeing wool, silk and polyamide fibers from a neutral or acid bath to obtain deep shade of navy blue color (Green 1990). There is limited information reported about its decoloration, degradation and/or adsorption from water. Based on the techniques, methods and procedures reported, these could be classified into six broad categories which include biological-cum-chemical (Eskandarian et al. 2014; Lee et al. 2015; Khehra et al. 2005; Srinivasan and Mishra 2008; Husain et al. 2010), electrocoagulation (Saravanan et al. 2010), physical methods using UV radiation (Shu et al. 2015, 2016a, b; Shu et al. 2005; Rai et al. 2013), photocatalytic degradation (Thejaswini and Prabhakaran 2016; Zayani et al. 2008), low frequency ultrasound-assisted degradation (Sathishkumar et al. 2014), nanomaterials (Shu et al. 2016c) and use of inorganic materials including activated carbons (Gupta et al. 2011; Shu et al. 2010; Shirzad-Siboni et al. 2014; Pura and Atun 2009; Shokohi et al. 2011; Talwar et al. 2016). Reports are lacking on the application of agro-based biological materials for the remediation of AB113 from water.

The growing demand for nutraceuticals across the world as alternative to allopath or modern systems of medicine has attracted the attention of many industries including the pharmaceuticals. Transformations in food habits, less physical activity and increasing desk-oriented jobs have made vulnerable the lifestyle ailments. The common urban and semi-urban populations are becoming more aware about their health and fitness. This is providing a massive growth opportunity for expanding nutraceuticals in India. According to the Associated Chambers of Commerce and Industry of India, the Indian nutraceuticals market is growing from $ 4 Bn in 2015 to $ 10 Bn in 2022. This represents a remarkable growth rate of 21% annually (www.mrssindia.com). Disposal of the spent which amounts to 50–95% of the total quantity of herbs, shrubs, seeds and/or roots processed and together totally termed as Nutraceutical Industrial Spent (NIS) is posing a challenge for the industry. The peculiarity of the spent is that they cannot be used either as manure or as an animal feed due to the chemicals used while processing. Subjecting the spent to use as a fuel in furnace is a feasible proposition, but the problem of environment pollution as greenhouse gases comes as a problem.

Our research school is the first to undertake investigations on the use of NIS as filler material in the fabrication of thermoplastic and thermoset composites (Taqui et al. 2019; Syed and Syed 2016a, b; Syed and Syed 2012; Pashaei et al. 2011; Syed et al. 2010a, b, 2011; Syed et al. 2009). We have also taken a lead in using NIS as adsorbent for remediation of Congo red, methylene blue and ethidium bromide dyes (Taqui et al. 2017; Papegowda and Syed 2017; Sulthana et al. 2018). Despite myriad research papers reporting on the use of low-cost agricultural waste materials as biosorbents for the remediation of toxic dyes, very limited information is available on the utilization of dye-adsorbed biosorbent or ‘sludge.’ We have directed our effort also on the use of ‘sludge’ as filler material in the fabrication of thermoplastics and thermosets (Taqui et al. 2019).

Seeds of fenugreek (Trigonella foenum-graecum L., Leguminosae family) have been categorized as nutraceuticals. It is the oldest medicinal plant, originated in India and as well as in North Africa. It is an annual plant, growing about two feet height. Both leaves and seeds are used for extraction. The powder of fenugreek seeds is also used as medicine. The plant extract possesses many therapeutic properties, of which pain relief, anti-inflammation, laxative and antispasmodic are important. It is also used as anticancer and diabetic carminative, heart tonic, hypertension decreasing, triglyceride lowering, breast milk increasing, oxytocic and sexual desire enhancer (Smith 2003).

India is the largest producer of fenugreek in the world, and the average production during 2011–12 was 121,775 tons (Vidyashankar 2014). The seed is traded as a spice and oil extracted as oleoresin. Oleoresin constitutes about 50% of the total weight of fenugreek seed. The remaining portion of the seed is discarded as spent, commonly known as nutraceutical industrial fenugreek seed spent (NIFGS). The porous structure of spent traps moisture and decreases the calorific value. This property has, however, been exploited to use it as a potential adsorbent for remediation of AB113 dye from water. Images of fenugreek seeds and fenugreek seed spent are shown in Fig. 1a, b, respectively.

Fig. 1
figure 1

a Fenugreek seed and b nutraceutical industrial fenugreek seed spent

Full size image

Materials and methods

Materials

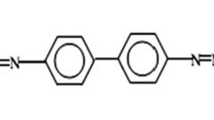
Acid blue 113 (AB113) was procured from Sigma-Aldrich, India. Chemical formula = C32H21N5Na2O6S2; molecular weight = 681.65; absorbance maximum (λmax) = 566 nm. The structure of AB113 dye is shown in Fig. 2.

Fig. 2
figure 2

Structure of Acid blue 113

Full size image

Adsorbent preparation and characterization

Adsorbent preparation

NIFGS procured from a local factory was initially dried in sunlight, crushed and finally ground using a ball mill and sieved to get ASTM standard particle size: (≤ 90, ≥ 90 ≤ 125, ≥ 125 ≤ 177, ≥ 177 ≤ 355, ≥ 355 ≤ 500, ≥ 500 ≤ 710 µm).

Surface characterization, batch adsorption experiments, adsorption kinetics and statistical optimization of process parameters

The experimental details regarding surface characterization (SEM, IR and point of zero charge), batch adsorption experiments, adsorption isotherms, adsorption kinetics and statistical optimization of process parameters are shown in Table 1, and the details are reported elsewhere (Dhaif-Allah et al. 2019).

Table 1 Factors considered for experimental design along with their high and low levels
Full size table

Results and discussion

Characterization of the adsorbent

Surface characterization of NIFGS done through SEM exhibited slightly porous structure (Fig. 3a). Upon adsorption (Fig. 3b) of AB113 dye, some pores got completely filled with the adsorbate forming a thin film over the particle. IR spectra of NIFGS (Fig. 4) provided that the absorption at 3299 cm−1 is due to stretching of hydroxyl groups of cellulose, hemicellulose and lignin present in NIFGS. The band at 2967 cm−1 is due to the C–H stretching of saturated carbon. The bands at 1635 cm−1 are due to C=C stretching. The bands at 1163 cm−1 and 1038 cm−1 are assigned to C–O vibrations and O–H bending, respectively. The finger print region of the biological material NIFGS indicates complex bands, and accurate assignment of the peaks is difficult in the absence of standard sample. However, the presence of cellulose and lignin indicates that the spent has hydrophilic and hydrophobic properties. Determination of point of zero charge at intersection of two plots (Fig. 5) confirms that at pH 7.1 the adsorbent surface has zero charge.

Fig. 3
figure 3

a SEM image of NIFGS and b SEM image of AB113 adsorbed NIFGS

Full size image
Fig. 4
figure 4

FTIR spectra of AB113, NIFGS and AB113 adsorbed on NIFGS

Full size image
Fig. 5
figure 5

Point of zero charge of NIFGS at the intersection

Full size image

Effect of pH, initial dye concentration, adsorbent dosage, adsorbent particle size and temperature

The effect of different parameters on batch adsorption studies of NIFGS had shown remarkable similarities with our earlier reported studies (Dhaif-Allah et al. 2019). Adsorption capacity observed at pH 2 was maximum (Fig. 6a), and significant decrease in adsorption occurred when pH was increased from 2 to 4. Thereafter, marginal change in adsorption was noticed up to pH 12. Maximum AB113 dye removal by NIFGS was at pH 2.0 (qe= 91.00 mg g−1) with initial concentration of 100 µg ml−1. Initial dye concentration versus qe and % qe is shown in Fig. 6b. The effect of adsorbent dosage was similar to the studies reported by us (Dhaif-Allah et al. 2019). The results are illustrated in Fig. 6c. Adsorption capacity was maximum for initial AB113 dye concentration of 100 µg ml−1 at neutral pH. The particle size of ≤ 90 µm; ≥ 90 µm ≤ 125 µm; ≥ 125 µm ≤ 177 µm; ≥ 177 µm ≤ 355 µm; ≥ 355 µm ≤ 500 µm and ≥ 500 µm ≤ 710 µm in which the adsorption of dye decreased with the increase in the size of the adsorbent particle size (Fig. 6d). The observation is in conformity with the universal fact that surface area decreases with increase in particle size. The size ≥ 125 µm ≤ 177 µm (80 mesh ASTM) was selected for further studies because 80 mesh particle is commonly used in the fabrication of composites and sieving lower size particles takes more time and adds additional cost to the process. The influence of temperature on adsorption was studied at 30–50 °C with three dye concentrations. Figure 6e shows that increase in temperature decreases adsorption rate indicating that it is an endothermic process (Chowdhury and Das 2012).

Fig. 6
figure 6

Effect of a pH, b initial dye concentration, c adsorbent dosage, d particle size and e temperature onto adsorption of dye onto AB113-NIFSS system

Full size image

Adsorption isotherm

Adsorption isotherm parameters are useful to know the interactions of adsorbate molecules with adsorbent surface. This is achieved through Langmuir and Freundlich isotherm models by predicting the adsorption capacities. The implication of Langmuir isotherm model is that the adsorption process is monolayer process which happens on the surface of adsorbent, and it involves finite number of similar adsorption sites processing uniform energies (Langmuir 1916). The equation used for this is as follows:

$$q_{\text{e}} = \frac{{Q_{\text{m}} K_{\text{a}} C_{\text{e}} }}{{1 + K_{\text{a}} C_{\text{e}} }}\quad R_{L} = \frac{1}{{1 + K_{\text{a}} C_{0} }}$$
(1)

Here, qe implies quantity of dye adsorbed by adsorbent (mg g−1) under equilibrium condition; Ce is the equilibrium concentration (µg ml−1). Intercept and slope of qe versus Ce determine the value of Qm and Ka, The monolayer adsorption capacity (mg g−1) is determined by Qm, and Ka is the Langmuir constant (L mg−1) which has relation to free energy of adsorption. The equilibrium experiments conducted with initial AB113 concentrations of 25–400 µg ml−1 gave the Qm value as 439.06 mg g−1 for the isotherm, and it is higher compared to experimental qe value of 91.00 mg g−1. But, the R2 value of 0.96 infers a good fitting of this isotherm to the experimental data. The RL separation factor of the Langmuir isotherm (Webber and Chakkravorti 1974) was between 0.677 and 0.116, indicating favorable adsorption of AB113 on to NIFGS. The values of RL indicate whether the adsorption is unfavorable (RL> 1), linear (RL= 1), favorable (0 < RL< 1) or irreversible (RL= 0). Lowering of RL with consequent increase in initial concentration indicates higher adsorption at higher temperature. The large difference between Qm (439.06 mg g−1) and qe (91.00 mg g−1) is not very much favorable. Hence, Freundlich isotherm model was tried.

Freundlich isotherm model suggests that the adsorption process takes place on a heterogeneous surface (Freundlich 1906). In the present study, the adsorption capacity of NIFGS is related to AB113 dye concentration at equilibrium, and this is shown by following equation:

$$q_{\text{e}} = K_{\text{F}} C_{\text{e}}^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {n_{\text{F}} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${n_{\text{F}} }$}}}}$$
(2)

Here, KF and nF signify Freundlich constants in relation to capacity for adsorption [mg g−1] and intensity of adsorption [mg/L)−1/n], respectively. Heterogeneity factor (nF) is the name for latter. This indicates whether the adsorption is linear (nF= 1), chemisorption (nF< 1) or physisorption (nF> 1). The values of nF and 1/nF in the present study are 1.798 and 0.556, respectively, which indicate that the process is physisorption. KF and nF are calculated from the intercept and slope of the plot ln qe versus ln Ce. The fitting of Freundlich isotherm to the experimental data has given a R2 value of 0.93 which implies that it is linear process. Hence, the adsorption of AB113 dye on to NIFGS is favorable and the process is physisorption. But from Langmuir and Freundlich models, no definite inference was obtained with respect to homogeneity or heterogeneity of the process of adsorption. Therefore, Jovanovic isotherm (Jovanović 1969) model was tried and the equation for Jovanovic model is

$$q_{\text{e}} = Q_{\text{m}} (1 - e^{{(K_{\text{J}} C_{\text{e}} )}} )$$
(3)

Kj represents Jovanovic constant, qe is the quantum of dye adsorbed on to adsorbent (mg g−1) at equilibrium; equilibrium concentration (µg ml−1) of dye in solution is represented by Ce. This model signifies monolayer formation having no interactions. Deviation of results from Langmuir isotherm is denoted by Kj. According to this model, the value of Qm obtained is 316.94 mg g−1, which is higher than 91.00 mg g−1 obtained by the experiment. But it is lower than that obtained by Langmuir isotherm.

The equation for the isotherm model proposed by Dubinin–Radushkevich (Dubinin 1947) is as follows:

$$q_{\text{e}} = q_{\text{s}} [\exp ( - K_{\text{ad}} \varepsilon^{2} )]\quad {\text{where}}\quad \varepsilon = RT\ln \left[ {1 + \frac{1}{{C_{\text{e}} }}} \right].$$
(4)

In this equation, qs (mg g−1) has relation to adsorption capacity qe (mg g−1), Kad (mol2 kJ−2) is the average free energy of adsorption, R (J mol−1 K−1) and T (K) is denoted by absolute temperatures. The value realized is Qm=234.59 mg g−1 which is higher than the experimental value of qe = 91.00 mg g−1. R2 value, which indicates linearity, is 0.86. However, as the values of χ2 and R2 are closer, it is a better fit model than Langmuir model (Fig. 7a, b). The results presented in Tables 2, 3 and 4 prove that AB113 dye interacts with NIFGS linearly, and the reaction is physical and favorable.

Fig. 7
figure 7

Fitting of adsorption data to a Langmuir and Freundlich, b Jovanovic and Dubinin–Radushkevich, c Sips, Redlich–Petersen and Toth and d Vieth–Sladek and Brouers–Sotolongo adsorption isotherms

Full size image
Table 2 Calculated parameters of two-parameter isotherms
Full size table
Table 3 Calculated parameters of three-parameter isotherms
Full size table
Table 4 Statistical parameters for isotherm model fitting
Full size table

Toth, Sips, Radke–Prausnitz, Redlich–Peterson, Vieth–Sladek and Brouers–Sotolongo are six other three-parameter isotherm models which were also tried for academic interest.

The Toth isotherm (Toth 1971) is useful for heterogeneous adsorption system. In Table 4 and Fig. 7c, Qm value of 317.45 mg g−1 obtained is higher compared to experimental qe value of 91.00 mg g−1 but lower to Langmuir isotherm value of 439.06 mg g−1.

Sips isotherm (Sips 1948) depending upon the adsorbate concentration can be either Langmuir or Freundlich isotherm equation. The value Qm=413.09 mg g−1 in Sips isotherm deviates from experimental value R2= 0.96, SSE of 2707.6 and χ2 of 30.89 values making it a good fit.

The Redlich–Peterson isotherm model (Redlich and Peterson 1959) is improved version of Langmuir–Freundlich, and a correction factor ‘g’ is included. In the equation, Langmuir isotherm represents g = 1 and Freundlich isotherm is g = 0 and the ‘g’ value of 1.596 obtained indicates that adsorption is tending toward Langmuir isotherm. The equation of Redlich–Peterson isotherm is given as:

$$q_{\text{e}} = \frac{{A_{\text{RP}} C_{\text{e}} }}{{1 + B_{\text{RP}} C_{\text{e}}^{g} }}$$
(5)

ARP, BRP and g are Redlich–Peterson constants, qe is the quantity of dye being adsorbed (mg g−1) under equilibrium; equilibrium concentration (µg ml−1) of dye in solution is represented by Ce.

Vieth–Sladek isotherm (Vieth and Sladek 1965) is useful for such solutes which get adsorbed as per some specific isotherms which simplify linear component (Henry’s law) and nonlinear components (Langmuir equation) according to solute dissolved in adsorbents amorphous region. This model estimates rates of diffusion from transient adsorption in solid materials. The equation of this isotherm is:

$$q_{\text{e}} = K_{\text{VS}} C_{\text{e}} + \frac{{Q_{\text{m}} \beta_{\text{VS}} C_{\text{e}} }}{{1 + \beta_{\text{VS}} C_{\text{e}} }}$$
(6)

KVS and βVS are Vieth–Sladek constants, qe is the quantity of dye being adsorbed by the adsorbent (mg g−1) under equilibrium condition, maximum adsorption capacity is Qm, and Ce is the equilibrium concentration (µg ml−1) of the dye. In this study, the SSE value got is 2779.9, χ2 is 29.286 and R2 is 0.96. These make a good fit to the experimental values. The Qm value obtained is 439.06 mg g−1.

Brouers–Sotolongo isotherm (Brouers et al. 2005) is similar to that of Vieth–Sladek isotherm. The KBS and α in the equation represent adsorption power and active site distribution, respectively, of the adsorbent–adsorbate system. The equation is:

$$q_{\text{e}} = Q_{\text{m}} [(1 - \exp ( - K_{\text{BS}} (C_{\text{e}} )^{\alpha } )]$$
(7)

Here, KBS and α are Brouers–Sotolongo constants, amount of dye adsorbed by adsorbent (mg g−1) at equilibrium is denoted by qe, Qm is the maximum adsorption capacity, and equilibrium concentration (µg ml−1) of the dye in solution is indicated by Ce. The value of Qm obtained is 108.00 mg g−1 which is slightly higher than the experimental result of 91.00 mg g−1, and the R2 value of 0.97 is a good prediction to the experimental data (Fig. 7d).

These models discuss about more complicated equations but they definitely help in making the mechanism of adsorption more clear. The value of R2 alone cannot be considered for the experiment since it can be applied only for linear models. χ2 values, however, are applicable only if model data and experimental data are similar. The Qm, χ2 and R2 values of all the nine models are presented in Tables 4 and 5. The values of all these models as also the actual experimental data (qe) will provide useful guidance for further research to develop new models in solving adsorption phenomena occurring in AB113-NIFGS system.

Table 5 Experimentally determined and theoretically predicted parameters for absorption kinetic models
Full size table

Adsorption kinetics

Kinetic data obtained at 100, 150 and 200 µg ml−1 concentrations of AB113 dye and at 303 K, 313 K and 323 K temperature were analyzed using models proposed by Lagergren (1898), Ho and McKay (1998), Alkan et al. (2007), Wang et al. (2004) and Boyd et al. (1947) to collect information about their effect on adsorption rate. The parameters tested were analyzed by nonlinear analyses (MS Excel 2010), and the results are presented in Table 6. Pseudo-second-order model proposed by Ho and McKay has given the best fit at all the tested dye concentrations and temperatures investigated as evidenced by coefficient of determination (R2) and chi-square (χ2) values (Fig. 8a–c). Maximum adsorption took place in the beginning which gradually slowed down and thereafter remained almost constant. Higher temperature increased adsorption capacity (qe) marginally. The AB113 dye molecules moved from solution to the solid surface and then diffused into the pores of NIFGS. Thus, it may be inferred that multi-step adsorption which is not rate limiting has occurred. The observations made using Dumwald–Wagner model (Fig. 9a), Weber–Morris model (Fig. 9b) and film diffusion model (Fig. 9c) were similar to our earlier studies (Dhaif-Allah et al. 2019). The data in Table 6 conclusively prove that diffusion is a rate-limiting process.

Table 6 Calculated parameters for diffusion models
Full size table
Fig. 8
figure 8

Kinetic model fits for, a 100 µg ml−1, b 150 µg ml−1 and c 200 µg ml−1 initial dye concentration of AB113 on NIFGS system at different temperatures

Full size image
Fig. 9
figure 9

Kinetics data fitted to a Dumwald–Wagner, b Weber–Morris and c film diffusion models with initial concentration of AB113 dye: (A) 100 µg ml−1, (B) 150 µg ml−1, (C) 200 µg ml−1

Full size image

Adsorption thermodynamics

The thermodynamic parameters including ∆H°, ∆S° and Ea which were estimated using the slope and intercept of Van’t Hoff plots of ln(Kd) and ln(K2) versus 1/T are shown in Fig. 10a, b, respectively, and presented in Table 7. The interpretation of the data is as described in our paper (Dhaif-Allah et al. 2019). The activation energy values for initial concentrations of 100, 150 and 200 µg ml−1 as obtained by applying kinetic constant from pseudo-second-order model and Arrhenius equation ranged between ~ − 233.16 and 34.84 kJ mol−1.

Fig. 10: a
figure 10

Plot of thermodynamic equilibrium constant versus 1/T to determine the enthalpy and Gibbs free energy of the process. b Plot of pseudo-second-order kinetic constant versus 1/T to determine the activation energy of the process

Full size image
Table 7 Thermodynamic parameters of AB 113-FGS system
Full size table

Statistical optimization by fractional factorial experimental design (FFED)

The statistical optimization of six parameters (independent variables), including the time of interaction of AB113 dye solution (adsorbate) with NIFGS dosage and particle size (adsorbent), temperature and time of interaction process between adsorbent and adsorbate, initial dye concentration and pH of the solution and their effects on adsorption process of dependent variable, namely qe (adsorption equilibrium) using FFED resulted in arriving at a quadratic equation as shown below (Eq. 8)

$${\text{Adsorption}} = 38.2 + 65.3*A + 23.5*B + 143.3*C - 25.4*D - 45.9*E - \, 24.0*F + 2.7*AB + 67.9*AC + 30.7*BC23.0*A^{2} + 1.9*B^{2} + 6.6*C^{2} + 0.8*D^{2} + 49.2*E^{2} - 40.6*F^{2} .$$
(8)

The above quadratic model is useful in predicting the maximum adsorption capacity as also gives idea about the interaction between independent variables and their effect on adsorption process through analysis of variance (ANOVA). The calculations of ANOVA are characterized by computing a number of means and variances, dividing two variances and comparing the ratio to a value to determine statistical significance. The values presented in Table 8 obtained from the quadratic regression analysis clearly show the significance of individual and combined effects of independent variable(s). The values obtained through statistical optimization are 661.50 mg g−1 (maximum adsorption), 0.6 g L−1 and 321 µm (adsorbent dosage and particle size), 199 min and 52 °C (time and temperature) with orbital shaking of 165 rpm. The effects of two independent variables together on adsorption (the dependent variable) are graphically presented in the contour and surface plots (Fig. 11a–d).

Table 8 ANOVA for fractional factorial experimental design
Full size table
Fig. 11
figure 11

2D-contour plot and 3D-surface plot showing the variation of adsorption capacity with a time versus concentration, b temperature versus pH, c time versus adsorbent dosage and d concentration versus particle size

Full size image

Application of proposed method to textile industrial effluent

A simple procedure was developed to compare the remediation process for AB113 dye in water as also in textile industrial effluent, and these are explained elsewhere (Dhaif-Allah et al. 2019). This procedure was also adopted using NIFGS as adsorbent. Recovery of the dye and allied substances to the extent of 75%, 90%, 93% and 95% after 15, 30, 45 and 60 min, respectively, was obtained. This observation is in line with the kinetic results, where the solute gets adsorbed onto the surface quickly forming a film. Later on, the adsorption gets retarded due to the formation of film thereby causing change in absorption rates (Fig. 12). Scaling up of the experiment was done by using 10 g, 20 g and 50 g of NIFGS and using 1, 2 and 5 L of AB113 dye dissolved in TIE. Results did not exceed in all cases ± 2% error. The scale up experimental data yielded promising and reliable results about the process which could be extended to a higher scale to operate under industrial environment.

Fig. 12
figure 12

Color of the solutions before and after adsorption: (1) distilled water, (2) AB113 in distilled water, (3) TIE, (4) AB113 in TIE, (5) filtrate after adsorption of dye on NIFGS after 15 min, (6) 30 min, (7) 45 min, (8) 60 min and (9) filtrate of NIFGS in distilled water

Full size image

Regeneration of the adsorbent and cost analysis

Dye-adsorbed NIFGS can be regenerated for its reuse along with the recovery of the adsorbed NIFGS. But the proposition may not prove economical because the process and solvents cost will be much higher when compared to the recovered adsorbent cost (< 1 US$ for 50 Kg of NIFGS). In addition, the enhancement of E-factor (Sheldon 1992) is not desirable since it will add to the unprecedented load of environmental toxicants. But in our laboratory, work is in progress to use dye adsorbed nutraceutical industrial spent as filler/reinforcing material and encouraging results have come out and a part of it have been published elsewhere (Taqui et al. 2017, 2019).

Conclusion

The results of research have conclusively proven that use of NIS for the adsorption and remediation of toxic dyes from textile industrial effluent is not only a successful process but also has significant economic payoffs. Use of NIFGS as an adsorbent is an eco-friendly and potentially a low-cost process for removing toxic dye from aqueous media. Optimization of six physicochemical parameters, namely pH of the solution, initial dye concentration, adsorbent dose, contact time of the adsorbent and the adsorbate and temperature and nine isotherm models studied deduces an experimental value of maximum adsorption qe= 91.00 mg g−1, which is nearest obtained by the Brouers–Sotolongo isotherm model (Qm = 108.00 mg g−1) with the correlation coefficient (R2) of 0.97. FFED and ANOVA along with statistically developed model for adsorption of AB113 dye onto NIFGS predicted a maximum adsorption of 661.5 mg g−1. The p value < 0.001 surmises that pH and time of contact between the adsorbent and the adsorbate and temperature play important role in enhancing the efficiency of adsorption of the toxic dye on NIFGS. The AB113 dye adsorption on to NIFGS is not only endothermic but also almost spontaneous. It fits well with pseudo-second-order kinetic model; film formed significantly affects intra-particular diffusion. The physical nature of the process is evident by low \(\Delta H\) value. The adsorption of AB113 dye onto NIFGS was further confirmed by SEM images and FTIR spectra.

Commercialization and utilization of dye-adsorbed spent as filler/reinforcement material(s) in the fabrication of low-cost thermoplastics and thermosets will create more jobs and ecologically alleviate NIS disposal problems in landfills. This clean, cheap and efficient technology for the disposal of spent material from nutraceutical industries will definitely cater to the requirement of sustainability; economic gains, environmental concern and social obligation.