Introduction

The hard rocks terrains such as granites are usually devoid of primary porosity. Secondary porosity was developed due to weathering and fracturing of the hard rock and forms a good aquifer zone for groundwater occurrence and movement. The occurrence and movement of groundwater in such formation mainly depend on factors like saturated thickness of the weathered zone, its intensity, areal extend, and interconnection of joints and fractures. In hard rock terrain, the yields of bore wells decrease with depth (Landers and Turk 1973). This is mainly due to a decrease in the degree of weathering and fracturing with depth. Thus, most of the groundwater circulation restricts to a shallow depth in the weathered and fractured zone. The optimal depth of highest yield of bore wells in granitic terrain ranges from 20 to 30 m (Landers and Turk 1973). Furthermore, it has been recognized that there is considerable variation in the yield of bore wells within a short distance (Ballukraya et al. 1989; Singh et al. 1999; Uhl and Sharma 1978).

Estimation of aquifer characteristics and its parameters are very vital in groundwater resources studies. The hydraulic conductivity of an aquifer quantifies the ease through which water circulates in the intergranular pores and fractured formation (Szabó 2015). In hydrogeological studies, it is one of the most vital petro-physical properties of rocks or formations that can be measured in the laboratory or by performing aquifer tests in the field (Idrysy and De Smedt 2007; Ross et al. 2007; Odong 2013). Aquifer parameters can be used in groundwater modeling studies and in calculating water budgeting for future groundwater prospects. Many other researchers used geophysical methods (Vertical Electrical Soundings) and few pumping test results to estimates the aquifer properties at unknown sites where pumping test was not performed (Kosinki and Kelly 1981; Frohlich and Kelly 1985; Niwas and Singhal 1981; Huntley 1986; Susan and Rubin 2002; de Lima and Niwas 2000; Dhakate and Singh 2005).

The main objectives of this study are to assess the groundwater potential in the granitic area by estimation of the aquifer parameter which is very essential in groundwater development and management studies. Pumping tests, with short duration, have been carried out in different geomorphologic units in granitic terrain of Wailpally watershed, Nalgonda District, Southern India. The interpretation of test data has been performed using Theis, Jacob, Hantush, and numerical method by considering the limited extent of the aquifer and realistic field condition. The radius of influence of each pumping test well was calculated to know the extent of the effect on the vicinity of the pumping well. Similarly, the in situ discharge measurements of different bore wells were carried out in the area and compared with the radius of influence of pumping well. The comparison between the radius of influence of pumping well and discharge measurement will help in locating the potential groundwater zone for future groundwater development and management studies.

Study area

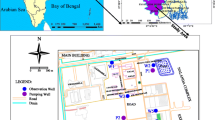
The study area Wailpally watershed lies between 17° 2′ to 17° 09′ N latitude and 78° 48′ to 79° E longitude in Nalgonda district, Telangana State, India (Fig. 1). The entire study area is occupied by the granite and gneissic rock type of Archaean age. The western part of the study area is covered by hilly terrain. Common soil types are namely red soil, loamy soils, sandy soil, and few patches of black soils were observed in the study area (Firozuddin and Rao 1991). Red and black soils are resultant weathering of pink and gray granites. The drainage patterns are dendritic to sub-dendritic in nature and climatic conditions are arid to semiarid.

Fig. 1
figure 1

Key map showing geology of the area

Full size image

Geological setting

The area is mainly occupied by granites and gneisses rock types of Archaean age. The nature of granites is mostly pink and gray color and textures of pink granites are medium to coarse-grained, while gray granites are fine-grained in texture. Pink granites are found to be more favorable for groundwater prospects than gray granite due to its interrelation in their grain size and more weathering nature, whereas in gray granite, groundwater prospects are less due to its fine-grained texture and less resistance to weathering. Pink granite is predominantly distributed throughout the area, while gray granite occupies specific areas of Puttapaka, Jangoan, and Anthampet. The dolerite dyke intrusions are trending mainly east–west and northeast–southwest. The recent alluviums were found along the stream course. At many places, these dykes control the occurrence and movement of groundwater. The weathered zone thickness varies from place to place in the study area. The geology map of the study area is shown along with key map in Fig. 1 (GSI 1989).

Geomorphologic units

The landforms identified from the satellite imagery have been visually interpreted using False Color Composites of Thematic Maps of the study area (APSRAC 1992). These maps are helpful in identifying favorable groundwater zones in the area. Various geomorphologic units that are identified are described as follows and shown in Fig. 2.

Fig. 2
figure 2

Geomorphologic map showing pumping test locations. (DH—Denudational Hills, RH—Rocky Hills, VF—Valley Fills, PPM—Pediplain with moderate weathering, PPS—Pediplain with shallow weathering, BPPS—Buried pediplain with shallow weathering, BPPM—Buried pediplain with moderate weathering, PPMA—Peniplain with moderate weathering, PPSA—Peniplain with shallow weathering and P—Rocky pediments)

Full size image

Pediplain with moderate weathering (PPM): These features are seen nearly all over the area. Groundwater prospects are moderate to good but very good along fractures/lineaments.

Buried Pediplain with moderate weathering (BPPM): These features are seen in the northern part and central part of the area. The groundwater prospects are moderate to good.

Buried pediplain with shallow weathering (BPPS): These features are observed in the central part of the area in patches. The groundwater prospects are poor to moderate, but moderate yield is expected along fracture/lineaments.

Pediplain with shallow weathering (PPS): These features are observed in the central part of the area. The groundwater prospects are poor to moderate. Moderate yield is expected along fracture/lineaments.

Peniplain with shallow weathering (PPSA): This feature observed in the northern part of the area in patches. This feature is having almost a plain area. The groundwater prospects are moderate to good.

Peniplain with moderate weathering (PPMA): These features are observed in patches everywhere in the area. The groundwater prospects are moderate to good.

Denudational Hills (DH), Rocky Hills (RH), and Rocky pediments (P): The denudational hills features are observed in the western part of the area, whereas rocky pediments observed in the northern and southern parts. The groundwater prospects are very poor.

Valley fills (VF): These features are observed in the southwestern part of the area and consist of cobbles, pebbles, sand, and silt. The groundwater prospects are good to very good. These features consist of thick alluvium and weathering cover.

Lineament studies: Lineaments were mainly originated due to tectonic origin; they are narrow to relatively straight linear features which can be discernible in satellite imagery due to their tonal differences as compared to other features. A lineament may correspond to fractures, faults, and/or joint. They are long and linear features and may be easily represented on satellite images as a straight stream course, alignment of vegetation, or any topographic features as aligned ridges. The observed lineaments may be the result of faulting and fracturing and therefore, these are inferred as increased porosity and permeability and significant for groundwater prospecting in hard rock areas. False Color Composite of Thematic Maps (TM Data) was used to identify the lineaments by visual interpretation of satellite imagery (APSRAC 1992). Minor and major lineaments were identified from the satellite imagery. The lineaments are of varying dimensions and orientations (Fig. 2).

Pumping Tests

In order to assess the aquifer parameters, namely transmissivity (T) and storativity (S), 20 pumping tests have been carried out in the watershed (Fig. 2). When the well pumped, the groundwater flow from the pumping well becomes symmetrical in all directions and the groundwater flow can be described by the equation as follows:

$$ \frac{{\partial^{2} s}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial s}{\partial r} = \frac{S}{T}\frac{\partial s}{\partial t}, $$
(1)

where s is drawdown at distance r and t is time. The above equation is used for unsteady-state groundwater flow in a homogeneous, isotropic, and confined aquifer and the boundary conditions can be described as follows:

Initial drawdown in the well is zero,

$$ s(0) = 0 $$
(2)

Initial drawdown in the aquifer is zero,

$$ s(r,0) = 0 $$
(3)

At any time (t), the drawdown in the aquifer is equal to that in the well,

$$ s(r_{w} ,t) = s_{w} (t) $$
(4)

At large distance, the drawdown is zero at time (t)

$$ s(\infty ,t) = 0. $$
(5)

The discharge rate of the well is equal to the sum of the rate of flow of water into the well. If aquifers are of low permeable nature, then the rate of decrease in the volume of water in the well should be considered significantly (Bear 1979).

$$ 2\pi r_{w} T\frac{{\partial s(r_{w} ,t)}}{\partial r} - r_{c}^{2} \pi \frac{{\partial s_{w} (t)}}{\partial t} = - Q\quad t > 0, $$
(6)

where sw is drawdown (meters) in the well at time t (minutes); rw is the effective radius (meters) of the well screen; rc is the radius (meters) of well casing and Q is a constant discharge rate (m3/day) during the test.

By using Laplace transform, the solution for Eq. (6) can be written as (Bear, 1979).

$$ s = \frac{Q}{4\pi T}F(u,\alpha ,\beta ), $$
(7)

where F(u,α,β) is well function.

$$ u = \frac{{r^{2} S}}{4Tt},\alpha = \frac{{r_{w}^{2} S}}{{r_{c}^{2} }}\;{\text{and}}\;\beta = \frac{r}{{r_{w} }}. $$
(8)

The values of well function for various values of u are given by (Papadopulos and Cooper 1967). They have further described the method to calculate T and S from the pumping test data.

Interpretation of test data

Twenty pumping tests were carried out in the study area. Interpretation of test data to estimate aquifer parameters was carried out by different methods, viz., Theis, Jacob, Hantush, and numerical method. For estimation of aquifer parameters by Theis, Jacob, and Hantush method Aquifer Test Version 4.0 software was used. The interpreted pumping test results by Theis and Hantush method for PT-3 and PT-13 in PPM and PPS geomorphologic units are shown (Fig. 3a, b). The limitations and constraints of each method for interpretation of test data are described below.

Fig. 3
figure 3

Interpreted time-drawdown/recovery plot by Theis and Hantush methods for test in pediplain with moderate weathering (PPM) and pediplain with shallow weathering (PPS) geomorphologic units

Full size image

Theis method of interpretation

The equations for unsteady-state groundwater flow in a confined aquifer with specific boundary conditions and assumptions were made for the solution (Theis 1935). The permeable layer is considered bounded above and below by an impermeable layer, i.e., the aquifer is isotropic and homogeneous. However, it is considered that all layers are of infinite extending, homogeneous in nature, and have a constant thickness. The discharge rate was considered to be constant throughout the pumping and the well is screened over the whole thickness of the permeable layer. Storage can be neglected for a very small diameter well. For poor permeability and high discharge rate during the pumping phase, the well storage affects, the total discharge rate and aquifer discharge toward the well also varies during the pumping phase (Singh 2000). Theis method can be used to estimate aquifer parameters, in the case of aquifer having higher permeability and contribution from the aquifer and well storage effect becomes insignificant (Theis 1935). Therefore, this method of interpretation was not accurate having a variable discharge rate and the interpretation gives ambiguous results.

Jacob method of interpretation

The simplified method proposed by Jacob (1963) is based on Theis assumptions, and hence, this method also does not consider variation in the aquifer discharge rate. In Jacob method, the fact that impermeable layers bound the permeable layer is the most stringent. No such situation is encountered in nature and users of the model should be aware of the implications. Flow from the bounding layers is totally ignored. Water that leaks from these layers will result in smaller drawdowns than in the case of a confined aquifer. Interpretation with the model of Theis will lead to a derived horizontal conductivity for the pumped permeable layer that is too high. If this conductivity is used for calculating travel times for solute transport, velocities will be too high and tracer breakthrough will be calculated too early. The amount of water leaking from the surrounding layers into the pumped layer can be quite large and so will be the reduction of the drawdown with respect to the Theis model drawdowns at the same locations. This effect is illustrated by the results of Wenzel (1942), one of the first to apply the model of Theis. Wenzel (1942) found the results strongly depending on the observation well. Using an observation well at a large distance from the pumping well will lead to a larger hydraulic conductivity derived with the Theis method than using drawdowns from an observation well close to the pumping well. Therefore, a larger amount of leakage between observation and pumping wells is neglected for an observation well positioned farther from the pumping well. Therefore, Jacob’s method is also not suitable in our case study.

Hantush method of interpretation

Hantush model is an extension of the theory of the radial flow toward a pumping well with a complete screen in a semi-confined aquifer and with a constant discharge rate. Storage decreases in the bounded semi-permeable layers are accounted for in the model of (Hantush 1960). To solve the partial differential flow equation, a constant hydraulic head is assumed at the top of the superjacent layer and at the base of the subjacent layer. One of these boundaries can also be treated as impermeable. In reality, however, these constant head boundaries will not be encountered in most circumstances in nature, although the model of Hantush features a more realistic approach to the groundwater flow. Similarly, the method described by Hantush (1960) also required the discharge rate to be constant, and hence, it is not suitable for tests conducted in our study area.

Rushton and Redshaw (numerical method) of interpretation

These different analytical solutions of the partial differential groundwater flow equation thus have one common disadvantage, they tend to underestimate the flow from adjacent semi-permeable layers and therefore overestimate/underestimate the horizontal conductivity of the pumped permeable layer. This overestimation/underestimation enlarges with the well distance, because the amount of ignored or overestimated/underestimated leakage becomes larger. Analytical models are very rigid in boundary conditions and strict configurations of semi-permeable and impermeable layers are required, although analytical models have struck root in literature and are successfully used to provide a solution in pumping test interpretation. Velocities calculated with the horizontal conductivities obtained by fitting inappropriate analytical models to observed drawdown are often too high.

Therefore, models that better approximate real flow conditions have to be applied. Numerical models provide the opportunity to set up a generalized interpretation method for pumping tests. The model used for this research does not only give the optimal values for the hydraulic parameters but in addition provides information about the accuracy of their derivation; therefore, numerical method of interpretation is generally used for varying discharge rate and boundary condition.

Further, in hard rock terrain where aquifers are of poor permeability, the aquifer response during the pumping period is almost negligible, and hence, it was suggested to include the recovery phase data to evaluate the aquifer parameters (Singh and Gupta 1986). Also, in the hard rock most of the shallow aquifers are of small saturated thickness and during the pumping test, there may be significant variation in the saturated the thickness of the aquifer, particularly in the vicinity of the pumping well.

In order to consider various boundary conditions that occur in the study area, described finite difference method (Rushton and Redshaw 1979) has been considered to interpret the pumping test data. The method involves solving the groundwater flow equation (1) using the finite difference method. The method can also be employed to take into account a variety of other boundary conditions, which are common in the field. The method requires the discretization of the aquifer and the test duration. The radial distance from the center of the pumping well is divided into increasingly discrete intervals (∆a = log r).

The boundary condition at the well (the discharge) and at the boundary is also prescribed in similar terms as expressed by Eqs. 2 to 6. Thus, finite difference expression is written as

$$ \frac{{mk_{r} }}{{\Delta a^{2} }}(s_{n + 1} - 2s_{n} + s_{n + 1} )_{t + \Delta t} = S\frac{{r_{n}^{2} }}{\Delta t}(s_{n,t + \Delta t} - s_{n,t} ) + Q_{{t + \frac{1\Delta t}{2}}} r^{2}, $$
(9)

where sn is the drawdown at the nth node of radial distance r and time t, kr is the hydraulic conductivity and m is the saturated thickness of the aquifer. The above equation, when written at various nodes of the model, forms simultaneous equations, which may be solved for drawdown.

The well storage is considered by assuming that the aquifer extends into the region of the well. The properties of this region are considered differently so that it represents free water to well. In this model, the horizontal hydraulic resistance \( \left( {\frac{{\Delta a^{2} }}{{mk_{r} }}} \right) \) and time resistance \( \left( {\frac{\Delta t}{{Sr_{n}^{2} }}} \right) \) at the node representing well area, are suitably modified to represent free water in the well.

Initial guess values of aquifer parameters are used to calculate the time-drawdown/recovery data and matched with the observed time-drawdown/recovery data. The aquifer parameters are then varied to get a close match between the observed and calculated time-drawdown/recovery information.

The best fit of these curves gives representative aquifer parameters. The best fit of the time-drawdown/recovery plot calculated by the numerical method from two major geomorphologic units for the test No. PT-3 and PT-5 which lies in the pediplain with moderate weathering (PPM) geomorphologic unit is shown (Fig. 4a, b). Similarly, time-drawdown/recovery plots for the test No. PT-8 and PT-13, which lies in the pediplain with shallow weathering (PPS) geomorphology unit, are shown (Fig. 5a, b).

Fig. 4
figure 4

Interpreted time-drawdown/recovery plot by numerical methods for test in pediplain with moderate weathering (PPM) geomorphologic units

Full size image
Fig. 5
figure 5

Interpreted time-drawdown/recovery plot by numerical methods for test in pediplain with shallow weathering (PPS) geomorphologic units

Full size image

Assumptions are a part of all pumping test data analysis and interpretations. These are discussed earlier in the article. The interpretation of pumping test data for Theis, Jacob, and Hantush methods is carried using Aquifer Test Software Version 4.0 by matching limited time-drawdown/recovery curves on a set of master curves available, which are drawn for known aquifer parameters. When the field time-drawdown/recovery curves obtained by carrying out pumping tests on wells are superimposed on master curves, a perfect match point is not always possible. Hence, the best match which almost resembles the master curve is used for interpretation. However, by following these methods, the shortfalls of approximation can be reduced the reliability of the interpretation.

The interpretation of pumping test data by the numerical method is different. It is carried out by using a computer program. In this method, time of pumping and recovery, measured discharge, static water levels, etc. are fed to the program. In the program, initial guess or appropriate values of storativity (S) and transmissivity (T) was fed into the program before execution. After execution of the program, generates its own time-drawdown/recovery data. Initially, the time-drawdown/recovery data obtained in the field will not match completely with the time-drawdown/recovery data generated by the software by inversion of hydrogeological data. After, a few iterations are carried out by reviewing S and T values until the time-drawdown-recovery data obtained in the field match completely with the time-drawdown/recovery data generated by the program. S and T values with satisfying the field data generated by the program are taken as final values of S and T of the aquifer under consideration. Hence, in this method of interpretation the shortfall of approximations is more or less ruled out and the reliability of the interpretation increases. In view of the above discussed factor, data interpreted by using the numerical method are more reliable and closer to theoretical values. Hence, the aquifer parameters estimated by the numerical method are considered the best values and is further used for other purposes.

Result and discussion

Short duration pumping tests ranging from 45 to 80 min period of time were carried out at 20 sites in granitic terrain. The sites were chosen in various geomorphologic terrains like pediplain with moderate weathering (PPM), pediplain with shallow weathering (PPS) and buried pediplain with shallow weathering (BPPS). Location of the test sites along with geomorphologic units in the study area is shown in Fig. 2. Pumping tests were carried out at twelve sites in pediplain with moderate weathering (PPM), six sites in pediplain with shallow weathering (PPS), and two sites in buried pediplain with shallow weathering (BPPS). The data recorded during pumping tests at all sites are shown in Table 1. Transmissivities were estimated by Theis, Jacob, Hantush, and Rushton and Redshaw methods for aquifers in all the sites where pumping tests were carried out and are given in Table 2.

Table 1 Summary of the pumping test
Full size table
Table 2 Transmissivity (T), storativity (S), and radius of influence (R) of aquifers as determined by various methods
Full size table

Transmissivity estimated by Theis, Jacob, and Hantush methods does not take into consideration of aquifer thickness, recharge areas, discharge areas, the radius of influence, etc. Hence, the computed time-drawdown/recovery will not match with the field time-drawdown/recovery curve. Hence, the reliabilities for estimation of T values by these methods are not up to the mark. However, the package used by Rushton and Redshaw method the field conditions discussed above is considered while estimating the T and S values. Hence, compared to the results obtained from Theis, Jacob, and Hantush method, the T and S values estimated by Rushton and Redshaw method are more reliable. The above result tells the anisotropic nature of the aquifer in various geomorphologic units.

The variations in T values estimated by different methods in different geomorphologic units are presented in Table 3. PPM geomorphologic unit consists of 8–20 m thick weathered material with red soil cover, which has very high porosity and permeability. The groundwater prospects in these units are moderate to good; very good prospects are found along fractures/lineaments (Dhakate et al. 2008). High values of T in PPM geomorphologic unit range from 3.85 to 436 m2/day; 3.90 to 436 m2/day; 2.9 to 414 m2/day; and 3 to 455 m2/day estimated by Theis, Jacob, Hantush, and Rushton and Redshaw method in this unit are due to the groundwater contributing from a fractured zone which is well connected to these wells (Table 3). In PPS geomorphologic unit, T ranges from 3.77 to 718 m2/day, 3.73 to 769 m2/day, 2.56 to 755 m2/day, and 3 to 700 m2/day estimated by Theis, Jacob, Hantush, and Rushton and Redshaw method, respectively (Table 3). This geomorphologic unit consists of 0–8 m thick weathered material with black soil, which has very high porosity but less permeability, the groundwater prospects are poor to moderate, but the moderate yield is found along fracture/lineaments (Dhakate et al. 2008). Similarly, in the case of the BPPS unit, T ranges from 16 to 160 m2/day, 17.3 to 152 m2/day, 19.3 to 118 m2/day, and 17.4 to 144.5 m2/day estimated by Theis, Jacob, Hantush, and Rushton and Redshaw method, respectively. The weathered thickness in this unit is 0–8 m thick with black soil. The groundwater prospects are poor to moderate, but moderate groundwater prospects are expected along fracture/lineaments (Dhakate et al. 2008). The low and high T values in PPM unit are 2.9 m2/day and 455 m2/day in PT-19 and PT-5 estimated by Hantush, and Rushton and Redshaw methods, in the PPS unit the low and high values of T is 2.56 m2/day and 769 m2/day in PT-20 and PT-13 estimated by Hantush and Jacob method, while in the BPPS unit the low and high values are 16 m2/day and 160 m2/day estimated by Theis method (Table 2).

Table 3 Variation of transmissivity estimated by different methods and radius of influence in different geomorphologic units
Full size table

A qualitative geomorphologic trend can be visualized in the study area. In the PPM geomorphologic unit, the T values are estimated by Rushton and Redshaw are high, they range in two groups, (a) in this group the T ranges from 3 to 54 m2/day and (b) in this group the T ranges from 138 to 455 m2/day. The radius of influence for the group (a) is 9.75–1391 m and (b) it is 329.87–798.89 m (Table 2). This behavior qualitatively tells that as the radius of influence increases the T also increases and vice versa. Similarly, in PPS geomorphologic unit for low ranges of T is 2.56–769 m2/day, the radius of influence is 8–698 m (Table 2). Hence, the above-mentioned relation between T and Radius of influence holds good. A qualitative practice is visualized in the behavior of T and radius of influence in pediplain in moderate weathering and pediplain with shallow weathering as explained above.

Another interesting phenomenon is observed in the relation between thickness of the weathered zone and T and radius of influence regime. As explained above in the PPM zone the T ranges are 3–54 m2/day and 138–455 m2/day. The corresponding radius of influence ranges is 9.75–1391 m and 329.87–798.89 m. In this geomorphologic unit, the weathering ranges from 8 to 20 m. On the contrary in the PPS unit, the T ranges in general are low and high 2.56–769 m2/day, and the radius of influence ranges is also low to high 8–698 m. From the above analysis, it is clear that as the thickness of weathering increases the (T) and radius of influence also increases and vice versa. Therefore, the areas which are having PPM unit are good for groundwater exploration as compared to PPS and BPPS units.

The radius of influence of each pumping test well was calculated after taking into account the values of T and S estimated by Rushton and Redshaw (1979) calculated using the equation (Bear 1979). The equation is as follows:

$$ R(t) = \sqrt {1.5\left( {{\raise0.7ex\hbox{${Tt}$} \!\mathord{\left/ {\vphantom {{Tt} S}}\right.\kern-0pt} \!\lower0.7ex\hbox{$S$}}} \right)}, $$
(10)

where R(t) = Radius of Influence in meters; T = Transmissivity; t = Time of pumping in days; S = Storativity.

The variation in radius of influence estimated by the above equation of each well is given in Table 2 and shown in Fig. 6. This figure reflects the behavior of the radius of influence of each pumping test well. To interpret the radius of influence in the entire study area and to demarcate the potential and non-potential areas in a better way, the contour pattern of these estimated values is drawn as shown in Fig. 7.

Fig. 6
figure 6

Map showing the radius of influence (meters) of each pumping test wells

Full size image
Fig. 7
figure 7

Map showing the contour pattern of radius of influence (meters) of each pumping test well

Full size image

The radius of influence ranges from 9.75 to 1391 m, 8.0 to 698.09 m, and 380.78 to 433.76 m in the PPM, PPS and BPPS geomorphologic units, respectively (Table 2). As mentioned earlier in PPM unit, the weathering thickness varies from 8 to 20 m, whereas in PPS and BPPS unit it varies from 0 to 8 m. Transmissivity values estimated by Rushton and Redshaw method in PPM units is higher than compared with PPS and BPPS units. Similarly, the radius of influence is also high in PPM units as compared with PSS and BPPS units. Therefore, the areas which are having PPM units are good for groundwater exploration as compared to PPS and BPPS units.

Similarly, discharges of eighty different wells located in major geomorphology units were measured at different intervals of time. The contour pattern of measured discharge (m3/day) is shown in Fig. 8. After comparing Figs. 7 and 8, as the radius of influence increases, the measured discharge also increases.

Fig. 8
figure 8

Map showing the contour pattern with interval (100 m3/day) of measured discharge (m3/day) from different wells

Full size image

A comparative analysis of contour patterns of T with geology and structures shown in figure reveals an interesting phenomenon. As can be seen from Fig. 9 that a higher variation of transmissivity values was observed in only two vicinities such as Wacha Tanda and Ghutuppal. These regions are characterized by a network of lineaments trending east–west and a major lineament trending NW–SE. These observations, when compared with the discharge contour shown in Fig. 8, reflect the influence of structures on T values. In Fig. 9, the T values increase continuously from the weathered zone toward the north from 100 to 400 m2/day. Transmissivity values also increase from 400 to 700 m2/day as proceed from south of Ghutuppal village. Hence, the groundwater potential is controlled by structures trending E–W and NW–SE in the study area, reflected in the prominent regimes of T and discharge. The lineaments shown in Fig. 8 have created a fractured sub-surface in the regions of high T and discharge. This is due to the movement of groundwater into the aquifer system from the surroundings areas, which makes the discharge rate high within its radius of influence and hence increases the potentiality of wells within its radius. The variation of (T) values from these three geomorphologic units is presented in a graphical form shown in Fig. 10. Thus, estimating aquifer parameters is vital for groundwater development and management studies.

Fig. 9
figure 9

Variation of transmissivity (m2/day) values with geology and lineaments

Full size image
Fig. 10
figure 10

Variation of transmissivity (m2/day) values in pediplain with moderate weathering (PPM), pediplain with shallow weathering (PSS) and buried pediplain with shallow weathering (BPPS) geomorphologic units

Full size image

Conclusions

Transmissivity (T) and storativity (S) have been estimated for the granitic aquifers of the Wailpally watershed area with the help of 20 pump tests conducted in shallow to deep boreholes in different geomorphologic units. The pumping test data have been interpreted with Theis, Jacob, Hantush, and Rushton and Redshaw methods for estimation of these parameters. Transmissivity (T) values estimated from all four methods for individual test sites are comparable. Transmissivity (T) values estimated by numerical method (Rushton and Redshaw) range from 3 to 455 m2/day in pediplain with moderate weathering (PPM) geomorphologic units, while it ranges from 3 to 700 m2/day in pediplain with shallow weathering (PPS) geomorphologic units. In buried Pediplain with shallow weathering, it ranges from 17 to 148 m2/day. The radius of influence varies from 9.75 to 1394 m, 8.0 to 698.09 m, and 380.78 to 433.76 m in the PPM, PPS, and BPPS units, respectively. The measured discharge of different wells varies from 28 to 659 m3/day. The large radius of influence and high discharge rate areas correspond to high groundwater potential areas. The variation in aquifer parameters in each geomorphologic unit is due to the inhomogeneous nature of the aquifer. The high transmissivity (T) values of an aquifer are due to groundwater contributed from a fracture zone to the well.