Abstract
The presence of certain toxic pollutants in water and wastewater such as chlorophenol must be eliminated, as they have negative effects on human health and the environment. Based on the state of the art, the reverse osmosis (RO) coupled with photovoltaic (PV) was chosen for wastewater treatment. The aim of this article is to evaluate the optimal operating conditions of RO-PV system that maximize chlorophenol rejection with minimal energy consumption. Two complementary approaches were followed combining physical models with statistical ones. The physical model used for the simulation is based on the equations of diffusion and matter balance. After demonstrating the reliability of this model, it was used for parametric sensitivity analysis, performing numerical experiments using a program developed under Python. The data obtained were used for operating parameters optimization, using artificial neural network method coupled with the desirability function. The results showed that the optimal values obtained, relating to feed pressure of 9.713 atm, water recovery rate of 40%, operating flow rate of 10−4 m3/s and temperature of 40 °C could remove 91% of chlorophenol with an energy consumption of 0.8 kWh/m3. This consumption allowed us to deduce that photovoltaic solar panel with a peak power of 280 Wp and a battery capacity of 9.22 kWh is sufficient to produce 1 m3/day.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Water is a vital element for human regardless of its gaseous, liquid or solid-state. It is useful for economic and social development, as well as our environmental sustainability. Around the world, water needs are growing more and more (Fiorenza et al. 2003). Many people do not have access to drinking water, especially in dry areas. It is becoming a fundamental ecological concern due to water scarcity. This shortage derives from global warming, population growth and groundwater pollution from industrial effluents or agricultural treatment. There is no fresh water supply available in sufficient quality and quantity to permit excessive use. This growing shortage and the desalination of seawater or brackish water remains an alternative to drinking water. Wastewater treatment is also an economical solution that can be used in the agricultural and industrial sectors. The latter option was put in place by the Moroccan government in order to minimize water consumption, particularly in the agricultural sector, thus using 40% of treated wastewater in agriculture and reducing 60% of pollution by 2020 (National Council of the Environment 2007). Additionally, the use of wastewater is considered as an additional resource that contributes to the protection of our environment, but this wastewater must be treated before its use, as it contains polluting substances which have negative effects on human health and the environment (Ayoub et al. 2016; El Brahmi and Abderafi 2020). Depending on the nature of the process, the composition of industrial wastewater may vary from one process to another, but it usually contains large amounts of dissolved organic matter such as benzene, toluene, ethylbenzene, xylenes, phenols and organic acids. Suspended organic mattes such as oils and greases; dissolved inorganic materials such as heavy metals, sulfates, nitrites and nitrates; and dissolved salts such as chlorides and bromides (MDDEFP 2012; Shi and Qian 2000). In water, chlorine forms toxic chlorophenols with phenol (Bliefert and Perraud 2001). These toxic pollutants must be removed by wastewater treatment (Kusic et al. 2011; España-Gamboa et al. 2012). This treatment must make it possible to extract water of quality corresponding to the different uses.
A wide variety of treatment research is available for wastewater treatment. There are studies that have demonstrated the performance of the microfiltration (MF) process for the treatment of wastewater rich in oils and greases by testing synthetic water or wastewater (Kumar and Pal 2015; Abadikhah et al. 2018). The nanofiltration (NF) process has been tested and recommended for an oil–water emulsion and for micro-pollutants (Muppalla et al. 2015). The same mixture was pretreated by electrocoagulation and followed by reverse osmosis (Silva et al. 2015). This process has proven reliable for removing chemical oxygen demand (COD), total dissolved solids turbidity, electrolytic conductivity and aluminum ions. Hafez et al. (2007) use NF followed by RO membrane separation technology for the treatment of synthetic solutions. They found that the NF membrane removes about 30% of the divalent and trivalent ions, while the RO membrane allows the separation of 99% of sulfate ions, 96% iron, 93% bicarbonate, 90% sodium ions, magnesium and sulfide, 86% potassium, 73% phosphate and 25% calcium ions. Recently, the RO process has been used for a wastewater treatment plant and has eliminated various contaminants such as caffeine, theobromine, theophylline, amoxicillin and penicillin G (Lopera et al. 2019). Different studies have shown the use of the RO for the separation of chlorophenol from wastewater (Al-Obaidi and Mujtaba 2016; Al-Obaidi et al. 2018a, b). Furthermore, this technology has been shown to be very promising for the removal of other hazardous industrial effluents, such as N-nitrosamine compounds and especially N-nitrosodimethylamine (Al-Obaidi et al. 2018a, b). These various researches revealed to us that the reverse osmosis is being developed for the treatment of different types of wastewater and can be used to eliminate almost all contaminants and pollutants. In addition to its operational flexibility, the RO involves lower capital cost and overall cost compared to thermal processes (Nisana and Benzartib 2008). During the last 10 years, the cost of membranes has been reduced by almost half.
For its operation, the reverse osmosis process requires electrical energy consumption to operate the high-pressure pumps circulation and others. This consumption is estimated with an average of 4 kWh/m3 (Nisana and Benzartib 2008) and can reach 19 kWh/m3 for large industrial units (Abdelkareem et al. 2018). The cost of this energy could represent up to 50% of the final costs of the water-based product (Peñate and García-Rodríguez 2011). Despite the progress achieved in reducing energy consumption, it remains high, which is the main reason for the limited spread of technology (Fiorenza et al. 2003). The use of renewable energy is essential to improve the quantity and quality of products and reduce greenhouse gas (GHG) emissions (Mekhilef et al. 2011). Fossil resources are not a sustainable option for the future and contribute to environmental pollution (Nisana and Benzartib 2008). Renewable energy systems offer alternative solutions to reduce dependence on fossil fuels. These sources of natural energy are becoming increasingly important for the production of electricity. Among the sources of renewable energy production, solar energy transforms radiation into electricity (photovoltaic) or converts it into heat (CSP) and wind energy that transforms the kinetic energy of the wind into mechanical energy. Choosing sustainable and viable energy for reverse osmosis wastewater treatment is a crucial and profound issue to study. According to Fiorenza et al. (2003), the most promising combination with desalination processes is solar and more precisely solar photovoltaic (PV) technology. A comparison between different technologies of desalination showed that despite the low energy requirements and the high water recovery rate of PV-coupled RO, the cost of producing water is high (Ali et al. 2011). Small capacity desalination units coupled with solar or wind power, for isolated sites, have proven to be less expensive than conventional techniques (Charcosset 2009).
In this research, attention is devoted to develop a separation process that will allow the treatment of wastewater and maximize the rejection of chlorophenol, with minimal energy consumption. However, a separation technology coupled with renewable energy will be used. Parametric sensitivity study will be followed to test five operating parameters effect of the RO-PV system. The data necessary to follow this methodology will be obtained numerically using an appropriate mathematical model based on the phenomena involved in the process. The artificial neural network method will be followed to assess the importance of the parameters on the model prediction and the determination of their optimal values.
Reverse osmosis-photovoltaic system description
The reverse osmosis-photovoltaic (RO-PV) combination remains the most appropriate choice to develop for the treatment of wastewater. Due to the mastery of the two technologies involved, RO-PV is probably the most common and the most reliable system in highly sunny countries. In southern Mediterranean countries such as Morocco, the number of days of sunshine is high and different sites have a considerable solar field; more than 3000 h/year of sunshine with an irradiation of about 5 kWh/m2/day (Ben Fares and Abderafi 2018). Solar energy can therefore be considered as the most important source of renewable energy in the country. Moreover, electricity generated by renewable energy has increased fivefold over the last decade and solar energy is the most economical choice compared to geothermal wind and ocean energy (Abdelkareem et al. 2018).
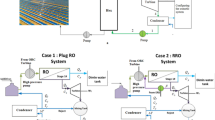
The process studied in this work is shown in Fig. 1. The RO unit is equipped with a tubular module containing a spiral wound polyamide thin-film composite membrane, then a high-pressure pump. Among the various membranes that filter the undesirable elements present in the water, one distinguishes the TFC polyamide membrane which has a good selectivity with a high rejection of solute and a good chemical, thermal and mechanical stability. It can be used for higher temperatures up to 45 °C without the risk of degradation and for pH ranges between 3 and 10 (Wang and Wang 2019).
The single-stage spiral wound configuration can be chosen because it is commonly utilized in seawater desalination and is characterized by its ease of use, in addition to its energy savings compared to two-pass RO configurations (Kim and Hong 2018). In a reverse osmosis unit, water is pumped at high pressure to the surface of the membrane causing an opposite hydrodynamic pressure greater than the osmotic pressure. The water flow rate is reversed from the concentrated side to the diluted side. Thus, the water is filtered by its passage through a semi-permeable membrane of extreme finesse from which are separated two solutions of different concentrations. The retentate is rich in concentrated brine and the permeate composed of almost pure water. The reverse osmosis unit is capable of rejecting almost all the colloidal or dissolved materials of an aqueous solution. Table 1 gives details specifications of the membrane module (Sundaramoorthy et al. 2011).
The energy necessary for the operation of the process is provided by the PV technology. The PV components used in the design and construction of this study are the polycrystalline PV modules; this choice was justified by the comparison made by Elibol et al. (2017) who studied the efficiency and performance of three types of photovoltaic solar panels. They noted that a 1 °C increase in ambient air temperature increased the efficiency of amorphous crystalline and polycrystalline panels by 0.029% and 0.033%, respectively, and reduced the productivity of monocrystalline panels by 0.084%. The photovoltaic cell consists of a semiconductor a basic material which is generally silicon. This material allows it to function as an insulator and conductor. Silicon is the most widely used material and accounts for about 90% of the market (Andreani et al. 2019) while cells using cadmuim, tellurium and indium copper diselenide (Galium) are also available but under development.
In this technology, energy is converted into electricity by the transfer of electrons using photovoltaic panels. To connect the PV to the power grid, other components such as batteries, wiring, controllers and converters are needed. The batteries are used for power stability and as an energy source for lighting at night or during periods when solar energy is not sufficient to drive the RO unit. The most used type of batteries for a solar system are lead-acid. It is cheaper and used for small installations with a very short service life of 3 to 5 years and a limited number of cycles between 300 and 500 with a depth of discharge of 80% (Freitas Gomes et al. 2020). However, it is more interesting to choose, the lithium-ion type which is more expensive, but guarantees increased durability and efficiency with a depth of discharge up to 80%, of their total capacity and a large number of cycles varying between 2000 and 5000 according to certain manufacturers (Boucar and Ramchandra 2015). The charge regulators are used to protect batteries from overcharging. The direct current (DC) obtained at the output of the battery is converted into alternating current load (AC) by the inverter.
RO-PV system modeling and validation
In this section, the model used to test the effect of operating parameters on process coupling RO with PV, for wastewater treatment, is presented. The different equations needed for this model are described below. RO model is based on diffusion and material balance equations. The solution–diffusion model is used to describe the permeation process in which all the solute and solvent molecular species dissolve through the membrane materials and then diffuse inside under the action of a concentration and pressure gradient. The separation occurs when the flux of water is different from the flux of solutes. The flux of solvent and solute through the membrane is given by (Wang and Wang 2019):
where Aw(m/atm s), Bs (m/s), ∆P(x) (atm) and ∆π(x) (atm) are the solvent transport coefficient, the solute transport coefficient, the difference in pressures across the membrane and the osmotic pressure difference across the membrane at any point on the x axis, respectively; Cp (kmol/m3) and Cm (kmol/m3) are the permeate concentration and solute concentration at the membrane surface, respectively.
The difference in osmotic pressure across the membrane is given by the following relation:
where R ((atm m3)/(K kmol)) the perfect gas constant and T (K) the temperature.
The transmembrane pressure is calculated by using the following formula:
where the retentate pressure is obtained by (Sundaramoorthy et al. 2011):
with:
where L (m), module length and W (m), the width of the membrane.
By combining the three Eqs. (1), (2) and (3), the flux of solvent is obtained:
To determine the concentration of the two outputs, a mass balance is used. The water recovery rate, the rejection rate, input flow and concentration are necessary to solve the equations of flow rate, permeate and retentate concentrations. The total mass balance and partial balance in both channels can be written as follows:
where Qf, Qp and Qr are the feed flow rate, permeate flow rate and retentate flow rate, respectively; Cf, Cp and Cr (kmol/m3) are the feed, permeate and retentate concentrations, respectively.
The water recovery rate is defined by the following relation:
The two Eqs. (9) and (10) are used to calculate the concentration of the retentate along the x-axis:
where Cp is the permeate concentration
From these two parameters, the observed rejection rate can be commonly deduced by the following equation:
with Cp (0) and Cp (L) are the permeate concentrations of the inlet and outlet, given by:
The mass transfer coefficient (m/s) is calculated by using the dimensionless number such as Reynolds and Schmidt (Murzin and Salmi 2005). After some mathematical manipulation and by choosing the Schmidt correlation established by (Sundaramoorthy et al. 2011), this coefficient is calculated from:
The diffusion (Di), viscosity (μi) and density (ρi) coefficients relative to the feed and permeate, necessary for the calculation, are given by Koroneos et al. (2007):
The electrical consumption of the necessary RO unit that can be used to remove chlorophenol from wastewater and produce this quantity of treated water (Qprod) can be calculated by the following relation:
The specific energy Esp is given by (Al-Obaidi et al. 2018a, b):
where: Pf, feed pressure (bar), Y, water recovery rate and η, pump efficiency.
The peak power of the PV collectors is calculated according to the daily electricity energy requirement, \(E_{\text{eld}}\) (kWh/day) and the monthly average daily solar irradiation of the worst month \(E_{\text{sm}}\) (kWh/m2/day) (Labouret and Villoz 2008):
where \(K_{\text{v}}\) = 0.7 is the conversion factor applied to take into account the different losses (converter, batteries, pressure drops,…)
The energy capacity of the batteries, Qb, is calculated according to the daily electrical energy requirements \(E_{\text{eld}}\), the number of days of storage desired, \(N_{\text{d}}\), and a factor \(K_{\text{b}}\) that takes into account the different losses (estimated at \(K_{\text{b}}\) = 0.7) (Labouret and Villoz 2008):
The model described above was used to calculate the chlorophenol rejection and the specific energy consumption of the RO unit. The calculation was carried out using a program developed under the software Python, following the same procedure of Sundaramoorthy et al. (2011), who developed their computer program in MATLAB language. Noted that the code relating to this algorithm is not available in the literature and it is for this reason that we have resumed the validation of the model, in this work. Figure 2 shows the flowchart of the developed program that presents the basic algorithm for a single-stage reverse osmosis unit. The equations describing the separation of water and chlorophenol through a RO membrane were solved iteratively for feed rate, pressure, solute concentration, temperature and a given water recovery rate. The calculation was initialized with a permeate concentration value equal to half that of the feed. The iterative calculation is started in the case where the constraint is not satisfied; the concentration of permeate receives a new value and continues until the required specification is satisfied.
Flowchart of the basic algorithm for a single-stage reverse osmosis unit (Sundaramoorthy et al. 2011)
The operating conditions used for model validation correspond to the experiments which were carried out by Sundaramoorthy et al. (2011). These experiments were carried out with three feed flow rates (0.0002166, 0.0002330 and 0.0002583 m3/s), five feed concentrations (0.000778, 0.001556, 0.002335, 0.003891 and 0.006226 kmol/m3) and five feed pressures (5.83, 7.77, 9.71, 11.64 and 13.58 atm), for a total number of 73 experiments.
Validation of the model was performed by comparing the calculated values obtained by following the different steps of Fig. 2, to those obtained experimentally by Sundaramoorthy et al. (2011). This comparison was made based on the correlation coefficient (R2), the mean absolute error (MAE) and the root mean squared error (RMSE), for the permeate and retentate outputs concentrations (Cp and Cr), chlorophenol rejection (Rej), flow rate and retentate pressure at the membrane outlet (Qr and Pr). The MAE and RMSE are given by these equations:
where \(V_{i, \exp }\), \(V_{{i, {\text{cal}}}}\) and n are the experimental values, calculated values and number of compounds in the data set, respectively.
Table 2 summarizes the results obtained from validation of the model obtained. This table shows that in general, the predicted values were obtained with satisfactory correlation coefficients and errors. The rejection of chlorophenol shows a correlation coefficient lower than that of the permeate and retentate; but it remains acceptable, since, statistically, the correlation between the experimental and calculated value can be considered strong if it is greater than 0.5.
The validation results obtained in this work are compared to those conducted by Sundaramoorthy et al. (2011) in Table 3. This table shows slight differences in MAE (%), for Qr, Cp and Rej. However, the difference lies in the calculation of mass transfer coefficient. The latter requires physical properties such as the diffusion (Di), viscosity (μi) and density (ρi) coefficients relative to the feed and permeate, which in our case were obtained using the correlations established by Koroneos et al. (2007).
The important MAE of Cp can be attributed to the experimental error of measurement, because the concentration analysis can provide poor accuracy for low concentrations. This accuracy also depends on the reliability of the experimental method and can be affected by the uncertainties of measures. Therefore, the model developed is reliable and can be used for parametric sensitivity analysis.
Parametric sensitivity analysis method
In this work, the artificial neural network (ANN) method coupled with the desirability function was used to analyze the parametric sensitivity of five operating parameters reverse osmosis on chlorophenol rejection and energy consumption.
The parameters which were chosen to maximize chlorophenol rejection by the reverse osmosis process are the feed flow rate (Qf), the initial concentration of chlorophenol (Cf), the temperature (T), the initial pressure (Pf) and the water recovery rate (Y). The feed rate was varied from 0.00001 to 0.0001 m3/s, so as to respect the upper limit of the manufacturer’s membrane (Al-Obaidi et al. 2018a, b). The concentration of chlorophenol is very variable and depends on the type of wastewater, the range of 0.0005 and 0.007 kmol/m3 was chosen based on the concentrations of Sundaramoorthy et al. (2011). The initial pressure and the operating temperature are selected between 5–24 atm and 25–40 °C, respectively. The choice of these different intervals was made so as to respect the limits of the operating conditions of the spiral membrane considered and respect the transport parameters (Aw and Bs) (Sundaramoorthy et al. 2011). The fifth parameter is the water recovery rate which indicates the overall efficiency of the water in the system. Although this parameter is defined as the ratio between the permeate flow rate and the feed water flow rate, it can be considered as an operating parameter of RO system (Madaeni and Eslamifard 2010; Lee et al. 2014). It’s one of the most important factors affecting the whole process that must be very high. But the concentration polarization increases with the water recovery rate and deteriorates the permeate quality. This water recovery rate varies widely and is influenced by system configuration, membrane type and feed water component quality. The range of 7 to 40% was considered for the water recovery rate, following the choice of the single stage membrane (Jbari and Abderafi 2018).
The different operating parameters of the RO unit do not have the same dimensions, which makes it difficult to compare the coefficients. The transformation of real factors into coded factors (Xi) is essential, to express the concentrations of permeat and retentate according to the different variables using a homogeneous model. This codification can also increase the precision of this model and simplify the calculation procedures.
The numerical experiments were designed on the basis of the central composite design (CCD) technique with three coded levels. The factorial portion of CCD is a full-factorial design with all combinations of the fifth operating variables, at two levels attributing (+ 1) to high value and (− 1) to low one. The coded level (0) is composed of central points, which is the midpoint between the high and low levels. Table 4 shows Levels of Central Composite Design. So, the chosen CCD allows us to conduct forty-three numerical experiments with five input variables.
Subsequently, the parametric sensitivity of the unit of RO was studied by simulation using the mathematical model developed and programmed under the Python language, following the numerical experiment plan. All the operating conditions of the process were kept fixed, with the exception of feed flow rate, initial chlorophenol concentration, temperature, feed pressure and water recovery rate which were varied to test their effects on the concentrations of permeate and retentate.
Results and discussion
The results of numerical experiment obtained by following the CCD were used to develop ANN model that allows predicting permeate and retentate concentrations of reverse osmosis process to remove chlorophenol. These results of forty-three values were randomly subdivided into two groups allocating 75% of the points to perform the neural networks training and the remaining 25% of the points was used to validate the predictions of the developed neural network models. The ANN is optimized by learning to minimize the MSE error function by seeking a set of connection weights that can allow the network to produce results that are identical or possibly equal to the target values. Levenberg–Marquardt (LM), Bayesian Regulation (BR) and Scaled Conjugate Gradient (SCG) back projection algorithms were tested using five neural networks in the input layer and two neurons in the output layer, to study the performance indicators. The hyperbolic tangent sigmoid transfer function (TanSig) and linear transfer function were used as a transfer function for the hidden layer and the output layer, respectively. The number of neurons in the hidden layer was obtained by minimizing the MSE function. Figure 3 shows the variation of the MSE as a function of the number of neurons. This figure shows that the minimum value of the MSE was obtained for a number of neurons in the hidden layer equal to three both for the concentrations of the permeate and the retentate.
In this case, the optimal structure of the ANN model developed is given in Fig. 4. This figure shows that the identified neural network comprises three neurons in the hidden layer. So the best network is represented with (5-3-2) topology. The feed flow rate, feed concentration, temperature, pressure and water recovery rate were defined as input variables in the ANN, while permeate concentration and retentate concentration were assigned as two output variables.
The reliability of the ANN model developed was performed using a set of tests based on two statistical quantities such as the correlation coefficient (R2) and the mean squared error (MSE). The statistical regression results obtained for the three algorithms tested are grouped in Table 5. This table shows that the three learning algorithms tested are comparable but the best predictions of permeate and retentate concentrations have been predicted with correlations of 0.971 and 0.999, respectively. These predictions were made with very low MSE. However, the comparison made allowed us to retain the LM algorithm. It is a more stable and faster training algorithm that uses two combined minimization techniques such as gradient descent and Gauss–Newton methods (Ozonoh et al. 2020).
Table 6 shows the comparison of correlation coefficient and MSE of the two outputs (Cp and Cr) prediction for training, validation, and prediction sets of data, using the best algorithm. This comparison shows that all the correlation coefficients tend toward 1 and the MSEs tend toward zero, both for training and validation, demonstrating the accuracy of the model for the training and validation data. Note that the different data sets that were not present in the training data are used for validation, which proves the validity of the ANN model. So, the calculated values of permeate and retentate concentrations based on the (5-3-2) topology is completely in accordance with the numerical data for training, validation and all subsets.
In Figs. 5 and 6, the calculated ANN model values were compared to the experimental numerical simulation values for permeate and retentate concentrations, respectively. These two figures show that the different points follow the diagonal with correlation coefficients that tend toward 1, which indicates that the ANN model produces very satisfactory results. The performance of the model was also obtained by representing the distribution of the residues as a function of the predicted values of the permeat and retentate concentrations in Figs. 7 and 8, respectively. These two figures show that the points are randomly distributed around the zero axes, for the permeat and retentate.
For quantifying the importance of variables in artificial neural networks, the Garson methodology was chosen (Garson 1991). This method allows obtaining precisely the importance of the variables according to its comparison with other methods by Olden and Jackson, (2002). According to this algorithm, the determination of the relative importance is calculated by:
where: RIi, the relative importance of each variable and Si, the sum of the contributions of input neurons with:
where rij, the relative contribution of each input neuron; i, j, k represent the input, hidden and output layers of the network, respectively; v, the total number of nodes in the hidden layer of the network and n, the total number of input variables in the neural network.
By following these relations, the RI calculation of the five independent variables on permeate and retentate concentrations was obtained using the matrix data containing the input–output–hidden neuron connection weights of the ANN (Table 7).
The results of the calculation of the RI of the five input variables obtained are represented in Fig. 9. This figure shows the classification of the independent variables, in the order of their effect on how the neural network classifies on the output (Olden and Jackson 2002). The feed concentration has the highest relative importance value indicating an effect of 70.83% on the retentate and 46.04% on permeate. The temperature and feed rate have a greater effect on the permeate which is 37.25% and 11.20%, respectively; while on the retentate the effect of the temperature is 9.74% and the feed flow rate is 4.72%. In regard to the effect of the water recovery rate, it is more important on the retentate concentration than on the permeate concentration. On the other hand, the supply pressure has the least contribution, with value of 1.54 and 1.05%, for Cp and Cr, respectively. These results indicate that this variable does not contribute significantly to the predicted values of permeate and retentate concentrations, but it must be taken into account in the parametric sensitivity analysis, because it has a considerable impact on the RO process (Madaeni and Eslamifard 2010).
The performance of the proposed RO-PV system was evaluated under the optimal operating parameters of the reverse osmosis. These values were obtained with ANN coupled with the desirability function. The advantage of the latter is that it allows the simultaneous optimization of several response variables (Derringer and Suich 1980). It is based on the transformation of each response obtained into a value of desirability, then as a function of total desirability. This is one of the most widely used methods in the industry to provide the most desirable response values (Gadhe et al. 2013; Borbaa et al. 2018). The optimal values parameters were obtained with a desirability function that tends to 1. Table 8 presents the outcomes obtained for each input parameter. However, it can be seen that the removal of chlorophenol can be maximized for a small value of the feed flow rate and a higher temperature. Feed concentration, temperature, and water recovery rate have competitive effects that determine the rejection of chlorophenol. However, wastewater strongly loaded with chlorophenol requires a low feed pressure and a high water recovery rate, to avoid or reduce the phenomenon of clogging membranes.
By exploiting the optimal values obtained, the quantity of water produced, the chlorophenol rejection and PV power consumption are calculated. Table 9 summarizes the results obtained. The chlorophenol rejection is calculated using Eq. (13) with optimal values of permeate and retentate. Under the optimal conditions of the single-stage reverse osmosis process, a chlorophenol rejection equal to 91% can be eliminated. The optimal quantity produced of permeate was obtained equal to 1.152 m3/d, by considering 8 h of operation of the pump. Using the optimal values of the feed pressure and the water recovery rate and with Pump efficiency η equal to 85%, the daily power consumption was obtained at 0.922 kWh/d. Subsequently, the number of photovoltaic solar panels needed to power the reverse osmosis unit was determined. The average monthly solar irradiation of the Kenitra city in Morocco was obtained using the online PVGIS software of the Photovoltaic Geographical Information System. According to simulated data, the worst month reached irradiance of 140.3 kWh/m2 in November (Fig. 10), corresponding to solar irradiation of 4.7 kWh/m2/d. Then Eq. (21) was used to calculate the peak power of the PV collectors. Knowing that the peak power delivered by each polycrystalline panel marketed is 250 Wp, it is deduce that the number of panels to install is equal to 1. For energy storage the Eq. (22) was utilized to compute the energy capacity of the batteries for a storage period of 7 days. Table 9 gives the results obtained. These results show the performance of RO-PV system that can be developed under optimal operating parameters to treat wastewater.
With the same single-stage spiral wound RO process, Sundaramoorthy et al. (2011) have obtained a maximum chlorophenol rejection of 83%, for feed pressure of 13.58 atm, feed flow rate of 2.583 × 10−4m3/s, operating temperature of 31 °C and water recovery rate of 22%. These results show that the methodology followed in this work improves the experimental chlorophenol rejection of Sundaramoorthy et al. (2011) by 10%, while increasing the total water recovery by 82%. The energy consumption obtained in this work is 0.804 kWh/m3 versus 2.044 kWh/m3 according to Sundaramoorthy et al. (2011). So, for the proper functioning of the process, it is necessary to work with the optimum operating conditions.
The efficiency of the RO-PV system can only reduce energy consumption and protect the environment from the harmful effects of factories that emit CO2. Integrating PV into an RO system is always less expensive and more ecological than a conventional system and particularly if we refer to the PV-SWRO power plants which become economically feasible for a fuel energy cost of 26 $/GJ and a cost of the photovoltaic generator from 3$/Wp (Ali et al. 2011). Manolakos et al. (2008) compare the cost of two seawater desalination RO systems. This cost comparison includes both the cost of the electrical power system and the cost of the desalination system. Their results show that the cost of the PV-RO system is much lower than that of RO-Solar Rankine system. Photovoltaic technology is developing rapidly with falling prices. The lowest retail price for a crystalline silicon solar module, in 2012 it was 1.1$/Wp (0.81€/Wp) and the lowest price for the thin-film module was 0.84 $/Wp (0.62 €/Wp) (Darwish et al. 2015). These costs information are attractive and encouraging for the application of RO-PV systems to wastewater. The techno-economic analysis of the process developed in this work for wastewater treatment will be carried out in perspective.
Conclusions
In this study, an RO-PV process was chosen to treat wastewater containing chlorophenol. Parametric sensitivity analysis was followed successfully, for five factors that influence the performances of this system.
As a first step, the phenomenological model relating to the spiral wound RO process was developed and programmed in the python language. Its validation was carried out based on experimental data available in the literature. The model can be predicting all parameters with satisfactory MAE. Then, this model was exploited to analyze the parametric sensitivity by performing numerical experiments, according to the central composite factorial design. The data obtained were used to develop an ANN model. The optimal neural network configuration obtained has one hidden layer with three neurons, having five variables as input and two outputs. From the three learning algorithms tested for training, the LM was retained to predict permeate and retentate concentrations with correlations of 0.999 and very low MSE equal to 2 × 10−8. The calculation importance of the five parameters revealed that the feed concentration is the main factor affecting the ANN configuration but the effect of feed pressure can be disregarded.
In the second step, the optimization of the RO process was realized, with the ANN model coupled to the desirability function. This optimization was carried out with objective function to maximize the chlorophenol rejection in the retentate and as decision variables the feed flow rate, initial concentration of chlorophenol, temperature, feed pressure and water recovery rate. Then, the performance of the RO-PV system was tested under its optimal operating conditions. The results obtained showed that 91% of the chlorophenol can be removed by RO of single-stage configuration, using a feed flow rate equal to 10−4 m3/s, an initial concentration value of 7 × 10−3 kmol/m3, a temperature of 40 °C, an initial pressure of 9.713 atm and a water recovery rate of 40%. The evaluation of the power consumption of the RO unit allowed us to deduce that a photovoltaic solar panel with a peak power of 280 Wp and a battery capacity of 9.22 kWh is sufficient to produce 1 m3/day.
In perspective, a techno-economic analysis to assess the investment and operating cost of the RO-PV system will be studied in further related research.
Abbreviations
- A :
-
Effective area of the membrane (m2)
- A w :
-
Solvent transport coefficient (m/atm s)
- b :
-
Feed and permeate channels friction parameter (atm s/m4)
- B s :
-
Solute transport coefficient (m/s)
- C f :
-
The feed concentration (kmol/m3)
- C m :
-
The solute concentration on the membrane surface (kmol/m3)
- C p :
-
The permeate concentration (kmol/m3)
- C r :
-
The retentate concentration (kmol/m3)
- E eld :
-
The daily electricity energy requirement (kWh/d)
- E sm :
-
The monthly average daily solar irradiation of the worst month (kWh/m2/d)
- E sp :
-
The specific energy required by the high-pressure pump (kWh/m3)
- J s :
-
The solute flux through the membrane (kmol/m2 s)
- J w :
-
The permeate flux (m/s)
- k :
-
The mass transfer coefficient (m/s)
- L :
-
The length of the membrane (m)
- P s :
-
The feed pressure (atm)
- P peak :
-
The peak power of the photovoltaic collectors (kWp)
- P p :
-
The permeate pressure (atm)
- P r :
-
The retentate pressure (atm)
- Q b :
-
The energy capacity of the batteries (kWh)
- Q f :
-
The feed flow rate (m3/s)
- Q p :
-
The permeate flow rate (m3/s)
- Q r :
-
The retentate flow rate (m3/s)
- R :
-
The gas low constant ( = 0.082 atm.m3/K kmol)
- Rej:
-
The chlorophenol rejection (dimensionless)
- RI:
-
The relative importance of each variable (dimensionless)
- S i :
-
The sum of the contributions of input neurons (dimensionless)
- T :
-
Temperature (°C)
- W :
-
The membrane width (m)
- Y :
-
The water recovery rate (dimensionless)
- ∆P :
-
The difference in pressures across the membrane (atm)
- ∆π :
-
The osmotic pressure difference across the membrane (atm)
- θ :
-
Parameter in Eq. 6
- η :
-
Pump efficiency (dimensionless)
- ANN:
-
Artificial neural network
- BR:
-
Bayesian regulation
- COD:
-
Chemical oxygen demand
- CSP:
-
Concentrated solar power
- GHG:
-
Greenhouse gas
- LM:
-
Levenberg–Marquardt
- MSE:
-
Mean-squared error
- MAE:
-
The mean absolute error
- MF:
-
Microfiltration
- NF:
-
Nanofiltration
- PV:
-
Photovoltaic
- RMSE:
-
The root mean squared error
- RO:
-
Reverse osmosis
- SCG:
-
Scaled conjugate gradient
- DC:
-
Direct current
- AC:
-
Alternating current
- CCD:
-
Central composite design
- SWRO:
-
Sea water reverse osmosis
References
Abadikhah H, Zou C-N, Hao Y-Z, Wang WJ-W, Lin L, Khan SA, Xu X, Chen C-S, Agathopoulos S (2018) Application of asymmetric Si3N4 hollow fiber membrane for cross-flow microfiltration of oily waste water. J Eur Ceram Soc 38:4384–4394. https://doi.org/10.1016/j.jeurceramsoc.2018.05.035
Abdelkareem MA, Assad ME, Sayed ET, Soudan B (2018) Recent progress in 700 the use of renewable energy sources to power water desalination plants. Desalination 701:97–113. https://doi.org/10.1016/j.desal.2017.11.018
Ali MT, Fath HES, Armstrong PR (2011) A comprehensive techno-economical review of indirect solar desalination. Renew Sustain Energy Rev 15:4187–4199. https://doi.org/10.1016/j.rser.2011.05.012
Al-Obaidi MA, Mujtaba IM (2016) Steady state and dynamic modeling of spiral wound wastewater reverse osmosis process. Comput Chem Eng 90:278–299. https://doi.org/10.1016/j.compchemeng.2016.04.001
Al-Obaidi MA, Li J-P, Alsadaie S, Kara-Zaïtri C, Mujtaba IM (2018a) Modelling and optimisation of a multistage reverse osmosis processes with permeate reprocessing and recycling for the removal of N-nitrosodimethylamine from wastewater using species conserving genetic algorithms. Chem Eng J 350:824–834. https://doi.org/10.1016/j.cej.2018.06.022
Al-Obaidi MA, Kara-Zaïtri C, Mujtaba IM (2018b) Simulation and optimisation of a two-stage/two-pass reverse osmosis system for improved removal of chlorophenol from wastewater. J Water Process Eng 22:131–137. https://doi.org/10.1016/j.jwpe.2018.01.012
Andreani LC, Bozzola A, Kowalczewski P, Liscidini M, Redorici L (2019) Silicon solar cells: toward the efficiency limits. Adv Phys X 4:1548305. https://doi.org/10.1080/23746149.2018.1548305
Ayoub S, Al-Shdiefat S, Rawashdeh H, Bashabsheh I (2016) Utilization of reclaimed wastewater for olive irrigation: effect on soil properties, tree growth, yield and oil content. Agric Water Manag 176:163–169. https://doi.org/10.1016/j.agwat.2016.05.035
Ben Fares MS, Abderafi S (2018) Water consumption analysis of Moroccan concentrating solar power station. Sol Energy 72:1146–1151. https://doi.org/10.1016/j.solener.2018.06.003
Bliefert C, Perraud R (2001) Chimie de l’environnement. Air, eau, sols, déchets. De Boeck
Borbaa FH, Seiberta D, Pellenza L, Espinoza-Quiñonesb FR, Borbab CE, Módenesb AN, Bergamascoc R (2018) Desirability function applied to the optimization of the photoperoxi electrocoagulation process conditions in the treatment of tannery industrial wastewater. J Water Process Eng 23:207–216. https://doi.org/10.1016/j.jwpe.2018.04.006
Boucar D, Ramchandra P (2015) Potential of lithium-ion batteries in renewable energy. Renew Energy 76:375–380. https://doi.org/10.1016/j.renene.2014.11.058
Charcosset C (2009) A review of membrane processes and renewable energies for desalination. Desalination 245:214–231. https://doi.org/10.1016/j.desal.2008.06.020
Darwish MA, Abdulrahim HK, Hassan AS, Mabrouk AA (2015) PV and CSP solar technologies & desalination: economic analysis. Desalin Water Treat. https://doi.org/10.1080/19443994.2015.1084533
Derringer G, Suich R (1980) Simultaneous optimization of several response variables. J Qual Technol 12(4):214–219. https://doi.org/10.1080/00224065.1980.11980968
El Brahmi A, Abderafi S (2020) Hydrogen sulfide production assessment based on sewage physicochemical properties using artificial neural network. Mater Today Proc. https://doi.org/10.1016/j.matpr.2020.03.504
Elibol E, Özmen ÖT, Tutkun N, Köysal O (2017) Outdoor performance analysis of different PV panel types. Renew Sustain Energy Rev 67:651–661. https://doi.org/10.1016/j.rser.2016.09.051
España-Gamboa EI, Mijangos-Cortés JO, Hernández-Zárate G, Maldonado JAD, Alzate-Gaviria LM (2012) Methane production by treating vinasses from hydrous ethanol using a modified UASB reactor. Biotechnol Biofuels 5(1):82. https://doi.org/10.1186/1754-6834-5-82
Fiorenza G, Sharma VK, Braccio G (2003) Techno-economic evaluation of a solar powered water desalination plant. Energy Convers Manag 44(14):2217–2240. https://doi.org/10.1016/s0196-8904(02)00247-9
Freitas Gomes IS, Perez Y, Suomalainen E (2020) Coupling small batteries and PV generation: a review. Renew Sustain Energy Rev 126:109835. https://doi.org/10.1016/j.rser.2020.109835
Gadhe A, Sonawane S, Varma MN (2013) Optimization of conditions for hydrogen production from complex dairy wastewater by anaerobic sludge using desirability function approach. Int J Hydrog Energy 38:6607–6617. https://doi.org/10.1016/j.ijhydene.2013.03.078
Garson GD (1991) Interpreting neural-network connection weights. Artif Intell Expert 6:47–51
Hafez A, Khedr M, Gadallah H (2007) Wastewater treatment and water reuse of food processing industries. Part II: techno-economic study of a membrane separation technique. Desalination 214:261–272. https://doi.org/10.1016/j.desal.2006.11.010
Jbari Y, Abderafi S (2018) Optimization of off-grid photovoltaic powered reverse osmosis system using response surface methodology. In: 6th international renewable and sustainable energy conference (IRSEC). https://doi.org/10.1109/irsec.2018.8702958
Kim J, Hong S (2018) A novel single-pass reverse osmosis configuration for high-purity water production and low energy consumption in seawater desalination. Desalination 429:142–154. https://doi.org/10.1016/j.desal.2017.12.026
Koroneos C, Dompros A, Roumbas G (2007) Renewable energy driven desalination systems modelling. J Clean Prod 15:449–464. https://doi.org/10.1016/j.jclepro.2005.07.017
Kumar R, Pal P (2015) Assessing the feasibility of N and P recovery by struvite precipitation from nutrient rich wastewater: a review. Environ Sci Pollut Res 22:17453–17464. https://doi.org/10.1007/s11356-015-54502
Kusic H, Peternel I, Ukic S, Koprivanac N, Bolanca T, Papic S, Loncaric Bozic A (2011) Modeling of iron activated persulfate oxidation treating reactive azo dye in water. matrix. Chem Eng J 172:109–121. https://doi.org/10.1016/j.cej.2011.05.076
Labouret A, Villoz M (2008) Energie solaire photovoltaïque, 3rd edn. Dunod, Belin
Lee JJ, Woo YC, Kim H-S (2014) Effect of driving pressure and recovery rate on the performance of nanofiltration and reverse osmosis membranes for the treatment of the effluent from MBR. Desalin Water Treat 54(13):3589–3595. https://doi.org/10.1080/19443994.2014.923196
Lopera AE-C, Ruiz SG, Alonso JMQ (2019) Removal of emerging contaminants from wastewater using reverse osmosis for its subsequent reuse: pilot plant. J Water Process Eng 29:1–10. https://doi.org/10.1016/j.jwpe.2019.100800
Madaeni SS, Eslamifard MR (2010) Recycle unit wastewater treatment in petrochemical complex using reverse osmosis process. J Hazard Mater 174(1–3):404–409. https://doi.org/10.1016/j.jhazmat.2009.09.067
Manolakos D, Mohamed ES, Karagiannis I, Papadakis G (2008) Technical and economic comparison between PV-RO system and RO-solar rankine system. Case study: Thirasia island. Desalination 221(1–3):37–46. https://doi.org/10.1016/j.desal.2007.01.066
MDDEFP (2012) Banque de données sur la connaissance et la surveillance de la pollution atmosphérique, données préliminaires, Québec, ministère du Développement durable, de l’Environnement, de la Faune et des Parcs. Direction du suivi de l’état de l’environnement
Mekhilef S, Saidur R, Safari A (2011) A review on solar energy use in industries. Renew Sustain Energy Rev 15:1777–1790. https://doi.org/10.1016/j.rser.2010.12.018
Muppalla R, Jewrajka SK, Reddy AVR (2015) Fouling resistant nanofiltration membranes for the separation of oil–water emulsion and micropollutants from water. Sep Purif Technol 143:125–134. https://doi.org/10.1016/j.seppur.2015.01.031
Murzin D, Salmi T (2005) Catalytic kinetics, Chapter 9—mass transfer and catalytic reactions. Elsevier, Amsterdam, pp 341–418. https://doi.org/10.1016/B978-044451605-3/50009-5
National Council of the Environment, 2007. http://www.environnement.gov.ma/fr/eau?id=207
Nisana S, Benzartib N (2008) A comprehensive economic evaluation of integrated desalination systems using fossil fuelled and nuclear energies and including their environmental costs. Desalination 229:125–146. https://doi.org/10.1016/j.desal.2007.07.031
Olden JD, Jackson DA (2002) Illuminating the ‘‘black box’’: a randomization approach for understanding variable contributions in artificial neural Networks. Ecol Model 154:135–150. https://doi.org/10.1016/s0304-3800(02)00064-9
Ozonoh M, Oboirien BO, Higginson A, Daramola MO (2020) Performance evaluation of gasification system efficiency using artificial neural network. Renew Energy 145:2253–2270. https://doi.org/10.1016/j.renene.2019.07.136
Peñate B, García-Rodríguez L (2011) Energy optimization of existing SWRO (seawater reverse osmosis) plants with ERT (energy recovery turbines): technical and thermo economic assessment. Energy 36:613–626. https://doi.org/10.1016/j.energy.2010.09.056
Shi C, Qian J (2000) High performance cementing materials from industrial slags—a review. Resour Conserv Recycl 29:195–207. https://doi.org/10.1016/s0921-3449(99)00060-9
Silva JRP, Merçon F, Silva LF, Cerqueira AA, Ximango PB, Marques MRC (2015) Evaluation of electrocoagulation as pre-treatment of oil emulsions, followed by reverse osmosis. J Water Process Eng 8:126–135. https://doi.org/10.1016/j.jwpe.2015.09.009
Sundaramoorthy S, Srinivasan G, Murthy DVR (2011) An analytical model for spiral wound reverse osmosis membrane modules: part II—experimental validation. Desalination 277:257–264. https://doi.org/10.1016/j.desal.2011.04.037
Wang Y-N, Wang R (2019) Reverse osmosis membrane separation technology. Membr Sep Princ Appl. https://doi.org/10.1016/b978-0-12-812815-2.00001-6
Funding
This study was funded by Mohammadia Engineering School.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Ethical approval
All procedures followed were in accordance with the ethical standards.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Jbari, Y., Abderafi, S. Parametric study to enhance performance of wastewater treatment process, by reverse osmosis-photovoltaic system. Appl Water Sci 10, 217 (2020). https://doi.org/10.1007/s13201-020-01301-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-020-01301-4