A basic review of fuzzy logic applications in hydrology and water resources

Abstract

In recent years, fuzzy logic has emerged as a powerful technique in the analysis of hydrologic components and decision making in water resources. Problems related to hydrology often deal with imprecision and vagueness, which can be very well handled by fuzzy logic-based models. This paper reviews a variety of applications of fuzzy logic in the domain of hydrology and water resources in brief. So far in the literature, fuzzy logic-based hybrid models have been significantly applied in hydrologic studies. Furthermore, in this paper, the literature is reviewed on the basis of applications using pure fuzzy logic models and applications using hybrid-fuzzy modeling approach. This review suggests that hybrid-fuzzy modeling approach works well in many applications of hydrology when compared with pure fuzzy logic modeling.

Introduction

Fuzzy logic is a well-known soft computing tool which develops the workable algorithms by embedding structured human knowledge. It is a logical system that presents a model designed for human interpretation modes that are inexact rather than precise. The fuzzy logic system can be applied to design intelligent systems on the basis of information expressed in human language (Bai et al. 2006). Fuzzy logic is one of the forms of artificial intelligence; however, its history and uses are newer than artificial intelligence based expert systems. Fuzzy logic deals with problems that have imprecision, vagueness, approximations, uncertainty or qualitative mess or partial truth.

Fuzzy logic was introduced by Professor L. A. Zadeh, University of California at Berkeley, in the year 1965 (Zadeh 1965; Bai et al. 2006) through his paper ‘Fuzzy sets.’ His work was not recognized until Dr. E. H. Mamdani, Professor at London University, practically applied the concept of fuzzy logic to control an automatic steam engine in the year 1974 (Mamdani and Assilion 1974; Bai et al. 2006).

Since the beginning of applications of fuzzy logic in the domain of hydrology (Bogardi et al. 1983, 2004) a great sum of investigations have been undertaken, and presently, fuzzy logic has turned into a useful approach in water resources assessment and hydrologic analysis. Hydrology is often vulnerable to uncertainties caused due to lack of data, nature causes (e.g., climate) and imprecision’s in modeling. System limitations and initial conditions as well bring in uncertainty. In addition, potential pressure on the system cannot be clearly identified in many hydrologic studies. Fuzzy logic allows us to consider the handling of all such vagueness (or ambiguity) in hydrology (Bogardi et al. 2004).

In order to employ a systems approach, it is necessary to change the fundamental understanding of physical reality under consideration (Simonovic 2008). New researchers have focused on the application of fuzzy logic-based techniques for modeling vagueness within the water resource systems. So far in the literature, many research contributions have been made for dealing with the vagueness in water resources systems which include fuzziness, bias, ambiguity and deficiency of ample data (Mujumdar and Ghosh 2008).

‘Fuzzy rule-based modeling’ is an extension of the concept of fuzzy logic. The key difference in fuzzy logic and fuzzy rule-based modeling is that the former is used for systems with feedback and the latter is used for systems with no feedback process (Sugeno and Yasukawa 1993; Wang and Mendel 1992; Decampos and Moral 1993; Bogardi et al. 2004). The idea of application of FL in the modeling of the hydrologic systems is comparatively fresh and innovative (Bardossy et al. 1995).

Some of the areas of fuzzy logic application in hydrology include: fuzzy-based regression (Bardossy et al. 1990; Bardossy et al. 1991; Ozelkan and Duckstein 2000; Bogardi et al. 2004), hydrologic forecasting (Kojiri 1988; Bogardi et al. 2004), hydrologic modeling (Hundecha et al. 2001; Bogardi et al. 2004), regional water resources management (Bogardi et al. 1982; Nachtnebel et al. 1986; Bardossy et al. 1989, Bogardi et al. 2004), reservoir operation planning (Simonovic 1992; Shrestha et al. 1996; Teegavarapu and Simonovic 1999; Bogardi et al. 2004), water resources risk assessment (Feng and Luo 2011) and so on.

To increase the accuracy of fuzzy systems, various studies have been undertaken for years and the major inference is that fuzzy hybrid modeling can efficiently increase the accuracy of fuzzy system modeling. New advances have been taken place in the fields of adaptive fuzzy operators (Terzi et al. 2006), genetic fuzzy systems modeling (Guan and Aral 2005; Han et al. 2012) and wavelet–fuzzy modeling (Partal and Kisi 2007), which will be discussed in further sections of this article.

From the early application of fuzzy logic to hydrology (Bogardi et al. 1983), a large amount of research has been pursued and, at present, fuzzy logic has become a practical tool in hydrologic analysis and water resources decision making. In this paper, the main areas of applications in hydrology and water resources are highlighted.

General methodology (work-flow of fuzzy logic systems)

In order to apply FL technique to a practical application problem, the following steps are to be followed (Bai et al. 2006):

• 1. Fuzzification—this step involves the conversion of crisp data or classical data into fuzzy set data or the membership functions (MFs)

• 2. Fuzzy inference process—this process consists of combining MFs along with the fuzzy control rules to obtain the fuzzy output

• 3. Defuzzification—this process is the reverse process of fuzzification. It involves the conversion of the fuzzy output into crisp output along with associated rules (as shown in Fig. 1).

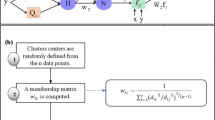
  Fig. 1

  

  Workflow of a fuzzy logic system (Bhattacharjee et al. 2018)

Machines are capable of processing crisp data such as the binary system (‘0’ or ‘1’) and can be facilitated to handle uncertain linguistic data such as ‘high’ and ‘low’ if the crisp input and output are converted to linguistic variables along with the fuzzy components. Moreover, both the crisp input and the crisp output have to be converted to fuzzy data. All of these conversions are carried out by the first step—fuzzification.

The second step is the fuzzy inference process (FIS) where membership functions (MFs) are combined with the control rules in order to derive the fuzzy control output, and the outputs are arranged into a table format called as the ‘lookup table.’ In FIS, the important is the fuzzy control rules. Those rules are as similar as that of human being’s inference and intuition to the course of action. Various methods such as mean of maximum (MOM) or center of gravity (COG) are been used to work out the related control output, and each one of the control output must be arranged into a table format called lookup table.

For a real-life application, a fuzzy control output must be chosen from the lookup table developed in the previous step based on the present input. Further, that fuzzy control output must be transformed from the linguistic variable form to the sharp or crisp variable and perform the control operator. The process is known as defuzzification or step 3.

Real-life applications are usually associated with input variables having more than one dimension. In such cases, one needs to develop the membership functions for each dimensional variable separately and the similar operation needs to be carried out if the system consists of multiple output variables.

To summarize, the fuzzy system modeling is a chain of crisp-fuzzy-crisp transformation used to derive results for an actual working system. The initial input and the final output must necessarily be crisp variables; however, the transitional stage is a fuzzy inference process, where the linguistic variables are used to derive the outputs. The motive why there is need to transform a sharp or crisp variable to a fuzzy variable is that, from the principle of fuzzy system process or a human’s inference or intuition, no absolutely crisp variable exists in our factual world.

Applications in the field of surface water hydrology

Fuzzy rule-based systems were successfully applied for drought evaluation (Pesti et al. 1996), forecasting of rainfall patterns (Abebe et al. 2000), investigation of uncertainty in modeling groundwater flow (Abebe et al. 2000), water levels control in polder areas (Lobbrecht and Solomatine 1999), modeling the dynamics of rainfall streamflow (Vernieuwe et al. 2005) and so on. Some selective applications are listed as follows:

Applications in evaporation and evapotranspiration

Fuzzy models were developed in literature for daily pan evaporation assessment from observed meteorological records. Penman equation, which is most widely used, is used to compare with the fuzzy model results. Theory of FL was successfully applied for estimating monthly pan evaporation with meteorological data as input (Atiaa and Abdul-qadir 2012). This study concluded that the approach of FL is adequate and intelligent for evaporation modeling. Fuzzy models were also developed for estimating of daily pan evaporation, and outcomes were compared with Penman method (Keskin et al. 2004). The fuzzy model proved a better agreement with observed data than the Penman method. Similarly, evapotranspiration (ET) was estimated and predicted using fuzzy inference system (FIS) by Patel and Balve (2016), and the results were compared with the FAO-56 Penman–Monteith method. FIS showed a high efficiency in predicting and estimating ET values.

Rainfall–runoff (R–R) modeling

Huge cost and labor use experienced in past for developing a water resource project request a lot of consideration in contriving exact R–R models for its fruitful execution. These models are reliant on the physiographic, climatic and biotic qualities of the watershed. These elements now and again actuate either a direct, nonlinear or profoundly complex behavior among the precipitation and runoff parameters. The unstructured idea of R–R relations has occupied the consideration of specialists toward soft computing techniques (Chandwani et al. 2015).

Hundecha et al. (2001) developed a fuzzy rule-based routine in order to simulate the generation of runoff using precipitation data. A fuzzy conceptual framework for rainfall–runoff modeling was proposed to deal with uncertainties of every element of R–R modeling (Özelkan and Duckstein 2001). The study showed that FL framework facilitates the decision maker to realize model sensitivity and uncertainty resulting from elements of R–R modeling. Further, a fuzzy rule-based system (FRBS) was developed using Takagi–Sugeno–Kang approach to forecast the definite discharge at the outlet of the catchment in which soil moisture was used as the input variable (Casper et al. 2007).

Floods and droughts

Flood disasters are among the world’s most recurrent and destructive kinds of catastrophes (World Disaster Report 1998; Jiang et al. 2009). Flood risk, disasters and hazards are the products of an interface between social and environmental processes (Parker 2000; Jiang et al. 2009). Several researchers used the fuzzy numerical technique to investigate flood forecasting and risk evaluation (Jiang et al. 2008; Mao and Wang 2002; Nayak et al. 2005; Jiang et al. 2009).

Flood disaster risk was assessed by Jiang et al. (2009) using three fuzzy-based methods such as fuzzy similarity method (FSM), simple fuzzy classification (SFC) and fuzzy comprehensive assessment (FCA). It was found that the FCA method is more reliable for the study area than the other two techniques. An attempt was made to enhance the real-time flood forecasting using a modified Takagi–Sugeno (T–S) FIS (Lohani et al. 2014). The model forecast was reasonably accurate with sufficient lead time. A flood forecasting model based on Mamdani FIS was developed by Perera and Lahat (2015) in order to assess the potential of fuzzy logic in real-time flood forecasting. A fuzzy logic-based method and geographical information system (GIS) were combined to analyze mass evacuation decision support system (Jia et al. 2016). It was helpful in illustrating the importance of evacuation maps in crisis management.

Fuzzy models were also used as updating technique in order to improve flood forecasting models (Yu and Chen 2005). A study on estimating the potential impacts of climate change on droughts was carried out by Pesti et al. (1996). In this study, fuzzy rules were applied to forecast droughts with the help of atmospheric circulation patterns.

Reservoir operation (RO)

Fuzzy rule-based models were successfully developed by the researchers in order to derive rules for operating a multipurpose reservoir (Shrestha et al. 1996) and single purpose reservoir (Panigrahi and Mujumdar 2000). Further, the complexity of fuzzy modeling for RO was reduced by reducing the fuzzy rules (Sivapragasam et al. 2008) and the results were highly encouraging the purpose of the study.

Dubrovin et al. (2002) applied the fuzzy model for real-time reservoir operation. A new methodology for fuzzy inference was developed, called as total fuzzy similarity. The study illustrated the strong mathematical background of the FIS makes the fuzzy reasoning to have a solid foundation.

Deriving stage–discharge (S–D) relationship and prediction of sediment concentrations

A fuzzy rule-based model was developed for deriving S–D-sediment concentration relationship, and the result was compared with conventional sediment rating curves and neural networks (Lohani et al. 2007). The fuzzy model showed better results and potentiality for its application in prediction of sediment concentration. Streamflow prediction was done using two FISs (Ozger 2009), and the results showed that Mamdani type of fuzzy inference modeling performs better than that of Takagi–Sugeno fuzzy inference systems for river discharge prediction.

Fuzzy models were developed as a superior alternative to traditional sediment rating curves for determining the suspended sediment concentration on a daily basis for a given river section (Kisi 2004). The study showed that fuzzy models prove their superiority in comparison with the rating curve models for the same input data. Further, Kisi et al. (2006) used the FL approach to carry out river suspended sediment modeling. They concluded that the proposed fuzzy model was site-specific and failed to simulate the effects of hysteresis.

Water quality modeling and water treatment

A fuzzy optimization model was developed for river water quality management on a seasonal basis (Mujumdar and Sasikumar 2002). The model successfully gave solutions for removal of pollutants on seasonal fraction basis. Icaga (2007) developed an index model for surface water quality classification based on the fuzzy logic concept. The study demonstrated the feasibility and practical application of the index. A two-stage fuzzy set theory was applied to river quality evaluation (Liou et al. 2003; Ip et al. 2009). A FIS was used to assess the river water quality, and the results were compared with a widely used method like water quality index (WQI) (Abdullah et al. 2008). The results clearly indicated that FIS can be successfully used to harmonize the discrepancies and the internal complexities of river water quality assessment.

Surface water quality was assessed by developing an indicator based on fuzzy logic. The results were compared with conventional WQI, in which fuzzy indicator provided better results (Oroji et al. 2017). Chang et al. (2001) studied the identification of river water quality by using three fuzzy synthetic evaluation techniques, and the outputs were compared with a conventional procedure like WQI.

Superior capabilities of the fuzzy logic concept in handling the nonlinearity, complexity and uncertainty of systems were illustrated by Bai et al. (2009) in their study of WQI based on fuzzy logic. A new WQI based on fuzzy (FWQI) was developed, and the outcomes were compared with two other indices (González et al. 2011). FWQI proved to be a potential index for a decision maker in water management. Fuzzy-based models were successfully developed for forecasting WQI in the municipal water distribution system (Patki et al. 2013), and the results of the fuzzy model were compared with adaptive neuro-fuzzy (ANFIS) models. The study revealed that fuzzy models outperformed as that of ANFIS models. Sedeño-Díaz and López-López (2016) studied reservoir water quality using a fuzzy logic model.

Surendra and Deka (2014) used Mamdani FIS for predicting water consumption using different climatic variables. Performance indicators showed the capability of fuzzy logic in predicting the water consumption in a municipal water distribution system. A novel approach based on fuzzy logic was developed for water quality assessment, especially for human drinking purposes (Gharibi et al. 2012). Fuzzy controller systems were designed and implemented by the researchers in regulating an aeration system in a water treatment plant (Fiter et al. 2005). The results illustrated that more than 10% energy savings can be achieved using fuzzy aeration control while still keeping the removal levels good. A fuzzy multi-criteria decision-making method was developed to select the optimal strategy for the rural water supply, and the results were quite promising (Minatour et al. 2015).

Downscaling of climate variables

The art of applying fuzzy rule-based techniques for downscaling of climate variables can be seen since two decades. Bardossy et al. (1995) applied the fuzzy-based method to classify the daily atmospheric circulation patterns (CPs). They stated that the fuzzy rule-based approach has high potential applications in the classification of general circulation models (GCMs). Clustering and classification of large-scale atmospheric CPs using multi-objective fuzzy technique were done by Özelkan et al. (1998). An automated objective classification of CPs for precipitation and temperature downscaling on daily basis was carried out based on optimized fuzzy rules (Bárdossy et al. 2002). The method produced physically realistic CPs. Fuzzy-based classification for downscaling was compared with two methods, analog method and statistical downscaling model (Teutschbein et al. 2011). The study demonstrated that the suitability of downscaling technique was highly variable with river basin under consideration.

Applications in the field of groundwater hydrology

Some of the important fields of fuzzy logic applications in the field of groundwater hydrology are as listed in Table 1.

Table 1 Some of the literature showing applications of fuzzy logic in the field of groundwater hydrology

Applications of hybrid-fuzzy models

Some of the selective applications of fuzzy hybrid models in water resources are listed in Table 2.

Table 2 Some of the literature of fuzzy hybrid modeling approached in water resources

Results and discussions on the literature reviewed so far

As mentioned before, fuzzy logic can very well handle the uncertainty or vagueness associated with hydrologic problems. Hence in many of the literature, fuzzy-based models have shown better performance in comparison with the conventional methods. In modeling evaporation, fuzzy modeling proved a better agreement with observed data when compared with the widely used Penman method (Atiaa and Abdul-qadir 2012; Keskin et al. 2004; Patel and Balve 2016).

Özelkan and Duckstein (2001) showed that FL framework facilitates the decision maker to realize model sensitivity and uncertainty resulting from elements of R–R modeling. In flood modeling, fuzzy models were well verified for the performance and different fuzzy models like fuzzy comprehensive assessment, simple fuzzy classification and fuzzy similarity method were compared with each other (Jiang et al. 2009).

Streamflow prediction was carried out using two fuzzy inference systems, namely Mamdani type and Takagi–Sugeno type inference systems, where the former showed better performance (Ozger 2009). Fuzzy models were proved to be outperforming in both stream water quality modeling (Chang et al. 2001) and municipal water distribution (Patki et al. 2013).

Fuzzy models were developed in different fields of groundwater hydrology like infiltration modeling, regional groundwater management, groundwater remediation, aquifer studies and groundwater pollution assessment, where fuzzy models have shown better performance.

Among the various hybrid-fuzzy models developed so far, fuzzy neural comes out to be the most widely used model in various hydrologic studies. ANFIS showed its better performing capabilities in fields like evaporation (Terzi et al. 2006); fuzzy neural network model produced good results in deriving stage–discharge relationship when compared to conventional curve fitting method (Deka and Chandramouli 2003).

Different combinations of hybrid-fuzzy modeling, like wavelet-fuzzy, wavelet-ANFIS, fuzzy-SVM, fuzzy-genetic algorithms and so on, were well experimented (as shown in Table 2), and the results show the potentiality of fuzzy systems in modeling the hydrologic components (Figs. 2, 3).

Fig. 2

Pie chart representation showing the application of hybrid-fuzzy models so far

Fig. 3

Pie chart showing representative proportions of various applications of FL in hydrology and water resources

Merits and demerits of fuzzy logic

Merits of fuzzy logic

Fuzzy logic explains schemes in expressions of a mixture of numerics and linguistics (symbolic). It has compensation over pure numerical (mathematical) methods or pure symbolic methods because frequently system information is accessible in such a mixture.

Problems for which a specific mathematically fixed account is missing or is only obtainable for very limited conditions can repeatedly be undertaken by fuzzy logic, given a fuzzy model is in attendance. Fuzzy logic at times uses only estimated data, so easy sensors can be employed. The algorithms can be explained by minute data, so minute memory is necessary.

The algorithms are frequently quite comprehensible. Fuzzy algorithms are frequently vigorous, in the logic that they are not very responsive to altering environments and mistaken or away from rules. The logic process is habitually simple, assessed to computationally exact systems, so computing influence is reserved. This is a fascinating feature, mainly in real-time systems. Fuzzy methods frequently have a shorter growth time than conventional methods.

Demerits of fuzzy logic

Fuzzy logic sums up to the function estimation in the case of crisp-input/crisp-output systems. The meaning is that in numerous cases, using fuzzy logic is just a dissimilar way of performing exclamation. In domains that have excellent mathematical imagery and solutions, the use of fuzzy logic most frequently may be rational when calculating power (i.e., time and memory) limits are too rigorous for an absolute mathematical realization.

Cautious examination of contrast examples, ‘proving’ the advantage of fuzzy logic frequently shows that they are in contrast the fuzzy technique with a very straightforward, non-optimized traditional method. Proof of individuality of fuzzy systems is not easy or unworkable in many cases because of the absence of mathematical explanations; particularly in the areas of stability of control systems which is a vital research point.

Conclusion

Fuzzy-based modeling approach is increasingly been applied in most of the fields of hydrology and water resources as it can take the uncertainties into consideration. It can also be applied effectively in cases like missing data in long-term time series, unavailability of data, prediction of time series, etc. Due to its capacity to consider the uncertainty and vagueness, it works efficiently in real-time forecasting applications. Literature shows a wide range of applicability of fuzzy logic in surface water hydrology, groundwater hydrology, irrigation technology, etc. Literature studies also show that fuzzy models are often combined with other models and the hybrid-fuzzy modeling is found to be more efficient than pure fuzzy modeling in many of the applications. In comparison with models like ANN, SVM, fuzzy models show moderate accuracy but prove a better performance when combined with other models.

Scope for future work

• Investigation of a best suitable hybrid-fuzzy model for application in hydrologic studies.

• Among the hybrid-fuzzy models, ANFIS is most widely used and accepted technique so far. It can be used for assessing the performance of hybrid-fuzzy models for the same study.

• Fuzzy logic has proven its performance in prediction studies. Hence, its predictive power can be used effectively in hydrologic time series forecasting.

• The performance evaluation of pure fuzzy modeling and hybrid-fuzzy modeling can be an important research in many hydrologic applications.

• Fuzzy logic-based models can efficiently deal with problems where data are scanty or limited.