Introduction

Synthetic precipitation time series can be used in forecasting hydrological variables, particularly in producing likely scenarios preserving interchange of dry and wet frequencies. Statistic tools such as stochastic processes and resampling methods based on estimating of a kernel density for interested data are often used in hydrological fields (Lall et al. 1996; Wang et al. 2005). Above statistic tools are generally involved in forecasting hydrometeorological data. In studies toward ensemble prediction systems, these tools are either used to provide input perturbations or to process ensembles for assessment of system performances and quality of the forecasts at deterministic or probabilistic scale. These approaches are also used in hydrological ensemble forecasting. As a history, hydrological ensemble forecasting systems (HEFSs) were initiated in the 1970s by the National Weather Service of the USA in an attempt of providing probabilistic forecasts that should take into account uncertainties of the models in forecasting streamflow (Jeong et al. 2005; Velázquez et al. 2011; Nousu et al. 2019). Otherwhere HEFSs have been increasingly developed and improved through the world to overcome flooding threats (Wetterhall et al. 2013; Schaake et al. 2010; Samaniego et al. 2019). In addition, HEFSs may constitute good tool for assessment of the climate change impacts on hydrological variables (Her et al. 2016). Hydrological ensemble forecasting consists of several forecasts of future values of a variable, namely ensemble members (Bröcker et al. 2008). Ensemble members are then used to develop some probabilistic statements of related variable such as the probability of a flooding event (fraction of the ensemble members exceeding the flooding threshold). In fact, ensemble methods are very adequate for warning droughts and floods, because of the implication of probabilistic interpretation in the forecasting approach (Samaniego et al. 2019; Roux et al. 2020). It is also used to extend the forecasting period of hydrological models (Li et al. 2019). Probabilistic approaches in hydrological forecasting are yet popular and progressively substitute deterministic approaches, particularly within worldwide renowned services acting upon flood forecasting (Cloke et al. 2009; Wetterhall et al. 2013; Jaina et al. 2018; Li et al. 2019). Such approaches have been used to simulate an ensemble of Senegal River discharge upstream the Manantali dam (Ndione et al. 2018). Besides, one can found some international organization promoting the use of ensemble forecasting systems, namely hydrological ensemble prediction experiment (HEPEX) (Schaake et al. 2006). Several studies showing performances and effectiveness of HEFSs are available in the literature. For example, Verkade et al. (2017) estimated predictive hydrological uncertainties at the Meuse and the Rhine basins by dressing deterministic forecasts using estimates of both hydrological and meteorological forecast; results show through scores that ensemble from dressing deterministic forecasts is more reliable than one produced by dressing ensemble from meteorological model. Hydrological ensemble forecasting has been used at the USA in 2017, in order to provide rationally some short- to medium-range streamflow forecast through a combination of a meteorological ensemble forcing with a distributed hydrological ensemble forecast (Siddique and Mejia 2017; Sharma 2018). Her et al. (2016) studied uncertainties inherent to an ensemble forecast from multi-GCMs (multi-model) and uncertainties from an ensemble involving estimated multi-parameters of one hydrological modeling scheme under climate change effects; they found that uncertainties from multi-GCMs may be more important in magnitude and that attention should be paid in selecting hydrological input models. Jeong et al. (2005) used both single neural network (SNN) and ensemble neural network (ENN) to improve already existing hydrological forecasting system runs with the TANK rainfall–runoff model in dry season at the Daecheong multipurpose dam in Korea. Results reported that the scheme involving the ENN improves considerably winter and springer streamflow forecasts. Pappenberger et al. (2011) reveal that the National Hydrological Service produces long-term probabilistic flood forecasting using ensemble prediction from the European Flood Alert System (EFAS) runs every week upon ten years ahead. They show that beyond the efficiency of the probabilistic forecast in comparison with classical methods, ensemble forecast is sensitive to the geographical position and to the considered catchment spread. Moreover, their analyses reveal that the use of an ensemble has enhanced the skill of the river discharges forecast system. Pagano et al. (2013) dressed raw ensemble forecasts from 120 catchments using inherent error distributions; results show that the dressing processes can enhance reliability of the raw ensemble forecast. In Addor et al. (2011), the COSMO-7 deterministic model and the probabilistic COSMO-LEPS have been coupled with the PREVAH model to help managers of the Sihl River in decision making (Addor et al. 2011).

In this paper a hydrological ensemble forecast system is tested for flow discharges of the Senegal River upper the Manantali dam. The system is composed of a rainfall ensemble provider (dressing rainfall deterministic forecast) and a hydrological model performed using above rainfall ensemble pattern. Deterministic forecast is done using classical time series analysis theories: harmonic analysis is carried out to simulate the periodic component of daily rainfall at the Bafing catchment; an ARIMA (4,1,4) process has been identified to model the stochastic component of associated data. Errors from the stochastic modeling are sorted to obtain error pattern reflecting the cyclical behavior of rainfall in the study area. Thus, at each calendar date, error is constituted of ensemble members designed upon one year. Then, a multivariate normal distribution is used to enhance error members after filtering the raw error pattern through the Box-Cox the transformation (Bickel and Doksum 1981; Sakia 1992; Ndione et al. 2018). Statistical errors pattern with enhanced member to 61 is afterward passed on reverse Box-Cox transformation in order to restore initial features of the raw error scheme. Rainfall ensemble forecast is produced using statistical errors to perturb a deterministic forecast from ARIMA model. Further calibrated HBV-light hydrological model is forced with the rainfall ensemble forecast leading to hydrological ensemble forecast referred in this manuscript to as the raw ensemble (RAWEns). In addition, affine kernel dressing (AKD) method is applied to the RAWEns in the purpose of improving quality of RAWEns (Jha et al. 2015; Lucatero et al. 2017; Silverman 1998; Li et al. 2019). Application of the AKD method leads to an additional ensemble referred to as the affine kernel dressing ensemble (D-Ens). Rainfall ensemble is verified by exploratory analysis of time series of the ensemble mean and associated coefficient of determination. Concerning hydrological ensembles (RAWEns and D-Ens) verification is made at deterministic scale using criteria such as the correlation coefficient (Corr), the mean error (ME), the mean absolute error (MAE) and the root-mean-squared error (RMSE) (Quilty et al. 2019). At probabilistic scale, scores (Brier score, rank probability score, continuous rank probability score) and diagrams (attribute and ROC) are used. Both ensembles (RAWEns and D-Ens) present good performances. Nevertheless, results show that the dressing process globally improves the forecast quality, particularly in terms of the resolution and the skill. Improvement has also been highlighted by verifications at deterministic scale.

Materiel and methods

Study area

The Bafing shown in Fig. 1 is the main tributary of the upper catchment of Senegal River which is the second longest river of West Africa. Its area is about 343,000 km2 (Michel. 1973). The Bafing spreads over 38,000 km2, shared between Mali and Guinea countries (Sane et al. 2017; Ndione et al. 2018). It provides about 60% of the Senegal inflow gauged at Bakel station. Its slope and length are about 5 m/km and 670 km, respectively (Maïga et al. 1995). The main source of the Bafing catchment is mountains of Fouta Djallon in Guinea. The climate is of sub-Guinean type in Southern of the Bafing and Sudanese in Northern part (Sane et al. 2017). A multipurpose dam, namely the Manantali one, has been built on the Bafing River for hydropower, low flow support, irrigation, navigability support and flow lamination function (Bader et al. 2015). However, the Manantali dam provides about 12% of electric power consumption in Senegal. The data used in this study are composed of rainfall from the database of the National Civil Aviation and Meteorological Agency of Senegal (ANACIM) and daily flow from the Organization for the Development of the Senegal River (OMVS) database. Daily flow is recorded at the Bafing Makana stream gauge located upstream the Manantali dam. Time series are ranged from 1963 to 1976.

Fig. 1
figure 1

The study area

Full size image

Harmonic analysis of a time series

Time series can be separated into deterministic and stochastic components. The deterministic component is composed of trend and periodic components. The stochastic component characterizes rdom oscillatory behaviors in time series (Kottegoda 1980; Zakaria 2011; Bhakar et al. 2006; Jhajharia et al. 2014). Let us set \(X_{t}\) the studied time series. An additive decomposition of the original time series, namely \(X_{t}\), is formulated as follows (Dabral et al. 2016):

$$X_{t} = {\mathcal{T}}_{t} + {\mathcal{P}}_{t} + \xi_{t} \quad \left( {t = 1,2, \ldots \ldots ,N} \right)$$
(1)

where \({\mathcal{T}}_{t}\) represents the trend component, \({\mathcal{P}}_{t}\) the periodic cone and \(\xi_{t}\) the stochastic component. N characterizes number of observations. In this study, the trend component of the daily rainfall time series has been neglected because of its non-significance according to the Mann–Kendall (M–K). The M–K test (Ndione et al. 2017) has been applied to the daily rainfall series. Result reveals that this time series is trend free: the M–K p value is 0.065. Thus, in the modeling scheme only periodic and stochastic components are analyzed to forecast daily rainfall at the Bafing Makana catchment. It should be kept in mind that for modeling purpose, the different components of the time series are treated separately. Periodic signals such as seasonality in a time series are deterministic in nature. In this paper, the periodic signal is the seasonal behavior in daily rainfall time series. Seasonality in hydrological time series is mainly induced by the rotation and revolution of the earth (Kottegoda 1980) and is modeled in this case of study using harmonic analysis. Considering a time series recorded at regular time step \(\Delta t\), autocorrelogram analysis is further carried out to highlight the periodic behavior within the time series data before performing harmonic analysis for modeling the periodic component. The periodic component referred to as \(P_{t}\) is given by the following equation:

$$P_{t} = \mu + \sum\nolimits_{i = 1}^{p/2} {a_{i} \sin \left[ {\frac{2\pi \tau }{p}i} \right]} + \sum\nolimits_{i = 1}^{p/2} {b_{i} \cos \left[ {\frac{2\pi \tau }{p}i} \right]}$$
(2)

where \(\mu\) defines the average of the daily rainfall; L determines the possible harmonics in the year (fundamental period) which value is obtained by: \(L = n/2\) if n is even and L = \(\left( {n - 1} \right)/2\) if n is odd number. Characteristic coefficients of the basic periodic component are estimates of \(a_{i}\) and \(b_{i}\) of the ith harmonic. The parameter p represents the fundamental period and \(p/i = \lambda_{i}\), the wavelength of associated harmonic with \(i/p\) corresponding to its frequency (Kottegoda 1980). It is important to mention that harmonic analysis at daily scale has more outstanding non-steady frequency shortness than monthly consideration and is strengthened by an ARIMA process. The fundamental period of the daily rainfall time series is p = 365 days. Then, the mean rainfall of the \(\tau\) calendar date is calculated by Eq. (3):

$$m_{\tau } = \frac{n}{p}\sum\nolimits_{i = 1}^{n/p} {x_{{\tau + p\left( {i - 1} \right)}} }$$
(3)

\(n/p\) is the number of years in the whole time series.

Estimated parameters \(\hat{\mu }\), \(\hat{a}_{i}\) and \(\hat{b}_{i}\) are obtained using the least square method and by setting to zero the derivatives of the associated objective function versus fixed parameter \(a_{k}\) or \(b_{k}\). The estimate noticed by \(\hat{\mu }\) represents the average of the daily rainfall. Estimates are calculated with Eqs. 4, 5 and 6 (Kottegoda 1980)

$$\hat{\mu } = \frac{1}{p}\sum\nolimits_{\tau = 1}^{p} {m_{\tau } }$$
(4)
$$\hat{a}_{k} = \frac{2}{p}\sum\nolimits_{\tau = 1}^{p} {m_{\tau } \sin \left( {\frac{2\pi k\tau }{p}} \right)} \quad k = 1,2, \ldots ,\frac{p}{2}$$
(5)
$$\hat{b}_{k} = \frac{2}{p}\sum\nolimits_{\tau = 1}^{p} {m_{\tau } \cos \left( {\frac{2\pi k\tau }{p}} \right)} \quad k = 1,2, \ldots ,\frac{p}{2}$$
(6)

These estimates constitute the basis of the periodic component of the time series which harmonic constitutive variance is given by Eq. (7):

$${\text{var}} \left( {h_{k} } \right) = \frac{{\hat{a}_{k}^{2} + \hat{b}_{k}^{2} }}{2}$$
(7)

Exploratory analysis of the periodogram drawn from variances is done to detect significant harmonics. The periodogram of oscillations is obtained by plotting cumulative variance against rank of associated harmonic. Harmonic significance is weighed by its contribution to the total variance. The number of significant harmonics is obtained considering consecutives ones contributing considerably to the overall variance (Bhakar et al. 2006; Fontin 1987; Kottegoda 1980; Jhajharia et al. 2014).

Modeling of the stochastic component through an ARIMA process

Stochastic component in time series is characterized by random and irregular fluctuations of the series. This component may include deterministic features that are not completely random (Bhakar et al. 2006). The random component in time series cannot be completely determined by physical and deterministic approach. Then, mathematical schemes are performed to model such component (Kottegoda 1980; Fontin 1987, Jhajharia 2014; Quilty et al. 2019). In this paper, the stochastic component of the daily rainfall series is referred to as \(\xi_{t}\). If \(\xi_{t}\) presents a periodicity of 365.25-day or 12-month correlations between data can be taken into account by an autoregressive integrated moving average process with parameters p, d and q \({\text{ARIMA}}\left( {{\text{p}},{\text{d}},{\text{q}}} \right)\) (Eq. 8) with a strictly random residual \(\eta_{t}\). A backshift operator noticed by \({\mathcal{B}}^{{\text{s}}}\) with \({\mathcal{B}}^{s} \xi_{t} = \xi_{t - s}\) introduced to consider existing periodic correlations. ARIMA (p, d, q) process of the stochastic component is defined such that:

$$\phi_{{\text{p}}} \left( {{\mathcal{B}}^{s} } \right)\nabla_{{\text{s}}}^{{\text{d}}} \xi_{t} = \Theta_{q} \left( {{\mathcal{B}}^{{\text{s}}} } \right)\eta_{t} \quad {\text{with}}\quad \nabla_{{\text{s}}}^{{\text{d}}} \xi_{t} = \left( {1 - {\mathcal{B}}^{{\text{s}}} } \right)^{{\text{d}}}$$
(8)

\(\phi_{{\text{p}}}\) and \(\Theta_{{\text{q}}}\) are the autoregressive and moving average parameters, respectively, and p, d and q are orders of the stochastic process.

Ensemble dressing process

In dressing methods, an independent and larger ensemble is drawn from a raw one (Brocker et al. 2008). It is done using an adequate kernel dressing (Gogonel 2013). In the dressing process, ensemble members for given data simulation are dressed by an adequate statistic kernel which mean and variance are either or not fitted (Silverman 1998; Broecker and Smith 2008; Rajagopalan et al. 1997; Li et al. 2019). In addition, dressing methods are used transforming ensemble issues into a continuous distribution function. In this presentation, a dressing method that may overcome shortcomings of the Gaussian density function (Broecker et al. 2008) is used. It is referred to as affine kernel dressing (AKD). The method involves five parameters (\(r_{1}\), \(r_{2}\),\(s_{1}\), \(s_{2}\), a) to dress a new statistical ensemble using estimate mean and variance of the Gaussian kernel (Broecker et al. 2008). Parameters are fitted by minimizing the continuous rank probability score (CRPS) in which process, a logarithm barrier is interposed to overcome problems that are non-negativity of the variance requirement related. The basis of the AKD dressing is to smooth a raw ensemble from an ensemble modeling system. Mean and variance of the kernel dressing are fitted using the five free parameters in addition to the Silverman factor \(\left( {4/3{\text{K}}} \right)^{0.4}\) (Silverman 1998; Ndione et al. 2018):

$${\overline{\text{X}}}_{{\text{d}}} = {\text{ r}}_{1} + {\text{r}}_{2} \left[ {{\overline{\text{X}}}} \right] + {\text{ a}}\left[ {\text{X}} \right]$$
(9)
$$\sum_{\delta \prime } = \left( {4/3K} \right)^{0.4} \left( {s_{1} + s_{2} \times a^{2} \times {\text{var}} \left[ X \right]} \right)$$
(10)

The AKD allows drawing a new continuous distribution function from the K members of the raw ensemble (Eq. 11). The new distribution function of the dressed ensemble is obtained through the following equation expressed as a conditional probability density function such as:

$$p(y/\left[ X \right] ) = \left[ {K\det \left( {\sum_{\delta \prime }^{ - 1} } \right)} \right]^{ - 1} \left( {\sum\nolimits_{i = 1}^{K} {K_{{\text{d}}} \left( {X_{{\text{d}}} } \right)} } \right)$$
(11)

where Kd denotes the Gaussian kernel density.

Ensemble from the AKD process which parameters are fitted minimizing the continuous rank probability score (CRPS) is referred to as D-Ens. Logarithmic barrier that has been introduced to overcome case of negative variance of the Gaussian kernel in the process (Ndione et al. 2018) is given by:

$$\overline{{{\text{CRPS}}}}_{{\text{d}}} = \overline{{{\text{CRPS}}}} \left( {\left[ X \right],{\text{Obs}}} \right) \times \left[ {1 + 0.01 \times \max (0 - \log \left( {\min {\text{Var}} \left( X \right)} \right)} \right]$$
(12)

The HBV-light hydrological model

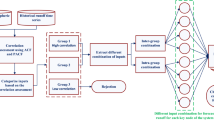
The HBV-light was set up in 1995 and bettered by Jan (Seibert at Uppsala University, Oregon State University, the Swedish University of Agricultural Sciences, Stockholm University and the University of Zurich). It is a semidistributed model in which the studied catchment is divided into subcatchment relatively to different elevations and vegetations. The HBV-light is run using different routines such as the snow routine including snow melt and rainfall, the soil routine based upon the groundwater recharge, the soil storage and the evapotranspiration. A response routine is computed as a function of the water storage (Seiber et al. 2012) to give the runoff of the catchment. Further, another routine–routine one computing the runoff at the catchment outlet is involved in the modeling process. The main inputs are constituted of daily scale data file such as the PTQ file containing precipitation ([mm/Δt]), temperature ([ºC]) and flow discharges ([mm/Δt]). Monthly estimates of long-term variables such the evapotranspiration and the temperature are also involved. These monthly data are linearly interpolated during the simulation process. Explicit description of the model can be found in Bergström (1995), Lindström et al. (1997) and Seibert (1999). The HBV scheme is summarized in Fig. 2.

Fig. 2
figure 2

Structure of the HBV model

Full size image

The model process is briefly described below. Precipitation to be considered depends upon a threshold temperature noticed by TT (ºC). If the temperature is above the TT as noticed in West Africa countries, rainfall is obviously considered. The flux to the ground water box noticed by \(F\left( t \right)\) (mm d−1) is partitioned according to the input to the soil \(I\left( t \right)\) (mm d−1) at a given time step. Each partition is defined as a function characterized by the ratio between the current amount of water in the soil box \(S_{{{\text{SOIL}}}} \left( t \right)\) and its maximum \(P_{{{\text{FC}}}}\) (Eq. 13):

$$\frac{F\left( t \right)}{{I\left( t \right)}} = \left( {\frac{{S_{{{\text{SOIL}}}} \left( t \right)}}{{P_{{{\text{FC}}}} }}} \right)^{\beta }$$
(13)

Estimate of actual evapotranspiration from the soil box is simply equal to the potential evapotranspiration if the ratio of \(S_{{{\text{SOIL}}}} /P_{{{\text{FC}}}}\) is above a value from multiplying maximum water in the soil box and the reduction factor of the evapotranspiration noticed by \(P_{{{\text{LP}}}}\). When above ratio is below \(P_{{{\text{FC}}}} \cdot P_{{{\text{LP}}}}\), estimated actual evapotranspiration (\(E_{{{\text{act}}}}\)) is defined by the following linear reduction:

$$E_{{{\text{act}}}} = E_{{{\text{pot}}}} \cdot \min \left( {\frac{{S_{{{\text{SOIL}}}} \left( t \right)}}{{P_{{{\text{FC}}}} \cdot P_{{{\text{LP}}}} }}, \;1} \right)$$
(14)

Runoff from the groundwater boxes is computed as the sum of linear daily outflows characterized by three parameters noticed by \(P_{{{\text{k}}0}} { },P_{{{\text{k}}1}}\) and \(P_{{{\text{k}}2}}\) that depends on the upper groundwater box \(S_{{{\text{UZ}}}}\) (mm) being above or below a threshold value referred to as \(P_{{{\text{UZL}}}}\) (mm). Runoff of the groundwater box (\(Q_{{{\text{GW}}}} \left( t \right)\)) is given by Eq. (15). Global runoff is transformed into weighted triangular hydrograph function noticed by \(C\left( i \right)\) (Eq. 16). Finally, the simulated daily runoff is obtained by summing the triangular hydrograph scaled by runoff of the groundwater (Eq. 17).

$$Q_{{{\text{GW}}}} \left( t \right) = P_{{{\text{k2}}}} \cdot S_{{{\text{LZ}}}} + P_{{{\text{K1}}}} \cdot S_{{{\text{UZ}}}} + P_{{{\text{K0}}}} \cdot \max \left( {S_{{{\text{UZ}}}} - P_{{{\text{UZL}}}} , 0} \right)$$
(15)
$$C\left( i \right) = \int_{i - 1}^{i} {\frac{2}{{P_{{{\text{MAXBAS}}}} }} - \left| { u - \frac{2}{{P_{{{\text{MAXBAS}}}} }} } \right| \cdot \frac{2}{{P_{{{\text{MAXBAS}}}}^{2} }} du}$$
(16)
$$Q_{{{\text{Sim}}}} \left( t \right) = \sum\nolimits_{i = 1}^{{P_{{{\text{MAXBAS}}}} }} {C\left( i \right) \cdot Q_{{{\text{GW}}}} \left( {t - i + 1} \right)}$$
(17)

The long-term potential evapotranspiration is corrected in the running process, using a weighting coefficient noticed by PCET and the deviation between daily temperature T(t) and associated mean temperature (TM).

$$ \begin{aligned}E_{{{\text{POT}}}} \left( t \right) &= \left( {1 + P_{{{\text{CET}}}} \cdot T\left( {t - T_{{\text{M}}} } \right)} \right) \cdot E_{{{\text{POT}}}} , M \\ &\quad {\text{with }}0 \le E_{{{\text{POT}}}} \left( t \right) \le E_{{{\text{POT}}}} , M\end{aligned} $$
(18)

The performance of the model is evaluated by calculating objective functions such as the model efficiency, the intrinsic flow weighted efficiency and the coefficient of variation given by Eqs. 19, 20 and 21, respectively.

$$R_{{{\text{eff}}}} = 1 - \frac{{\sum \left( {Q_{{{\text{Obs}}}} - Q_{{{\text{Sim}}}} } \right)^{2} }}{{\sum \left( {Q_{{{\text{Obs}}}} - \overline{{Q_{{{\text{Sim}}}} }} } \right)^{2} }}$$
(19)
$$R_{{\text{eff weighted}}} = 1 - \frac{{\sum w\left( {Q_{{{\text{Obs}}}} } \right)\left( {Q_{{{\text{Obs}}}} - Q_{{{\text{Sim}}}} } \right)^{2} }}{{\sum w\left( {Q_{{{\text{Obs}}}} } \right)\left( {Q_{{{\text{Obs}}}} - \overline{{Q_{{{\text{Sim}}}} }} } \right)^{2} }}$$
(20)
$$R^{2} = 1 - \frac{{\sum \left( {\left( {Q_{{{\text{Obs}}}} - \overline{{Q_{{{\text{Obs}}}} }} } \right)\left( {Q_{{{\text{Sim}}}} - \overline{{Q_{{{\text{Sim}}}} }} } \right)} \right)^{2} }}{{\sum \left( {Q_{{{\text{Obs}}}} - \overline{{Q_{{{\text{Obs}}}} }} } \right)^{2} \sum \left( {Q_{{{\text{Sim}}}} - \overline{{Q_{{{\text{Sim}}}} }} } \right)^{2} }}$$
(21)

Verification scores (Brier score, rank probability score and continuous rank probability score)

Brier score

For binary events, the Brier score is used to assess reliability and resolution of predicted probability. The Brier determines the mean squared errors between predictive probabilities \(p_{i}\) at time period \(i \left( {i = 1, \ldots ,N} \right)\) and the binary observations \(o_{i}\) which value is 1 when observation is below the threshold value \(x_{t}\) and 0 otherwise at time period (Addor et al. 2011; Randrianasolo et al. 2011; Ndione et al. 2018; Sharma et al. 2018). The Brier score that corresponds to the mean squared error in deterministic forecasts is given by the following formula:

$${\text{BS}} = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\left( {p_{i} - o_{i} } \right)^{2} }$$
(22)

Mathematically, the lower the Brier score value, the best is the ensemble forecasting system. Thus, optimum Brier score corresponds to zero for perfect forecasting that means all expected scenarios are observed. The BS can be decomposed into three components: reliability, resolution and uncertainty (Murphy 1973; Candille 2005; Ndione et al. 2018). The decomposition consists of considering \({\text{N}}_{{\text{K}}}\) clusters among the \({\text{K}}\) ensemble members which is probability \(p_{{\text{s}}}\). It is done to show characteristics of model quality. The decomposition is such that: BS = reliability − resolution + uncertainty. Reliability assesses the distance between forecast ensemble and mean of observations. The resolution measures how different predicted distribution categorized the observations. Thus, wide resolution means possibly clustering observations to categories with considerable difference. Uncertainty in the BS decomposition highlights the variability of forecast data and does not impact the model reliability. The BS has been generalized to multiple categories (discrete rank probability score) and continuous scalar variables (continuous rank probability score). The RPS is based on comparison between cumulative distribution functions of the forecasts and one of observations in subsequent percentiles. The cumulative distribution function of the observations is represented by a cumulative function which is probability density taken the value of 1 when the probability threshold is exceeded and 0 otherwise (Epstein 1969; Murphy 1973; Vincendon 2011; Ndione et al. 2018). The RPS is obtained by summing the Brier score at different percentiles (10%,…, 30%,…, 90%). This approach is useful for categorizing the river discharges. For example, in flow classification, the following decomposition can be retained: low flows (< 10%), medium flows (10% < Q < 90%) and high flows (> 90%) (Zalachori 2013). Thus, different probabilities can be obtained for an ensemble according to chosen percentiles. Let N be the spread of the ensemble forecast which Brier score is calculated for M categories of the ensemble determined containing m members. The rank probability score at lead time \(\mathrm{i}\) is given by:

$${\text{RPS}}_{i} = \sum\nolimits_{m = 1}^{M} {\left( {\sum\nolimits_{j = 1}^{m} {\left( {p_{i,j} - o_{i,j} } \right)}^{2} } \right)}$$
(23)

Pi,j denotes the forecast probability of category m at time i, oi,j represents binary variable which value 1 when the category \(m\) is observed and 0 if associated category is not observed at time \(i\). Thus, the RPS over the forecasting period is obtained through the following formula (Ndione et al. 2018; Shin et al. 2019):

$${\text{RPS}} = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {{\text{RPS}}_{i} }$$
(24)

For continuous variables, the continuous rank probability score that is an extension to infinity of the discrete rank probability score is often used. The CRPS computes the global quality of issued ensemble forecast. It measures the distance between the ensemble forecast and the observed events. In the CRPS computing, the \(\mathrm{M}\) categories of the \({\text{RPS}}_{i}\) (Eq. 2) are stretched to infinity (Matheson and Winkler 1976; Hersbach 2000; Zalachori 2013). Variables involved in the estimating of the CRPS are: the cumulative distribution function of the forecasted values noticed by \(F_{i}^{f}\) and other one cumulative distribution function, noticed by \(F_{i}^{0}\), which value is 0 when the forecast is lower than the observation and 1 otherwise (Heaviside function). The equation of the continuous rank probability score (CRPS) is formulated as follows (Marty 2013; Casati et al. 2008; Bellier and Win 2017; Ndione et al. 2018; Awol et al. 2019):

$${\text{CRPS }}\left( x \right) = \frac{1}{N}\sum\nolimits_{i = 1}^{N} {\int_{x = + \infty }^{x = - \infty } {\left( {F_{i}^{f} \left( x \right) - F_{i}^{0} \left( x \right)} \right)^{2} dx} }$$
(25)

\(F_{i}^{f} \left( x \right)\) is the cumulative distribution function of the forecasts, \(F_{i}^{0} \left( x \right)\) is the Heaviside function, N is the number of the time step.

Verification diagrams (attribute diagram and ROC curve)

Reliability, resolution and skill of an ensemble forecasting system can be visualized through the attribute diagram. The diagram shows the position of a curve representing the predictive probabilities against the relative frequency of the occurrences relatively to the no-resolution line, perfect forecast (line 1:1) and no skill ones. Attribute of ensemble forecasting shows the reliability of implemented system, its resolution (skill of the system in considering higher and lower probability of events) and the uncertainty of issued ensemble with reference to observations. Attribute diagram is obtained by plotting the relative frequency of the observations against the forecast probabilities (Wilks 2006; Ndione et al. 2018; Shin et al. 2019). Relatively to attribute diagram, a perfect forecast exactly fits the first bisector (line 1:1). Uncertainties are defined for a given threshold, by the distance between categories and the first bisector characterizing perfect model. The resolution estimates how forecasts differ to the climatological mean probabilities of the events (sample climatology), and how the systems get it right. More, it defines the ability of the model to issue reliable probabilistic forecast close to 0 and to 1.

The ROC (relative operating characteristic curve) curve allows evaluating separation of means of conditional distribution of some simulated data and is a very popular tool in decision-making approaches. The ROC is positive when the curve is beyond the first bisector which area under the ROC (AUC) is of 0.5. Perfect modeling corresponds to AUC of 1. The AUC defines the probability of successfully discriminating an event from a non-event (Mason 1982; Atger 2006; Awol et al. 2019). Given a threshold probability, forecasts are sorted into hits, misses, false alarm and correct rejections classes. Then, the ROC curve is obtained by plotting the false alarm rate against hit rate. This is a popular tool in decision-making supports. Thus, false alarm and hit rates are given as follows:

$${\mathbf{F}}_{{{\mathbf{ar}}}} = \frac{{\text{False alarm}}}{{{\text{False alarm}} + {\text{correct rejection}}}}$$
(26)
$${\mathbf{H}}_{{\mathbf{r}}} = \frac{{{\text{Hit}}}}{{{\text{Hit}} + {\text{miss }}}}$$
(27)

Results and discussion

Assessment of deterministic and ensemble forecast

The coefficient of determination between the mean forecast rainfall series to be used as HBV input and observations is of about 0.92 (Fig. 3). Further, correlation between them is also shown in Fig. 3. Analysis of these results shows that the ARIMA (4,1,4) is capable of providing likely daily rainfall of the Bafing catchment. The coefficient of determination exhibits adequacy in time between simulations and observations. Deterministic forecasts for daily rainfall of year 1976 and simulations in the calibrating period are summarized in Fig. 4. Analysis of the figure confirms good representation of daily rainfall by the retained stochastic model. Stochastic model of the daily rainfall is perturbed to obtain rainfall ensemble forecast represented in Fig. 5. It globally fits rainfall behavior at the Bafing catchment.

Fig. 3
figure 3

Linear evolution of the deterministic forecast and verifications

Full size image
Fig. 4
figure 4

Evolution of deterministic simulations and forecasts against observations

Full size image
Fig. 5
figure 5

Evolution of rainfall ensemble forecast against observations

Full size image

Assessment of the hydrological ensemble forecast

The HBV model has been calibrated in advance to fix optimum parameters before ensemble forcing procedure. Evolution of simulated deterministic flow discharges and forecasts (Qsim) against observations (Qobs) is shown in Fig. 6 with a model efficiency of about 0.74, coefficient of determination of about 0.77 and flow weighted efficiency of about 0.8. According to evaluating parameters, the HBV model is well calibrated in comparison with results from Ali et al. (2018), where \(R^{2}\) and \(R_{{{\text{eff}}}}\) are about 0.92 and 0.85, respectively. Further, calibrating HBV in this study is more representative than ones given in Mendez et al. (2016) concerning three catchments: Reventado (R2 = 0.547), Purires (R2 = 0.716) and Toyogres (R2 = 0.638). In fact, the HBV model has been performed in this study to issue hydrological ensemble forecast. It is important to highlight that the same parameters have been retained throughout the process of the ensemble issuing. Variation of the ensemble forecast and observations is shown in Fig. 7.

Fig. 6
figure 6

Evolution of simulated and observed discharge

Full size image
Fig. 7
figure 7

Variation of the model performances with different members of forecasted rainfall series

Full size image

During the ensemble discharges forecasting, deterministic performance characteristics such as the coefficient of variation, the model efficiency and the flow weighted efficiency are used to evaluate the HBV runs. Evolutions of above characteristics in the process are presented in Fig. 7. Indeed, through the ensemble forecasting system performing, efficiency of the HBV varied from 0.53 to 0.83, the coefficient of determination from 0.73 to 0.80 and the flow weighted efficiency from 0.65 to 0.81 (Table 1). During the procedure, the model efficiency is more subject to variations than both other coefficients (determination and flow weighted efficiency). Averages of the above HBV evaluating criteria are 0.74, 0.8 and 0.77, respectively. Faire variation of the coefficients of determination and the flow weighted efficiency has been noticed in spite of a significant variation of the model efficiency relatively to the input variations.

Table 1 Coefficient of variation, the model efficiency and the flow weighted efficiency during the process
Full size table

In this paper representation of the hydrological ensemble forecast is made to give an overview upon the ensemble behavior in time. Evolution of the ensemble is presented in Fig. 8. Exploratory analysis of this figure gives an overview on the representativeness of the daily ensemble flow discharges forecasts upper the Manantali dam. The ensemble is assumed to be of good representativeness with reference to ensemble evolution in Bartholmes et al. (2005) and also in Quilty et al. 2019. This analysis allows assuming without assessment of the statistic verifications the skillfulness of the hydrological ensemble forecasting system.

Fig. 8
figure 8

Evolution of the hydrological ensemble forecasting from the HBV-light model

Full size image

Ensemble characteristics and scores

Globally, analysis of the statistical performances shows that the postprocessing method has enhanced the performance of the model as at deterministic scale (ME, MAE, RMSE) than at probabilistic scale (Brier score, rank probability score and continuous rank probability score). Correlation (EnsCorr) between time series of the ensemble mean and one of observations is the same. Deterministic criteria are acceptable when compared with others in the literature such as the correlation between forecasts and observations of 0.8, ME of 1.04 and RMSE of 5.33 for a long-term forecast study in Gelfan et al. (2017). Otherwhere, a ME of about 0.06 has been obtained in Davison et al. (2017). Further, in Jeong et al. (2005), RMSE of 0.346 has been retained for a single neural network (SNN) forecast and of 0.319 for an ensemble forecast produced by an ensemble neural network (ENN) system. For both systems in this study, the Brier scores are approximately the same: 0.094 for the RAWEns and 0.090 for the D-Ens. From performed ensembles, probabilistic issues have been produced applying tertile clustering to the ensemble members and binarizing associated observations. Thus, three categories of the simulations are drawn for each calendar date and the first category is retained with its associated probability. Probabilistic forecast leads to acceptable scores for two ensembles (RAWEns and D-Ens). The best continuous rank probability score (CRPS) is of 0.149 (D-Ens). The RPS of the two ensembles is of 0.133 for the D-Ens and of 0.282 for the RAWEns. Detailed results concerning probability scores of ensembles including resolution and reliability of ensembles schemes are shown in Table 2 and Table 3. In the literature, scores of 0.13 for the BS, of 0.28 for the BSS and of 0.054 for the RPS have been obtained for a long-term ensemble forecast of snowmelt inflow into the Cheboksary reservoir under the differently constructed weather scenarios (Gelfan et al. 2017). CRPS of 0.10 and 1.8 have been obtained for a short-term hydrological prediction in Davison et al. 2017. Thus, in terms of accuracy, the forecasting systems in this study can be considered as very good. Resolution, reliability according to the Brier score (BSReli) and the rank probability score (CRPSReli), uncertainty and area under the ROC curves (AUC) are given in Table 3. Scores are very satisfactory in comparison with ones in Hersbach 2000 where the CRPSReli is ranging from 0.015 to 0.068 and resolution from 0.073 to 0.322 within ten days. Evaluating probability scores reveals that the systems issuing the raw ensemble in this study and the one producing D-Ens provide very good performances in terms of reliability, resolution and skill and then can be used in planning the flow discharges releases or lamination at the Manantali dam. In other words, both ensembles can be used in decision making by the dam administrators. Nevertheless, in this case of study, the postprocessing (affine kernel dressing) method involving enhances model performances.

Table 2 Deterministic verifications and probability scores
Full size table
Table 3 Attributes of the forecasting systems
Full size table

Attribute and reliability diagrams and ROC plots

The attribute diagram is obtained by plotting the forecast probability against relative frequency of the observation. Attribute diagram shows simultaneously in a visible manner reliability, resolution and uncertainty of an ensemble forecasting system. For perfect forecasting, the plot fits the first bisector (line 1:1). Reliability diagrams of the two models are presented in Fig. 8a and c. The ROC curve is used to assess the rate of successes (Hits) of the model, and the one of its failure cases has been plotted for two ensemble forecasting schemes. For both systems (RAWEns and D-Ens), hits prevail on false alarm rates. Area under the ROC (AUC) is of 0.962 for the system giving the RAWEns and of 0.963 for the ensemble from the affine kernel dressing method. AUCs values confirm reliability of schemes with reference to AUC of about 0.94 in Gelfan et al. 2017. Results (AUCs) are in spite of scale and context differences, comparable to better ones in Roux et al. 2020, where two hydrometeorological ensemble strategies for flash-flood forecasting are evaluated. Nevertheless, two systems are skillful in forecasting flow discharges upper the Manantali dam. Indeed, system skillful is based on the prevalence of hits rates on false alarm ones for most of the probability thresholds (Fig. 9b and d). Attribute diagrams show good performance for the two ensemble systems performed with the same baseline equal to 0.333: the raw ensemble (RAWEns) and the D-Ens providers. So, dressed ensemble scheme providing the D-Ens (Fig. 9c) is better. Both ensemble systems (RAWEns and D-Ens) give more success than failures for the probabilistic forecast of the flow discharges and can be used to enhance flow monitoring at the Manantali dam. Elsewhere, through ROC curves decision making can be improved particularly when facing to extreme events (drought or flood). Using the probabilistic interpretation of the results decision makers of the Manantali dam may have argument on the opportuneness of engaging flow support or flow lamination.

Fig. 9
figure 9

Attribute diagram and ROC curve for both RAWEns and D-Ens

Full size image

Conclusion

Hydrological ensemble forecasting system is an ingenious way to quantify uncertainties in hydrological forecasting. Uncertainties are considered through probabilistic forecasts. This is achieved by issuing an ensemble of possible values of the forecast variables by propagating an ensemble of input through a hydrologic model to provide an ensemble of output. In this study a hydrological ensemble forecasting system is set up to predict flow discharge of the Bafing Makana River (Senegal) upper the Manantali dam for the year 1976 using rainfall forecast from stochastic perturbation and HBV-light model. The affine kernel dressing method is applied to the raw ensemble in order to improve the quality of the forecasts. The HBV model was calibrated in the period ranging from 1963 to 1975. Cyclical errors from the ARIMA process in forecasting rainfall are used to construct error pattern. Error pattern is then used to perturb rainfall forecast from ARIMA modeling that leads to a rainfall ensemble forecast. Indeed, the error pattern is designed on the basis of the periodic behavior of rainfall at the Bafing over 365 days. Box-Cox transformation is used to normalize the raw error pattern in order to generate wide members through a multivariate Gaussian kernel. Reverse Box-Cox transformation is afterward applied to restore initial features of the errors pattern. Drawn rainfall ensemble is used to force already calibrated HBV-light model to produce hydrological ensemble forecast. From the above procedure, ensemble streamflow which members are of 61 including the ensemble mean is performed. From the postprocessing tools, another ensemble (D-Ens) is drawn in addition to the raw ensemble (RAWEns) from forcing of the HBV. According to different scenarios and both coefficients of determination and flow weighted, efficiency varies from 0.73 to 0.80 and from 0.65 to 0.81, respectively; the model efficiency is ranging from 0.53 to 0.83. Ensemble forecast verification tools are used to evaluate the reliability, the resolution and the skill of implemented ensemble forecasting systems. Results are well convincing in terms of reliability and skill. Correlation between forecasted ensemble and observation is of about 0.87 for both processed (D-Ens) and not processed ensemble (RAWEns). For both ensembles, correlation between the ensemble mean and the observations is of 0.871. Brier scores, continuous rank probability scores and area under ROC curves are, respectively, 0.094, 0.282 and 0.962 for the RAWEns model and 0.090, 0.149 and 0.963 or the D-Ens model. Verification values of both ensembles in this study have indeed been compared with others in the literature (Ali et al. 2018; Mensez et al. 2016; Bartholmes et al. 2005; Gelfan et al. 2017; Davison et al 2017; Hersbach 2000) for more exhibiting effectiveness the used approaches. Then, considering probabilistic scores ensemble can be used to improve decision making at the Manantali dam.