Introduction

The rainfall–runoff modelling is an important and useful tool for hydrological research, water engineering and environment application. The runoff computation from ungauged or poorly gauged catchments is a serious challenge in developing countries like India where higher operation and maintenance cost differed gauging on small and medium rivers. The knowledge-based or data-driven hydrological models were developed and used by researchers to extend runoff records and address modelling issues (Kar et al. 2015, 2017). The hydrological model can be classified into three broad groups, namely metric, physical and conceptual models (Beck et al. 1990). The rainfall–runoff relationships in metric models are essentially based on observations and without characterizing different processes involved in the hydrologic system (Kokkonen and Jakeman 2001). The linearity assumption-based unit hydrograph theory (Sherman 1932), catchment characteristics-based rational formula for peak runoff given by JM Thomas (1822–1892) and reproduced by Loague (2010), Strange tables, etc., are some of the examples of metric modelling. The metric models are observation-based models developed using observed runoff and catchment characteristics without considering much of hydrological processes. The physical models represent different hydrological processes through mass, momentum and energy conservation equations. The physical models may be capable of considering the spatial variability of land use, slope, soil and climate to deal with the hydrological processes within the watershed semi- or fully distributed in nature.

The conceptual models are hydrological models that use simplified mathematical conceptualization of a system with the help of a number of interconnected storages used to represent different components of the hydrological process through recharge and depletion. The conceptual models are usually lumped in nature and use the same value of parameters for the whole watershed and ignored the spatial variability of watershed characteristics. The conceptual models strongly rely on observed data, and results depend on the quality of input data used in the model. Large numbers of conceptual models have been proposed in the past including Sacramento model (Brazil and Hudlow 1981), Clark model (Clark 1945), Nash model (Nash 1957), HBV model (Bergstrom 1992, 1995), HYMOD (Moore 1985), watershed model (Crawford and Linsley 1966), TANK model (Sugawara et al. 1974, 1983), Boughton (1984) model, MODHYDROLOG (Chiew and McMahon 1994), HEC-1 (Burnash et al. 1973), Xinanjiang model (Zhao and Liu 1995), ARNO model (Todini 1996), etc.

The physical models represent different hydrological processes through mass, momentum and energy conservation equations. The finite difference or finite computation schemes are generally used to solve governing partial difference equations in these models. The physical models may be capable of considering the spatial variability of land use, slope, soil and climate to deal with the hydrological processes within the watershed semi- or fully distributed in nature. As physical models are distributed in nature, they require large amount of topographical, soil, land use and climatic data to provide a framework to explore the changes in hydrological cycle due to human interferences and climate change for water resources management (Leavesley 1994; Jiang et al. 2007; Yang et al. 2008, 2014; Praskievicz and Chang 2009, Wang et al. 2010; Chen et al. 2016). At the same time, these models can depict complex hydrological processes and predict different components of the hydrological cycle with an acceptable limit of efficiency. The TOPMODEL (Beven and Kirkby 1976, 1979; Beven et al. 1995), SHE (Abbott et al. 1986a, b), ISBA (Nolihan and Planton 1989; Nolihan and Mahfouf 1996), SLURP (Kite 1995), MIKE SHE (Refsgaard and Storm 1995); SWAT (Arnold et al. 1998a, b), DPHM-RS (Biftu and Gan 2001, 2004); TOPNET (Bandaragoda et al. 2004), MISBA (Kerkhoven and Gan 2006), HydroGeoSphere (Therrien et al. 2006), PIHM (Qu and Duffy 2007), CATFLOW (Zehe et al. 2005; Klaus and Zehe 2010), CREST (Wang et al. 2011), variable infiltration capacity (VIC) (Wood et al. 1992; Liang et al. 1994; Lohmann et al. 1998) models are some of the most commonly used semi- or fully distributed physical models. The comparison of conceptual and physical models is presented in Table 1.

Table 1 Comparison of conceptual and physical models
Full size table

Vaze et al. (2012) have analysed strength and weakness of different types of models and concluded that metric and conceptual models are suited for daily timescale while physical models can be used on daily as well as the sub-daily timescale. The requirement of high-resolution spatial and other data is low for metric models, moderate for the conceptual model, while high to very high in case of semi-distributed and fully distributed physical models. Similarly, metric models may have 1 to 5 parameters; conceptual models may have 4 to 20 parameters, while fully distributed models can have 10 to 1000 parameters to be adjusted for calibration. Haque et al. (2015) have quantified different uncertainties of rainfall–runoff modelling with AWBM in a gauged catchment and an ungauged catchment. In the study, five rainfall data sets, twenty-three different calibration data length and eight optimization techniques for gauge catchment have been employed and extended to the ungauged catchment using two regional prediction equations. The uncertainties were compared with observed and model runoff by the AWBM and varied from 1.3% to 70% in input rainfall data, 5.7% to 11% in calibration and 6% to 0.2% in optimization technique. Zhang et al. (2016) have applied the Australia water balance model (AWBM) and simple multiple regression to model stream flows in five tributaries of the Poyang Lake basin. The results indicated that multiple regression models were appropriate with precipitation, and potential evapotranspiration of the current month and precipitation of the last month were explanatory variables, but AWBM gave higher Nash–Sutcliffe efficiency.

Kumar et al. (2015) discussed the application of different conceptual and semi-distributed model for application in a basin which used different kinds of model parameter and input data. In order to select the best model, MIKE SHE, SWAT, HEC-HMS, AWBM, SIMHYD, Sacramento, SMAR and TANK models along with linear programming (LP) were used, and it was found that an ensemble exhibited comparative results with the order of SWAT, AWBM, HEC-HMS, SIMHYD and Sacramento for the performance on a selected catchment. Shoaib et al. (2018) discussed that rainfall–runoff modelling through a stochastic process which depends on climatologically variable and catchment characteristic. Onyutha (2016) applied five conceptual hydrological models including AWBM, TANK, SIMHYD, Sacramento and IHACRES in Blue Nile basin for rainfall–runoff simulation. The Nash–Sutcliffe efficiency was used as a goodness-of-fit measure for selecting the best model. They suggested that the choice of model should be made on the basis of the objective of modelling.

The SWAT model has several tools; interfaces and supporting software have been developed in the last 20 years making this software more versatile. The latest developed SWAT-CUP has the capability of sensitivity and several optimization techniques like GLUE, Parasol, SUFI2, MCMC and PSO. The main weakness of the model is the requirement of a wide range of data and non-spatial representation of the HRU inside each sub-catchment. Glavan and Pinter (2012) described strength, weakness, opportunities and threat (SWOT) of SWAT model and described the strength of SWAT model as an easily available online model that can combine water quality, quantity, agriculture land management, and climate change simultaneously. Khoi and Thom (2015) have applied SWAT model and SWAT-CUP application using generalized likelihood uncertainty estimation (GLUE), parameter solution (Parasol), particle swarm optimization (PSO) and sequential uncertainty fitting (SUFI2) techniques for uncertainty analysis in the catchment of river Srepok of Vietnam. The results of the analysis indicated that among all the methods, SUFI2 may be the most suitable method as it required the smallest runs to get appreciable prediction and model performance. Similarly, several other researchers have compared different techniques of optimization and uncertainty for SWAT model and found SUFI2 can predict the runoff reasonably well with the smaller number of simulations (Wu and Chen 2015; Uniyal et al. 2015; Mamo and Jain 2013).

Looking into the strength and weakness of different conceptual and semi-distributed physical models, the present study deals with the comparative evaluation of some conceptual and distribute models for performance in an Indian basin having problems of availability of data.

Material and methodology

Study area

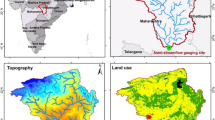
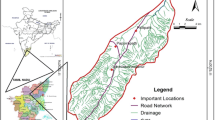
The study area for the present study is Tandula catchment up to Tandula reservoir in the Chhattisgarh state of India. Tandula reservoir is situated on the confluence of river Tandula with Sukha Nala in Balod district having a catchment area of 827.2 km2. The location map of the study area has been presented in Fig. 1. The Tandula dam has been constructed in the year 1921 and presently irrigating 82,095 ha paddy fields along with the supply of industrial water to Bhilai Steel Plant at Durg and other domestic supplies to several tanks in the command. The Tandula catchment is influenced by four rain gauge stations including Balod, Bhanpura, Chamra and Gondli in and around the catchment with the Thiessen weight of 0.18, 0.39, 0.25 and 0.18, respectively.

Fig. 1
figure 1

Location map of Tandula catchment in Chhattisgarh state of India

Full size image

Data used

The daily reservoir level, releases and overflow from weir for the period from 1991 to 2015 have been used in a simple water balance model to compute daily runoff from the catchment. The rainfall data of Balod, Bhanpura, Chamra and Gondli and climatic data of Raipur have been used in the analysis. The land use of the study area has been determined using multiple LISS III data from IRS satellite. The climatic data of Raipur climatic station were used in rainfall–runoff modelling. The soils have been identified from literature review and maps from All India Soil Survey & Land Use Planning (AISSLUP, Nagpur).

Methodology

In the study, two conceptual models (TANK model and AWBM ) available in Rainfall Runoff Library (RRL) and developed by Co-operative Research Centre for Catchment Hydrology (CRCCH), Australia and a semi-distributed model (Soil and Water Analysis Tool) have been evaluated for their performance in Tandula basin of India. The RRL was developed using practical experience of CRCCH research and freely available on http://www.toolkit.net.au/Tools/RRL. The RRL library is capable of modelling hydrological processes in the catchment using models such as AWBM, Sacramento, SIMHYD, SMAR and TANK. The parameters of these models can be optimized using any one of the techniques including uniform random sampling, genetic algorithm (GA), shuffled complex evaluation (SEC-UA), pattern search, multi-start pattern search, Rosenbrock search and Rosenbrock multi-start search. The calibration and validation of these models can be done with any one of ten different objective functions including Nash–Sutcliffe efficiency (Nash and Sutcliffe 1970), sum of square error, root-mean-square error, root-mean-square difference about bias, absolute value of bias, sum of square roots, sum of square of the difference of square root and sum of absolute difference of the log-transformed data. The SWAT is a semi-distributed physical model capable of modelling hydrological processes including quantity, quality and sediment in a basin. The SWAT model is a widely used model for runoff, recharge, sediment and nutrient flow in the basin. The description of TANK, AWBM and SWAT applied in the analysis is presented below.

TANK model

The TANK model in RRL consists of four vertical tanks in series where precipitation and evaporation are used as inputs in the top tank and evaporation is subtracted sequentially from all the tanks. In this model, the top tank has two outlets, while all other tanks have only one outlet with runoff coefficient axy at variable heights Hxy. Here, x is the number of tank and y is the number of outlets (Fig. 2). The total runoff is computed as the sum of runoff from all the tanks using the following equation:

$$q = \mathop \sum \limits_{x = 1}^{4} \mathop \sum \limits_{y = 1}^{nx} \left( {C_{x} - H_{xy} } \right)a_{xy}$$
(1)

where q is the runoff in mm, Cx is the level of water in the xth tank, Hxy is the height of the yth outlet in the xth tank. The actual evapotranspiration (ETA) from each tank is the loss from the system and can be computed based on the depth of water (Cx) in xth tank. The following equation can be used to compute actual evapotranspiration (ETA) for a tank.

Fig. 2
figure 2

(Reproduced from RRL manual)

Structure of TANK Model in RRL.

Full size image
$${\text{ETA}} = {\text{ETP}}\left( {1 - {\text{e}}^{{ - \propto \sum C_{x} }} } \right)$$
(2)

The infiltration (Ix) in these tanks can be computed using tank-wise infiltration coefficient (bx) and water levels in the corresponding tank with the help of the following equation:

$$I_{x} = C_{x} b_{x}$$
(3)

The sum of runoff computed from different tanks can be considered as total runoff from the basin. The first tank gives surface runoff, second tank intermediate runoff, while third and fourth tanks provide sub-base and base flow, respectively. The different parameters, their default value and range of TANK model have been presented in Table 2.

Table 2 Range and default values of parameter in TANK model
Full size table

AWBM model

The AWBM works on the basis of three independent surface storages for computation of partial runoff from a catchment (Fig. 3). The model independently calculates water balance for each surface storage using precipitation and evapotranspiration as inputs. The whole catchment in this model can be divided into three partial areas using three parameters as A1, A2 and A3. The soil moisture for each partial area is computed by adding precipitation and deducting evapotranspiration. At any time, rainfall is added to each of the partial area or storage and after deducting evapotranspiration, the following water balance equation is used to compute storage and if the moisture becomes greater than the capacity of storage, the moisture in excess of capacity becomes runoff.

Fig. 3
figure 3

(Reproduced from RRL manual)

Structure of AWBM in RRL.

Full size image
$$S_{n} = S_{n - 1} + P_{n} - {\text{EVT}}_{n}$$
(4)

where Sn−1 and Sn are the storage on n − 1 and nth days, Pn and EVTn are the precipitation and evapotranspiration on nth day. In this model, friction (BF1) of runoff in any partial storage gave base flow and reminder may provide surface runoff from that store using following equations.

$${\text{BS}}_{t} = {\text{excess}}\,*\,{\text{BF}}_{1}$$
(5)
$${\text{SS}}_{t} = {\text{runoff}}\,*\,\left( {1 - {\text{BF}}_{1} } \right)$$
(6)

Both the surface runoff from three partial storage and base flow are depleted on daily or hourly timescale with the help of surface flow recession coefficient (KS) and baseflow recession coefficient (K) in a linear manner using the following equations:

$${\text{SS}}_{t} = \left( {1 - K_{\text{S}} } \right){\text{SS}}_{t - 1}$$
(7)
$${\text{BS}}_{t} = \left( {1 - K_{\text{B}} } \right){\text{BS}}_{t - 1}$$
(8)

The routed surface and base flow at the outlet of the basin provide total runoff from the basin. The different parameters of AWBM along with the range are given in Table 3.

Table 3 Range and default values of parameters in AWBM
Full size table

SWAT model

The SWAT model (Arnold et al. 1998a, b; Neitsch et al. 2001, 2002) is a physically distributed parameter and continuous time simulation basin scale supported by USDA Agricultural Research Service (USDA-ARS) at the Grassland, Soil and Water Research Laboratory, Texas, developed to predict the response to natural inputs as well as the manmade interventions and management practices such as fertilizer application, livestock grazing and harvesting operation on water, sediment and agriculture chemical yields in gauged as well as ungauged catchments. The model works on daily/sub-daily time step, able to simulate land management and runoff processes using spatial distribution of land use, soil and topography by dividing basin into sub-basins and hydrological response units (HRUs). Each sub-basin in the SWAT model may have an organization of climate, HRUs, ponds/wetlands, groundwater and main channel/reach draining the basin. The land use, soil, digital elevation model, climatic data are the prime input for the model, and it is able to predict sub-basin-wise runoff, groundwater contribution, base flow, crop growth, soil erosion, sediment yield, nutrient status, etc. (Santhi et al. 2006).

The runoff volume in the SWAT model is estimated by Soil Conservation Services (SCS) curve number technique. The runoff yield for individual HRU and then for sub-watersheds are routed through river network using variable storage or Muskingum routing method. The complete detail about the SWAT model and its application are available in Neitsch et al. (2001, 2005). The model have hundreds of parameters for defining the spatial variability of hydrological characteristics of the basin, out of which some of the parameters vary by sub-basin, land use, or soil type, while others can be computed through field measurement, data or literature. The SWAT model works on the principle of water balance, and two major components of the hydrological cycle are computed considering physical process within the basin. The first phase computes the runoff, sediment, nutrients and pesticide loading to the main channel of each basin, while the second phase concentrates on routing for movement of generated runoff, sediment, nutrient and pesticide through a network of the channel to the outlet of the basin. The different components of the hydrological cycle in the SWAT model can be represented by the following water balance equation:

$${\text{SW}}_{i} = {\text{SW}}_{0} + \mathop \sum \limits_{i = 1}^{t} (P_{i} - {\text{SQ}}_{i} - {\text{ET}}_{i} - Wseep_{i} - Qgw_{i} )$$
(9)

where SWo and SWi are the soil water content in mm of H2O at initial and tth day, respectively, Pi, SQi, ETi, Wseepi and Qgwi are the precipitation, surface runoff, evapotranspiration, water enter into the vadose zone and return flow in terms mm of H2O on the ith day, respectively. The runoff computed for each HRU is routed to get total runoff at the outlet of the basin. The SWAT model has options for computation of surface runoff either using modified SCS curve number method or Green and Ampt method. The input precipitation in the model first undergoes interception and is computed by the canopy in the SCS curve number method or user-defined leaf area index in case of Green and Ampt method. The infiltration in the SWAT model can be computed either directly through Green and Ampt method or by the remaining amount of water from precipitation after generation of daily runoff in case of SCS method. The following formulae are used to predict surface runoff using the SCS-CN method.

$$Q = \frac{{\left( {P - I_{\text{a}} } \right)^{2} }}{{\left( {P - I_{\text{a}} + S} \right)}}$$
(10)

where \(I_{\text{a}} = 0.2S\) for antecedent moisture condition II (AMC II), Q is the surface runoff in mm, P is the rainfall in mm, Ia is the initial abstraction, S is the surface retention and can be computed by the following equation.

$$S = \frac{25400}{CN} - 254$$
(11)

where CN is the curve number depends on soil type, land use, management practices and antecedent moisture condition. The CN values as defined in SCS method are used in the model and modified for antecedent moisture condition I (dry condition), II (average condition) or III (wet condition) in the model. For computation of evaporation from soil and water separately, the method suggested by Ritchie (1972) is used, while the options of Hargreaves method (Hargreaves et al. 1985), Priestley–Taylor method (Priestley and Taylor 1972) and Penman–Monteith method (Monteith 1965) are available for computation of potential evapotranspiration. The water percolated to the bottom root zone is partitioned in interflow and baseflow. The lateral subsurface flows or interflow is computed using a kinematic storage model in each soil layer, while baseflow or groundwater is muddled using two aquifer systems in the SWAT model. The topmost aquifer which is considered as unconfined aquifer contributes return flow within the watershed, and underlined deep aquifer contributes outside of the watershed (Arnold et al. 1993). The baseflow is only allowed when the amount of water stored in shallow aquifer reached to a prescribed level defined by the user and then baseflow which is the contribution to the main channel or reach is computed using the study-state response of groundwater flow suggested by Hooghoudt (1940).

Comparative evaluation of performance

The application of models whether simple or complex depends on how well they can reproduce the response of the system. The Nash–Sutcliffe efficiency (NS), the coefficient of correlation (Cc) and root-mean-square error (RMSE) were used as the goodness-of-fit criterions for selecting an appropriate model.

Results and discussion

The RRL library has been used to set up conceptual models like TANK model and AWBM , while the SWAT model in Arc GIS and SWAT-CUP application have been employed as a physical model for Tandula basin. Before carrying out modelling, a daily water balance of Tandula reservoir has been carried out for computation of runoff for the period of 25 years from the year 1991 to 2015 and used as input to these models. The results of the application of AWBM, TANK model and SWAT model are presented below.

Conceptual models

TANK model

The aerial rainfall series based on Thiessen weight of different stations and evapotranspiration computed from climatic data of Raipur station were used as inputs to the TANK model where data from 1991 to 1994 have been used for warming, 1995 to 2004 for calibration and 2005 to 2015 for validation of the model. The auto-calibration has been done for optimization of parameters of the model, and then, genetic algorithm (GA) has been used to get further refined values of parameters. The optimized parameters of TANK model have been presented in Table 4. The graphical representation of observed and computed runoff obtained from TANK models during calibration and validation has been presented in Fig. 4. The Nash–Sutcliffe efficiency of the model during calibration and validation was found as 0.84 and 0.81, respectively, and can be considered as a very good match (Moriasi et al. 2007).

Table 4 Calibrated value and range of parameters of TANK model
Full size table
Fig. 4
figure 4

Observed and simulated runoff from TANK model

Full size image

AWBM model

Similar to the TANK model, the AWBM has been set up in RRL toolkit. The model warming, calibration and validation of the model have been carried out for the periods of 1991–1994, 1995 to 2004 and 2005 to 2015, respectively. The calibration of the parameters of the AWBM was done initially by auto-calibration and then genetic algorithm to optimize the parameters. The calibrated values of different parameters of AWBM in RRL are presented in Table 5. The observed and computed runoff from the optimized AWBM are plotted and presented in Fig. 5 and found an acceptable match. The Nash–Sutcliffe efficiency of the model was worked out as 0.76 and 0.79, respectively, and can be considered as the good match on a daily scale.

Table 5 Calibrated value and range of parameters of AWBM
Full size table
Fig. 5
figure 5

Observed and simulated runoff from AWBM

Full size image

SWAT model

In the study, SWAT which is a semi-distributed physical model has been established using digital elevation model, land use and soil maps of Tandula catchment (Fig. 6). The ASTER DEM has been used for delineation of the Tandula watershed and 12 sub-watersheds in the basin. The land uses have been divided into five groups namely deciduous forest (FRSD), low density urban (URLD), scrub (RNGB), agriculture (RICE) and water body (WATR). The soil map of the study area has been derived from the state soil map of National Bureau of Soil Survey & Land Use Planning, Nagpur (India) prepared for Chhattisgarh state and literature survey (Tamgadge et al. 2002).

Fig. 6
figure 6

Land use, soil and SWAT set-up for Tandula catchment

Full size image

From the analysis, it has been found that deciduous forest covers nearly 60% catchment of Tandula reservoir and soil is mainly of loamy in nature. After setting up of the model and writing the default values of all the parameters, a simulation run of the model has been made and exported to SWAT-CUP application for sensitivity, calibration and validation.

The sensitivity analysis has been carried out using t-stat (larger absolute value) and P value (smaller absolute value). The results of this analysis suggested that SCS curve number (r_CN2), saturated hydraulic conductivity (sol_k), soil antecedent water content (sol_AWC), Manning’s N for main channel (ch_N2), base flow alpha factor (Alpha_BF), soil evaporation compensation factor (ESCO) and threshold depth of water in the shallow aquifer required for return flow to occur (GWQMN) are the most sensitive parameters for Tandula reservoir catchment. The test statistics of uncertainty analysis along with best-fit value and ranges of different sensitive parameters have been depicted in Table 6. The comparison of observed and simulated runoff during calibration and validation has been presented in Fig. 7; from the analysis, it has been found that Nash–Sutcliffe efficiency of SWAT model was worked out as 0.75 during calibration and 0.65 during validation.

Table 6 Results of sensitivity, calibration and validation of SWAT model
Full size table
Fig. 7
figure 7

Observed and simulated from SWAT model

Full size image

In the study, two conceptual (AWBM and TANK) and a physical semi-distributed (SWAT) models were applied in a basin. These models contain a sperate set of parameters and optimization technique. The performance of these models was evaluated on the basis of some standard goodness-of-fit criterions including root-mean-square error, the coefficient of correlation, Nash–Sutcliffe efficiency and coefficient of determination, etc. The best-fit criterions for calibration and validation of different models are presented in Table 7.

Table 7 Goodness-of-fit criterions during calibration and validation of different models
Full size table

The efficiency criteria of different models during calibration and validation indicated a satisfactory performance of all these models used in the study. From the analysis, it has been found that RRL TANK model performed comparatively better in both calibration and validation, while SWAT model due to its complexity, multiple spatially distributed information and climatic data performed with the lowest efficiency. As SWAT model has several parameters to depict hydrological processes above and below the earth, sometime could not be optimized and gave less efficiency. However, due to incorporation of land use, slope, soil and climatic data, the SWAT model can be used for impact assessment of land use change and climate change assessment in a basin.

Conclusions

The multi models’ approach is preferred in hydrological modelling due to inherent multiple uncertainties in processes, input, output, etc. In the present study, two conceptual and one physically semi-distributed model have been applied in a basin where runoff data were determined by the water balance of the reservoir. The analysis suggested that the RRL TANK model performed better than the AWBM and the SWAT model used in the analysis. The performance of SWAT model is the lowest among all the models used in the study; however, use of spatially distributed information of landforms, soil, topography and climate data make this model capable of assessing the impact of land use, climate change and management practices applied in the basin. The model set-up of the conceptual model is easy in RRL, whereas SWAT model requires more spatial data and computational time. The model set-up in the conceptual model is limited to the single basin and single outlet; however, modelling in SWAT can be done with multiple sub-watersheds and outlets in a basin. The TANK model performs slightly better than AWBM ; however, calibration and validation of this model took more time and effort due to a large number of parameters.