Introduction

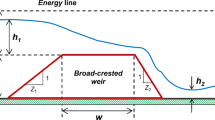
To control and maintain the flow in a channel or river, some discharge control structures such as side weirs are utilized. A side weir is built on the side of a main channel, and free spatially varying flow with decreasing discharge is the dominant regime over this hydraulic structure. Water is deviated from the main flow and sent to the side weir. Decreasing the ultimate (downstream) discharge in the main channel is the result of this action. It means if a flow with discharge (Q1) crosses a side weir, its discharge will be reduced (Q2) because of overspilling (Qw) (see Fig. 1). Inadequate assessment of a discharge coefficient and inappropriate hydraulic design of the structure may result in downstream damage or reduction in flow transmission capacity in the main channel.

Fig. 1
figure 1

General scheme of a TSCSW: (a) longitudinal section, (b) plan view and (c) cross-sectional view

Full size image

The hydraulic behavior of side weirs has received considerable interest by many researchers. Hager (1987), Swamee et al. (1994), Borghei et al. (1999), Muslu (2002) and Torabi and Shafieefar (2015) investigated the hydraulic and geometric characteristics of side weir hydraulic structures. Coşar and Agaccioglu (2004) investigated the discharge coefficient for a triangular side weir on a curved channel. The results showed that for a curved channel, the path of maximum velocity and the secondary current created by the bend both cause a much greater deviation angle toward the side weir. Also triangular side weir discharge coefficients along the bend are greater than the values obtained in the straight channel. Venutelli (2008) proposed a method for reducing discharge coefficients for side weirs by repeating steps to solve the nonlinear flow equations. Hyung and Sop (2010) studied discharge coefficients of sharp-edge and broad-crested weirs using a De Marchi discharge coefficient. The results showed the impact of upstream Froude number and weir height on wide open channels.

Rahimpour et al. (2011) investigated flow passing over a trapezoidal sharp-edged crest using both numerical and experimental techniques. The results showed that the discharge coefficient in subcritical flow is related to the Froude number, weir sidewall slope, ratio of crest length over the upstream depth and weir height over upstream depth of the side weir. Aydin and Emiroglu (2013) studied the discharge coefficient of flow over a side labyrinth spillway and its relevant parameters utilizing a finite volume method. They investigated the effect of parameters such as upstream Froude number, the ratio of weir height to its width and sidewall slope of the labyrinth side weir.

More recently, Abdollahi et al. (2017) investigated flow passing over labyrinth side spillways with some flow guiding obstacles; they used OpenFOAM software for the calculations. The results showed that the maximum discharge will occur when obstacles are perpendicular to the flow and are placed downstream of the spillway.

Despite numerous studies on the trapezoidal side spillways and their geometric and hydraulic characteristics, there are few investigations on the parameters that affect their discharge coefficients. In this paper, the discharge coefficient and relevant parameters in trapezoidal side weirs with various crest lengths, heights and wall slopes are investigated numerically using FLOW-3D.

Mathematical background

Dimensional analysis

The discharge coefficient of a TSCSW is related to geometric and hydraulic characteristics of the side weir and the fluid, respectively. Thus, we can write:

$$C_{d} = f_{1} \left( {y_{1} ,y_{2} ,\,V_{1} ,\,V_{2} ,P,L,B,g,T,Z,H,L^{\prime}} \right),$$
(1)

which can be rewritten using Buckingham’s Π theory:

$$C_{d} = f_{2} \left( {{\text{Fr}}_{1} ,\text{Re} ,{\text{We}},\frac{{y_{2} }}{{y_{1} }},\frac{{V_{2} }}{{V_{1} }},\frac{P}{{y_{1} }},\frac{B}{{y_{1} }},\frac{T}{L},\frac{H}{{L^{\prime}}},S_{0} ,Z} \right).$$
(2)

Here, Fr1 is the upstream Froude number, Re is the Reynolds number, We is the Weber number, P is the weir height, L is the side weir crest length, B is the main channel width, y1 and y2 are flow depths upstream and downstream, respectively, V1 and V2 are velocities upstream and downstream, respectively, Z is the sidewall slope, H is the main channel height, L’ is the main channel length, S0 is the channel bed slope, and T is the flow-passing width which equals T = L + 2zy. These dimensions and the physical situation are shown in a series of illustrations provided in Fig. 1.

The Reynolds and Weber numbers indicate the effects of viscosity and surface tension, respectively. The minimum depth of flow over the weir exceeds 3 cm, and the effect of surface tension can be neglected. In addition, the boundary layer is considered to be negligible and the viscosity effects are neglected. Also, the main channel width, length, height and longitudinal slope are constant and the ratios of y2/y1 and V2/V1 are small. Consequently, the impact of parameters of B, L’, H, S0, y2/y1 and V2/V1 is negligible. Finally, the following dimensionless parameters are expected to significantly affect the flow discharge coefficient:

$$C_{d} = f_{3} \left( {{\text{Fr}}_{1} ,\,\frac{P}{{y_{1} }},\frac{T}{L},Z} \right).$$
(3)

Continuity equations, momentum and free surface

The dynamic behavior can be described by a set of equations known as the St. Venant equations (Daneshfaraz and Kaya 2008; Norouzi et al. 2019). FLOW-3D is used to solve complicated fluid dynamics problems; it is able to model a wide range of fluid flows. This software can be used to model 3D unsteady free surface flows with complicated geometry in which the volume of fraction (VOF) method is utilized. The governing equations are the Navier–Stokes (Daneshfaraz et al. 2019; Ghaderi and Abbasi 2019) and continuity equations. The general form of the continuity equation is:

$$V_{F} \frac{\partial \rho }{\partial t} + \frac{\partial }{\partial x}(\rho uA_{x} ) + R\frac{\partial }{\partial y}(\rho vA_{y} ) + \frac{\partial }{\partial z}(\rho wA_{z} ) + \xi \frac{{\rho uA_{x} }}{x} = R_{\text{DIF}} + R_{\text{SOR}} .$$
(4)

Here, VF is the free volume coefficient; \(\rho\) is density and R is the source term. The general forms of the 3D momentum equations are:

$$\frac{\partial u}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial u}{\partial x} + vA_{y} \frac{\partial u}{\partial y} + wA_{z} \frac{\partial u}{\partial z}} \right] - \xi \frac{{A_{y} v^{2} }}{{xV_{F} }} = - \frac{1}{\rho }\frac{\partial P}{\partial x} + G_{x} + f_{x} - \frac{{R_{\text{SOR}} }}{{\rho V_{F} }}(u - u_{w} - \delta u_{s} )$$
(5)
$$\frac{\partial v}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial v}{\partial x} + vA_{y} \frac{\partial v}{\partial y} + wA_{z} \frac{\partial v}{\partial z}} \right] + \xi \frac{{A_{y} uv}}{{xV_{F} }} = - \frac{1}{\rho }\left( {R\frac{\partial P}{\partial y}} \right) + G_{y} + f_{y} - \frac{{R_{\text{SOR}} }}{{\rho_{{}} V_{F} }}(v - v_{w} - \delta v_{s} )$$
(6)
$$\frac{\partial w}{\partial t} + \frac{1}{{V_{F} }}\left[ {uA_{x} \frac{\partial w}{\partial x} + vA_{y} \frac{\partial w}{\partial y} + wA_{z} \frac{\partial w}{\partial z}} \right] = - \frac{1}{\rho }\frac{\partial P}{\partial z} + G_{z} + f_{z} - \frac{{R_{\text{SOR}} }}{{\rho V_{F} }}(w - w_{w} - \delta w_{s} )$$
(7)

In the above equations, P is pressure; Gx, Gy and Gz are volumetric accelerations; and fx, fy and fz are the mass accelerations. In FLOW-3D, unlike some numerical software such as HEC-RAS, the free surface profile is estimated using F(x, y, z) (Ghaderi et al. 2019). This function shows the fluid volume in the cell and is expressed as:

$$\frac{\partial F}{\partial t} + \frac{1}{{V_{F} }}\left[ {\frac{\partial }{\partial x}(FA_{x} u) + \frac{\partial }{\partial y}(FA_{y} v) + \frac{\partial }{\partial z}(FA_{z} w)} \right] = 0.$$
(8)

In the above equation, A is the average ratio of flow area along x-, y- and z-directions, u, v, w are average velocities along x, y, z and F is the fluid ratio function which takes on values between 0 and 1. If F = 0, the cell is completely full of air, and if F = 1, the cell is full of water. The free surface occurs where F = 0.5 (Daneshfaraz et al. 2016a).

Turbulence model

The RNG k–ε (Renormalized Group) turbulence model is used to simulate the flow domain because of its acceptable accuracy and success in prior studies (Aydin and Emiroglu 2013; Azimi and Shabanlou 2018; Daneshfaraz and Ghaderi 2017; Daneshfaraz et al. 2016b). The RNG k–ε model is a two-equation model that is expressed as:

$$\frac{\partial }{\partial t}(\rho k) + \frac{{\partial (\rho ku_{i} )}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{k} \mu_{\text{eff}} \frac{\partial k}{{\partial x_{j} }}} \right) + G_{k} + G_{b} - \rho \varepsilon - Y_{M} + S_{k}$$
(9)
$$\frac{\partial }{\partial t}(\rho \varepsilon ) + \frac{{\partial (\rho \varepsilon u_{i} )}}{{\partial x_{i} }} = \frac{\partial }{{\partial x_{j} }}\left( {\alpha_{s} \mu_{\text{eff}} \frac{\partial k}{\partial x}} \right) + C_{1s} - \frac{\varepsilon }{k}(G_{k} + G_{3s} G_{b} ) + C_{2\varepsilon } \rho \frac{{\varepsilon^{2} }}{k} - R_{\varepsilon } + S_{\varepsilon }$$
(10)

In these equations, k is the turbulent kinetic energy; \(\varepsilon\) is the turbulence dissipation rate, Gk is production of turbulent kinetic energy due to velocity gradient, Gb is turbulent kinetic energy production from buoyancy and YM is turbulence dilation oscillation distribution (Yakhot et al. 1992; Lai and Wu 2019). In the above equations, \(\alpha_{k}\) = \(\alpha_{s}\) = 1.39, \(C1s\) = 1.42 and \(C_{2\varepsilon }\) = 1.6 are model constants. The terms \(Sk\) and \(S_{\varepsilon }\) are sources terms for k and \(\varepsilon\), respectively. Turbulence viscosity \(\mu_{t}\) is defined using the following equations. In fact, the turbulent viscosity is added to the molecular viscosity to obtain, μeff, effective viscosity. It accounts for both molecular and turbulent effects. The following equations provide detail on how the effective viscosity is determined.

$$d\left( {\frac{{\rho^{2} k}}{{\sqrt {\varepsilon \mu } }}} \right) = 1.72\frac{\nu }{{\sqrt {\nu^{3} - 1 + C_{\nu } } }},$$
(11)
$$\nu = \mu_{\text{eff}} /\mu ,C_{\nu } = 100.$$
(12)

Methods and materials

Geometric model

In the present study, three crest lengths of 15, 20 and 30 cm with heights of 20, 30 and 40 cm and sidewall slopes of z = 1 and z = 2 are utilized to simulate the hydraulic and geometric characteristics affecting the discharge coefficient. The results of case L/B = 0.667, P = 40 cm and z = 1 are validated with the experimental results of (Tabrizi et al. 2015). The experiments were conducted in a rectangular flume with the length, width, and depth of 20, 0.6, and 0.6 m, respectively. The flume is made of 0.02-m-thick plexiglass with a bed slope of 0.001. With used plexiglass, the influence of sidewall effects is considered to be negligible based upon studying with Moradinejad et al. (2019). Table 1 shows the hydraulic and geometric conditions of the present study.

Table 1 Geometric parameters of the present study
Full size table

Solution domain characteristics and boundary conditions

Several computational meshes were utilized to select the appropriate mesh. As listed in Table 2, a comparison between the calculated and measured free surface profiles was performed. Based on this mesh refinement study, a computational mesh with 1,987,703 elements was selected for further calculations; the selected appropriate mesh results in a relative error, RMSE and maximum aspect ratio of 8.73%, 0.38 and 1, respectively. The same mesh was utilized to all models of this research.

Table 2 Mesh sensitivity analysis for the present study
Full size table

A symmetry (S) boundary condition was used for the upper boundary; specific discharge (Q) was used for the input flow and outlet (O) conditions for flow for the downstream boundary. Wall (W) boundary conditions were assigned for the bed and the sidewalls to enforce a no-slip condition. Figure 2 shows annotations of the applied boundary conditions of the TSCSW on the FLOW-3D model domain.

Fig. 2
figure 2

Boundary condition labels for the TSCSW model

Full size image

Results and discussion

Verification of numerical model and laboratory results

To validate the model, a comparison is made between the calculated and experimental results. In order to quantify the error, Eq. 13 was used. The simulation was completed in a sufficient duration to ensure steady conditions were achieved, and then, the comparison was made. This method is similar to that of (Zahabi et al. 2018):

$$E = \left| {\frac{{(Cd_{E} - Cd_{N} )}}{{Cd_{E} }}} \right| \times 100.$$
(13)

The term E is the relative error percentage, CdE is the experimental discharge coefficient and CdN is the numerical counterpart. Figure 3 and Table 3 show discharge coefficients and errors. Good agreement is found between the numerical and experimental data, and the experimental and numerical data represent a nearly similar trend.

Fig. 3
figure 3

Comparison of numerical and experimental discharge coefficients (P = 40 cm, L/B = 0.667, Z = 1)

Full size image
Table 3 Comparison of numerical and experimental discharge coefficients (P = 40 cm, L/B = 0.667, Z = 1)
Full size table

It can be seen that the largest difference between the data relates to P/y1= 0.743 (side weir height over the depth of upstream flow) and is equal to 7.13%.

Free surface profile flow over a TSCSW

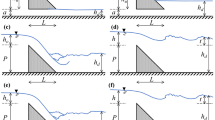
Figure 4 shows the flow passing over a TSCSW with a height of 20 cm. It is seen that the flow is spatially varied and the depth of flow reduces as a part of flow abandons the main channel. Also, the flow passing adjacent to the sidewall collides with the wall at an angle before returning to the main stream. As a result, an increase in the depth of the main channel can be observed.

Fig. 4
figure 4

Flow passing over a TSCSW with P = 20 cm

Full size image

Figure 5 shows the free surface profile of flow passing over a TSCSW for three different ratios of P/B. It can be seen that for various values of P/B, the water surface profile experiences a reduction and later re-enhancement in depth, which is caused by the flow passing to the side channel. By increasing the weir’s height, a secondary current will be created that reduces the water surface fluctuation and the flow surface profile experiences less curvature.

Fig. 5
figure 5

Free surface profile of flow passing over a TSCSW (P/B = 1.33, 1 and 0.667)

Full size image

Side weir length (L) effects

Figure 6 shows discharge coefficients for a TSCSW with P/y1 for different heights of P = 20, 30 and 40 cm. It is seen that there is very little trend in the results, in general, for any particular dataset. A slight decline is observed for P/B = 1 and L/B = 0.5 case, while a slight increase is found for P/B = 1.33 and L/B = 1.

Fig. 6
figure 6

Variation in discharge coefficient with P/y1 (weir height to upstream depth) (P/B = 1.33, 1 and 0.667)

Full size image

On the other hand, there is a notable spread that separates the individual datasets. It is evident as the weir’s length increases, for constant values of P/y1, the value of Cd increases. With increasing P/y1, the discharge coefficient of the TSCSW for L = 15 cm decreases. This length provides the shortest crest. This reduction in discharge coefficient is in accordance with findings of (Agaccioglu and Yuksel 1998; Emiroglu et al. 2010) who carried out research on rectangular sharp-edged side weirs with L/B = 0.5. However, for side weirs with a crest length of L = 20 cm, the discharge coefficient is almost constant, while it increases for L = 30 cm. The intensity of secondary flow and deviating flow from the main channel increases the discharge coefficient and crest length.

Effects of passing flow width (T)

Figure 7 shows the variation in discharge coefficient Cd in TSCSW and T/L (passing flow width over weir crest length) for weir heights of P = 20, 30 and 40 cm and 21 < T<32 cm.

Fig. 7
figure 7

Variation in Cd with T/L (passing flow width to weir crest length) in z = 1 (P/B = 1.33, 1 and 0.667)

Full size image

It is seen that increasing the weir height at constant T/L will increase the discharge coefficient. With increasing T/L for L/B values of 0.5 and 1, the discharge coefficient exhibits a decreasing trend in all three models and results in a weir crest length reduction.

Effects of upstream Froude number (Fr1)

Figure 8 shows variations in discharge coefficient Cd with upstream Froude number (Fr1) for different values of P/y1.

Fig. 8
figure 8

Variations in Cd (discharge coefficient) with upstream Froude number (Fr1) (L = 15, 20 and 30 cm)

Full size image

It is seen that the discharge coefficient increases with increasing P/y1 ratio and the weir crest length. This is due to increased weir height and to the reduction in the secondary current from the main channel to the side weir. The lower the height of the weir, the larger the return flow and the earlier the submergence of side weir occurs. Also, for constant values of P/y1, increasing the crest length will reduce the influence of the deviated flow and will increase the discharge of the side weir passing flow.

Sidewall slope of TSCSW (Z)

Figure 9 shows the variation in discharge coefficient with P/y1 and T/L ratios for two different sidewall slopes. It can be observed that different ratios of T/L and P/y1 and increasing the sidewall slope increase the discharge coefficient. Increasing the ratios of T/L and P/y1 at two sidewall slopes of TSCSW causes a decrease in the discharge coefficient. However, there are variations among discharge coefficients at two sidewall slopes. Some equations are proposed in Table 4 that can be used to estimate the discharge coefficient for different values in the slopes.

Fig. 9
figure 9

Variations in discharge coefficient with P/y1 and T/L for two different sidewall slopes (P/B = 1.33, Z = 1, 2)

Full size image
Table 4 Proposed equations for discharge coefficients for various sidewall slopes
Full size table

The 80–20 rule is utilized in proposing the above equations. With this approach, the coefficients and powers are derived using 80% of the data and the other 20% are used to validate the coefficients and powers. The relative error and the RMSE are calculated for that 20% of the data. Table 5 and Fig. 10 show the sensitivity analysis and numerical data variations with estimated data from the primary proposed equation (Eq. 3). According to Table 5, it can be seen that the T/L parameter has the greatest effect on discharge coefficient. Also, P/y1 has the largest effect on increases in the discharge coefficient. According to Fig. 10, it is seen that there is a good agreement among the numerical and estimated data.

Table 5 Sensitivity analysis for the general equation of discharge coefficient
Full size table
Fig. 10
figure 10

Variations in numerical data with estimates from (main equation, Eq. 3) for the TSESW model

Full size image

From the results that have been presented, some clear conclusions can be drawn.

  1. 1.

    The profile of flow passing through the TSCSW at different ratios of P/B first experiences a reduction at the beginning and then slightly increases further downstream. The reason for the reduction is due to flow separation caused by fluid entering the TSCSW. With increasing height of the weir, the water level alteration decreases and the flow surface profile experiences less curvature.

  2. 2.

    For constant ratios of P/y1, the discharge coefficient increases with increasing the crest length. Also, with increasing values of P/y1, the discharge coefficient for the TSCSW with a crest length of L = 15 cm is descending. On the other hand, the discharge coefficient is almost constant for L = 20 cm and increases for L = 30 cm. The reason for the increase is the intensity of secondary flow and the flow diverting from the main channel.

  3. 3.

    For constant ratios of T/L, the discharge coefficient is decreases for L/B = 0.5 and 1 in all three models, which means the crest length could be reduced.

  4. 4.

    With increasing Froude number upstream of a large crested TSCSW, the deviation of flow and the kinetic energy of the flow through the side weir increase. For side weirs with smaller crest lengths, the discharge coefficient at high Froude numbers decreases because of rapid submergence of the weir.

  5. 5.

    Sidewall slope increments will increase the discharge coefficient. This is due to the increase in the deviation angle and the kinetic energy.

  6. 6.

    Some dimensionless equations were proposed to estimate the variations in discharge coefficient of TSCSW with P/y1, T/L and Fr1.

  7. 7.

    Sensitivity analysis of the main discharge coefficient equation was performed, and this analysis showed that changes to T/L and P/y1 have the greatest impact on discharge coefficient.

Conclusion

In the present study, the discharge coefficient of trapezoidal sharp-edged side weirs (TSCSW) and their affecting parameters are investigated using FLOW-3D. In this research, three trapezoidal sharp-edged weirs with crest lengths of 15, 20 and 30 cm, heights of 20, 30 and 40 cm and sidewall slopes of Z = 1 and 2 are utilized. The numerical model was first compared with experimental results to demonstrate the suitability of the calculations for adequately capturing the flow features.

Subsequently, changes to numerous independent parameters were made using the computational software to determine their effect on the flow. Changes included modifications to the P/B ratio, P/y1, crest length, T/L, Froude number and slopes. New correlating equations are provided that allow the prediction of discharge coefficients for various values of the influencing parameters.