Introduction

When an abrupt change occurs in flow depth and/or velocity, the shocks or bores will appear. The shocks normally appear in supercritical flows, while transition from super- to the subcritical regime, named trans-critical, can produce a shock (i.e., hydraulic jump). They are divided into two general categories: dynamic shocks whose characteristics are various over time (i.e., produced shock due to dam break and gate operations) and static shocks whose locations and other characters are permanent after the flow steady state (i.e., hydraulic jump or oblique stock in transition).

The governing equations on shock simulation problem are the shallow flow equations. According to their nonlinearity, the analytical solution is limited to simplified cases such as reflectance of some important terms; hence, the numerical methods perform as valuable tools to solve the nonlinear shallow flow equations although, on the other hand, due to sudden changes in flow patterns by shock adjacent, the simulation of their locations and their shapes are more complicated. Therefore, the conventional numerical methods such as Preissmann (or four-point scheme) (Fennema and Chaudhry 1990) are not capable of capturing shocks. According to the solution known as the Euler equation, Jameson suggests ‘artificial viscosity’ and ‘modified equations’ to eliminate spurious non-physical oscillations adjacent sharp discontinuities (Jameson et al. 1981). Consequently, such methods were applied to shallow flow equations. In 1985, Fenema and Chaudhry applied beam–warming, Gabutti and Mc Cormack schemes including artificial viscosity for the simulation of the dam-break problem (Fennema and Chaudhry 1990).

Since the early days of the 1980s, the idea of Godunov conservative method has been in application for the solution of Euler equation. These methods are not capable of capturing sharp discontinuities such as shock and bores without employing numerical viscosity or simplifications of governing equations. In order to eliminate non-physical spurious oscillations, the ‘total variation diminishing (TVD) methods’ developed by Sweby (1984) and subsequently many researchers applied these methods to the solution of shallow flows in the 1990s. Alcrudo and Garcia-Navarro (1993) applied the Godunov-type finite volume method for the solution of shallow flow equations. Zhao et al. (1996) used the approximate Riemann solvers of Osher and Solomon for the simulation of unsteady flow in rivers. Chippada et al. (1998) continued with the Roe scheme to the modeling of flow through transitions and tidal waves. Also, Yang and Greimann (2000) went on to apply the TVD version of Roe scheme for the simulation of the dam-break problem with sediment transport. Zoppou and Roberts (2003) employed weighed average flux (WAF) in dam-break problem. Tseng et al. (2001) used high-resolution conservative methods for the simulation of wave in channels. Calleffi et al. (2003) applied approximate Riemann solver of HLL for the simulation of extreme floods in rivers. Sheng Bi et al. (2015) applied improved unstructured finite volume algorithm in 2D shallow flow modeling. Martins et al. (2017) offered a detailed validation of finite volume (FV) flood models in the case where horizontal floodplain flow is affected by sewer surcharge flow via a manhole.

In this research, the approximate Riemann solver of Roe, a TVD type scheme, has been applied for simulations of the steady oblique shocks caused by the confrontation of a supercritical flow to cross-barrier in the open-channel flow. In this line of attack, several laboratory experiments were used.

The governing equation

Shallow water equations are derived by the depth averaging of the three-dimensional Navier–Stokes equations, considering a hydrostatic pressure distribution and incompressible flow. These equations may be applied for studying many physical phenomena such as dam-break problem, open-channel flow, flood waves, acting forces on shoreline structures and solute transport. The governing equations, based on the conservation of mass and momentum, for the two-dimensional unsteady flow in a rectangular channel, may be expressed as (Zoppou and Roberts 2003):

$$\frac{{\partial \varvec{U}}}{\partial t} + \frac{{\partial \varvec{F}(\varvec{U})}}{\partial x} + \frac{{\partial \varvec{G}(\varvec{U})}}{\partial y} = \varvec{S}(\varvec{U}).$$
(1)

In Eq. (1), U is the vector of the conserved variables, F(U) and G(U) are the flux vectors in the x and y directions, respectively, and S(U) is the vector of source terms. The expanded form of the vectors may be written as:

$$U = \left[ {\begin{array}{*{20}c} h \\ {hu} \\ {hv} \\ \end{array} } \right]$$
(2)
$$F(U) = \left[ {\begin{array}{*{20}c} {hu} \\ {hu^{2} + 0.5gh^{2} } \\ {huv} \\ \end{array} } \right];\quad \varvec{G}(\varvec{U}) = \left[ {\begin{array}{*{20}c} {hv} \\ {huv} \\ {hv^{2} + 0.5gh^{2} } \\ \end{array} } \right]$$
(3)
$$\varvec{S}(\varvec{U}) = \left[ {\begin{array}{*{20}c} {S_{1} } \\ {S_{2} } \\ {S_{3} } \\ \end{array} } \right].$$
(4)

In Eqs. (2) and (3), h is water depth and u(v) is flow velocity in the x(y) direction. In traditional shallow flow modeling, with the negligence of many physical phenomena such as acting body forces, wind stresses, evaporation and infiltration, tide potential, and considering only the effects of bottom slope and friction in the x and y directions, the source term variables may be written as:

$$\varvec{S}(\varvec{U}) = \left[ {\begin{array}{*{20}c} 0 \\ {gh(s_{ox} - s_{fx} )} \\ {gh(s_{oy} - s_{fy} )} \\ \end{array} } \right]$$
(5)

In Eq. (5), sox and soy are the bottom slopes and Sfx and Sfy stand for the friction slope in the x and y directions, which may be estimated from the Manning equation as:

$$S_{fy} = \frac{{vn^{2} \sqrt {u^{2} + v^{2} } }}{{h^{4/3} }}\quad S_{fx} = \frac{{un^{2} \sqrt {u^{2} + v^{2} } }}{{h^{4/3} }}$$
(6)

where n is the coefficient of Manning roughness.

Numerical modeling

The differential form of conservation laws shows the capability of flow simulation in smooth regions. In discontinuous regions, however, an integral form of governing shallow flow equation may be applied including the weak solutions as well. Integration of Eq. (1) for a computational cell (i, n) in the x-t plane leads to a general conservative formula may be written as Eq. (7), considering the source terms:

$$\varvec{U}_{i}^{n + 1} = \varvec{U}_{i}^{n} - \frac{\Delta t}{\Delta x}\left[ {\varvec{F}_{i + 1/2}^{n} - \varvec{F}_{i - 1/2}^{n} } \right] + \Delta t\;\varvec{S}_{i}^{n}$$
(7)

where superscript n denotes computing time level, ∆t is the time step, and ∆x is the cell width. Fi−1/2 and Fi+1/2 stand for input and output numerical fluxes to the computational cell (i), respectively (Zoppou and Roberts 2003).

Riemann solvers

Riemann problem is defined as an initial value problem. The Riemann solvers in conservative methods are divided into four main groups: (1) flux difference splitting methods, (2) flux vector splitting methods, (3) exact Riemann solvers and (4) approximate Riemann solvers (Le Veque 1997). The approximate Riemann solvers on finite volume frameworks are also known as ‘high-resolution finite volume methods.’ In FDS methods, since the shallow flow equations system is from the parabolic type and includes the inherent character of signal propagation, numerical fluxes are derived based on local information of wave propagation. To this extent, they have special capability for capturing the sharp discontinuities. The FDS methods are derived based on Godunov method. Therefore, they are known as ‘Godunov-type’ methods.

The Roe scheme

The numerical fluxes in Roe scheme have been derived explicitly on the basis of upwinding technique (Glaister 1988):

$$+ 0.5\sum\limits_{k = 1}^{3} {\varPhi (\tilde{r}_{i \pm 1/2}^{k} )\tilde{\alpha }_{i \pm 1/2}^{k} } \left| {\tilde{\lambda }_{i \pm 1/2}^{k} } \right|\left( {1 - \frac{\Delta t}{\Delta x}\left| {\tilde{\lambda }_{i \pm 1/2}^{k} } \right|} \right)\tilde{R}_{i \pm 1/2}^{k} F_{i \pm 1/2}^{Roe - TVD} = 0.5\left( {F_{i} + F_{i \pm 1} } \right) - 0.5\sum\limits_{k = 1}^{3} {\tilde{\alpha }_{i \pm 1/2}^{k} \left| {\tilde{\lambda }_{i \pm 1/2}^{k} } \right|\tilde{R}_{i \pm 1/2}^{k} }$$
(8)

where

$${\tilde{\mathbf{r}}}_{{i + {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} = \frac{{\tilde{\alpha }_{{_{{_{{i + 1/2 - \text{sgn} (\lambda {\kern 1pt}_{i + 1/2} )}} }} }} }}{{\tilde{\alpha }_{i + 1/2} }}$$
(9)

In Eq. (8), Φ(r) is a limiter function; for Φ(r) = 0, there will be an upwind first-order TVD scheme, and for Φ(r) = 1, the Lax–Wendroff second-order non-TVD scheme will come out.

In order to eliminate the spurious oscillations that occur in the adjacent of sharp gradients, any of the limiter functions may be used. Thus, a second-order TVD scheme, or the so-called Roe scheme, will be achieved.

The limiter functions are divided into two main categories: the flux limiters and the slope limiters. The Superbee is one of the flux limiters (Eq. 10), and the Minmod is the slope limiter function (Eq. 11):

$$\varphi (r) = \hbox{max} \left[ {o,\hbox{min} (2r,1),{\text{mir}}(r,2)} \right]$$
(10)
$$\varphi (r) = \hbox{min} \bmod (1,r).$$
(11)

The other components of Eqs. (10–11) are specified as follows:


λ: eigenvalue of Jacobian flux vector \((A = \frac{\partial F}{\partial U})\), R: right eigenvector of matrix A and α: wave strength or Roe coefficient that might be estimated by the following (Toro 2001):

$$\tilde{\alpha }_{i + 1/2,j}^{1,3} = \frac{1}{2}\Delta h \pm \frac{1}{2c}\left\{ {\Delta (uh) - u.\Delta h} \right\}$$
(12)
$$\tilde{\alpha }_{i + 1/2,j}^{2} = \Delta (vh) - v.\Delta h.$$
(13)

Extension to 2D problems

Numerical computation of the two-dimensional equations may be carried out by two augmented one-dimensional operators, which are applied successively in the x and y directions. For example, one can write (1) in two augmented one-dimensional equations with an ordinary differential equation as:

$$U_{t} + F_{x} (U) = S_{x} (U)$$
(14)
$$U_{t} + G_{y} (U) = S_{y} (U).$$
(15)

At first, one can solve Eq. (14) with the initial condition, and next the outcome state variables are considered as initial data and Eq. (15) is solved. The results are the variable in the new time step. This process is of the first-order accuracy. The second-order accuracy can be realized by computation of fluxes from Eqs. (14) and (15) via 0.5Δt, and then, the following process will be accomplished (Toro 2001):

$$U_{i,j}^{n + 1} = L_{y} \left( {\frac{\Delta t}{2}} \right)\;L_{x} \left( {\frac{\Delta t}{2}} \right)\;L_{x} \left( {\frac{\Delta t}{2}} \right)\;L_{y} \left( {\frac{\Delta t}{2}} \right)\;U_{i,j}^{n} \;.$$
(16)

In Eq. (7), (\(F_{i \pm 1/2,j}\)) and \((G_{i,j \pm 1/2} )\) are numerical fluxes that may be replaced by Eq. (8), and Sx and Sx are the source term vectors in x and y directions that may be replaced by the following equations:

$$S_{x} = \left( {\begin{array}{*{20}c} 0 \\ {gh(s_{0x} - s_{fx} )} \\ 0 \\ \end{array} } \right)$$
(17)
$$S_{y} = \left( {\begin{array}{*{20}c} 0 \\ 0 \\ {gh(s_{0y} - s_{fy} )} \\ \end{array} } \right).$$
(18)

The numerical experiments show that the first-order accuracy upwind scheme has dissipative behavior in a shock front. The second-order Lax–Wendroff scheme makes spurious oscillations in adjacent of sharp discontinuities. The TVD version of Roe scheme is capable of capturing sharp discontinuities as well as the smooth region (Alcrudo and Garcia-Navarro 1993).

Initial and boundary conditions

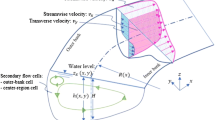
The initial conditions are the flow parameters at time t = 0. The boundary conditions are divided into two general categories of open and solid boundaries. For current simulation, which can be seen in Fig. 2, in the longitudinal channel walls there is a solid boundary as well as upward and downward of the barrier. On the other hand, due to the supercritical condition in the downstream end the boundary is fully open. In the upstream of modeling reach, there is an open boundary with one extra condition of constant discharge for subcritical flow regime.

Stability condition

In order to ensure the stability of the numerical scheme, the Courant–Friedrichs–Lewy (CFL) condition for the problems should be maintained all over the computational domain:

$$\Delta t = {\text{CFL}}\frac{\hbox{min} (\Delta x,\Delta y)}{{\hbox{max} \left[ {\left( {\left| u \right| + \sqrt {gh} } \right)\;,\;\left( {\left| v \right| + \sqrt {gh} } \right)} \right]}}$$
(19)

where for a stable solution 0 < CFL ≤ 1.0.

Application of the model

The presence of a cross-barrier partially in width of an open channel results in the increase in water depth in upstream (backwatering), then according to the flow releasing downstream beside of contraction and the increasing the velocity and make it as a supercritical flow. The lateral component of the velocity makes the flow hit to the channel wall, and it generates the oblique shocks that developed successively and decrease the sharpness and height to the downstream (Fig. 1).

Fig. 1
figure 1

The 3D view of a flume with cross-barrier

Full size image

In this research, the developed shocks in the mentioned case have been simulated in two dimensions with Roe TVD numerical scheme. The numerical results will be compared with some experimental data from a laboratory setup.

The modeling reach has a longitudinal length of L = 4 m that cross-barrier is located at Lu = 1 m from upstream of reach. Due to the importance of produced shocks at downstream, the simulation domain includes 1 m in upstream of barrier and 3 m in downstream. The boundary conditions are divided into groups of open and solid or wall boundary which are shown in Fig. 2. The flume width is B = 0.4 m with bed slope of S0 = 0.006625. The barrier lengths are in three cases Lb = 0.06 m, 0.12 m and 0.16 m, located in normal direction of flow, partially. The numerical modeling grid size is Δx = Δy = 0.02 m.

Fig. 2
figure 2

The boundary conditions in numerical modeling

Full size image

Figure 3 shows the 3D view and contour lines of flow depths that resulted from numerical simulation with a barrier length of 6 cm. In general, it can be seen that numerical modeling can simulate shock pattern in comparison with the experimental observation.

Fig. 3
figure 3

The 3D view and counter lines of depths resulted from numerical experiments

Full size image

Laboratory setup and measurements

In the present research, a laboratory flume located in hydraulic laboratory of the Ferdowsi University of Mashhad (Iran) has been used. The general view of the laboratory setup is shown in Fig. 4. The material of flume’s wall is the Perspex, and the bed is steel that Manning roughness is estimated to be n = 0.01 by some laboratory tests. The steel barrier with 3 mm thickness is located on the left channel wall normally in the flow direction (Fig. 5) and sealed well. When the pump is started, the flow gets stationary state within a few seconds and one can observe successive stationary and oblique shocks which appear in downstream of the barrier.

Fig. 4
figure 4

Experimental setup view

Full size image
Fig. 5
figure 5

Developments of stationary and oblique shocks in downstream of barrier

Full size image

The water depths have been measured in three longitudinal sections and 12 cross sections which are shown in Fig. 6 The measured flow depths data in longitudinal profiles are with increments of DX = 4 cm and latitudinal profiles with increments of DY = 2 cm. A scale with 1 mm error accuracy has been used.

Fig. 6
figure 6

The measured flow depths in longitudinal and cross sections

Full size image

Comparison between experimental and numerical results

In this section, Roe TVD scheme has been applied for 2D simulation of stationary oblique shocks which are developed in the mentioned case of a laboratorial flume. For the barrier length of L = 6 cm, the numerical results are compared with experimental measurements. The barrier length is L = 6 cm, which may be fixed in the left channel wall. In laboratorial experiments, the flow discharge has been measured by volumetric methods, and it is equal to Q = 42.5 l/s. The numerical results by employing the Roe TVD scheme in comparison with experimental measurements are shown in Figs. 7 and 8. As it is deduced from longitudinal and latitudinal profiles, the applied numerical method can capture the general developed stationary shock pattern. Some divergences in numerical results in comparison with the experimental flow depth data may be resulted from the following:

  1. 1.

    The relative error in measuring the depth and the flow discharge which is due to the extreme oscillation and turbulence of the flow, especially in the first downstream shock that includes a barrier.

  2. 2.

    Despite the fact that the actual thickness of the barrier is about 3 mm, in the numerical modeling it is considered equal to 0.02 m.

  3. 3.

    Although the flow condition is 3D around the barrier, 2D shallow water equations (averaged depth) are applied in the numerical model.

  4. 4.

    The applied numerical model includes a second-order accuracy. Although the previous experiments and also the latest results of this modeling show the capability of this numerical method to capture the shocks, applying more accurate equations will be more helpful.

  5. 5.

    The first step, which is created in the first downstream reflection (Sec 6 in Fig. 8), is produced from the extreme jet flow, which is faced to a wall. It should be mentioned that the present theoretical model is not able to simulate such flows.

Fig. 7
figure 7

The longitudinal profiles of flow depths in numerical and experimental results

Full size image
Fig. 8
figure 8

The latitudinal profiles of flow depths in numerical and experimental results

Full size image
Fig. 9
figure 9

The shock pattern in the first reflection of downstream of barrier

Full size image

Conclusions

The conservative methods based on Riemann solvers are capable of capturing shocks (Fig. 9). In this study, the approximate Riemann solver of Roe (TVD version) has been employed to study the shocks behavior which is produced by the attendance of a cross-barrier in supercritical open-channel flow. It is concluded that the applied numerical scheme is generally able to capture developed stationary shocks downstream of cross-barrier in the flume. Both measured data and numerical experiments show that the produced shocks are damping by faring from cross-barrier to downstream end. Due to the existence of flow conditions around the barrier, especially at its downstream, the flow pattern is three-dimensional; therefore, the two-dimensional numerical method is not able to capture shock height properly.