Prediction of the sliding type and critical factor of safety in homogeneous finite slopes

Abstract

In this paper, the effect of soil material parameters including soil specific weight (γ), cohesion (C), angle of internal friction ($\emptyset$), and geometric parameter of slope including angle with the horizontal (β) for a constant slope height (H) on factor of safety (F_s) was investigated. F_s was considered in two scenarios: (1) slope with dry condition, and (2) with steady-state saturated condition that comprises water level drawdown circumstances. In addition, the type of slip circle was also investigated. For this purpose, the SLOPE/W software as a subgroup of Geo-Studio software was implemented. Results showed that decreasing of water table level and omitting the hydrostatic pressure on the slope consequently would result in safety factor decrement. Comparison of the plane and circular failure surfaces showed that plane failure method produced good results for near-vertical slopes only. Determination of slip type showed that for state (30° < β < 45°), the three types of failure circles (toe, slope or midpoint circle) may occur. For state (45° < β < 60°), two modes of failure may occur: midpoint circle and toe circle. For state (β > 60°), the mode of failure circle is only toe circle. Linear and nonlinear regression equations were obtained for estimation of slope safety factor.

Introduction

Slopes failure is a natural phenomenon that occurs in many countries around the world. Due to the construction of roads and residential buildings on the slopes in different parts of the world, preservation stability of these slopes is considered necessary.

In general, the cause of the failure of the soil slope is mainly due to increase in the shear stress force at the surface of failure. In fact, stability calculations in the soil slopes are the comparison between driving forces (to cause slope instability) in creating failure and resisting forces respect to failure. The factor of safety represents the stability of a soil mass against potential failures (Das 2010). Different factors affect the stability of slopes. These parameters include soil cohesion, soil friction angle, existing stresses and water surface level. These parameters affect the shear resistance of the slip surface (Das 2010). Limit equilibrium method is one of the oldest methods for determining the critical slip surface and minimum factor of safety. Most methods for calculating slope stability are based on the principles of forces and moments balancing (Haji Azizi et al. 2015). In this method, the failure is assumed to occur at a certain failure surface. Therefore, the required shear stress to maintain the balance with the shear strength of the soils compared and the factor of safety of the slope is calculated. This process is performed for several different surfaces and a surface with minimum factor of safety, as the potential failure surface and its associated factor of safety is accepted as the answer to the problem. The mode of the failure surface is different depending on the type of slope constituent material and can be a plane, circular, curved or logarithmic or a combination of them. If the constituent materials are homogeneous, the failure surface will be close to the circle (Rahimi 2013). Thus, depending on the assumptions made, several methods have been developed that provide different factors of safety, among which these methods can be obtained using the Fellenius method (Fellenius 1927), the modified Bishop method (Bishop and Morgensrern 1960), the balance of the forces of Lowe and Karafiath (1960), the modified Janbu method (Janbu 1973), US Army Corps of Engineers method (1970), Spencer method (Spencer 1967), Morgenstern–Price method (Morgenstern and Price 1965) and Sarma’s method (Sarma 1973). Fellenius (1927) presented the first method of slices to study the stability of the soil slopes. In slices method, the slip surface is assumed as a circular arc and the soil mass on top of it is plotted along the lines of a series of parallel lines and the slip-resistant and active forces are calculated for each slice. At the end, the balance of force or moments is calculated and the factor of safety is calculated. In the original Fellenius method, the factor of safety is based on the balance of the moments and the force caused by the side pressure of the soil (horizontal and vertical components in each part) which is considered as zero. The simple Bishop method is based on the condition of the moments and, unlike the Fellenius method, the balance of forces in the vertical direction is also investigated, but in this case, the horizontal forces were eliminated on both sides of the slice (Bishop 1955). Based on the obtained experience, the accuracy of the simplified Bishop method is far more extensive than the Fellenius method, and the removal of lateral forces of the parts does not have much effect on the accuracy of the calculations and, in most cases, the error in the laboratory methods for assessing the soil specification is very precise and more accurate than the complex methods (Bishop 1955). According to Whitman and Bailey (1967), the error in simplified Bishop’s method was compared with the method that is more accurate and it was found to be maximum 7% and typically 2%. The method developed by Morgenstern and Price (1965) can examine the slope stability at all surfaces of failure (in any form) and calculate the factor of safety. In this method, not only tangential and normal forces, but also the moment balance for each slice is provided (Morgenstern 1963). Singh (1970) provided a graphical method for determining the factor of safety of stability of slopes, and the results showed that, for angles of 3 degrees ($\emptyset > 3^\circ )$, the critical slip circles are mostly toe circle. Spencer (1967) has provided a method for determine the factor of safety (F_s) by taking into account the inter slice forces, which does satisfy the equations of equilibrium with respect to moment and forces. The results of Spencer’s study have been developed by the charts. Michalowski (2002) presented a graphical method for studying the stability of simple slopes, which can provide a factor of safety directly with geometric properties and related materials. In this study, the surface of non-circular arc failure (logarithmic spiral) has been selected. Steward et al. (2011) studied the stability of different slopes in terms of geometry and materials using the SLOPE/W software. The result showed that the failure surface is mostly in the type toe circle, but in some cases they can also be in the type of midpoint circle, and finally a graphics is also used to determine the factor of safety without any trial-and-error method. Erzin and Cetin (2013) presented a method for prediction of the critical factor of safety on a homogeneous finite slope using artificial neural network (ANN) and multiple regression (MR) models. To achieve this, the F_s values of 675 homogenous finite slopes having different soil and slope parameters were calculated by using the simplified Bishop method and the minimum (critical) F_s value for each slope was determined and used in the ANN and MR models. The results obtained from ANN and MR models were compared with those obtained from the calculations. The values predicted from ANN models matched the calculated values much better than those obtained from MR models. Rotational failure mechanism of undrained clay slopes was analyzed by Gaopeng et al. (2014). Considering the influences of stiff stratum and overload conditions on the stability of slopes, stability charts for undrained clay slopes have been established with integrated parameters of stiff stratum depth, load value and slope angle. The stability coefficient of undrained clay slopes subjected to overload and stiff stratum depth can rapidly be obtain using the suggested charts; therefore, the safety factors of such slopes can be obtained with the known parameters. Moreover, the proposed charts also identify the types of rotational failure mechanisms associated with the stability coefficients (Gaopeng et al. 2014).

The main objective of this research is to investigate the effect of soil material parameters including soil specific weight ($\gamma$), cohesion (C), angle of internal friction ($\emptyset$) and geometric parameter of slope including angle with the horizontal ($\beta$) for a constant slope height on factor of safety (F_s) and presenting the relations to calculate the direct factor of safety. In this research, a complete dry and drainage mode was considered, and then, the impact of the water surface drawn down on the homogeneous slope is considered. In order to achieve this goal, SLOPE/W software (which is a sub-program of Geo-Studio, version 2012) is used. In this research, in order to predict of factor of safety of dry and saturated condition, different models by runs of SLOPE/W were made and the factor of safety of slopes was investigated. It should be noted that slopes simulations with saturated condition have been made by assuming steady-state condition.

Materials and methods

Equilibrium method

The software SLOPE/W is used to investigate the slope stability and to determine the factor of safety in the slope design. This practice is done in software through limit equilibrium methods (LEM) such as Bishop, Janbu or through other methods such as Morgenstern–Price and Spencer. In SLOPE/W software, unlike other subgroup of Geo-Studio, 2012 software, the finite element method is not used and includes a set of graphical and limit equilibrium methods for analyzing slope stability (Geo-Studio 2012). In general, various procedures of stability analysis may be classified into two groups: (1) mass procedure, and (2) method of slices. In case (1), the mass of the soil above the surface of sliding is taken as a unit although this is not the case in most of the natural slopes. This procedure is useful when the soil that forms the slope is assumed homogeneous. In case (2), the soil above the surface of sliding is divided into a number of vertical parallel slices and the stability of each slice is calculated separately. This is a popular technique in which the non-homogeneity of the soils and pore water pressure can be taken into consideration (Das 2010). The fundamentals of SLOPE/W software are based on the method of slices. In SLOPE/W, types of resistance models have been defined depending on the type of problem that can be used. In this study, for investigating stability of a slope, LEM is used. In this method, the factor of safety is equal to the ratio of soil resistance to shear stress and is necessary to set the critical in the LEM state (slip threshold) according to Eq. (1).

$$F_{\text{s}} = \frac{{C^{{\prime }} }}{{C_{m}^{{\prime }} }} = \frac{{\tan \emptyset^{{\prime }} }}{{\tan \emptyset_{m}^{{\prime }} }}$$

(1)

In Eq. (1), $C^{{\prime }}$ and $\emptyset^{{^{\prime } }}$, the shear strength parameters of the soil that are determined using the Mohr–Coulomb law resistance model, which is the most common method for expressing the shear strength of geotechnical materials. $C_{m}^{{\prime }}$ and $\emptyset_{m}^{\prime }$ are the required amount of shear strength parameters on the slip threshold.

Modeling setup

In this study, the soil specific weight ($\gamma$), cohesion (C), angle of internal friction ($\emptyset$) and angle with the horizontal ($\beta$) for slope height (H) were investigated as effective parameters on the factor of safety (F_s) on slope with dry condition and with steady-state saturated condition. In addition to the above-mentioned parameters, the water level parameter was used to study the effect of the water level drop on the factor of safety in the saturation soil.

Figure 1 shows the schematic representation of the simulated model and the studied parameters. In order to investigate the effect of each of the aforementioned factors, the SLOPE/W software was used on the stability of factor of safety. For numerical modeling, the number of each of the parameters was studied: Soil specific weight ($\gamma$), cohesion (C), angle of internal friction ($\emptyset$) and angle with horizontal ($\beta$) are 4, 4, 3 and 4, respectively, and in the end 192 models were simulated. It should be noted that the slope height in all models is considered constant (H = 8 m). In addition to simulation in the dry state, the effect of the water level drawdown (h) on the stability of the safety factor was also studied. The values of each of the parameters studied in this simulation are presented in Table 1.

Fig. 1

A schematic representation of the simulated model and the studied parameters

Table 1 The range of parameters studied in the numerical model of this study

Accuracy assessment measures

In this study, regression equations are presented for estimation of factor of safety, F_s. To assess the ability and accuracy of the regression equations, two statistical indicators including determination coefficient (R²) and root mean square error (RMSE) were used.

Results and discussion

Slope with dry condition

After simulating the critical slope in the software, the probable slip surface and the stability factor of safety in the critical conditions as well as the type of slippage can be observed. In Fig. 2a–c, if the specific weight ($\gamma$) of 15 kN/m³, cohesion (C) of 25 kN/m² and the angle of internal friction ($\emptyset$) of 14° is applied for slope angles ($\beta$) 30, 45, 60, respectively, the factor of safety after the simulation is obtained as 2.142, 1.912 and 1.622, respectively. As we can see, the change in the geometric shape of the slope causes a relative change in the resistant and destructive forces, and various degrees of stability factor of safety have arisen. As can be seen, the factor of safety has decreased with increasing slope angle, $\beta$. It should be noted that the SLOPE/W software calculates and draws up all potential slip circles to determine the factor of safety for the given condition, and considers the minimum possible value as the critical factor of safety.

Fig. 2

The factor of safety and the type of slip circle for the state. a $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\,\gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 30^\circ$, b $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\,\gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 45^\circ$, c $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\, \gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 60^\circ$

Figure 3a indicates changes in factor of safety (F_s) for all potential slip surfaces for estate $\emptyset = 14^\circ ,\;C = 25\,{\text{kN/m}}^{2} , \;\gamma = 15\,{\text{kN/m}}^{3} ,\;\beta = 30^\circ$, in which the value of the factor of safety against sliding (F_s) for critical slip surface is 2.142. The sliding wedge (above critical slip surface) for this condition is divided into 30 slices, and the information of the 12th slice is shown in Table 2. Also Fig. 3b provides the free-body diagram and force polygon for the 12th slice.

Fig. 3

Safety factor changes (F_s) for potential slip surfaces on the slope in the state of a $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\,\gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 30^\circ$. b Forces acting on the 12th slice and force polygon for equilibrium

Table 2 The information of the 12th slice for the state $\emptyset = 14^\circ , \,C = 25\,{\text{kN/m}}^{2} ,\, \gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 30^\circ$

Figure 4a, b shows the changes in the dimensionless parameter (F_s/$\tan \,\emptyset$) versus (C/$\gamma H\tan \emptyset$). By comparing Fig. 4a, b with constant internal friction angle condition $\emptyset = 14^{o}$, with increasing soil cohesion, the factor of safety increases and a direct (linear) relationship between the factor of safety and cohesion is established.

Fig. 4

The effect of slope materials on the factor of safety for the state. a $\emptyset = 14^\circ \,{\text{and}}\,C = 25\;{\text{kN/m}}^{2}$ and b $\emptyset = 14^\circ \,{\text{and}}\,C = 30\,{\text{kN/m}}^{2}$

Figure 5 provides change in relative factor of safety (F_s/m) with the slope angle (β). The stability number (m) is defined as $m = \frac{C}{\gamma H}$. From Fig. 5, it is clear that the factor of safety can be reduced by increasing the angle of slope to the horizon.

Fig. 5

Factor of safety change (F_s) versus slope angle (β) for the state ($C = 15\,{\text{kN/m}}^{2} ,\emptyset = 14^\circ ,18^\circ ,22^\circ$)

In engineering designs, in addition to knowing the factor of safety against sliding for the slope, it is important to have information about the mode of failure circle of finite slope. In general, the failure circle is referred to as toe circle if it passes through the toe of the slope and as a slope circle if it passes above the toe of the slope. Midpoint circle (base failure) occurs in such a way that the surface of sliding passes at some distance below the toe of the slope (Das 2010).

Figure 6 shows the boundaries of each mode of failure circle relative to the slope angle. Vertical axis is the occurrence percentage of each slip circle. For angles larger than 30 and less than 45 degree (30° < β < 45°), the three types of failure circles (toe, slope or midpoint circle) may occur. For angles larger than 45 and less than 60 (45° < β < 60°), two modes of failure may occur: midpoint circle and toe circle. For angles larger than 60 degrees ($\beta > 60^\circ$), the mode of failure circle is only toe circle.

Fig. 6

The boundaries of the potential slip circle slope relative to the slope angle

Figure 7 shows the variation of stability number (m) versus the factor of safety (F_s). As can be seen from the figure, with increasing the stability number, the factor of safety increases for a given slope angle. The advantage of Fig. 7 is that, with the presence of a stability number, value of safety of factor and the type of slip can also be determined simultaneously. For example, for a stability number 0.1 ($m = 0.1$) and a slope angle of 30 degrees ($\beta = 30^\circ$), the factor of safety is 1.6 ($F_{\text{s}} = 1.6$) and the mode of failure circle is slope circle.

Fig. 7

Classification of slip type for slope angle and different stability numbers

Figure 8 shows another variation of the slip factor of safety change in a non-dimensional manner. The use of dimensionless $m/\tan \emptyset$ and $\tan \emptyset$/F_s parameters produced a linear equation between effective parameters.

Fig. 8

Determination of the factor of safety against the stability number for different angles

In order to determine the factor of safety against slope stability, Michalowski (2002) performed a stability analysis of slopes using the kinematic approach of limit analysis to a rigid rotational collapse mechanism in which the failure surface in soil assumed an arc of a logarithmic spiral. Michalowski (2002) presented charts for determining factor of safety, F_s, by value of dimensionless parameters, $C/(\Gamma) (H) (tan-\phi)$, $F_{\text{s}} /\tan \emptyset$ and slope angles, $\beta$. In practice, the use of a chart requires interpolation and the use of a ruler that is time-consuming and is not accurate. In the present study, the necessary data ware extracted from Michalowski’s chart (2002), and then, the regression equation was developed to solve the interpolation problem. The result is a linear and a nonlinear equation according to Table 3. It is observed that the nonlinear equation presents the appropriate results, in which the root mean square error (RMSE) is less than linear equation and the determination coefficient (R²) is greater than the linear equation obtained. In the next step, we compared the proposed method with the SLOPE/W software output (Table 4).

Table 3 The regression equations extracted from the Michalowski (2002)

Table 4 Comparison of the present numerical method for F_s with Michalowski (2002)

In order to estimate the stability factor of safety with each of the Morgenstern–Price, Janbu, Bishop and Ordinary (Fellenius or Swedish circle) methods, linear regression equations were also extracted by using SPSS (SPSS, version 22 2015). The results of these calculations are shown in Table 5. It should be noted that these equations are obtained for the simulated range $30 < \beta < 75, 14 < \emptyset < 17, 22 < \gamma < 25 \,{\text{and }}\,15 < C < 25$.

Table 5 Regression equation to obtain the factor of safety of slopes

According to Table 5, it is noted that the proposed regression equations are highly accurate in estimating the safety factor of slope stability. The proposed equation for Janbu method has the highest accuracy with RMSE = 0.075 and R² = 0.969 (Table 5). Bishop’s method provides less accuracy than the other methods. But in Bishop’s method, maximum error is 1.36% and this can be ignored. In the research of Whitman and Bailey (1967), maximum error of F_s is 7% and mean error is 2%. Thus, Bishop’s simplified method can be used because of its simplicity and accuracy in the designs. In addition to the above criteria, in order to check the accuracy of the proposed regression equations, the data scatter diagram was used in Fig. 9a–d.

Fig. 9

The safety factor of the numerical and regression method, a Morgenstern–Price method, b Janbu method, c Bishop method and d ordinary method

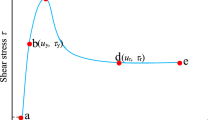
An analytical method has also been proposed by Culmann (1875) to determine the factor of safety, in which the failure surface is created on a sliding plane along the slope. In other words, the slip surface is linear and not circular for simplicity in two-dimensional mode. Table 6 summarizes the results of the Culmann’s method for the conditions that are presented in $\emptyset = 14^\circ ,\,C = 15\,{\text{kN/m}}^{2} , \,\gamma = 15\,{\text{kN/m}}^{3} ,\,H = 8\,{\text{m}}$.

Table 6 Comparison of Culmann’s method with other methods for calculating the safety factor of stability

It can be seen that, with increasing angle of slope, $\beta$, the factor of safety obtained by Culmann’s method is approximated by methods of calculating the factor of safety with method of analysis of finite slope with circular failure surface such as Bishop, Morgenstern–Price, Janbu and Michalowski. Therefore, it can be said that the Culmann’s method provides good results for steep or near-vertical slopes but does not yield satisfactory results for mild slopes (Table 6). Figure 10 provides comparison of six methods for the determination of F_s. Culmann’s plane method differs significantly from the five other methods, especially for larger slope angles. By reducing the slope angle, Culmann’s method for F_s becomes near to the five other methods.

Fig. 10

Comparison of six methods for F_s for condition of $\emptyset = 14^\circ ,\,C = 15\,{\text{kN/m}}^{2} ,\,\gamma = 15\,{\text{kN/m}}^{3} ,\,H = 8\,{\text{m}}$

Slope with steady-state saturated condition

In this section, the slip behavior of the saturated soil along with the water on the slope is investigated. Figure 11a, b provides F_s for the ratio of the h/H (h is water level drawdown, and H is slope height) equal to 0.0 and 0.6875, respectively, for condition $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\, \gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 30^\circ , \,h /H = 0$.

Fig. 11

a Slip circle type changes without water surface drawdown $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} , \gamma = 15\,{\text{kN/m}}^{3} ,\beta = 30^\circ , \frac{h}{H} = 0.$ b Slip circle type changes with water surface drawdown $\emptyset = 14^\circ ,\,C = 25\,{\text{kN/m}}^{2} ,\, \gamma = 15\,{\text{kN/m}}^{3} ,\,\beta = 30^\circ ,\,\frac{h}{H} = 0.6875$

As shown in Fig. 11a, b, there is a change in the water level, the slope is fully flooded and full immersion is achieved with a downward 5.5-m water level. Factor of safety due to the removal of load due to the weight of water on the slope, which is in the direction of stability before the drop of the water level, was reduced by 41.42%. In addition, the slip surface has changed from touch-midpoint circle to slope circle.

Figure 12 illustrates another computational diagram to examine the stability and determining the factor of safety of the slopes exposed to water level drop. In this graph, vertical axis shows the ratio of drop (h/H), in which (h) is the amount of water surface level drop (height of drawdown) and (H) is the height of the slope. It can be observed that by reducing the water surface level on the slope, due to removal of water weight on the slope, factor of safety has become less (assuming pore water pressure does not dissipate). Figure 13 provides the changes in F_s against h/H for stability number (m) for condition of $\beta = 30^\circ , \,\emptyset = 14^\circ$. It can be seen from the figure that when the value of (h/H) approaches the toe of slope (h/H = 1), the factor of safety decreases by decreasing the stability number. Therefore, it can be said that the factor of safety decreases during drawdown of the water level (pore water pressure does not dissipate), but with increase in stability number it will be in a more stable condition.

Fig. 12

Changes in factor of safety (F_s) against relative water level loss (h/H) for the state ($m = 0.125,\;\beta = 30^\circ$)

Fig. 13

Changes in factor of safety (F_s) against relative water level loss (h/H) for the state ($\emptyset = 14^\circ ,\beta = 30^\circ$)

Conclusion

The main purpose of the present study is to investigate the effective different parameters on factor of safety in slopes including soil specific weight ($\gamma$), soil cohesion (C), soil angle of internal friction ($\emptyset$) and geometric parameters of slope including angle with the horizontal ($\beta$), slope height (H) and water level. For this purpose, 192 models were numerically simulated and results were presented as dimensionless graphs and correlation results; the following conclusions can be drawn.

The type of failure circle was investigated and determined that for state (30° < β < 45°), the three types of failure circles (toe, slope or midpoint circle) may occur. For state (45° < β < 60°), two modes of failure may occur: midpoint circle and toe circle. For state ($\beta > 60^\circ$), the mode of failure circle is only toe circle. By dropping the water level by removing the water weight force on the upstream slope, factor of safety of slip was reduced because it reduces the total stress and then reduces the shear strength of soil. Analysis of finite slope with plane failure surface (Culmann’s method) was compared with method of analysis of finite slope with circular failure surface such as Bishop, Morgenstern–Price, Janbu, Michalowski and was observed circular failure methods and logarithmic spiral failure (Michalowski’s method) results relatively the same offer. However, Culmann’s method offers good results for steep slopes and near the vertical but does not yield acceptable results for mild slopes. In the Bishop method, coefficient of determination ($R^{2}$) was lower and value of RMSE (root mean square error) was more than the other methods, but the error of the Bishop’ method is obtained in most cases by 1.34% compared to other methods. It seems that this error can be neglected in comparison with more precise and complex methods. Providing regression equation instead of Michalowski’s charts in the state of dry soil condition to determine factor of safety, F_s, will remove the interpolation method.

The use of numerical models requires time and expertise; in the present study, several regression equations presented using different methods were proposed by researchers which can be used to estimate factor of safety (F_s) without the application of limit equilibrium or simulation methods. The developed regression models in this study do not present any information about the location of the failure surface in this method. On the other hand, use of this method may be useful when we want to study the effects of uncertainties in a reliability analysis. Regression models are simple and often provide an adequate and interpretable description of how the inputs affect the output. Although there are plenty of general purpose advanced geotechnical software such as Plaxis, Limit State, Optum, Midas and, which can deal with any complex problems geometry and soil parameters wise, including pore water pressures, structural elements with interfaces, non-trivial soil models, the developed regression models in addition to design charts can be used for the quick estimation of F_s.