Introduction

There are various problems concerning water movement through porous media. The fluid flow in a porous medium has been considered in various engineering areas, including irrigation engineering, oil engineering, and civil engineering (particularly in water and soil trends). Moreover, this phenomenon is one of the discussed problems in hydraulic structures, especially embankments and earth dams (Milton 2012).

The stability and deformation of hydraulic structures, such as dams, are significantly influenced by the seepage flow within them. Seepage detection through dams and foundations is a key parameter in the design and construction of dams (Chen et al. 2008). The seepage problem can have destructive effects on the dam structure, such as normal elevation of water level, reduction in dam reservoir, dam body instability, soil erosion, and piping. Therefore, seepage analysis is very important in the design of dams and embankments.

Estimation and analysis of seepage flow characteristics are major problems for researchers and engineers. Since it is not possible to analytically solve the governing equations of water seepage, except under very simple and special boundary conditions, researchers have applied empirical, graphical, and recently numerical approaches (Tang et al. 2017). Numerical analysis is the main practical tool for accurately examining the problem. The Boundary Element Method (BEM) (Krikland et al. 1992; Li et al. 1997) is one of the popular approaches, which can simply create geometric changes by relocating the boundary elements. The Finite Volume Method (FVM) (Darbandi et al. 2007) and the Finite Difference Method (FDM) (Jie et al. 2004; Fadaei-Kermani and Barani 2013) have also been used for seepage problems.

Considering its benefits for correcting irregular geometries, the Finite Element Method (FEM) is considered a common tool for analyzing seepage problems (Tien-Kuen 1996; Tayfur et al. 2005). Rahmani-Firoozjaee and Afshar (2007) presented a mesh-free method, known as discrete least square method (DLSM), in order to solve the free surface seepage problem. In addition, Shahrbanozadeh et al. (2015) simulated seepage flow through dams using an isogeometric method. The results agreed well with the experimental measurements.

The application of traditional element-based methods has been investigated in variety of previous studies on seepage problem. The limitations in mesh generation and computation time, as well as difficulties in modeling complex geometries, are often evident in such methods. In recent decades, use of mesh-free methods has become more common for solving partial differential equations (PDEs) due to their several advantages. In this study, smoothed particle hydrodynamics (SPH) method was employed to solve the seepage problem in porous media. The proposed method is a proper meshless approach with a sympatric stiffness matrix, which does not require any background mesh. It is a remarkably versatile and simple mesh-free approach in numerical modeling of fluid mechanics problems, and that there is no need for generating or adapting any mesh. This method can easily deal with large space regions and complicated geometric settings that are completely devoid of particles (Khayyer et al. 2018). Finally, to confirm the results of the proposed method, the finite element code was applied under the same conditions in Geostudio software.

Numerical model

SPH is a meshless Lagrangian method, which yields approximate numerical solutions for fluid dynamic equations through fluid replacement with a particle set. This method was first described for astrophysical simulations in 1977 (Gingold and Moraghan 1997).

In comparison with some particle methods, this method can eliminate mesh with a full Lagrangian view of the problem through attributing characteristics (e.g., smoothing length, density, internal energy, mass, and velocity) to particles (Rafiee et al. 2012). The theory of integral representation of functions is fundamental to SPH. Kernel approximation represents integral representation of the function in SPH (Liu 2010).

In the smoothing kernel function, the contribution of a typical field variable, f(r), is specified at position, r, in space. According to the literature (Liu 2010; Cherfils et al. 2012), the kernel estimate of f(r) is:

$$ f\left( r \right) = \int {f\left( R \right)\bar{W}\left( {r - R,h} \right){\text{d}}R} $$
(1)

where r and R represent the position vectors at different points and h denotes the smoothing length (indicative of the effective function width). \( \bar{W}\left( {r - R,h} \right) \) represents the function of smoothing kernel in SPH. Generally, the weight function has the following characteristics:

$$ \int {\bar{W}\left( {r - R,h} \right){\text{d}}R = 1\quad \mathop {\lim }\limits_{h \to 0} \bar{W}\left( {r - R,h} \right) = \delta \left( {r - R} \right)} $$
(2)

If rij is the distance between particles i and j, then

$$ \overline{{W_{ij} }} = \bar{W}\left( {x_{i} - x_{j} ,h} \right) = \bar{W}\left( {\left| {x_{i} - x_{j} } \right|,h} \right) $$
(3)
$$ \nabla_{i} \overline{{W_{ij} }} = \frac{{x_{i} - x_{j} }}{{r_{ij} }}\frac{{\partial \overline{{W_{ij} }} }}{{\partial r_{ij} }} = \frac{{x_{ij} }}{{r_{ij} }}\frac{{\partial \overline{{W_{ij} }} }}{{\partial r_{ij} }} $$
(4)

Discretization of Eq. 1 represents a summation over all the nearest particles in the region, controlled by the smoothing length for particle i at a specific point of time:

$$ f_{i} = \mathop \sum \limits_{j = 1}^{n} \left( {\frac{{m_{j} }}{{\rho_{j} }}} \right)f_{j} \overline{{W_{ij} }} $$
(5)

where mj and ρj indicate the mass and density of particle j. The spatial derivatives can be approximated as follows:

$$ \nabla f_{i} = \mathop \sum \limits_{j = 1}^{n} \left( {\frac{{m_{j} }}{{\rho_{j} }}} \right)f_{j} \nabla \overline{{W_{ij} }} $$
(6)

Using Eqs. 1–6, the numerical value of function f, as well as its spatial derivatives, can be determined by SPH kernel and particle approximation over a set of smoothing particles.

Numerical model implementation

The two-dimensional governing equation for the flow of seepage through porous media, obeying the Darcy’s law in the steady state, can be formulated as:

$$ \begin{aligned} & \frac{{\partial \left( { - k_{x} \cdot \frac{\partial h}{\partial x}} \right)}}{\partial x} + \frac{{\partial \left( { - k_{z} \cdot \frac{\partial h}{\partial z}} \right)}}{\partial z} = 0 \\ & \left[ {\left( {\frac{{\partial k_{x} }}{\partial x} \cdot \frac{\partial h}{\partial x}} \right) + k_{x} \cdot \frac{{\partial^{2} h}}{{\partial x^{2} }}} \right] + \left[ {\left( {\frac{{\partial k_{z} }}{\partial z} \cdot \frac{\partial h}{\partial z}} \right) + k_{z} \cdot \frac{{\partial^{2} h}}{{\partial z^{2} }}} \right] = 0 \\ \end{aligned} $$
(7)

where kx and kz refer to hydraulic conductivities in, respectively, horizontal and vertical directions and h is the water head. Considering hydraulic conductivity for homogeneous soil, Eq. 7 can be simplified to the Laplace equation:

$$ \begin{aligned} & \frac{{\partial^{2} (kh)}}{{\partial x^{2} }} + \frac{{\partial^{2} (kh)}}{{\partial z^{2} }} = 0 \\ & \frac{{\partial^{2} \varphi }}{{\partial x^{2} }} + \frac{{\partial^{2} \varphi }}{{\partial z^{2} }} = 0 \\ & \nabla^{2} \phi = 0 \\ \end{aligned} $$
(8)

Using SPH method, Eq. 7 can be discretized as:

$$ \begin{aligned} \frac{{\partial k_{x} }}{\partial x} & = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {(k_{x} )_{j} - (k_{x} )_{i} } \right)\frac{{x_{j} - x_{i} }}{{\left| {r_{ij} } \right| + \eta }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} }}{{\partial r_{ij} }}} \\ \frac{{\partial k_{z} }}{\partial x} & = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {(k_{z} )_{j} - (k_{z} )_{i} } \right)\frac{{z_{j} - z_{i} }}{{\left| {r_{ij} } \right| + \eta }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} }}{{\partial r_{ij} }}} \\ \end{aligned} $$
(9)
$$ \begin{aligned} \frac{\partial h}{\partial x} & = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {(h)_{j} - (h)_{i} } \right)\frac{{x_{j} - x_{i} }}{{\left| {r_{ij} } \right| + \eta }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} }}{{\partial r_{ij} }}} \\ \frac{\partial h}{\partial z} & = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {(h)_{j} - (h)_{i} } \right)\frac{{z_{j} - z_{i} }}{{\left| {r_{ij} } \right| + \eta }}\frac{{\partial \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} }}{{\partial r_{ij} }}} \\ \end{aligned} $$
(10)
$$ \begin{aligned} \frac{{\partial^{2} h}}{{\partial x^{2} }} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {\frac{{4\Delta x^{2} }}{{\left| {r_{ij} } \right|^{2} }} - 1} \right)\left( {\frac{{(h)_{j} - (h)_{i} }}{{\left| {r_{ij} } \right|^{2} + \eta }}} \right)\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} \cdot r_{ij} } \hfill \\ \frac{{\partial^{2} h}}{{\partial z^{2} }} = \sum\limits_{j} {\frac{{m_{j} }}{{\rho_{j} }}\left( {\frac{{4\Delta z^{2} }}{{\left| {r_{ij} } \right|^{2} }} - 1} \right)\left( {\frac{{(h)_{j} - (h)_{i} }}{{\left| {r_{ij} } \right|^{2} + \eta }}} \right)\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} \cdot r_{ij} } \hfill \\ \end{aligned} $$
(11)

For homogeneous soil where kx = kz, the SPH discretized form of Eq. 8 can be written as:

$$ \nabla^{2} \phi = \sum\limits_{j} {\frac{{ 2 {\text{m}}_{j} }}{{\rho_{j} }}} \left( {\frac{{\phi_{i} - \phi_{j} }}{{|r_{ij} |^{2} + \eta^{2} }}} \right)\nabla_{i} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W}_{ij} \cdot \vec{r}_{ij} = 0 $$
(12)

where \( \eta = 0.1h \), and it is applied to avoid dividing by zero during calculations.

Solution algorithm

At first, the solution domain, number of particles, initial distance between particles, and also particles’ position are determined. Then, according to particles’ density which equals water density, the mass of all particles is calculated using Eq. 13:

$$ m_{i} = m_{j} = \frac{{\rho_{i} = \rho_{w} }}{{\sum\limits_{j} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W} \left( {\left| {r_{i} - r_{j} } \right|,h} \right)} }} $$
(13)

The initial particles’ water head at boundary layers is specified with respect to the initial conditions at upstream and downstream. The particles’ density is calculated using Eq. 14:

$$ \rho_{i} = \sum\limits_{j} {m_{j} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{W} } \left( {\left| {r_{i} - r_{j} } \right|,h} \right) \, $$
(14)

where mi and ρi are the mass and density of particle i, mj and ρj are the mass and density of neighbor particles, and h is the smoothing length. Finally, by solving governing equations, the values of water head for each particle and other parameters including seepage velocity and discharge can be calculated, respectively. Figure 1 represents the SPH model algorithm for seepage problem in porous media.

Fig. 1
figure 1

SPH model algorithm for seepage problem in porous media

Full size image

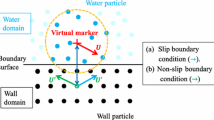
Boundary conditions are required at the solution domain boundaries. The boundary conditions governing the Laplace equation solution in seepage analysis can be specified as:

Dirichlet boundary condition is set to boundaries with constant water head for free surface of water at upstream and downstream. For the particles with Dirichlet boundary condition, the Laplace equation is not solved. Neumann boundary condition is set to impermeable boundaries or boundaries with specified function derivative values.

Results and discussion

To evaluate the effectiveness and practicability of the proposed model, two different seepage problem cases are implemented: seepage through concrete dam foundation and seepage through earth dam. To verify the SPH method results in seepage flow simulation, the finite element-based software, namely Geostudio (SEEP/W), has been implemented under the same conditions.

Geostudio (SEEP/W) software is a powerful finite element-based geotechnical program, capable of solving two-dimensional seepage problems with multiple soil layers (GEO-SLOPE 2012).

Seepage through concrete dam foundation

Seepage analysis of dam foundation is very important in stability analysis of this structure. Moreover, uplift force can be calculated by analyzing seepage through dam foundation. In case-1, seepage through a concrete dam foundation is investigated. The features of the model are presented in Table 1.

Table 1 Features of the foundation seepage model
Full size table

Utilizing the SPH method, seepage through the dam foundation was simulated. The initial distance between particles was considered 0.5 m. The smoothing length was selected 0.6 (h = 1.2r). Moreover, SEEP/W model is employed to verify the analytical results obtained by SPH. Figure 2 shows geometry and geotechnical section of the dam foundation introduced to SEEP/W software.

Fig. 2
figure 2

Geometry and geotechnical section of the dam foundation introduced to SEEP/W

Full size image

Figure 3 shows the numerical results of water head values based on the SPH modeling and SEEP/W software results. It can be seen that the results agreed well, and the process of water movement through dam foundation has been modeled properly. Moreover, the boundary conditions have been applied well in modeling in which the equipotential lines are perpendicular to impermeable layers and dam base. The seepage discharge calculated by SEEP/W software and SPH method is 1.3106 × 10−8 m3/s and 1.2254 × 10−8 m3/s, respectively. The difference is about 6.5% that shows a reasonable agreement between results.

Fig. 3
figure 3

Equipotential lines of seepage water in SEEP/W and SPH method

Full size image

Seepage through earth dam

As seepage analysis is necessary for earth dams, determining seepage force and piping potential is required for stability analysis of these structures. In case-2, seepage through an earth dam is investigated, and the features of the relevant model are presented in Table 2.

Table 2 Features of the earth dam seepage model
Full size table

Seepage through the earth dam and its foundation has been modeled using SPH method and SEEP/W software. Figure 4 shows geometry of the earth dam introduced to SEEP/W software. The numerical results of water head values based on the SPH modeling and SEEP/W software results are represented in Fig. 5. As it is exposed, the water equipotential lines clearly demonstrate the excellent agreement of the present model results to those of SEEP/W software. The flow lines have been modeled accurately on free surface that show the well implementation of boundary conditions. Moreover, the calculated seepage discharge through the earth dam and foundation from the SEEP/W software is 4.9789 × 10−6 m3/s. The seepage discharge obtained by the present method is 5.6074 × 10−6 m3/s. Figure 6 shows the seepage velocity vectors through earth dam. There is a good agreement between SPH and SEEP/W model results.

Fig. 4
figure 4

Geometry and geotechnical section of the earth dam introduced to SEEP/W

Full size image
Fig. 5
figure 5

Equipotential lines of seepage water in SEEP/W and SPH method

Full size image
Fig. 6
figure 6

Seepage velocity vectors through earth dam

Full size image

Conclusions

In this paper, the applicability of a mesh-free method, namely smoothed particle hydrodynamics (SPH) method, for analyzing seepage problem in porous media has been investigated. Two different seepage problem cases were considered: seepage through concrete dam foundation and seepage through earth dam. In order to verify the proposed method results in seepage analysis, a well-established seepage software has been employed in parallel. The agreement between SPH method results with those from SEEP/W model proves that the SPH technique is capable of seepage problem analysis. In this method, there is no need to mesh computation domain compared with traditional mesh-based methods. Moreover, using a set of nodes scattered over the computation domain, the SPH method can properly model seepage problem because of its good performance, especially in complex boundaries.