Introduction

The presence of toxic heavy metals in the industrial effluents raises concern over their acute toxicity to human health (Mohapatra and Anand 2007; Leyva-Ramos et al. 1997).Among the hazardous toxic metals, cadmium (Cd2+) is one of the most toxic heavy elements to which man can be exposed. Accumulating in human kidney cortex causes malfunction of kidney (Sethi et al. 2006; Nordberg 2009; Järup et al. 1998). The maximum limit suggested by the WHO is summarized in Table 1.

Table 1 Maximum limits of heavy metals suggested by the World health organization (WHO)
Full size table

Cadmium is mainly used in the rechargeable batteries, production of special alloys, solar cells and coating (electroplating) (Katırcıoğlu et al. 2008).New revealing approaches such as membrane filtration, hybrid methods (floatation–filtration) are very costly and not feasible when metals are in huge volumes at relatively low concentrations, i.e. less than 100 ppm (Patterson 1985; Rao and Gupta 1982; Blöcher et al. 2003). In recent times, while important advances in knowledge have come out, biosorption proved to be an effective technology in industrial and environmental remediation of toxic heavy metals (Eccles 1999). Among the diverse types of biosorbents (i.e. fungi, bacteria, algae, lignocellulosic materials, industrial waste), algal biomass has proven to be a highly effective and economical technology for its ability to remediate/adsorb toxic metals (Ramelow et al. 1992; Holan and Volesky 1994).

In the present study, isolated green algae Chlorella vulgaris was used as biosorbents with an objective of removing Cd (II) from industrial effluents. It examines the importance of green algae Chlorella vulgaris as a potential biosorbent which was characterized by morphological parameters by employing scanning electron microscope (SEM) equipped with energy-dispersive spectroscopy (EDX) and various functional groups involved in adsorption by FTIR analysis. It also includes isolation of green algae Chlorella vulgaris, the effect of various fundamental parameters over sorption process, adsorption isotherms and kinetics that are at play in the biosorption of Cd (II) by green algae Chlorella vulgaris. This study is also devoted to outlining the importance of desorption of Cd (II) with many affecting parameters and recovery of metal ions.

Materials and methods

Microalgae strain and mass culture

The algal samples were collected from the water pond in Harcourt Butler Technological university campus, Kanpur. The samples were inoculated in the autoclaved Fog’s medium in 100-mL test tubes at room temperature in open laboratory in natural sunshine (17:7 h photoperiod) for forty days (Becker 1994). Culture was streaked in agar plates of same medium and by using standard manual for algae, and Chlorella vulgaris was confirmed. The isolated algae Chlorella vulgaris were inoculated in 200 mL fog’s medium in a 250-ml flask, were put in a shaker for one week in room temperature (35 ± 2 °c) in white florescent light of moderate intensity and stepwise transferred to 500 mL and then to one litre flasks up to 90% of its capacity. Growth was monitored by measuring OD at a wavelength of 686 nm (Piotrowska-Niczyporuk et al. 2012).

Dry weight of algae was calculated by using the relation:

$${\text{Biomass}}\;\left( {{\text{dry}}\;{\text{weight}}} \right) \, \left( x \right) \, = \, 0.2936*{\text{O}} . {\text{D}} .\;686\;{\text{nm}} + 0.0007$$
(1)

Preparation of metal ion solution

A stock solution of Cd (II) was prepared by dissolving 2.744 gm of cadmium nitrate Cd(NO3).4H2O in 1000 ml of deionized water. All the chemicals used in the experiment were procured from Merck and of analytical grade. Prepared working solutions of different concentrations from stock solution with adequate dilution Standard solutions of Cd (II) were obtained from BIS (Bureau of Indian Standards), Delhi, India.

Preparation of adsorbent

The biosorbent used in this work was harvested by filtering the culture medium through cellulose nitrate membrane filter of pore size 45 Âµm. The filtered biomass was washed several times with distilled water and dried in an oven at 60 °C for 1 day (Yadav et al. 2014). They were made of size 250–300 µm by sieving and stored in a desiccator.

Characterization of the adsorbent

The elemental composition of biosorbents was analyzed by using elemental analyzer (Eurovector EA 3000, Germany), and functional groups present on the surface of algal biosorbents were analyzed by Fourier transform infrared (FTIR) spectroscopy (Bruker FTIR Vertex 70, Germany) in the specified range. Scanning electron microscope (SEM, Zeiss, Sigma VP, with EDAX) was used to see the surface morphology of biosorbent. Double-beam UV–VIS spectrophotometer (UV Pharmspec 1700, Shimadzu) was used for algal growth estimation, and Atomic absorption spectrophotometer (AA240, Agilent) was used for estimation of adsorbed heavy metal.

Adsorption experiment

Kinetic experiment was performed in continuously stirred flasks (250 mL) containing 100 ml of stock solutions of different concentrations and 1 g of biosorbent. Sample of 2 ml solution was withdrawn in specific regular intervals and analyzed by AAS at 480 nm for residual Cd solution (Yadav et al. 2013). Initial batch sorption experiments were carried out for optimization of pH (1–6), adsorbent concentration (0.2 to 3 g 100 mL−1) and metal concentration (10–120 mg L−1). Experiments were carried out at room temperature 35 °C, and pH of solution was adjusted by 0.1 N HCl or 0.1 N NaOH. The percentages of Cd removal ‘R’ and qe (mg/g), that is amount of metals adsorbed per unit of the mass of the adsorbent, were determined using formulas (2) and (3) (Chen et al. 2005).

$${\text{Removal}}\;{\text{of}}\;{\text{Cd}}\;\left( {\text{II}} \right) \, \left( \% \right) \, R = \, \left( {C_{\text{i}} - C_{\text{e}} /C_{\text{i}} } \right) \, 100$$
(2)
$${\text{Cd}}\;\left( {\text{II}} \right)\;{\text{uptake }}\left( {q_{\text{e}} } \right) \, = \, \left( {C_{\text{i}} - C_{\text{e}} /M} \right) \, V$$
(3)

where Ci and Ce (mg/L) are initial and equilibrium concentrations, V is volume of solution (L) and M is the weight of adsorbents (g).

Desorption experiments

For the desorption study, algal biomass (0.1 g) was incorporated with 50 ml Cd (II) solution (100 ppm).The loaded algal biomass was filtered and washed 2 to 3 times from distilled water. Further, it was treated with 50 ml desorbent solutions (0.1 N)of each HNO3, EDTA, HCl, H2SO4 separately. This mixture was kept for 2–3 h in shaker, and further collected supernatant was analyzed for Cd (II)(Hashim and Chu 2004). Desorption ratio was calculated from the amount of metal ions adsorbed on the biomass and the final metal ion concentration in desorption medium, as the following equation:

$${\text{Desorption}}\;{\text{ratio}} = \,({\text{Amount}}\;{\text{of}}\;{\text{metal}}\;{\text{ions}}\;{\text{desorbed}}/{\text{Amount}}\;{\text{of}}\;{\text{metal}}\;{\text{ions}}\;{\text{adsorbed}}) \times 100$$
(4)

Effect of time, temperature on desorption capacity, concentration vs desorption capacity on algal biomass were also evaluated.

Kinetic study

The most important factor in adsorption is predicting at what rate adsorption takes place in adsorption system design. Mechanism of biosorption and rate-controlling step are also essential outcomes in the kinetic study. When the initial concentration of solute is low, the adsorption process obeys the pseudo-second-order model. Conversely, pseudo-first-order models can be applied to higher initial concentrations (Azizian 2004).

Pseudo-first-order model

$${ \log }\;\left( {q_{\text{e}} - \, q_{\text{t}} } \right) = { \log }\;q_{\text{e}} - \left( {k_{1} /2.303} \right)t$$
(4)

where qt and qe are the amounts of metal ions adsorbed (mg/g) at time t and at equilibrium, respectively, and k1 is the rate constant of pseudo-first-order adsorption (min−1)(Lagergren 1898).

Pseudo-second-order model

It is represented by the equation:

$$t/q_{t} = 1/(k_{2} q_{\text{e}}^{2} + \, \left( {1/q_{\text{e}} } \right)t$$
(5)

here qe and qt are the adsorption capacities at equilibrium and time t (mg/g), respectively, k2 is the rate constant of the pseudo-second-order sorption (g/mg min). The plots of t/qt versus t gave linear plot (Ho and McKay 1999). The values of the adsorption parameters qe and k2 were determined from the slope and intercept of the plot, respectively.

Intraparticle diffusion model

To know the mechanism and rate-controlling steps in the kinetic of biosorption, intraparticle diffusion model provides adequate information. The intraparticle diffusion model is (Weber and Carrell Morris 1963) given by Eq. (6):

$$q_{t} = \, k_{\text{i}} t^{0.5} + \, I$$
(6)

where ki is the intraparticle diffusion rate constant and I is the intercept of the intraparticle diffusion plot. The value of ki was calculated from the slope of plot qt vs t0.5.

Thermodynamic studies

The thermodynamic parameters such as ΔH0, ΔS0 and ΔG0 were calculated from the adsorption data. Kc, the equilibrium constant was determined by Eq. (7) (Aksu 2002).

$${\text{Kc}} = C_{\text{A}} /C_{\text{e}}$$
(7)

where CA (mg/L) is the concentration of solute in the aqueous phase and Ce is the equilibrium concentration (g/L). Then, ΔG0 by expression:

$$\Delta G^{0} = - \,RT\;\ln \;{\text{Kc}}$$
(8)

The value of ΔS and ΔH was determined by

$$\log \;{\text{Kc}} = \Delta S/2.303 - \Delta H/2.303\;{\text{RT}}$$
(9)

Adsorption isotherms

Various adsorption isotherm models have been investigated to find adsorption efficiency for metal ions from the solution. The maximum uptake of Cd (II) by algal adsorbent was determined by fitting the adsorption data to Langmuir and Freundlich. To investigate the prevalence of physical or chemical process in adsorbing heavy metal ions from aqueous solution, Dubinin–Radushkevich isotherm model was also studied.

Langmuir isotherm model

The Langmuir isotherm describes uniform adsorption with no cross-migration of adsorbate on a surface having finite number of adsorption sites that are monolayer adsorption (Langmuir 1916). To ensure equilibrium conditions, the linear form of the Langmuir isotherm model (Eq. 10) was applied to the experimental data as

$$C_{\text{e}} /q_{\text{e}} = \left( {1/bq_{\text{m}} } \right) + \left( {C_{\text{e}} /q_{\text{m}} } \right)$$
(10)

where Ce, qm, and b are the concentration of adsorbate at equilibrium (mg/L), maximum adsorption capacity (mg/g), and Langmuir constant (L/mg), respectively. Equation (10) expresses a dimensionless constant separation factor or equilibrium parameter (RL) in Langmuir isotherm

$$R_{\text{L}} = \left( {1/1 + bC_{\text{i}} } \right)$$
(11)

where the initial solute concentration is donated by Ci and b is the Langmuir’s adsorption constant (L/mg). The RL value confirms the adsorption to be unfavourable (RL > 1), linear (RL = 1), favourable (0 < RL < 1), or irreversible (RL = 0).

Freundlich isotherm model

The Freundlich isotherm is used as an empirical model for the adsorption process of heavy metal ions (Ho et al. 2005). Equation (12) describes the empirical Freundlich isotherm as:

$$\ln \;q_{\text{e}} = \ln K_{\text{F}} + 1/n\;\ln C_{\text{e}}$$
(12)

where qe is amount of metal ion adsorbed on to surface of algal biomass at equilibrium (mg/g) and Ce is the equilibrium concentration of the adsorbate (mg/L). KF is the adsorption constant that corresponds to adsorption capacity whereas 1/n to the adsorption intensity. n depends on the adsorbate and adsorbent. Any value of n, higher than unity, favours the adsorption process.

Results and discussion

Characterization of algal bioadsorbent

Algal growth

The algal growth and increase in biomass were calculated by spectrophotometric method (McGinn et al. 2012). The biomass content obtained after 30 days (0.332 g/L) was the greatest. The algal strain continued to show an increase in growth for 30 days after which the growth attained saturation as the cells entered in saturation phase. After 40 days, the cells started entering the decline phase showing a decrease in the biomass. Figure 1 shows growth curve of C. vulgaris.

Fig. 1
figure 1

Growth curve of C. vulgaris: temperature (35 ± 2 °c), OD at 686 nm, time (till 40 days)

Full size image

Elemental analysis

To explain the mechanism and behaviour of sorption process, physiochemical parameters provide essential insights into the biosorption of metallic ions. The percentage of major elements C,H,O,N,S in powdered form of algae Chlorella vulgaris were presented in Table 2.

Table 2 Characteristics of parameters of algal biomass
Full size table

The pore size of algal biosorbents was 3–9 micrometre, and the radii of cadmium ion was 95 pm (Pauling 1960).The smaller ionic radii of cadmium ion and larger pore size of algal biosorbent facilitate higher adsorption. Surface area of biosorbent plays an important role in the adsorption process. The average surface area of biosorbent was estimated about 12 m2/g which is very much favourable for the sorption of heavy metals.

FTIR analysis

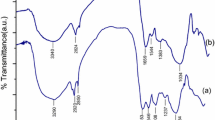
FTIR analysis (Fig. 2) depicts the various peaks arisen due to various functional groups present on the surface of biosorbent. The broad peak around 3485 cm −1 belongs to –NH and –OH groups, stretching frequency around 2945 cm −1 attributed to –CH, peak at 1674 shows the vibrational frequency of carbonyl (C=O) group, 1267 cm −1 assigned to –CH3 group(Sharma and Bhattacharyya 2005). The other lower peaks ascribed to C-N and –C=S groups (Tunali et al. 2006). After absorbing the Cd (II) ions, the various vibrational frequencies reduced which confirms the bonds formation by Cd (II) to carboxyl, carbonyl, hydroxy, amine and amido groups.

Fig. 2
figure 2

FTIR spectra of virgin chlorella and loaded with Cd (II) metal ions

Full size image

SEM analysis

The SEM-analyzed image of virgin algal biomass revealed the asymmetric porous, heterogeneous surface having cavities which facilitate the biosorption of the cadmium (II) ions on the surface of algal biomass Fig. 3a. After getting the metal adsorbed, the surface of algal biomass became smoother and compact Fig. 3b.

Fig. 3
figure 3

Scanning electron microscopic images of a virgin biomass of Chlorella vulgaris, b Cd (II) loaded biomass of Chlorella vulgaris

Full size image

Effect of solution pH

The hydrogen ion concentration is an important parameter affecting the adsorption. The degree of ionization of adsorbate and surface charge of adsorbent are very much influenced by the pH. The batch sorption studies have been carried out within the pH range of 1–6. The obtained results are shown in Fig. 4. Percentage removal of metal ions is comparatively very less at lower pH which revealed that higher hydrogen ion concentrations compete to metal ions for site on adsorbent and it gets protonated which left very less site for the adsorption of metal ions(Lalhruaitluanga et al. 2010; Ibrahim and Sani 2014). About 90% of the removal takes place at pH 4.5 which is the maximum in the present study. As pH increases deprotonation takes place and sites get available to the metal ions and that is the reason the percentage of removal increases (Ibrahim et al. 2006).

Fig. 4
figure 4

Effect of pH on adsorption of Cd (II) on to Chlorella vulgaris biomass: Ci = 100 mg/L, dose = 1 g/L, contact time = 2 h and room temperature

Full size image

Effect of initial metal concentration, contact time and biomass dosages

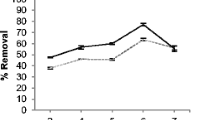
The effect of initial metal concentrations was studied under batch conditions: pH = 4.5, dose = 1 g/L, contact time 2 h at room temperature of concentration range 10–100 ppm. As we increase the metal ion concentrations of cadmium (20 to 100 ppm), the biosorption capacity increases (16–62.3 mg/g), respectively. Figure 5a shows the fact that the increase in metal ion concentration decreases the mass transfer resistance between metal ions and biosorbents and that facilitated to reach the sites that’s why adsorption capacity increases and after further increase in concentration have no effect on adsorption capacity due to the saturation of binding sites. At the same time, percentage removal decreases from 97.2 to 40.9 because at the lower initial concentration, a higher number of sites are available per mole of metal ions but as number of moles of metal ion increases(Nasir et al. 2007), sites were occupied by ions that lead to a decrease in the removal percentage shown in Fig. 5b.

Fig. 5
figure 5

a Effect of initial metal concentration on adsorption of Cd (II) on to Chlorella vulgaris biomass: pH = 4.5, dose = 1 g/L, contact time = 2 h, room temperature. b Effect of initial metal concentration on adsorption of Cd (II) on to Chlorella vulgaris biomass: pH = 4.5, dose = 1 g/L, contact time = 2 h, room temperature. c Effect of contact time on concentration on adsorption of Cd (II) on to Chlorella vulgaris biomass: pH = 4.5, initial concentration of Cd (II) = 100 mg/L, dose = 1 g/L, room temperature. d Effect of biomass dosage on adsorption of Cd (II) on to Chlorella vulgaris biomass: pH = 4.5, Ci = 100 mg/L, contact time = 2 h and room temperature

Full size image

In the case of contact time, adsorption rate increases with time and after getting maximum (saturation) it tends to adsorb metal with a constant rate as we can depict in Fig. 5c. It has been observed that initially till 50 min, adsorption capacity increases significantly, and thereafter it proceeds at a slower rate comparatively and finally beyond 55 min, no significant metal uptake rate observed.

To examine the effect of biosorbent dose (0.5–2 g/L), batch sorption studies at fixed initial concentration of 100 mg/L, contact time of 2 h and at room temperature was done. Here we observed increased metal biosorption by increasing biomass dosages because of increased active sites and available surface area (Shen et al. 2008). Here, we can see in Fig. 5d, after reaching the saturation or equilibrium (adsorbent dose approximately 2 g/L), metal uptake had become unchanged afterwards due to concentration gradient between the sorbent and sorbate.

Adsorption kinetics

Mechanism involved in biosorption was analyzed by three kinetic models: the pseudo-first-order kinetics, pseudo-second-order kinetics and intraparticle diffusion models by fitting experimental values. The kinetic parameters obtained at initial concentration 100 ppm are summarized in Table 3.

Table 3 Pseudo-first-order, pseudo-second-order and intraparticle diffusion rate for adsorption of Cd (II) on algal biomass
Full size table

Pseudo-first-order, pseudo-second-order kinetic model and intraparticle diffusion model

The calculated qe(24.9 mg/g) value obtained from pseudo-first-order model did not fit properly with the experimental value (62.3 mg/g), and at same time the correlation coefficient value is not up to mark as shown in Fig. 6a which made it clear that this model does not describe the adsorption process (Oliveira et al. 2008).

Fig. 6
figure 6

a Pseudo-first-order plot for adsorption of Cd (II) on algal biomass: pH = 4.5, Ci = 100 mg/L. dose = 1 g/L, contact time = 60 min at room temperature. b Pseudo-second order plot for adsorption of Cd (II) on algal biomass: pH = 4.5, Ci = 25, 50, 100 mg/L. dose = 1 g/L, contact time = 60 min at room temperature. c Intraparticle diffusion model for adsorption of Cd (II) on algal biomass: pH = 4.5, Ci = 100 mg/L. dose = 1 g/L, contact time = 60 min at room temperature

Full size image

It could be seen that the calculated (65.9 mg/g) and experimental values (62.3 mg/g) showed nice agreement in pseudo-second-order kinetic model. Figure 6b shows the correlation coefficient is very much close to unity. These results concluded that the pseudo-second order kinetic model best describes the adsorption kinetics of the present study.

The linear plot of qt versus t0.5 showed (Fig. 6c) that biosorption process has intraparticle diffusion which helps in defining the mechanism of adsorption, but intraparticle diffusion is not rate limiting because the line does not pass through the origin (Freundlich 1907; Mane et al. 2007) which revealed there might be some other kinetic models also which help in controlling the rate.

Thermodynamics of adsorption

Thermodynamics of adsorption studies were performed at temperatures 300 and 330 K. Plot of ln Kd versus 1/T gives rise to ∆H and ∆S as slope and intercept, respectively. Results obtained are summarized in Table 4. ∆G (− 0.235, − 0.339) have shown negative values which confirm the feasibility of reactions at given temperatures (300 and 330 K). Positive values of enthalpy ∆H (endothermic adsorption) and randomness (∆S) indicate the feasibility of adsorption process (Li et al. 2008).

Table 4 Thermodynamic parameters
Full size table

Adsorption equilibrium

Langmuir isotherm model

The value of qm and b was calculated from the slope and intercept of plot between ce/qe versus ce (Fig. 7a). Obtained qm in the present study was 97.43 mg/g (Table 5) which makes it a very reliable bioadsorbent. The correlation coefficient (0.9901) indicates the adsorption of cadmium ions on algal biomass followed Langmuir isotherm. The value of RL for the adsorption was 0.014–0.031 which makes it clear that this adsorption process is favourable.

Fig. 7
figure 7

a Langmuir isotherm plot for adsorption of Cd (II) on algal biomass of Chlorella vulgaris: pH = 4.5, Ci = 25–100 mg/L, dose = 1 g/L, time = unit hour at room temperature. b Freundlich isotherm plot for adsorption of Cd (II) on algal biomass of Chlorella vulgaris: pH = 4.5, Ci = 25–100 mg/L, dose = 1 g/L, time = unit hour at room temperature

Full size image
Table 5 Langmuir and Freundlich adsorption isotherm constants and parameters for adsorption of Cd (II) on algal biomass
Full size table

Freundlich isotherm model

KF is an adsorption constant that corresponds to adsorption capacity whereas 1/n to the adsorption intensity. n depends on the adsorbate and adsorbent. Plot of qe versus ln ce gives rise to the value of Kf and n as shown in Fig. 7b. Value of n (1.73) higher than unity favours the adsorption process (Table 5).When we compare the Langmuir and Freundlich adsorption isotherms of algal biomass for heavy metal ion Cd (II)) with the practical values given in Table 5 and Fig. 7a, b, we can easily figure out that both Langmuir isotherm and Freundlich isotherms display a higher regression coefficient (R2) as both models could fit but Langmuir isotherm model was the best fit to this adsorption process.

Desorption studies and recyclability

Cost effectiveness is one of the most important factors for industrial feasibility of bioadsorbent, so it is desirable to regenerate and reuse. Recyclability of algal bioadsorbent was evaluated by (0.1 Mof HNO3, HCl, H2SO4 and EDTA).Results show that HNO3 (0.1 N) is a more effective eluting agent than the rest as shown in Fig. 8a. Since HNO3 can nitrify and damage the adsorbent in high concentration (Deng et al. 2008), it is not preferred as a desorbating agent rather EDTA is preferable because of its high affinity to form complex with Cd (II) without any damage to the algal adsorbent (Kordialik-Bogacka 2011).

Fig. 8
figure 8

a Cd (II) recovery by different desorbents. b Effect of EDTA concentration on desorption capacity of algal biomass (sample dose 0.1 g, temperature 55 °C; time 45 min). c Effect of temperature on desorption capacity of algal biomass. (sample dose 0.1 g, EDTA concentration 0.1 mol/L; time 45 min.) d Effect of time on desorption capacity of algal biomass. (sample dose 0.1 g, EDTA concentration, 0.1 mol/L.)

Full size image

Effect of EDTA concentration, temperature and time on desorption.

Desorption capacity over different EDTA concentrations was evaluated on the algal biosorbent. Results are shown in Fig. 8b. The desorption capacity increases with increase in the concentration of EDTA at the starting and then gets decreased. The reason might be, initially at low concentrations it desorbs Cd (II) by exchanging the ions but as we increase the concentration of EDTA the desorbed Cd (II) also gets accumulated and causes hindrance in desorbing Cd (II) afterwards. The maximum desorption capacity of algal biomass was reached at 87.2 mg/g at an EDTA concentration of 0.1 mol/L.

The effects of different desorption temperatures on Cd (II)-loaded algal biomass desorption capacity are shown in Fig. 8c. The findings show that desorption capacity of algal biomass increases initially with increase in temperature till 55 °C but after this desorption capacity decreases sharply, which shows that the temperature range (50–55 °C) is the best for desorption(Jalali et al. 2002).

The effect of different desorption times on algal biomass was studied with EDTA of 0.1 mol/L shown in Fig. 8d. Result shows that desorption capacity first increased, reached maximum at 55 min and again decreased with time. The cause for this result might be initially EDTA had high capacity (unoccupied sites) to attract metal ions but after getting saturated with coordination bond with metal ions the sites occupied and desorption capacity decreased

To investigate its reproducibility of algal biomass, five cycles of adsorption and desorption were repeated at fixed optimum conditions (temp 55 °C, biomass dose 0.1 g, time 55 min, EDTA concentration 0.1 mol/L). Investigated results showed that removal efficiency was decreased from 84.2 to 79.3 after five cycles which reveal its applicability in industrial purpose.

Conclusions

The results obtained in this study demonstrated that isolated Chlorella vulgaris that is easily available at very low cost could be very effective in the removal of heavy metal Cd (II) not only among algal biomass (Jalali et al. 2002; Lodeiro et al. 2006)but also among other low-cost biomasses comparatively (López-Mesas et al. 2011; Lalhruaitluanga et al. 2010). The sorption capacity of algal biomass at initial concentration 100 ppm, pH 4.5–5 at room temperature was 62.3 which is quite fast and equilibrium reached within one hour. FTIR and SEM studies validated the interaction between various functional groups present on the surface of adsorbent and heavy metals. Biosorption data fit well to Langmuir isotherm model and partially to Freundlich. Experimental results suggest that pseudo-second-order reaction kinetics was followed by biosorption, and it seems other than intraparticle diffusion other kinetic models are also responsible for controlling the rate of reactions. 0.1 N EDTA was a good eluting agent at 55 °C temperature taking about one hour time. Regeneration also seems effective, but further assessment of economic study is needed for industrial upscaling. In this context, the development of commercial biosorbents by immobilization techniques would be very effective.