Introduction

Dyes have been the subject of much interest in recent years (Abou Taleb et al. 2012). Discharging dyes produced during various industrial activities can be harmful to aquatic life and human beings. Dyes can cause allergy, dermatitis, and skin irritation and also provoke cancer and mutation in humans. The presence of dyes in aqueous environments can reduce light penetration and subsequently photosynthesis (Abou Taleb et al. 2012; Hassani et al. 2015). They are also aesthetically unpleasant to drink and for other purposes. Therefore, decolorization of wastewater has become one of the major issues in wastewater pollution (Abou Taleb et al. 2012; Sarwan et al. 2012).

Natural organic matter is ubiquitous in soil or aquatic environments, and humic acids (HA) account for the largest proportion (40–90%) (Zermane et al. 2013). Humic acid is a natural macromolecule that contains many organic functional groups such as carboxylic, phenolic, and hydroxyl (Liu et al. 2015). Moreover, HA is troublesome not only for causing color, odor, and taste problems but also for forming trihalomethanes and other halogenated organic compounds that exhibit mutagenic properties during the chlorination step in drinking water treatment (Zhang et al. 2015).

Several treatment techniques of dye and HA removal have been studied and developed, including physical (adsorption, filtration, ion-exchange, irradiation, etc.), chemical (oxidation, coagulation, etc.), and biological (microbial discoloration) methods (Dalvand et al. 2016; Gomes et al. 2015). Physical methods are found to be easier and more economical. Adsorption processes belong to this category and were found to be effective when applied in the liquid phase (Chiew et al. 2016; Anirudhan and Ramachandran 2015).

Various kinds of competent adsorbents have been reported (Yang et al. 2012). Activated carbon is the most widely used adsorbent to remove contaminants from wastewater because of its extended surface area, microporous structure, high adsorption capacity, and a high degree of surface reactivity (Maghsoodloo et al. 2011). In general, it is expensive and the regeneration of the adsorbent for several steps may cause difficulties because of the loss of the textural properties. Consequently, this problem has led to a search for cheap and efficient alternate material such as sawdust, zeolite, chitosan, bentonite, and clay (Elsherbiny 2013; Shojaat et al. 2016). The application of silica-based clays and polymers is favored for the adsorption of various organic pollutants. Among various siliceous materials, expandable layered silicates as montmorillonite (MMT) have received much more attention due to their low cost, availability, stability, and non-toxicity. However, it is difficult to keep fine MMT particles in the aqueous phase. Therefore, the immobilization of fine particles within a suitable polymeric matrix is considered to overcome this problem (Hassani et al. 2015; Soltani et al. 2013). Alginate biopolymer is isolated from brown algae and can also be synthesized from microorganisms (Alboofetileh et al. 2013; Sui et al. 2012). It is the only polysaccharide that naturally contains carboxyl groups in each constituent residue and has various abilities for application as a functional material. Its range of excellent properties, such as low cost, non-toxicity, biocompatibility, biodegradability, and reproducibility, has led to its use in many areas (Alboofetileh et al. 2013).

In the present study, the first part deals with the sorption of rhodamine 6G and HA onto composite in a single system. The second part concerns the sorption of these pollutants in mixtures. The effect of various parameters such as contact time, pH, and initial dye concentration on the adsorption of pollutants was considered.

Experiment

Materials

Sodium alginate (viscosity of 1% in water: 15–20 cP), calcium chloride (≥ 99%), humic acid (HA), rhodamine 6G (ethyl 2-[3-(ethylamino)-6-ethylimino-2,7-dimethylxanthen-9-yl]benzoate; hydrochloride, C28H31ClN2O3, 479.01 g/mol), and other chemicals including HCl and NaOH were purchased from Sigma-Aldrich. The name, molecular structure, and the wavelength of maximum absorbance of Rh6G and HA selected for this study are shown in Table 1. The bentonite clay was supplied by the Enterprise Nationale des Substances Utiles et des Produits Non Ferreux, Hammam Boughrara, Algeria. The cation-exchange capacity (CEC) and its chemical composition were found to be 90 meq/100 g; 58.4 SiO2, 1.1 MgO, 16.42 Al2O3, 2.88 Fe2O3, 3.01 MgO, 0.46 CaO, 1.40 Na2O, 2.3 K2O, 0.35 wt% TiO2.

Table 1 Characteristics of Rh6G and HA
Full size table

Preparation of bentonite–alginate composite

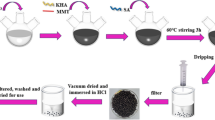
Sodium alginate was dissolved in distilled water 2% (w/v), and then, 2 g of bentonite clay was added. The mixture was stirred and left until it became a homogeneous solution without any bubbles. The mixture was stirred overnight. When the mixture became homogeneous, it was dropped through a burette into an aqueous calcium chloride solution 4% (w/v) with vigorous stirring. The spherical beads formed were kept in CaCl2 solution for 8 h. Then, the beads were filtered, washed with distilled water, and left for drying in a laboratory at 23 °C (Kaygusuz and Erim 2013; Benhouria et al. 2015). The product obtained is named composite.

Structural and textural properties of samples

The textural characteristics of the samples such as specific surface area, external area, and pore volume were determined by conventional N2 adsorption data at − 196 °C using a Quantachrome Autosorb IQ analyzer. Prior to the analyses, the samples were degassed in situ for 12 h at 150 °C to desorb moisture adsorbed on the surface.

The X-ray diffraction analyses were carried out using a Rigaku Miniflex II diffractometer using Cu Kα radiation (λ = 1.5405 Å) and a graphite monochromator, operated at 30 kV and 15 mA. Diffraction pattern was recorded between 5° and 70° (2θ) using increments of 0.02° and accounting time of 2 s.

Fourier transform infrared spectroscopy (FTIR) spectra of bentonite, alginate, and composite were measured in the range of 400–4000 cm−1 with 4 cm−1 of resolution using a Bruker (ALPHA) FTIR spectrometer.

The point of zero charge (pHpzc) was determined according to the method described by Benhouria et al. (2015). Briefly, the initial pH (pHi) of aqueous solutions (100 cm3) was adjusted to a pH range of 2–12 using 0.1 M HCl or NaOH. Then, 0.1 g of adsorbent was added to each sample. The dispersions were stirred for 24 h at 23 °C, and the final pH (pHf) of the solutions was measured. The point of zero charge was obtained from a plot of pHf–pHi versus pHi.

Batch adsorption experiments

Kinetic studies in single systems were conducted in a beaker at 23 °C and pH = 6 by shaking 0.2 g of the sorbent with 200 cm3 of a solution containing Rh6G (20–800 mg/dm3) or HA (100 mg/dm3) under mechanical stirring. The amount of Rh6G or HA adsorbed (qt (mg/g)) was derived from the initial and final concentrations in the liquid phases measured using a UV–Vis spectrophotometer at 524 and 254 nm, respectively, using the following equation:

$$q_{t} = \frac{{\left( {C_{0} - C_{t} } \right).V}}{m}$$
(1)

where C0 and Ct (mg/dm3) are the initial and liquid-phase concentrations at any time t of dye solution (mg/dm3), V (dm3) is the volume of the solution, and m (g) is the adsorbent mass.

The effect of the solution pH on Rh6G dye adsorption was investigated according to the following procedure: 0.2 g of adsorbent was added to 200 cm3 of dye solution (100 mg/dm3) at 20 °C. The initial pH value of dye was adjusted over the range of 2–10 by adding a few drops of diluted NaOH (0.1 mol/dm3) or HCl (0.1 mol/dm3). The adsorbed amounts of dye were determined after 1400 min of an equilibrium time using Eq. 1. Since testing of the kinetics of HA on the composite showed no adsorption, in this case the study of the pH effect is not made.

In binary systems, the experiments were performed at various Rh6G/HA concentrations and following the same procedure as described in the previous paragraph. A correction was applied for the spectrophotometric determination of residual concentrations in mixture systems by using the equations (Zermane et al. 2013; Anirudhan and Ramachandran 2015):

$$C_{\text{Rh6G}} = \frac{{k_{\text{HA2}} d_{1} - k_{\text{HA1}} d_{2} }}{{k_{\text{Rh1}} k_{\text{HA2}} - k_{\text{Rh2}} k_{\text{HA1}} }}$$
(2)
$$C_{\text{HA}} = \frac{{k_{\text{Rh1}} d_{2} - k_{\text{Rh2}} d_{1} }}{{k_{\text{Rh1}} k_{\text{HA2}} - k_{\text{Rh2}} k_{\text{HA1}} }}$$
(3)

where CRh6G and CHA are the concentrations of Rh6G and HA; kRh1, kRh2, kHA1, kHA2 are the calibration constants at 524 and 254 nm; d1 and d2 are the optical densities at the two wavelengths.

Equilibrium adsorption isotherms from single solutions (Rh6G) were obtained by 0.02 g of the composite with 200 cm3 of Rh6G aqueous solutions of various initial concentrations (20–800 mg/dm3) until equilibrium was attained. The adsorption isotherms from binary solutions (Rh6G + HA) were determined using a ratio of dyes concentrations of 1:1 (100:100–300:300 mg/dm3). The same temperature and agitation conditions were considered in all cases. The optimum pH was maintained at 6 for single systems and 3 for binary systems. The amount of dye adsorbed per gram of adsorbent at equilibrium, qe (mg/g), is calculated using Eq. (1) where qt = qe and Ct = Ce. Ce (mg/dm3) is the equilibrium concentration.

Regeneration study

To evaluate the recycling performance of the composite, desorption study was carried out using deionized water. 100 mg/dm3 of Rh6G solution (200 cm3) was treated with 0.2 g of adsorbent for 24 h until adsorption equilibrium. The amount of Rh6G adsorbed is calculated using Eq. 1. The Rh6G-loaded adsorbent was treated with 200 cm3 desorption solution with continuous stirring. After desorption reached equilibrium in 24 h, the adsorbent was separated and it was reused for another adsorption cycle. These experiments were repeated five times.

Results and discussion

Characterization of the adsorbents

N2 adsorption–desorption isotherms are shown in Fig. 1. According to the IUPAC classification, the N2 adsorption of composite and bentonite is of type II with H3 hysteresis, typical of mesoporous solids with slit-shaped pores. The specific surface area for bentonite and composite is, respectively, 74 and 9 m2/g (see Table 2). The molecules of alginates can block the access of gas in the pores to explain the decrease in the textural properties (Huang et al. 2016).

Fig. 1
figure 1

N2 adsorption–desorption isotherms of bentonite and composite

Full size image
Table 2 Textural properties of bentonite and composite
Full size table

X-ray diffraction (XRD) patterns of pure alginate, bentonite, and composite are shown in Fig. 2. Pure sodium alginate has an amorphous morphology (Yang et al. 2012; Ghadiri et al. 2013). It can be observed that bentonite shows some characteristic peaks at 2θ = 6.33° (d001 = 13.95 Å), 19.63° (d003 = 4.51 Å), 34.87° (d006 = 2.57 Å), 62.11° (d060 = 1.63 Å), respectively (Yadav and Rhee 2012). Also, quartz (Q) was detected in the clay sample. When clay was added to alginate, the peaks corresponding to clay mineral crystalline structure were detectable at the same locations of clay alone without any shifting (d001 = 15.06 Å). The fact that the peaks of clay were not shifted by the presence of alginate chains demonstrates that the in situ intercalation of alginate molecules into bentonite layers did not happen. It may conclude that alginate chains were too large and could not be intercalated between the clay mineral layers (Ghadiri et al. 2013).

Fig. 2
figure 2

X-ray diffraction patterns of bentonite materials

Full size image

To elucidate the changes in surface functional groups of the sorbents after encapsulation, a FTIR analysis was carried out (see Fig. 3). No significant differences in hydroxyl (-OH) stretching bands at approximately 3305 cm−1 were observed (Lezehari et al. 2010). Peaks at 1590, 1404, and 1023 cm−1 in pure alginate represent the stretching of COO− (symmetric), COO (asymmetric), and C–O–C, respectively (Ghadiri et al. 2013; Lakouraj et al. 2014). For the bentonite sample, two main peaks were observed at 526 and 1017 cm−1 that correspond to Si–O and Si–O–Si stretching band (Yang et al. 2012; Ghadiri et al. 2013). FTIR spectrum of the composite (see Fig. 3) revealed that the chemical structure of the composite beads was similar to alginate, which was the major fraction in their composition. In composite, the intensity of COO− stretching peak of alginate at 1590 cm−1 decreased and this peak shifted to the higher wavelengths of 1598 cm−1. This effect is probably due to the interactions of silica groups of bentonite with carboxylic groups in alginate that generate hydrogen bonds in the bentonite–alginate composite, and thereby changes the IR absorption of COO− group (Ghadiri et al. 2013).

Fig. 3
figure 3

FTIR spectra of bentonite materials

Full size image

The point of zero charge of an adsorbent is defined as the pH at which the surface charge becomes zero (Anirudhan and Ramachandran 2015). The pHpzc of samples bentonite, alginate, and composite has been determined as 6.66, 6.30, and 6.27, respectively (see Fig. 4). Cation adsorption becomes enhanced at pH higher than the pHpzc, while adsorption of anions is equally enhanced at pH less than pHpzc. An increase in the pH above the point of zero charge tends to increase the adsorption of cationic dyes on the adsorbents (Farahani et al. 2011).

Fig. 4
figure 4

Point of zero charge of bentonite materials

Full size image

Adsorption of Rh6G and HA in single systems

Effect of the pH

The solution pH is an important parameter for the decolorization rate of Rh6G using composite. The results are shown in Fig. 5. It can be seen that the decolorization rate was higher and constant in a wide pH range at basic medium than that obtained under acidic conditions. It has been reported that Rh6G molecule becomes hydrophobic under basic conditions (i.e., at higher pH than its pKa value of 6.13) as the free electron pair on the amine nitrogen (primary amine group) transfers charges from amine nitrogen to aromatic rings and the surface of the adsorbent is negatively charged at a pH above PZC = 6.27. Under such a condition, Rh6G exists in its molecular state and locates itself at the composite interface due to its hydrophobic nature (Rajoriya et al. 2017). Rh6G molecule becomes hydrophilic in nature under acidic pH due to the protonation of nitrogen in the secondary amine group of the xanthene ring (pH < pKa). The electrostatic interaction between Rh6G and the composite resulting from ionized Si–OH was affected by the pH of the solutions. Values of pKa for silica have been reported in the wide range of 3.5–8.2. So, partial ionization of Si–OH could start at a low solution pH (between 3.5 and 6.5), which made the composite surface negatively charged. R6G with a pKa of 6.13 is positively charged during a wide pH range, which favored the electrostatic interaction between composite and Rh6G. It was explained that increasing pH caused the ionization of Si–OH, which provided more electrostatic attraction sites for R6G. Due to its hydrophilic nature, a lower decolorization rate was achieved under acidic conditions (pH < 4) (Rajoriya et al. 2017; Chang et al. 2011). Adsorption tests of humic acid on the composite at various pH values showed that humic acid is not adsorbed.

Fig. 5
figure 5

Effect of the pH for the equilibrium adsorption data of Rh6G on composite (C0 = 100 mg/cm3, T = 23 °C, equilibrium time = 24 h)

Full size image

Kinetic studies

The adsorption kinetics were investigated to determine the equilibrium time for Rh6G and HA sorption on the sorbents. Kinetic curves of Rh6G and HA in single component systems are shown in Fig. 6. The removal of Rh6G was rapid in the initial stages of contact time and gradually decreased with time until equilibrium. The rapid adsorption observed during the first 8 h is probably due to the abundant availability of active sites on the composite or alginate surface, and with the gradual occupancy of these sites, the sorption becomes less efficient (Errais et al. 2011). It appears from the results included in Fig. 6 that the contact time needed to reach equilibrium conditions was 24 h. However, we observe that the amount adsorbed by the composite is greater than that of alginate. So, from these results, our choice is based on the composite to achieve our study. The results also included in Fig. 6 show that HA does not adsorb in the composite. From the results included in Fig. 7, it was clear that the removal of dye was dependent on the concentration of the dye. The adsorption capacity increased with increasing initial dye concentration, and the process was faster at higher concentrations. The shapes of the curves are similar between them and approximately independent of the initial dye concentration.

Fig. 6
figure 6

Kinetic adsorption data for Rh6G and HA in single component systems on composite and alginate (C0 = 100 mg/cm3, T = 20 °C, pH = 6)

Full size image
Fig. 7
figure 7

Kinetic adsorption data for Rh6G on composite at various initial concentrations (m = 200 mg, V = 200 cm3, T = 20 °C, pH = 6)

Full size image

Equilibrium isotherms

The equilibrium isotherms describe how the adsorbent interacts with the adsorbate (Gil et al. 2011). The adsorption of Rh6G on composite was studied under the optimized conditions, and the results are shown in Fig. 8. An isotherm of the type L in Giles classification is obtained (Crini et al. 2009).

Fig. 8
figure 8

Equilibrium adsorption data for Rh6G on composite at pH = 6 (m = 200 mg, V = 200 cm3, T = 20 °C, equilibrium time = 24 h)

Full size image

Adsorption of Rh6G and HA in binary systems

Effect of the pH

In the mixtures, the adsorption of HA was performed at pH = 3. The choice of this pH is based on various works carried out by other authors (Liu et al. 2015; Zhang et al. 2015; Maghsoodloo et al. 2011). They reported the removal of HA from various adsorbents, and they found that the adsorption amount of HA decreased gradually with the increasing pH.

Kinetic studies

The kinetic curves in a mixture system are shown in Fig. 9. The presence of Rh6G improves the adsorption capacity of HA with a synergetic mechanism (see Fig. 9b) (Zermane et al. 2010, 2013). Some phenomena have been advanced to explain this mechanism. Binding between Rh6G and HA is normally suggested for the interaction between cationic dyes and negatively charged molecules. HA is weakly dissociable acids, and a large part of the acid carries predominantly negative charge. Also, Rh6G could attach HA molecules by interacting with their hydrophobic regions since the carbon skeleton of HA molecules contains hydrophobic regions (aliphatic and aromatic components) active in binding organic molecules. HA and Rh6G could consequently form entities that can be adsorbed (Zermane et al. 2013).

Fig. 9
figure 9

Kinetic adsorption data for Rh6G (a) and HA (b) in mixture component systems on composite at various initial concentrations (m = 200 mg, V = 200 cm3, T = 20 °C, pH = 3)

Full size image

Equilibrium isotherms

The adsorption isotherm of Rh6G and HA on composite was studied under the optimized conditions. The results of Rh6G and HA adsorption in binary systems on composite are shown in Fig. 10. The isotherms are of type S in the Giles classification (Crini et al. 2009).

Fig. 10
figure 10

Equilibrium adsorption data for Rh6G and HA on composite (m = 200 mg, V = 200 cm3, T = 20 °C, equilibrium time = 24 h)

Full size image

Kinetics modeling

To characterize the kinetics involved in the process of adsorption, pseudo-first-order, pseudo-second-order and intra-particle kinetic models were proposed, and the kinetic data were analyzed based on the coefficient of determination (R2) and the amount of dye adsorbed at equilibrium.

The pseudo-first-order rate expression of Lagergren based on solid capacity is generally expressed as follows: (Gil et al. 2011; Elmoubarki et al. 2015).

$$\frac{{{\text{d}}q}}{{{\text{d}}t}} = k_{1} \left( {q_{\text{e}} - q} \right)$$
(4)

After integrating and applying the boundary conditions, for q = 0 at t = 0 and q = q at t = t, the integrated form of Eq. 4 becomes:

$$q = q_{\text{e}} \left( {1 - e^{{ - k_{1} t}} } \right)$$
(5)

where qe and q (both in mg/g) are, respectively, the amounts of dye adsorbed at equilibrium and at any time t and k1 (1/min) is the rate constant of adsorption.

The pseudo-second-order model proposed by Ho and Mckay was used to explain the sorption kinetics. This model is based on the assumption that the adsorption follows second-order chemisorption. The pseudo-second-order model can be expressed as:

$$\frac{{{\text{d}}q}}{{{\text{d}}t}} = k_{2} \left( {q_{\text{e}} - q} \right)^{2}$$
(6)

After integrating for the similar boundary conditions, the following equation can be obtained:

$$q = \frac{{k_{2} q_{\text{e}}^{2} }}{{1 + k_{2} q_{\text{e}} t}}$$
(7)

where k2 (g/mg min) is the rate constant of pseudo-second-order adsorption.

The intra-particle diffusion was explored by the following equation:

$$q = k_{\text{id}} t^{1/2} + C$$
(8)

where kid is the intra-particle diffusion rate constant (mg/g min1/2) and C (mg/g) is a constant.

The adsorption’s kinetic parameters in single and binary systems were estimated by nonlinear regression (see Tables 3, 4). The regression coefficients for the pseudo-first-order and pseudo-second-order equations for the adsorption of Rh6G were found to be higher than 0.96. A comparison of these results with the experiment suggests that the first-order model is more reasonable than the second-order one. The same conclusions were found by Benhouria et al. (2015) in the case of the adsorption of BM onto calcium alginate–bentonite–activated carbon composite and Djebri et al. (2016) in the case of the adsorption of BM onto calcium alginate–organobentonite composite. The experimental data were also fitted to the intra-particle diffusion model (R2 > 0.9). As depicted in Table 3, the adsorption of Rh6G onto bentonite–alginate composite consists of two different steps, including intra-particle or pore diffusion and the equilibrium stage (Elmoubarki et al. 2015).

Table 3 Pseudo-first-order and pseudo-second-order parameters for Rh6G adsorption by composite at various initial concentrations (m = 200 mg, V = 200 cm3, T = 20 °C, pH = 6)
Full size table
Table 4 Pseudo-first-order and pseudo-second-order parameters for Rh6G and HA adsorption by composite in binary systems at various initial concentrations (m = 200 mg, V = 200 cm3, T = 20 °C, pH = 3)
Full size table

Equilibrium analysis

In this study, the nonlinear Langmuir isotherm model (Table 5) was established to analyze the equilibrium data. In the Langmuir equation (see Eq. 9), qm denotes the maximum adsorption capacity, corresponding to a monolayer coverage, and KL is a constant related to the energy of adsorption (Ely et al. 2011; Santos and Boaventura 2016). The parameters obtained are shown in Table 5, and the model curve is illustrated in Fig. 10a.

Table 5 Langmuir parameters for Rh6G adsorption by composite. T = 20 °C, pH = 6
Full size table
$$q_{\text{e}} = \frac{{q_{\text{m}} K_{\text{L}} C_{\text{e}} }}{{1 + K_{\text{L}} C_{\text{e}} }}$$
(9)

This model may be used to estimate the maximum uptake although it cannot provide a mechanistic understanding of the sorption process. The coefficients of determination (R2) indicate a good correlation between the experimental data and the model. The maximum adsorption capacity is 429.5 mg/g. On the basis of these results, it can be said that the Langmuir model is adequate for a good description of this isotherm of adsorption. Similar results were reported by Nessma et al. (2016) in the case of the adsorption of BM onto calcium alginate–organobentonite composite in aqueous solutions.

Reusability

The regeneration of the pollutant loaded on the adsorbent makes the adsorption process more economic and cost-effective (Dalvand et al. 2016). The results are presented in Fig. 11. This figure shows the efficiency of composite for dye removal after five cycles decreases from 48.62 to 33.22 mg/g. This result indicates that the synthesized adsorbent, as a reusable adsorbent, can repeatedly be applied for dye removal.

Fig. 11
figure 11

Reuse of composite (C0 = 100 mg/cm3, m = 200 mg, V = 200 cm3, T = 20 °C, pH = 6)

Full size image

Conclusions

In this study, the modification of the clay surface by the introduction of a biopolymer resulted in an enhancement of the adsorption capacity of the resulting composite. Sorption experiments were performed using rhodamine 6G (Rh6G) and humic acids (HA). Composite is a good adsorbent for Rh6G and HA both in single and binary systems. In the single systems, Rh6G adsorption was affected by the solution pH and the concentration. Higher pH will generally result in higher adsorption capacities. In the binary mixtures, the presence of Rh6G improves the adsorption capacity of HA with a synergetic mechanism. The pseudo-first-order kinetic model describes the experimental data. Langmuir isotherm fits well with the results obtained for the sorption of Rh6G. The obtained maximum adsorption capacity at 20 °C and pH = 6 was 429.49 mg/g. To summarize, it could be concluded that composite is an efficient and reusable adsorbent which can be successfully applied for dye removal from an aqueous environment.