Introduction

Groundwater is very important in day to day life for people and society (Shigut et al. 2017). It has not only been used for supplying potable water to both urban and rural areas but also essential for irrigation, economic development, and protection of environmental and ecological balance (Cheng and Fanhai 2012, Srinivas et al. 2015, Kumar et al. 2015, Al-Ahmadi 2013). Recently, providing good quality water for drinking is considered a fundamental requirement for public health protection. Consequently, the poor quality of water may threaten human health and plant growth (Zhu et al. 2014, Hosseini-Moghari et al. 2015). Most water contamination originates from the disposal of solid wastes from different human activities, such as agriculture, construction and industry, and the disposal of domestic and industrial wastewater is discharged into rivers through the sewer systems (Li et al. 2015, Zhang et al. 2015, Kumar et al. 2016). These systems may often leak wastewater into shallow aquifers, directly or indirectly and groundwater supplies from nearby wells are affected if they are exposed to these wastewater pollutants (Li et al. 2016, Qishlaqi et al. 2017, Pinto 2015).

When groundwater is polluted, its quality cannot be restored by stopping the contaminants from the sources. Shallow, unconsolidated aquifers are particularly vulnerable to contamination, which may persist in groundwater for many years or decades (Li et al. 2016, Liu et al. 2010). Meanwhile, it becomes necessary to monitor the groundwater quality regularly and devise ways to protect it (Kaur et al. 2014, Shigut et al. 2017). In the study area, the shallow aquifer in the Quaternary Unconsolidated Sedimentary Basin, the largest source of drinking water in the North Chengdu plain, China, is, however, constantly impacted by agriculture, industry, mining, and other human activities. This has challenged the water resource managers and forced them to pay attention to the evaluation of groundwater contamination in the study area based on the recognized assessment methods.

At present, many methods are available at home and abroad, and proven to be powerful in water quality assessment, such as the principal component analysis (Gangopadhyay et al. 2001), neural network model (Wu et al. 2007), Bayesian discrimination method (Chen et al. 2009), entropy method (Chun-rong and Jun 2011), water pollution index method (Liu et al. 2013), grey clustering method (Zhang 2014), statistical analysis method (Liu et al. 2015) and others. However, these methods cannot directly reflect pollution characteristics, and the linear relationship between those variables may have some effects on the results (Li et al. 2018). In the same vein, the methods above have their own merits, but they are less feasible and challenging to popularize in the regional groundwater pollution assessment due to the complex and changeable environmental problems. Furthermore, in all environmental quality assessments, there is uncertainty about environmental risk, because of inconsistency and peculiarities of each groundwater pollutant.

To overcome the shortcomings associated with the above methods and respond to the call of water resource managers, fuzzy mathematics evaluation (FME) method was used. FME method has a large range of applications which could help in identifying and overcoming any uncertainty regarding the risk of groundwater contamination using membership functions (Mujumdar and Sasikumar 2002, Ma et al. 2010, Zhang et al. 2012, Kamrani et al. 2016). It has also been proven effective to deal with complex and changeable environmental problems (Singh et al. 2017), and also controlling the effect of monitoring errors on assessment results (Ghasemi et al. 2014).

This study is considered as the first of its kind to assess groundwater quality in this region and nearby surrounding. To show the advantage of FME, it was compared with Comprehensive Evaluation Method (CEM), which is the most common method of assessing the quality of groundwater for drinking in China, and recommended by the quality standard for groundwater of China (GB/T 14848-93) (Wu and Sun 2016, Su et al. 2017). This method provides a holistic view of groundwater quality status and appropriateness for drinking purposes by considering various water quality parameters based on simple mathematical-numerical tools. Therefore, the aims of this study are: (1) evaluating groundwater quality condition and its suitability for drinking purposes in the Quaternary Unconsolidated Sedimentary Basin, (2) identifying the main pollutants which influence the groundwater quality and (3) compare the evaluation results to learn about the technique characteristics of the evaluation methods used. Therefore, this study will be an essential reference for future studies. It will also be useful for the local decision makers in regional groundwater management and protection.

Materials and methods

Description of study area

The study area is located between longitudes 103°54′02″ to 104°16′54″ and latitudes 30°40′40″ to 30°57′58″ in the North Chengdu Plain and bounded by many rivers, which are tributaries of the Minjiang river and is divided into many villages with the total population of over 140,000. The primary source of drinking water and agricultural irrigation in the study area is groundwater from the Unconsolidated Quaternary sediments, which provides water to residents. It has a sub-tropical humid monsoon climate with four seasons. Compared to other areas in the same climatic zone, features such as low temperature, less sunshine, and rainy weather are more frequent. The mean annual temperature is 10.4 °C, the average temperature of coldest months and the hottest month is 4.6 and 24.4 °C, respectively. The region is dominated by NW wind, with a maximum wind speed of 17 m/s and average wind speed of 1.3 m/s. No typhoons are observed. The annual maximum relative humidity is 80%, and the minimum relative humidity is 75%. The annual maximum of absolute moisture content is 15.2, and the minimum is 14.3. Rainfall is the main recharge source of groundwater. The average annual precipitation is 1134.8 mm. Moreover, the longest continuous period of rainfall is 28 days. The Longqiao water plant has been established on the right bank of the Pi river at a distance of 38 m. The daily production capacity of the Longqiao water plant is about 10,000–12,000 m3/d, and the daily water supply is 8000–10,000 m3/d. However, the groundwater is exposed to the risk of contamination from different sources. The main pollution sources of groundwater in the study area comes from the domestic sewage water, and industrial wastewater discharged routinely into the Pi river, which is estimated at 8.4 × 103 m3/d and agricultural pollution from using chemical fertilizers and pesticide. It is believed that most of the wastewater is infiltrated into the shallow aquifer in the Quaternary Unconsolidated Sedimentary Basin in the area, because of its shallow depth of the groundwater level (2.0–10 m) and relatively high hydraulic conductivity (k = 10–50 m/day). So, it is necessary to evaluate the quality of drinking water in this region since it is closely linked to people’s health.

Sample collection and analysis

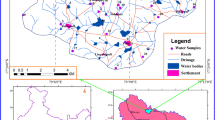
In this study, groundwater samples were obtained from six monitoring wells (S1, S2, S3, S4, S5, and S6) from the shallow aquifer in the Quaternary Unconsolidated Sedimentary Basin near the Pi river, China. These six monitoring wells are located between the Pi river and Longqiao drinking water supply plant. The locations of groundwater samples are displayed in (Fig. 1). The sampling wells (S1, S2, and S3) are inside the wall of Longqiao water plant, while the sampling wells (S4, S5, and S6) outside the Longqiao water plant wall. Well (S2) is near the septic tank of the plant workers, and the wells (S1 and S3) are near the management offices and workers residences, respectively. Whereas, the well (S4) is near the Pi river bridge and the sampling wells (S5 and S6) are in the middle of farms existing in the area. These wells are used as a group in the Longqiao water plant to provide supply drinking water to residents in the Longqiao town and its surrounding area. It was observed that the location of wells is exposed to the risk of groundwater pollution resulting from the domestic sewage water and industrial wastewater discharged into the Pi river. Also, unsuitable use of agricultural chemicals, unhealthy open defecation and many more potentially infiltrate into the shallow aquifer. This built the foundation for selecting the location for research samples to evaluate because they have relative importance as source of drinking water in the region. The samples were collected after 10 min of pumping and stored in clean 500-mL glass bottles that were thoroughly washed with detergent and rinsed with deionized water. The samples were sent to the laboratory of Environmental Engineering Center of Sichuan Geological Engineering Investigation and kept in a refrigerator at a temperature below 4 °C until analyzed. pH and total dissolved solids (TDS) were measured in situ using a portable pH and TDS meters because the parameters are likely to change during transport. Water sampling methods were according to (Kent and Payne 1988). The samples were analyzed for 19 various physicochemical parameters, include hydrogen ion concentration (pH), total hardness (TH), total dissolved solids (TDS), potassium (K+), sodium (Na2+), calcium (Ca2+), magnesium (Mg2+) sulfates (\({\text{SO}}_{4}^{2 - }\)), chlorides (Cl−), bicarbonates (\({\text{HCO}}_{3}^{ - }\)), potassium permanganate index (CODMn), nitrate (\({\text{NO}}_{3}^{ - }\)), nitrite (\({\text{NO}}_{2}^{ - }\)), ammonia (\({\text{NH}}_{4}^{ + }\)), iron (Fe), manganese (Mn), arsenic (As), chromium (Cr6+), and lead (Pb). These parameters were used as index indicators to evaluate the groundwater contamination risk in the study area. This selection was based on their importance to the water quality and the potential impact on human health and their pollution potential on groundwater resource in particular (Zhang et al. 2017). Detection methods for each parameter were as follows: the concentrations of K+ and Na+ were measured using flame photometer. TH, Ca2+, Mg2+, Cl−, and \({\text{HCO}}_{3}^{ - }\) were analyzed by titrimetric methods. The concentrations of CODMn, \({\text{NH}}_{4}^{ + }\), \({\text{NO}}_{3}^{ - }\), \({\text{NO}}_{2}^{ - }\), and \({\text{SO}}_{4}^{2 - }\) were determined using spectrophotometer technique. And finally, the Fe, Mn, As, Cr6+, and Pb concentrations were then measured using atomic absorption spectrometry.

Fig. 1
figure 1

Location of study area and groundwater samples

Full size image

In this study, the groundwater suitability for drinking and domestic purposes was evaluated by complying the values of various groundwater quality parameters according to China’s Quality Standards for Groundwater (GB/T14848-93), since it is the only way to assess groundwater quality in China by specifying the classification of groundwater quality, groundwater quality monitoring, evaluation methods and groundwater quality protection (Chinese 1993). It also corresponds to the methods applied to assess the quality of groundwater in this paper by dividing the groundwater quality into five categories: excellent, good, moderate, poor and very poor.

Principle for fuzzy mathematics evaluation method

Fuzzy mathematics was proposed by Zadeh in 1965 (Mahapatra et al. 2011, Zhang et al. 2009) as a new way to represent vagueness in everyday life. This method is proven to be capable of dealing with complex systems under uncertain and imprecise conditions (Gharibi et al. 2012, Singh et al. 2017). Risk assessment of groundwater contamination could be a challenge because it often involves many groundwater quality parameters. Fuzzy mathematics can simplify this risk assessment process (Zhang et al. 2012). It takes the effectual measurement of pollutant concentration compared with its evaluation criteria. Through accepted linear function, it calculates each pollution element of membership on the level of groundwater contamination. Afterwards, fuzzy matrix can be set, and the weight of each single element value can be obtained by calculation, which constitutes the weight factors matrix. Last, the membership matrix and the weight factors matrix are multiplied, and the evaluation results can be derived (Agoubi et al. 2016, Feng et al. 2012). Figure 2 shows the steps of creating the fuzzy mathematics model.

Fig. 2
figure 2

Flow chart of the fuzzy mathematics method

Full size image

Determining the evaluation factors

Depending on the circumstances of environment, the evaluation factors set U = (u1, u2,…,u n ) = (pH, TH, TDS, \({\text{SO}}_{4}^{2 - }\), Cl−, CODMn, \({\text{NO}}_{3}^{ - }\), \({\text{NO}}_{2}^{ - }\), \({\text{NH}}_{4}^{ + }\), Fe, Mn, As, Cr6+, and Pb), which represent the overall situation of groundwater quality of the Quaternary Unconsolidated Sedimentary Basin. The element u (i =1, 2,…n) is measured value of pollutants that affect the quality of groundwater.

Determining the evaluation standard

This paper adopts the Chinese national standards of groundwater quality (GB/T 14848-93) as the evaluation standard, which was drafted by the Ministry of Geology and Mineral Resources of the People’s Republic of China. Based on groundwater quality in China and human health requirement as well as the objective of water protection, the standard (GB/T 14848-93) classifies groundwater quality into five grades (I, II, III, IV, and V). The quality evaluation grades of water V =(v1, v2,…v m ) are represented by v i (i =1, 2,…m), and it is the standard classification value of groundwater for any contamination, which includes five levels: excellent (grade I), good (grade II), moderate (grade III), poor (grade IV), and very poor (grade V). Groundwater with grades I and II is of excellent and good quality and is suitable for all uses. Grade III is moderate-quality water, which is generally suitable for drinking, irrigation, and industrial production. Grade IV is poor quality water, which is fit only for irrigation and industrial production and may be used for drinking after proper treatment. Grade V groundwater is very poor quality water that cannot be used for any purpose (Chinese 1993). The classification of these grades about each evaluation factor is given in Table 1.

Table 1 Classification of groundwater quality based on the Chinese national standard (GB/T 14848-93)
Full size table

Determining the weights of factors

The weights of factors are important elements in the mathematical model of FME technique, which reverses the position and role of each factor in the measures of comprehensive decision making, and the result of the comprehensive evaluation is directly affected by it. The equations for weight is as follows (Zhang 2014):

$$W_{i} = \frac{{C_{i} }}{{S_{i} }},$$
(1)
$$S_{i} = \frac{1}{n}\sum\limits_{j = 1}^{n} {\alpha_{ij} } ,$$
(2)

where C i is the measured values of index i, S i is the standard value for index i, n is the grading number of water quality standard, and α ij is the jth sample value under the ith level of classification factor. To make the fuzzy compositional operation, the weight of each single factor must be normalized as follows:

$$\overline{{W_{i} }} = \frac{{C_{i} }}{{S_{i} }} \times \frac{1}{{\sum\limits_{i = 1}^{n} {\frac{{C_{i} }}{{S_{i} }}} }},$$
(3)

where \(\overline{{W_{i} }}\) represents the normalized weight of the evaluated index i.

Based on the above equation, the weight set of the single factor can be determined \(A = \{ \,\overline{w}_{{_{1} }} ,\overline{w} {}_{2}, \ldots \,\overline{w} {}_{i}\} .\)

Determination of the membership and relation matrix R

A fuzzy set is completely characterized by its membership function (MF). The (MF) has been used to assess groundwater quality according to the standards. The level of membership belongs to a type of fuzzy information which overcomes the differences among water index grade standards in different places (Zhang 2014). The FME begins with the concept of a fuzzy set. The fuzzy set describes the relationship between an uncertain quantity (x) and a membership function (μ). The elements of fuzzy set membership may be described as a number in the interval [0, 1] (Nasr et al. 2012). The greater the value of membership, the higher the membership qualifications. When the value of membership is 1, it is subordinated completely, and when the value of membership is 0, it is subordinated incompletely. The membership degree of the fuzzy set is defined over a domain X which takes the form:

$$\mu_{A} {\kern 1pt} {\kern 1pt} :X \to \left[ {0,1} \right],$$
(4)

where each element of X is mapped to a value between 0 and 1. This value is referred to as membership value or degree of membership, and it is used to determine the degree of membership of each rating factor. Hence, the fuzzy set A is defined by its MF:

$$\mu_{A} (x) = \left\{ {\left( {\mu_{A} (x)} \right),x \in X,\mu_{A} (x) \in \left[ {0,1} \right]} \right\}.$$
(5)

The membership function sets are represented through triangular, trapezoidal, Gaussian, Pseudo exponential, Sigmoidal and other shapes of fuzzy numbers (Miao et al. 2014, Srinivas et al. 2017). Generally, water quality parameter’s impact is represented by certain range of values, and the firing level of the conclusion is computed as the product of dismissal levels from the antecedent (Agoubi et al. 2016). In this study, the triangular membership function is used to normalize the crisp inputs because of its simplicity and computational efficiency and provide an environment more conductive to human-in-the-loop knowledge acquisition (Mahapatra et al. 2011, Caniani et al. 2015). It can be represented mathematically for any of the fourteen groundwater quality parameters with respect to five classification grades (I, II, III, IV, and V) as follows (Lermontov et al. 2009):when j = 1,

$$\mu_{A} \left( x \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & {x \le \alpha_{ij} } \hfill \\ {\frac{{\alpha_{{_{ij + 1} }} - x}}{{\alpha_{ij + 1} - \alpha_{ij} }}} \hfill & {\alpha_{ij} < x < \alpha_{ij + 1} } \hfill \\ 0 \hfill & {x > \alpha_{ij + 1} } \hfill \\ \end{array} } \right.,$$
(6)

when j = 2, 3, 4

$$\mu_{A} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {x < \alpha_{ij - 1} } \hfill \\ {\frac{{\alpha_{{_{ij + 1} }} - x}}{{\alpha_{ij + 1} - \alpha_{ij} }}} \hfill & {\alpha_{ij} \le x < \alpha_{ij + 1} } \hfill \\ {\frac{{x - \alpha_{{_{ij - 1} }} }}{{\alpha_{ij} - \alpha_{{_{ij - 1} }} }}} \hfill & {\alpha_{ij - 1} \le x < \alpha_{ij} } \hfill \\ 0 \hfill & {x < \alpha_{ij + 1} } \hfill \\ \end{array} } \right.,$$
(7)

when j = 5

$$\mu_{A} \left( x \right) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {x < \alpha_{ij - 1} } \hfill \\ {\frac{{x - \alpha_{{_{ij - 1} }} }}{{\alpha_{ij} - \alpha_{ij - 1} }}} \hfill & {\alpha_{{_{ij - 1} }} < x < \alpha_{ij} } \hfill \\ 1 \hfill & {x \ge \alpha_{ij} } \hfill \\ \end{array} } \right.,$$
(8)

\(\alpha_{ij} ,\alpha_{{_{ij + 1} }} \;{\text{and}}\;\alpha_{ij - 1}\) are the different levels of groundwater quality standards and \(x\) is the real measured concentration of each factor.

The membership function can be described of five twin grades and the fuzzy relationship matrix R is formed as follows:

$$R = \left[ {\begin{array}{*{20}l} {r_{11} } \hfill & {r_{12} } \hfill & \cdots \hfill & {r_{1m} } \hfill \\ {r_{21} } \hfill & {r_{22} } \hfill & \cdots \hfill & {r_{2m} } \hfill \\ \vdots \hfill & \vdots \hfill & {} \hfill & \vdots \hfill \\ {r_{n1} } \hfill & {r_{n2} } \hfill & \cdots \hfill & {r_{nm} } \hfill \\ \end{array} } \right].$$
(9)

Fuzzy evaluation of groundwater quality

The fuzzy evaluation matrix B for groundwater quality evaluation is obtained by the compositional process of the weight A and the fuzzy evaluation matrix R of each single grade for I, II, III, IV, and V respectively. The principle of FME method can be described by the mathematical Eq. (10), with the main purpose of weighting evaluation factors (Hao et al. 2012).

$$B = A \times R = \{ \,\overline{w}_{1} ,\overline{w} {}_{2}, \ldots \overline{w} {}_{i}\} \times \left[ \begin{aligned} r_{11} {\kern 1pt} {\kern 1pt} {\kern 1pt} \quad r_{12} \quad \cdots \quad r_{1m} \hfill \\ r_{21} {\kern 1pt} \quad {\kern 1pt} {\kern 1pt} r_{22} \quad \cdots \quad r_{2m} \hfill \\ {\kern 1pt} {\kern 1pt} \vdots \quad \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \vdots \quad \quad \quad \quad \vdots \hfill \\ r_{n1} \quad {\kern 1pt} {\kern 1pt} {\kern 1pt} r_{n2} \quad \cdots \quad r_{nm} \hfill \\ \end{aligned} \right]$$
(10)

From the principle of maximum membership, the grade of groundwater quality is determined.

Comprehensive evaluation method

The comprehensive evaluation method (CEM) is based on the classification of individual component to determine the quality category required as in Table 2 to determine the individual component evaluation score of Fi, and press the comprehensive evaluation to determine the value of F. The evaluation is carried out using the quality standard for groundwater of China (GB/T 14848-93) as classified in the FME technique. (Chinese 1993). As per standard, CEM can be computed as follows (Su et al. 2017):

$$F = \sqrt {\frac{{\overline{{F^{2} }} + F^{2}_{\hbox{max} } }}{2}} \quad (i = 1,2,3, \ldots n),$$
(11)
$$\overline{F} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {F_{i} } \quad (i = 1,2,3, \ldots n),$$
(12)

where n denotes the number of indices selected for the assessment, F is the value of CEM for a given sample, and F i represents the assigned value for the ith index by the quality standard for groundwater (GB/T 14848-93). \(\overline{F}\) is the average value of each individual component score of F i , and (F i )max is the maximum value of the individual component evaluation score F i . Once F is determined, groundwater quality classification can be obtained as per the criteria in Table 3 (Wu and Sun 2016).

Table 2 Individual component classification
Full size table
Table 3 Standards of the groundwater quality classification
Full size table

Results and discussion

Groundwater quality parameters

The concentration values of groundwater quality parameters obtained from the six wells in the study area were statistically analyzed. It should be noted that for each well, four samples were taken at different periods and there was no apparent change in the analysis results of these samples and, therefore, it was taken as the average. The results represented as maximum, minimum, mean and standard deviation for the main groundwater quality parameters are shown in Table 4. Their levels were compared with the acceptable limits recommended by the national quality standards for groundwater of China (GB/T 14848-93) to see if they were suitable for drinking.

Table 4 Descriptive statistics of groundwater quality variables for six sampling wells in the study area
Full size table

As shown in Table 5, the pH of the groundwater is within the range of 6.7–7.5 with the mean of 7.27, indicating that the groundwater in the study area is slightly alkaline for most of the groundwater samples. All samples fall within limits (6.5 and 8.5) of quality standard for groundwater of China (GB/T 14848-93). The average concentrations of water K+, Ca2+, Mg2+, and \({\text{HCO}}_{3}^{ - }\) were 2.018, 92.34, 17.23, and 299.0 mg/L, respectively, and no limits set for these parameters have been stated of quality standard for groundwater of China (GB/T 14848-93). The Na+ concentration was determined between 6.00 and 12.00 mg/L with an average of 9.417 mg/L. All samples of groundwater are found below the permissible limit of (GB/T 14848-93). The concentrations of TH and TDS range from 260.20 to 355.30 mg/L and 331.80 to 415.40 mg/L, with an average of both 301.50 and 368.97, respectively. This indicates that the quality of all groundwater in the study area is classified as very hard to TH and fresh water to TDS, respectively, according to (Todd 1980, Sawyer and McCarty 1967). In this study, the concentrations of (TH and TDS) are found below the allowable limit of (GB/T 14848-93) for all groundwater samples. At the same time, the concentrations of \({\text{SO}}_{4}^{2 - } ,\) Cl−, CODMn, \({\text{NO}}_{3}^{ - } ,\) \({\text{NO}}_{2}^{ - } ,\) and \({\text{NH}}_{4}^{ + }\) in groundwater range from 52.83 to 68.20, 15.96 to 20.92, 0.23 to 0.29, 1.17 to 3.96, 0.003 to 0.005 and 0.020 to 0.68 mg/L, respectively, with a cumulative average for each concentration of 60.22, 17.61, 0.25, 2.40, 0.004 and 0.14 mg/L, respectively. The values of these concentrations for all the groundwater samples collected in this study are within the permissible limit of (GB/T 14848-93) for groundwater quality except sample S2 of \({\text{NH}}_{4}^{ + }\) which exceeds the acceptable limit of 0.2 mg/L according to the national quality standards for groundwater (GB/T 14848-93). Finally, the concentrations of Fe, Mn, As, Cr6+, and Pb in groundwater were 0.086–0.23 mg/L with the mean 0.59 mg/L, 0.01–0.21 mg/L with a mean of 0.07 mg/L, 0.0002–0.0002 mg/L with the mean 0.0002 mg/L, 0.002–0.004 mg/L with a mean 0.003 mg/L and 0.005–0.01 mg/L with an average of 0.008 mg/L, respectively. Among them, Fe and Mn are found to exceed the permissible limits of drinking water as set by (GB/T 14848-93) of 0.3 and 0.1 mg/L, respectively, and remaining concentrations fall within the permissible limits of (GB/T 14848-93) for all groundwater samples. For Fe concentration, two samples exceed the permissible limit represented in sites (S2, S4) and for Mn concentration, one sample exceeds the permissible limit at the site (S2). According to the mean values, the dominance of cations is Ca2+ > Mg2+ > Na+ > K+ and anions is \({\text{HCO}}_{3}^{ - }\) > \({\text{SO}}_{4}^{2 - }\) > Cl−, which makes the predominant type of groundwater to be Ca–Mg-HCO3 type. As mentioned above, the groundwater quality indicators exceeding the standard ratio in the study area were mainly Fe, Mn, and NH4 for sampling points S2 and S4 (Fig. 3).

Table 5 The weight value of groundwater quality parameters in well No. S2
Full size table
Fig. 3
figure 3

Groundwater quality indicators exceeding the standard ratio in the study area

Full size image

Fuzzy mathematics evaluation results of study area

According to the above-mentioned relevant principles of the FME technique for the assessment of groundwater quality of the study area, the steps for evaluation results can be listed as follows:

Evaluation factors

In this study, a FME technique was used to assess the groundwater quality of the quaternary unconsolidated sedimentary basin near the Pi river according to quality evaluation parameters and five classifications of groundwater quality based on the Chinese national standard (GB/T 14848-93) (Table 1). The groundwater quality was assessed for six wells (S1, S2, S3, S4, S5, and S6) as selected in the study area. Of the 19 groundwater parameters analyzed, 14 parameters (pH, TH, TDS, SO4, Cl, CODMn, NO3, NO2, NH4, Mn, Fe, As, Cr6+ and Pb) were selected due to the fact the rest did not have the five-level division as required in the China’s standard for groundwater quality evaluation (GB/T 14848-93). This selection is also based on the fact that it is periodically monitored by the Local Environmental Protection Department for their vital importance to the water quality and potential influence on human health.

Weight of each evaluation factors

According to Eqs. (1) (2) and (3), the corresponding weight values of all wells in the study area were obtained, using the (GB/T14848-93) standard (Table 1) and data from Table 4 for the fourteen selected indicators. The weight values for well No. S2 are shown in Table 5, as an example.

The membership and relation matrix of different evaluation factors on various grades

Based on Eqs. (6) (7) and (8), the degree of membership of each indicator to the groundwater quality grade is calculated. Each indicator is computed to have five levels of membership, and the fourteen selected indicators can get fourteen sets of numerical values. Accordingly, the corresponding fuzzy relationship matrix R is achieved from the selected indicators of all wells in the study area which was computed. The membership for well No. S2 is shown in Table 6, as an example.

Table 6 Membership of well No. S2
Full size table

This membership can be expressed by fuzzy relationship matrix, as follows:

$$R = \left[ {\begin{array}{*{20}c} 0 & {0.20} & {0.80} & 0 & 0 \\ 0 & {0.998} & {0.002} & 0 & 0 \\ {0.63} & {0.37} & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ {0.56} & {0.44} & 0 & 0 & 0 \\ 0 & 0 & 0 & {0.1} & {0.9} \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & {0.88} & {0.12} & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ \end{array} } \right].$$

Fuzzy evaluation of groundwater quality

Based on Eq. (10), the fuzzy evaluation matrix B for groundwater quality evaluation was obtained by the compositional process of the weight matrix A and the fuzzy evaluation matrix R. For example, the fuzzy evaluation matrix B of the well No. S2 is as follows:

$$B = \left( {0.076, \, 0.136, \, 0.141, \, 0.036, \, 0.611} \right).$$

According to the principle of maximum membership to determine the groundwater quality level, 0.611 is the maximum of all five values. Therefore, well No. S2 was found to belong to grade V, which is classified as very poor and their water quality cannot be used for any purpose. The degradation in groundwater quality at this well is mainly due to high concentrations of NH4 and Fe (see Table 6). Similarly, the groundwater quality grades of the other wells in the study area were obtained. The results are shown in Table 7.

Table 7 The fuzzy evaluation of groundwater quality
Full size table

From Table 7 and Fig. 4, the results of fuzzy evaluation matrix B for the other wells showed that the groundwater quality of well No. S1 is (0.579, 0.421, 0, 0, 0), and it found to belong to grade I, which is classified as excellent and their water quality is considered to be suitable for various purposes. The groundwater quality of wells No. S3 is (0.379, 0.477, 0.144, 0, 0), and categorized as being grade II, which is classified as good, and was also deemed to be suitable for all uses. Finally, the groundwater quality of wells No. S4, S5 and S6 are (0.264, 0.239, 0.466, 0.032), (0.214, 0.318, 0.468, 0, 0), (0.207, 0.319, 0.473, 0, 0), respectively, which fall under grade III and is classified as moderate, and their water quality is generally suitable for drinking, irrigation, and industrial production. From the six groundwater samples, grade I of groundwater occupies 16.67%, grade II 16.67% and grade III 50% that means about 83.33% of the groundwater samples could be used as drinking water source. However, S2 is grade V (16.67%), which cannot be used for drinking. This suggests that the groundwater quality in the study area, in general, is not bad. Through analysis of the water indicators, the elevated groundwater quality indicators were mainly NH4, Fe, and Mn which have resulted in the evaluation of well No. S2 as class V which is very poor.

Fig. 4
figure 4

Comprehensive assessment of fuzzy technique for assessing groundwater quality

Full size image

According to our field investigation in the study, the very poor groundwater quality of well No. S2 could be attributed to several reasons:

  1. 1.

    In the Basin of Minjiang as Pi river is a tributary of Minjiang river, sediment has a certain amount of Fe and Mn under the natural environmental conditions (Zeng Jichuan 2009, Li et al. 2006). Thus, the over-limit ratio of Fe and Mn is considered natural environment.

  2. 2.

    The sample No. S2 was taken from the water plant, which is closest to the populated area, and the infiltration of the plant domestic wastewater may lead to the increase of NH4 content. In essence, the groundwater quality of the well S2 is mainly influenced by human activities.

  3. 3.

    Excessive discharge of industrial waste water and domestic sewage is the main cause of groundwater pollution in the study area. Considering the aforementioned reasons, well No.2 is deemed contaminated and, therefore, should be monitored periodically and protected from the causes of pollution to avoid being consumed by local residents.

Groundwater quality evaluation based on comprehensive evaluation method

In the study area, groundwater is a vital source of drinking water for residents. The CEM has been used to assess the quality of groundwater of the Quaternary Unconsolidated Sedimentary Basin near the Pi river and to demonstrate the advantage of this study. In this method, the same physicochemical water quality parameters that were chosen in the FME method (14 parameters) have been used for six wells (S1, S2, S3, S4, S5, and S6). The results are shown in Table 8. As shown in Table 8 and Fig. 5, F values of all analyzed samples in the study area differ from 0.82 to 7.29, ranging from good quality to very poor quality. The results of the assessment showed that four groundwater samples (66.67% of all samples) are classified as good quality water (grade II) which is suitable for various purposes. Two groundwater samples (33.33% of all collected samples) are classified as poor and very poor quality water (grade IV and V), respectively, which are classified as unsuitable for drinking. The common contaminants in these samples are NH4, Fe, and Mn, which are mainly from the natural environment, industrial and agricultural activities. According to the results of the CEM, four groundwater samples (S1, S3, S5, and S6) could be used as drinking water source, while (S2 and S4) cannot be used as drinking water source.

Table 8 Groundwater quality classification based on comprehensive evaluation method
Full size table
Fig. 5
figure 5

Results of groundwater quality evaluation based on comprehensive evaluation method

Full size image

Comparison between fuzzy mathematics evaluation technique and comprehensive evaluation method

The present study analyzed groundwater quality status of six wells in the Quaternary Unconsolidated Sedimentary Basin using FME technique and CEM. Based on the results of the assessment obtained from both methods, the holistic picture of groundwater quality within the study area was satisfactory and consistent with the actual situation of the study area under the prevailing conditions. The indices for both methods indicated that the groundwater quality in the study area was suitable for drinking at ratio 83.34 and 66.67%, respectively. The FME showed only the well No. 2 to be unsuitable for drinking water (see Table 7), while the CEM showed wells No. 2 and 4 to be unsuitable for drinking water (see Table 8). This is due to the technical difference of both methods. For instance, the FME approach uses membership degree to describe the limit between different pollution degrees for assessing groundwater quality. The FME technique takes into account the impression of each assessment factor on the evaluation result and determines the major pollutants according to the weights of evaluation factors. This reflects how close the actual concentration of boundary water quality index of water quality is, hence making the evaluation more comprehensive and reasonable. Whereas, the CEM of water highlights the largest factor of pollution as the index classification is based on the binary logic. Therefore, they cannot describe the continuity of environmental quality, and cannot objectively reflect the influence of the index value near the water quality grade limit for quality evaluation and classification.

Despite the FME and CEM generated almost similar results to the holistic picture of groundwater quality in the study area, the fuzzy indicator is recommended as the more useful indicator for the following advantages:

1. Ability to describe a wide variety of non-linear relationships. 2. They tend to be simple since they are based on a set of local simple models. 3. Fuzzy mathematics can deal with and process missing data without compromising the final result. 4. Avoiding artificial precision as well as generating results which are more consistent with the ecological complexity of real-world issues. 5. Combining both qualitative and quantitative information to express the ecological status of the case study, which is a unique capability of fuzzy approach.

In general, the results revealed that the knowledge-based models such as FME method were practical and flexible tools for incorporating the experts’ attitudes and modeling the current uncertainties associated with water resources and environmental perplexities. However, in the FME technique, the weight of evaluating indicators is determined by the monitoring data compared to groundwater quality standard. As a result, when an abnormal value appears at some evaluating indicator, the condition of overestimating the weight of these indicators would lead to unrealistic evaluation results which may not be in line with the actual situation of the studied area (Zou et al. 2006).

Conclusions

Groundwater pollution is a vague concept because there are often no clear-cut boundaries that separate a “polluted” from an “unpolluted” sample. It is, therefore, necessary to develop a new method based on a fuzzy technique to give solutions that are robust and have a high level of confidence.

In this study, six groundwater samples were collected, analyzed and assessed for drinking water quality in the Quaternary Unconsolidated Sedimentary Basin near the Pi river. The pH value of the groundwater was slightly alkaline for most of the groundwater samples to basic in nature. The groundwater is classified as very hard and fresh water based on TH and TDS, respectively. Groundwater quality parameters were compared with the acceptable limits recommended by the national quality standards for groundwater of China (GB/T 14848-93). From all groundwater parameters analyzed, NH4, Fe, and Mn were above the permissible limits of (GB/T 14848-93). The sequence of the abundance of major ions is found in the order of Ca2+ > Mg2+ > Na+ > K+ and anions is \({\text{HCO}}_{3}^{ - }\) > \({\text{SO}}_{4}^{2 - }\) > Cl−.

The FME technique results show that five of the sampled groundwater (S1, S3, S4, S5, and S6) are suitable of drinking water directly while the well (S2) is unsuitable for drinking unless treated. The common contaminants in these samples are NH4, Fe, and Mn, which are mainly from the natural environment, industrial and agricultural activities. Thus, authorities should give more attention to the pollution of NH4, Fe, and Mn to prevent deterioration of good water quality by taking some effective measures that are required to enhance the drinking water quality by delineating an effective water quality management plan. This method may play an important role in decision-making for the drinking water quality assessment because it proved effective in solving problems of fuzzy boundaries. So, it is more objective and scientific and reliable in practice.

The FME method was compared with CEM in this study. Based on the results of the assessment obtained from both methods, the holistic picture of groundwater quality within the study area was satisfactory and consistent with the actual situation of the study area under the prevailing conditions. However, the fuzzy indicator is recommended as a more practical indicator for assessing groundwater quality owing to the introduction of membership degree and weight of each factor to the models.

The study can provide an important frame of reference to the government decision-making on improving groundwater quality in the study area. Additionally, this study may serve as a guide for future researchers to assess the groundwater conditions accurately and precisely, specifically for the North Chengdu Plain, China.

The degree of groundwater pollution risk has a direct connection to the water discharge and environmental vulnerability of the region. To improve the status of groundwater and thoughtful scientific planning of groundwater extraction, it is necessary to strictly control the industrial wastewater and domestic sewage discharge not only in the North Chengdu Plain but also in other watersheds.