Abstract
The adsorption of Cr(VI), Ni(II), Cd(II) and Pb(II), ions from aqueous solutions by Cucumis melo peel-activated carbon was investigated under laboratory conditions to assess its potential in removing metal ions. The adsorption behavior of metal ions onto CMAC was analyzed with Elovich, intra-particle diffusion rate equations and pseudo-first-order model. The rate constant of Elovich and intra-particle diffusion on CMAC increased in the sequence of Cr(VI) > Ni(II) > Cd(II) > Pb(II). According to the regression coefficients, it was observed that the kinetic adsorption data can fit better by the pseudo-first-order model compared to the second-order Lagergren’s model with R2 > 0.957. The maximum adsorption of metal ions onto the CMAC was found to be 97.95% for Chromium(VI), 98.78% for Ni(II), 98.55% for Pb(II) and 97.96% for Cd(II) at CMAC dose of 250 mg. The adsorption capacities followed the sequence Ni(II) ≈ Pb(II) > Cr(VI) ≈ Cd(II) and Ni(II) > Pb(II) > Cd(II) > Cr(VI). The optimum adsorption conditions selected were adsorbent dosage of 250 mg, pH of 3.0 for Cr(VI) and 6.0 for Ni(II), Cd(II) and Pb(II), adsorption concentration of 250 mg/L and contact time of 180.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Heavy metal ions such as Cr(VI), Ni(II), Zn(II), Cd(II) and Pb(II) are among the toxic inorganic pollutants that may cause environmental problem, although at low concentration in surface or subsurface water (Gupta and Nayak 2012; Gupta and saleh 2013; Gupta et al. 2013, 2015; Jain et al. 2003; Vinod et al. 2012; Saleh and Gupta 2012a). The conventional method for removing these toxic metal ions from aqueous solution is by chemical precipitation and the major drawback of this method is the generation of huge amount of chemical sludge (Gupta et al. 1997, 2011a, b, 2012; Mohammadi et al. 2011; Ahmaruzzaman and Gupta 2011). Adsorption is a simple treatment method for removing metal ions in wastewater, and activated carbon is a powerful adsorbent that is commonly used in industrial wastewater treatment plant (Saleh and Gupta 2011; Saleh and Gupta 2012a, b; Karthikeyan et al. 2012; Mittal et al. 2009a, b, 2010, 2012; Wang et al. 2006, 2009). The growing interest in this material is motivated by its favorable surface properties, uniformity of adsorption, and consequently exceptional adsorption effect (Zuorro and Roberto 2010; Saleh and Gupta 2012b; Saleh and Gupta 2014a, b; Li et al. 2016; Devaraj et al. 2016). A wide variety of materials have been investigated for this purpose and they can be classified into three categories: (1) natural materials, (2) agricultural wastes, (3) industrial wastes (Saravanan et al. 2013a, b, c, d, e, f, 2014a, b, c, 2015a, b, c, d; Rajendran et al. 2016; Huang et al. 2015). These materials are generally available at free of cost (Pollard et al. 1992). Various naturally occurring materials having characteristics of an adsorbent are available in large quantities. The abundance of these materials are used in many continents of the world and their low cost make them suitable as adsorbents for the removal of various heavy metals from waste waters such as chitosan, peat, wood, natural coal, bentonite, sawdust, chitin, radish leaves and Ricinus communis (Santhi and Manonmani 2009; Hadi Khani et al. 2010).
Thus, the present research aims to develop inexpensive and effective adsorbents using Cucumis melo peel a common agricultural waste, as an alternative to the existing commercial adsorbents. In addition, the present work is aimed to analyze the role of the surface chemistry in creating the activated carbon surface–metallic species interactions that govern the adsorption of Pb(II), Cd(II) and Ni(II) heavy metal ions. The adsorption behavior of heavy metals on CMAC was analyzed with Elovich, intraparticle diffusion model, Lagergren first-order model.
Materials and methods
Adsorbent
Preparation
Cucumis melo peel was collected from in and around pazhamudir nilayam of Coimbatore. The collected peels were cut into small pieces, washed with tap water several times to remove dust and dirt and rinsed with deionised distilled water and then dried. Cucumis melo peels were placed in the muffle furnace and carbonization was carried out at 200 °C for 2 h. The activated carbon thus obtained (here after CMAC) was ground well, sieved and the adsorbent of the size 75–125 μm has been used for the present study.
Experimental procedure
The adsorption experiment were performed in a batch mode in a series of beakers equipped with mechanical shaker by agitating 250 mg of the chosen adsorbent with 50 mL of metal ion solution with known previously determined, initial concentration of the considered heavy metal ion and the required initial pH value. The suspension was filtered and the remaining concentration of metal in the aqueous phase was determined. The final pH value was also measured. Batch adsorption experiment were performed by contacting 250 mg of the selected activated samples with 100 mL of the aqueous solution of different initial concentrations (100, 200, 300, 400 mg/L) of natural solution pH. The experiment were performed in a mechanical shaker at controlled temperature (25 + 2 °C) for a known period of time ranging between 10 and 210 min. At the end of the predetermined time, the suspension was filtered; the remaining concentration of Pb(II) in each sample after adsorption at different time intervals was determined by spectrophotometer after filtering the adsorbent with Whatman filter paper to make it carbon free. The batch process was used so that there is no need for volume correction. The Pb(II) concentration retained in the adsorbent phase was calculated according to
where Ci and Ce are the initial and equilibrium concentration (mg/L) of Pb(II) solution, respectively. V is the volume and W is the weight (g) of the adsorbent.
Results and discussion
Adsorption kinetics
The study of adsorption kinetics describes the solute uptake rate, and evidently this rate controls the residence time of the adsorbate uptake at the solid–solution interface, including the diffusion process. The mechanism of adsorption depends on the physical and chemical characteristics of the adsorbents as well as on the mass transfer process. The results obtained from the experiments were used to study the kinetics of the metal ion adsorption. The rate kinetics of the metal ion adsorption on the CMAC was analyzed, using the pseudo-first-order (Lagergren 1898), Elovich and intraparticle diffusion (Weber and Morris 1963) models. The conformity between the experimental data and the model predicted values was expressed by the correlation coefficient (R2).
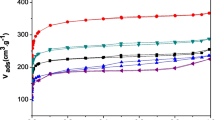
Figure 1a–d displays the kinetic curves related to adsorption of Cr(VI), Pb(II), Ni(II) and Cd(II) on Cucumis melo peel-activated carbon. Equilibrium contact times from kinetic curves of heavy metals were determined. The optimum agitation time was fixed as 180 for all metal ions. These findings suggest that adsorption kinetic curves of heavy metals fitted the kinetic curve of the first degree.
The greater adsorption rate constant shows that adsorbates are adsorbed faster by the adsorbent.
According to adsorption rate constants, the heavy metal ions used are changing in the order of Ni2+ > Pb2+ > Cd2+ > Cr2+. This order was confirmed by equilibrium contact times determined from their kinetic curves.
Adsorption rate constants (Ka) were determined using these curves.
Lagergren rate equation
The Lagergren rate constant for the adsorption of the Cr(VI), Cd(II), Pb(II) and Ni(II) metal ions from aqueous solution and from industrial effluent on the adsorbent CMAC is determined using Lagergren equation (Bhatnagar and Minocha 2006):
where q is the amount of metal adsorbed (mg/g) by the adsorbent at time ‘t’, qe is the amount of metal adsorbed (mg/g) by the adsorbent at equilibrium time, Ka is the rate constant of adsorption in time−1 and t is the agitation time in minutes.
Experimental data for adsorption capacity of Cr6+, Pb2+, Ni2+ and Cd2+ from aqueous solution by activated carbon (Tables 1, 2, 3, 4).
The model has been widely used by researchers on kinetic study of metal ions adsorption onto various derived adsorbents (Rengaraj et al. 2003, 2004; Li et al. 2011; Argun and Dursun 2008). Batch mode experiments were carried out by varying the concentration of the metal solutions at 27 °C and at pH 3.0 for Cr(VI) metal ion and at pH 6.0 for Cd(II), Pb(II) and Ni(II) metal ions used in this study. The data obtained from Lagergren equation for the adsorption of the metals in terms of initial concentration of the metal solutions with the adsorbent CMAC. The linear plot obtained shows the applicability of Lagergren rate equation for the adsorption of the metal ions used in this study and suggested the formation of monolayer of metal ions onto the surface of the adsorbent (Madhava Rao et al. 2009). The rate constants Ka are calculated from the slope of the plots of log(qe − q) vs t. The values of correlation coefficient (r2) obtained show good correlation. The reason for this behaviour can be attributed to the high competition for the adsorption surface sites at high concentration which leads to lower adsorption rates (Venkata Subbaiah et al. 2009). From the slope of each line, the rate constants were determined. Figure 2 shows the linear plots of log(qe − q t ) against t. Table 5 shows the amount of adsorption equilibrium (qe), Lagergren’s rate constant (Kad) and the correlation coefficient (R2) which are derived from the Lagergren’s equation.
As shown in Table 5, the values of R2 for the metal ion adsorption onto activated sludge are larger than 0.85 and higher compared to the adsorption of the metal ions onto dried sludge. This shows that the adsorption of Cr(VI), Ni(II), Pb(II) and Cd(II) onto CMAC was well fitted with the first-order Lagergren’s model.
Intraparticle diffusion rate equation
There is a possibility of transport of metal ion molecules from the bulk into pores of the adsorbent as well as adsorption at the outer surface of the adsorbent. The rate-limiting step in the adsorption may be either film diffusion or intraparticle diffusion. As they act in series, the slower of the two will be the rate-determining step. The possibility of the metal ion species to diffuse into the interior sites of the particles of adsorbent was tested with Weber–Morris equation given as follows (Lalitha et al. 2009):
where ‘q’ is the amount of metal adsorbed (mg/g) by the adsorbent at time ‘t’, Kp is the intraparticle diffusion rate constant and ‘t’ is the time (agitation time) in minutes.
To study the diffusion process, batch mode experiments are carried out with the adsorbent CMAC at 27 °C and at pH 3 for Cr(VI) and at pH 6 for Pb(II), Cd(II) and Ni(II) by varying the initial concentration of the metal solutions used in this study.
The rate constant for intraparticle diffusion Kp for initial concentrations of the metal ion is determined from the slope of the linear equation drawn between square root of time (t1/2) and the amount of adsorbate adsorbed (q).
If the intraparticle diffusion is the rate-controlling step, the plot should be linear and pass through the origin. It can be noticed from Fig. 2, the plots are linear but not passing through the origin and this deviation from the origin or near saturation might be due to the difference in mass transfer rate in the initial and final stages of adsorption (Renugadevi et al. 2011). It also indicates that there is an initial boundary layer resistance and intraparticle diffusion is not the sole rate-controlling step, but other kinetic models may simultaneously control the adsorption rate (Anoopkrishnan et al. 2011).
Table 6 shows intraparticle diffusion rate constant (Kad) and the correlation coefficient (R2) which are derived from the intraparticle diffusion rate equation. As shown in Fig. 3, the plot of intra-particle diffusion model given a straight line to the data obtained with R2 greater than 0.9. This shows the adsorption of Cr(VI), Pb(II), Ni(II) and Cd(II) ions onto the CMAC was through the intra-particle diffusion process.
Elovich rate equation
The Elovich equation was developed to describe the kinetics of chemisorption of gases onto solids and it is generally expressed as:
where ‘q t ’ is the amount of metal adsorbed (mg/g) by the adsorbent at time ‘t’, ‘α’ is the initial adsorption rate (mg/g min) and ‘β’ is the desorption constant (g/mg) during any experiment.
Assuming the initial boundary condition, q = 0 at t = 0, the above equation on integration become:
To simplify the Elovich’s equation, Chien and Clayton (1980) assumed αβ ≫ 1 and applying the boundary conditions qt = 0 at t = 0 and qt = qt at t = t, equation becomes (Patil et al. 2011):
This equation is commonly used for the chemisorptions, which is probably the mechanism that controls the rate of adsorption. This model can be applied with success in liquid solution (Khaoya and Pancharoe 2012). Figure 4 shows the Elovich plots of ln t vs q (amount of metal adsorbed (mg/g) by the adsorbent at time ‘t’). It gives a linear relationship with a slope of 1/β and an intercept of 1/β ln(αβ). The Elovich equation data obtained in this study for the adsorption of Cr(VI), Pb(II), Cd(II) and Ni(II) from aqueous solution onto CMAC. The high correlation coefficient (r2) shows the successfulness of the Elovich model.
Table 7 shows desorption constant (β), initial adsorption rate constant (α) and the correlation coefficient (R2) which are derived from the Elovich rate equation.
The higher value of initial adsorption rate (α) may be due to the greater surface area of the adsorbent CMAC, for the immediate adsorption of metal ions from aqueous solution and also from industrial effluent. The decrease in the value of desorption constant (β) with the increase of the initial concentration of the metal solutions (Patil et al. 2011).
Conclusion
The adsorption behavior of Cr(VI), Pb(II), Ni(II) and Cd(II) ions onto the Cucumis melo peel-activated carbon was analyzed with Elovich rate equation, intra-particle diffusion model and Lagergren’s first-order model. The kinetic adsorption data can fit better by the pseudo-first-order Lagergren’s model and Elovich’s rate equation indicating the rate-limiting step in the adsorption of Cr(VI), Pb(II), Ni(II) and Cd(II) ions could be ascribed to the chemical interaction between the metal ions and the functional groups at the surface of activated carbon. The Elovich’s equation data obtained in this study for the adsorption of Cr(VI), Pb(II), Cd(II) and Ni(II) from aqueous solution onto CMAC. The high correlation coefficient (r2) shows the successfulness of the Elovich’s model.
References
Ahmaruzzaman M, Gupta VK (2011) Rice husk and its ash as low-cost adsorbents in water and wastewater treatment. Ind Eng Chem Res 50(24):13589–13613
Anoopkrishnan K, Sreejalekshmi KG, Baiju RS (2011) Nickel(II) adsorption onto biomass based activated carbon obtained from sugarcane bagasse pith. Bioresour Technol 102:10239–10247
Argun E, Dursun S (2008) A new approach to modification of natural adsorbent for heavy metal adsorption. Bioresour Technol 99(7):2516–2527
Bhatnagar A, Minocha A (2006) Conventional and non-conventional adsorbents for removal of pollutants from water—a review. Indian J Chem Technol 13:203–217
Chien SH, Clayton WR (1980) Application of elovich equation to the kinetics of phosphate release and sorption in soils. J Soil Sci Soc Am 44:265–268
Devaraj M, Saravanan R, Deivasigamani R, Gupta VK, Gracia F, Jayadevan S (2016) Fabrication of novel shape Cu and Cu/Cu2O nanoparticles modified electrode for the determination of dopamine and paracetamol. J Mol Liq 221:930–941
Gupt VK, Jain R, Mittal A, Saleh TA, Nayak A, Agarwal S, Sikarwar S (2012) Photo-catalytic degradation of toxic dye amaranth on TiO2/UV in aqueous suspensions. Mater Sci Eng 32(1):12–17
Gupta VK, Nayak A (2012) Cadmium removal and recovery from aqueous solutions by novel adsorbents prepared from orange peel and Fe2O3 nanoparticles. Chem Eng J 180:81–90
Gupta VK, Saleh TA (2013) Sorption of pollutants by porous carbon, carbon nanotubes and fullerene—an overview. Environ Sci Pollut Res 20:2828–2843
Gupta VK, Srivastava SK, Mohan D (1997) Design parameters for fixed bed reactors of activated carbon developed from fertilizer waste for the removal of some heavy metal ions. Waste Manag 17(8):517–522
Gupta VK, Agarwal S, Saleh TA (2011a) Synthesis and characterization of alumina-coated carbon nanotubes and their application for lead removal. J Hazard Mater 185:17–23
Gupta VK, Jain R, Nayak A, Agarwal S, Shrivastava M (2011b) Removal of the hazardous dye—tartrazine by photodegradation on titanium dioxide surface. Mater Sci Eng C 31(5):1062–1067
Gupta VK, Ali I, Saleh TA, Nayak A, Agarwal S (2012) Chemical treatment technologies for wastewater recycling—a review. RSC Adv 2:6380–6388
Gupta VK, Kumar R, Nayak A, Saleh TA, Barakat MA (2013) Adsorptive removal of dyes from aqueous solution onto carbon nanotubes: a review. Adv Colloid Interface Sci 193–194:24–34
Gupta VK, Nayak A, Agarwal S (2015) Bioadsorbents for remediation of heavy metals: current status and their future prospects. Environ Eng Res 20(1):001–018
Huang YQ, Yang CP, Sun ZC, Zeng GM, He HJ (2015) Removal of cadmium and lead from aqueous solutions using nitrilotriacetic acid anhydride modified ligno-cellulosic material. RSC Adv 5(15):11475–11484
Jain AK, Gupta VK, Bhatnagar A, Suhas (2003) A comparative study of adsorbents prepared from industrial wastes for the removal of dyes. Sep Sci Technol 38(2):463–481 (Impact factor −1.028)
Karthikeyan S, Gupta VK, Boopathy R, Titus A, Sekaran G (2012) A new approach for the degradation of high concentration of aromatic amine by heterocatalytic Fenton oxidation: kinetic and spectroscopic studies. J Mol Liq 173:153–163
Khani H, Rofouei MK, Arab P, Gupta VK, Vafaei Z (2010) Multi-walled carbon nanotubes-ionic liquid-carbon paste electrode as a super selectivity sensor: application to potentiometric monitoring of mercury ion(II). J Hazard Mater 183(1–3):402–409
Khaoya S, Pancharoe U (2012) Removal of lead(II) from battery industry wastewater by HFSLM 98. Int J Chem Eng Appl 3:2
Lagergren S (1898) About the theory of so-called adsorption of soluble substances. Kungliga Srenska Vetenskapsakademiens Handlingar 24:1–39
Lalitha P, Rajalakshmi R, Subhashini S (2009) Usefulness of activated carbon prepared from industrial wastes in the removal of Nickel from aqueous solution. E J Chem 6(2):361–370
Li X, Li Y, Ye Z (2011) Preparation of macroporous bead adsorbents based on poly(vinyl alcohol)/chitosan and their adsorption properties for heavy metals from aqueous solution. Chem Eng J 178(15):60–68
Li X, Yu J, Jaroniec M (2016) Hierarchical photocatalysts. Chem Soc Rev 45:2603–2636
Madhava Rao M, Ramana DK, Seshaiah K, Wang MC, Chang Chien SW (2009) Removal of some metal ions by activated carbon prepared from Phaseolus aureus hulls. J Hazard Mater 166:1006–1013
Mittal A, Kaur D, Malviya A, Mittal J, Gupta VK (2009a) Adsorption studies on the removal of coloring agent phenol red from wastewater using waste material as adsorbents. J Colloid Interface Sci 337:345–354
Mittal A, Mittal J, Malviya A, Gupta VK (2009b) Adsorptive removal of hazardous anionic dye Congo red from waste water using waste materials and recovery by desorption. J Colloid Interface Sci 340:16–26
Mittal A, Mittal J, Malviya A, Kaur D, Gupta VK (2010) Decoloration treatment of a hazardous triarylmethane dye, Light Green SF (Yellowish) by waste material adsorbents. J Colloid Interface Sci 342(2):518–527
Mittal A, Jhare D, Mittal J, Gupta VK (2012) Batch and bulk removal of hazardous colouring agent rose bengal by adsorption over bottom ash. RSC Adv 2(22):8381–8389. https://doi.org/10.1039/C2RA21351F
Mohammadi N, Khani H, Gupta VK, Amereh E, Agarwal S (2011) Adsorption process of methyl orange dye onto mesoporous carbon material—kinetic and thermodynamic studies. J Colloid Interface Sci 362:457–462
Patil S, Renukdas S, Patel N (2011) Removal of methylene blue, a basic dye from aqueous solutions by adsorption using teak tree (Tectona grandis) bark powder. Int J Environ Sci 1(5):711–725
Pollard SJT, Fowler GD, Sollars CJ, Perry R (1992) Low-cost adsorbents for waste and waste water treatment—a review. Sci Total Environ 116:31–52
Rajendran S, Khan MM, Gracia F, Qin J, Gupta VK, Arumainathan S (2016) Ce3+-ion-induced visible-light photocatalytic degradation and electrochemical activity of ZnO/CeO2 nanocomposite. Sci Rep 6:31641
Rengaraj S, Joo CY, Kim Y, Yi J (2003) Kinetics of removal of chromium from water and electronic process wastewater by ion exchange resins: 1200H, 1500H and IRN97H. J Hazard Mater 102(2–3):257–275
Rengaraj S, Kim Y, Joo CK, Yi J (2004) Removal of copper from aqueous solution by aminated and protonated mesoporous aluminas: kinetics and equilibrium. J Colloid Interface Sci 73(1):14–21
Renugadevi N, Anitha G, Lalitha P (2011) Hexavalent chromium removal using a low-cost activated carbon adsorbent from Areca catechu. Indian J Environ Prot 31(1):52–58
Saleh TA, Gupta VK (2011) Functionalization of tungsten oxide into MWCNT and its application for sunlight-induced degradation of rhodamine B. J Colloid Interface Sci 362(2):337–344
Saleh TA, Gupta VK (2012a) Column with CNT/magnesium oxide composite for lead(II) removal from water. Environ Sci Pollut Res 19(4):1224–1228
Saleh TA, Gupta VK (2012b) Photo-catalyzed degradation of hazardous dye methyl orange by use of a composite catalyst consisting of multi-walled carbon nanotubes and titanium dioxide. J Colloid Interface Sci 371(1):101–106
Saleh TA, Gupta VK (2014a) Processing methods: characteristics and adsorption behavior of tire derived carbons: a review. Adv Colloid Interface Sci 211:92–100
Saleh TA, Gupta VK (2014b) Processing methods, characterization and adsorption behavior of tire derived carbons: a review. Adv Colloid Interface Sci 211:93–101
Santhi T, Manonmani S (2009) Uptake of cationic dyes from aqueous solution by bioadsorption using granulized Annonasqumosa. E J Chem 6(4):1260–1266
Saravanan R, Karthikeyan S, Gupta VK, Sekaran G, Narayanan V (2013a) Enhanced photocatalytic activity of ZnO/CuO nanocomposite for the degradation of textile dye on visible light illumination. Mater Sci Eng C 33(1):91–98
Saravanan R, Gupta VK, Prakash T, Narayanan V, Stephen A (2013b) Synthesis, characterization and photocatalytic activity of novel Hg doped ZnO nanorods prepared by thermal decomposition method. J Mol Liq 178:88–93
Saravanan R, Thirumal E, Gupta VK, Narayanan V, Stephen A (2013c) The photocatalytic activity of ZnO prepared by simple thermal decomposition method at various temperatures. J Mol Liq 177:394–401
Saravanan R, Joicy S, Gupta VK, Narayanan V, Stephen A (2013d) Visible light induced degradation of methylene blue using CeO2/V2O5 and CeO2/CuO catalysts. Mater Sci Eng C 33(8):4725–4731
Saravanan R, Gupta VK, Narayanan V, Stephen A (2013e) Comparative study on photocatalytic activity of ZnO prepared by different methods. J Mol Liq 181:133–141
Saravanan R, Karthikeyan N, Gupta VK, Thirumal E, Thangadurai P (2013f) ZnO/Ag nanocomposite: an efficient catalyst for degradation studies of textile effluents under visible light. Mater Sci Eng C 33(4):2235–2244
Saravanan R, Gupta VK, Mosquera E, Gracia F (2014a) Preparation and characterization of V2O5/ZnO nanocomposite system for photocatalytic application. J Mol Liq 198:409–412
Saravanan R, Prakash T, Gupta VK, Stephen A (2014b) Tailoring the electrical and dielectric properties of ZnO nano rods by substitution. J Mol Liq 193:160–165
Saravanan R, Gupta VK, Narayanan V, Stephen A (2014c) Visible light degradation of textile effluent using novel catalyst ZnO/γ-Mn2O3. J Taiwan Inst Chem Eng 45(4):1910–1917
Saravanan R, Gupta VK, Mosquera E, Gracia F, Narayanan V, Stephen A (2015a) Visible light induced degradation of methyl orange using β-Ag 0.333 V2O5 nanorod catalysts by facile thermal decomposition method. J Saudi Chem Soc 19(5):521–527
Saravanan R, Gracia F, Khan MM, Poornima V, Gupta VK, Narayanan V (2015b) ZnO/CdO nanocomposites for textile effluent degradation and electrochemical detection. J Mol Liq 209:374–380
Saravanan R, Khan MM, Gupta VK, Mosquera E, Gracia F et al (2015c) ZnO/Ag/CdO nanocomposite for visible light-induced photocatalytic degradation of industrial textile effluents. J Colloid Interface Sci 452:126–133
Saravanan R, Khan MM, Gupta VK, Mosquera E et al (2015d) ZnO/Ag/Mn2O3 nanocomposite for visible light-induced industrial textile effluent degradation, uric acid and ascorbic acid sensing and antimicrobial activity. RSC Adv 5:34645–34651
Venkata Subbaiah M, Vijaya Y, Sivakumar N, Subba Reddy A, Krishnaiah A (2009) Biosorption of nickel from aqueous solutions by Acacia leucocephala bark: kinetic and equilibrium studies. Colloids Surf B 74:260–265
Vinod KN, Mary ER, Gunaseeli R, Kannan ND, Sridhar J (2012) Modelling and structural analysis of cellulases using clostridium thermocellum as template. Bioinformation 8(22):1105–1110
Wang JL, Chen C (2006) Biosorption of heavy metals by Saccharomyces cerevisiae: a review. Biotechnol Adv 24:427–451
Wang JL, Chen C (2009) Biosorbents for heavy metals removal and their future. Biotechnol Adv 27:195–226
Weber WJ, Morris JC (1963) Kinetics of adsorption on carbon from solution. J Sanit Eng Div Am Soc Civ Eng 89:31–60
Zuorro A, Roberto L (2010) Adsorption of Pb(II) on spent leaves of green and black tea. Am J Appl Sci 7:153–159
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Manjuladevi, M., Anitha, R. & Manonmani, S. Kinetic study on adsorption of Cr(VI), Ni(II), Cd(II) and Pb(II) ions from aqueous solutions using activated carbon prepared from Cucumis melo peel. Appl Water Sci 8, 36 (2018). https://doi.org/10.1007/s13201-018-0674-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-018-0674-1