Introduction

A water distribution network (WDN) is a network of interconnected pipes involving several components. Each network is unique in source, layout, topography of service area, pipe material, valves and meters and consumer connections. Hydraulic simulation model are widely used for predicting the behavior of the network in terms of nodal heads and pipe discharges. However, disagreement between model-simulated behavior and actual field behavior often exists because of uncertainty in input parameters used in the model. Before any intended use of the WDN model, it must be ensured that the model would predict, with reasonable accuracy, the behavior of the network in real time. The process of adjusting the value of uncertain parameters in the network modeling to match values of modeled parameters with those observed in the field is called calibration of the model (Walski 1983a; Ormsbee and Wood 1986; Bhave 1988). Walski (1983b) precisely defined calibration as “a two step process consisting of: (1) comparison of pressures and flows predicted with observed pressures and flows for known operating conditions (i.e., pump operation, tank levels, pressure reducing valve (PRV) settings); and (2) adjustment of the input data for the model to improve agreement between observed and predicted values.”

Calibration is a challenging task, as a large numbers of input parameters are involved (e.g., nodal elevations and demands including water losses; pipe length, diameter and roughness coefficients; the rate of water supply and water level at the source; pump characteristics; valve settings, etc.) and depends on the accuracy of these parameters gathering and preparation. Therefore, it is desirable that some of these parameters are measured accurately during field observations so that there are few uncertain parameters requiring adjustments. Further, instead of developing different flow conditions to get the flow and pressure readings, a computerized flow and pressure measurement with a data logger provides fairly accurate flow and pressure at various operating conditions in a day. Field observations and measurements provide reliable data regarding pipe length and material, ground elevations, operational settings and status of valve and water supply and level at the source node. The nodal demands are obtained from the consumer usage information, i.e., from billing data, and non-revenue water (NRW) is adjusted. The corrosion and deposition processes over a time after the pipe has been installed make difficult to determine actual pipe diameter. Therefore, normal pipe diameter obtained during field observation is used in the hydraulic model and the roughness coefficient is adjusted to compensate for the change in the diameter. In general, therefore data regarding the pipe length, diameter and material, nodal elevation and demands adjusting NRW and water level and supplies at the source node obtained during field observations are considered fairly reliable and do not need any adjustment during calibration. However, the pipe roughness coefficients are less reliable and therefore may need adjustment during calibration.

Several methods have been suggested to simultaneously adjust pipe roughness coefficients and nodal demands (Bhave and Gupta 2006), or pipe roughness coefficient only with the assumption that nodal demands are fairly accurate and do not need any adjustment. The calibration of the model could be carried out through explicit approaches (e.g., Ormsbee and Wood 1986; Bhave 1988; Boulos and Wood 1990; Todini 1999) in which unknown pipe roughness coefficients are obtained by framing hydraulic equations using the observed flow and pressure values. The same number of equations are required as the number of unknowns. The other types of methods for calibration of the model are implicit approaches (e.g., Ormsbee 1989; Lansey and Basnet 1991; Datta and Sridharan 1994; Greco and Giudice 1999; Greco and Di Cristo 1999; Lansey et al. 2001; Kapelan 2002; Lingireddy and Ormsbee 2002; Bascià and Tucciarelli 2003; Kapelan et al. 2007; Koppel and Vassiljev 2009; Alvisi and Franchini 2010), in which field-observed and measured parameters are treated as known parameters and directly used in the model analysis. The implicit approach requires that the number of flow and pressure measurements exceed the number of unknowns. The implicit problem formulation can be solved using optimization techniques [e.g., nonlinear programming (NLP) or evolutionary technique like GA].

Reasonable agreement of the model is usually judged in terms of the differences in the observed and predicted pressures or heads at the test nodes (e.g., Cesario and Davis 1984; Eggener and Polkowski 1976; Rahal et al. 1980; Walski 1983b), and depends on the accuracy of the data set and the effort and cost the model user is prepared to spend in fine-tuning the model. Walski (1983b) states that an average difference of ± 1.5 m with a maximum value of ± 5.0 m for a good data set and the corresponding values of ± 3.0 m and ± 10 m for a poor data set would be a reasonable target. Cesario and Davis (1984) state that the model can be calibrated to an accuracy of 3.5–7 m.

Instead of judging the calibration through only differences and/or ratios of the observed to the predicted pressure or head loss differences between the test nodes and nearby boundary locations (reservoirs/tanks) having known pressures or heads (Walski 1986), it is preferable to judge the calibration through minimizing the summation of the sum of square of difference between the measured and simulated value of pressure heads at test nodes as done in most of the implicit approaches The Research Committee on Water Distribution Systems of the American Water Works Association (1974) states that “the major source of error in simulation of contemporary performance will be in the assumed loadings distribution and their variations”. On the other hand, Eggener and Polkowski (1976) state that the weakest piece of input information is not the assumed loading condition, but the pipe friction factor. From these conflicting views, it is clear that, in some cases, the adjustment in the pipe head-loss coefficients may be more predominant than the adjustment in the nodal consumptions, while the opposite may be the situation in other cases (Shamir and Howard 1977). Walski (1986) suggested consideration of multiple demand loadings for reliable model calibration, which can be generated through pump on/off conditions or excessive withdrawal at one or few nodes by opening fire hydrants. The novelty of the study herein is the use of online data of flow and pressures that provided a set of observations under various loadings. This paper demonstrates that with the online pressure and flow data at few observational points in the network, it is possible to accurately calibrate a model of a real WDN by adjusting the pipe roughness coefficients only. This is achieved by providing accurate inputs about pipe lengths, diameters and materials, nodal elevations, nodal demands, valve status and its opening. The importance of the valve is recognized, as these are used for isolation as well as pressure and flow control purpose by throttling. The usual way of considering head loss through them as minor loss and clubbing their effects in adjusting pipe roughness coefficient results in a very absurd value of pipe roughness coefficients.

Water distribution network details

Nagpur, a second capital of Maharashtra State, is situated in the center of India. The population of the city is 2.53 million (2015), spread over 217 sq. km. The total water supply to the city is over 670 MLD through 67 service reservoirs and 3200 km-long distribution network covering 239 thousands connections. The WDN under consideration consists of one hydraulic zone of Ramnagar GSR located at the western part of Nagpur City and composed of residential areas with all types of dwellings including slum as well as commercial areas. During conversion of mode from intermittent to continuous in the year 2007, all property connections were changed, faulty meters were replaced/repaired, illegal connections were removed/regularized, public stand posts were converted to grouped pipe connections with metering, and old pipelines (about one-third of total pipelines) were replaced by new pipelines.

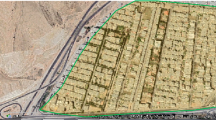
The WDN under consideration as shown in Fig. 1 consists of 292 nodes and 375 pipes. Valves are considered as separate entity to include proper head loss through them during calibration. Therefore, while considering the valve locations as given later in Table 2, some of the pipes got split into two pipes. In the model considered herein, the number of pipes has increased to 434. Out of 292 nodes, 234 are non-zero demand nodes. The network is divided into 20 subzones to control pressure and flow through the 59 valves. Flow and pressure in each of the subzone is controlled by one or more valves.

Fig. 1
figure 1

Ramnagar GSR operational water distribution network

Full size image

Data collection and preparation

Data collection and preparation include: (1) network skeletonization; (2) source heads and supply at source nodes; (3) nodal demands; (4) pipe and valve details.

Network skeletonization

Service connections of small-diameter pipes were removed. Thus, the network consisted of all pipes up from source to the individual property, the diameter of which are varying from 80 to 450 mm. Further, demands were lumped and assumed to be concentrated at nodes. Coverage and boundary of the network were verified and the zero pressure test was carried out. The valve positions were located correctly and operational settings were verified to obtain more realistic values of pipe roughness coefficients.

Source head and supply from source

The storage facility is modeled as reservoir R1 having a capacity of 0.91 ML and elevation is determined accurately from the available records and verified by field survey. The elevation of GSR is 327.205 m. The storage facility is connected to an automated device to measure and record the depth of water in the reservoir at any time. The supervisory control and data acquisition (SCADA) is used to acquire water level variation information of the reservoir based on the head at the reservoir H st , and HGL multiplier at time t was created as shown in Table 1. The hourly water supply rate Q st from reservoir R1 is measured with a reasonable degree of accuracy for 24 h by installing a digital water flow meter (FM) with data logger at outflow pipe.

Table 1 Flow from GSR and observation of the level in the tank and pressures at selected observation points on 08.11.2014
Full size table

Nodal demands

The nodal demands are obtained from the consumer usage information, i.e., from billing data. The billing data covers the water usage of 2816 consumers billed quarterly, and 632 consumers billed monthly. The consumer data includes consumer index number, meter number, meter installation date, consumer address and meter reading with date. The average daily water demand of the entire WDN q d is obtained based on the consumer data (2012) for three billing cycles of both types of consumers that are billed quarterly and monthly. Each house service connection (HSC) is geographically linked with pipe number using street addresses with plot number in the billing data and location of the consumer meter. The consumer demands are allocated mainly to downstream node of pipe. Wherever it was not easy to identify the downstream node, the demands were distributed to both the junctions by experience and judgment. The difference between the daily supply and the quantity of water billed to consumer per day is non-revenue water (NRW), q u .

According to the node flow continuity equation, the algebraic sum of the flows at a node must be zero. Thus,

$$ \sum\limits_{{(e\varepsilon {\text{ No}} . {\text{ of sources}})}} {({}_{e}Q_{s} } + q_{dj} + q_{uj} ) = 0\;\;\;\;{\text{for all nodes}}\;j, $$
(1)

where e Q s is the flow into the WDN from the source e, m3/s; q dj is the external flow such as water demand at the node j, L/s; and q uj is the external—unaccounted—flow (= NRW) at node j, L/s.

The generalized diurnal demand pattern for the entire distribution network is created based on an hourly flow recorded by the flow meter installed on the outlet pipe of the Ramnagar GSR, i.e., at inlet of the distribution network and applied to the all DMA/subzones. Individual diurnal demand pattern for each DMA/subzones could not be created due to lack of flow meter at the inlet of each DMA/subzone. The observation of flow from the source and water level in the reservoir on the day of observation (November 8, 2014) are given in Table 1. The average flow during the day was 504.44 m3/h. Flow multipliers as a ratio of hourly flow to average flow were obtained for extended period simulation as given in Table 1.

Pipe and valve details

The most difficult task in calibrating a WDN is the proper selection of the pipe roughness coefficients such as the Hazen–Williams coefficients. For estimation of pipe roughness coefficients, it is preferable to have a field survey regarding pipe materials and the year of installation. Pipes of different materials such as cast iron, ductile iron and HDPE have been installed at different locations and at different times. The length and diameter of all pipes are obtained from available records and validated by field survey. The initial Hazen–Williams (HW) coefficients are assigned groupwise on the basis of pipe material and age of installation in years as: Group 1 (CI above 30 years)—85; Group 2 (CI below 30 years)—100; Group 3 (DI below 10 years)—125; and Group 4 (HDPE below 10 years)—135. The numbers of pipe in the four groups 1–4 were 11, 216, 49 and 158, respectively.

The basic equation governing the head loss in WDN is the loop head-loss equation. According to the loop head-loss equation, the algebraic sum of the head losses in pipes of a loop must be zero. Thus,

$$ \sum\limits_{i\,\varepsilon \,c} {h_{Li} } = 0\;\; {\text{for all loop c}}, $$
(2)

where \( h_{Li} \) is the head loss in pipe i contained in loop c.The head loss in a pipe is generally expressed by the Hazen–Williams (HW) formula:

$$ h_{L} = \frac{{KLQ^{1.852} }}{{C^{1.852} D^{4.87} }}, $$
(3)

where K is the constant depending on the units of other terms in the HW formula; L is the length of the pipe in m; Q is the flow in pipe in L/s; C is the HW coefficient; D is the diameter of the pipe in millimeters.

In India and other developing countries, sluice valves provided for isolation are used to control flows by reducing pressures through throttling. The details of the valves regarding their locations, size, total number of threads and the number of threads open are very crucial. These were obtained from the field as in Table 2. The percentage closure of valve is obtained for each valve. For each closure, an independent pattern can be given. However, instead of an independent pattern, 14 patterns from fully open to fully closed valve conditions are considered based on the valve closure observed in the field to reduce the computation work without losing much accuracy (Table 2).

Table 2 List of the valves with operational status during the study
Full size table

The hydraulic model calibration process

In this calibration process, it is considered that the pipe length, diameter and material, nodal elevation, nodal demand (i.e., q d from billing data), flow and head measurement at the source are obtained/measured reasonably accurately. The model is calibrated by adjusting the NRW demand uniformly and the pipe roughness coefficients for the group of pipes by the same amount to minimize the summation of the sum of square of difference between the measured and simulated values of the pressure head at the observation points (Greco and Del Guidice 1999; Greco and Di Cristo 1999). Gupta and Bhave (2007) showed that the impact of change in pipe roughness on nodal pressures is monotonic. They further showed that monotonic behavior continues when the pipe roughness of the group of pipes is changed simultaneously. Thus, if the observed pressure at the node is more than the modeled pressure and the impact of increasing the roughness value for a particular group of pipe is to increase the pressure head at the observation node, then the pipe roughness value for that group of pipes needs to be increased, or otherwise. Iterative trial and error procedure is used to minimize the sum of square of errors. Alternatively, any suitable optimization approach based on NLP or GA can be used. The problem can be formulated as

$$ \hbox{min} Z = \sum\limits_{i = 1}^{n} {\sum\limits_{t = 0}^{T} {\left( {{}_{i}P_{t}^{m} - {}_{i}P_{t}^{s} } \right)} }^{2} , $$
(4)

where \( _{i} P_{t}^{m} \) is the measured pressure head at observation point i at time t; \( _{i} P_{t}^{s} \) is the model-predicted (simulated) pressure head at observation point i at time t.

The WDN is shown in Fig. 1, in which reservoir source is shown as R1 and three pressure monitoring points are shown as PMP-1, PMP-2, and PMP-3. The measured head Hst and flow Qst at the source node and pressure head at three pressure monitoring points at time t in a day are shown in Table 1 as \( _{1} P_{t}^{m} \), \( _{2} P_{t}^{m} \) and \( _{3} P_{t}^{m} \) at time t in a day as shown in Table 1. Based on the above flow data, the total inflow into the network is worked out as Q s  = 12.107 MLD and the average daily demand for the entire WDN is worked out as q d  = 7.097 MLD based on the billing data. Thus, the NRW, q u is 5.010 MLD and adjusted uniformly (q u /j n ) = 0. 1986 Lps to all nodes, irrespective of the demand at the nodes, so that the algebraic sum of the predicted nodal demands of the entire network equals the measured system inflow. Therefore, even if the demand at the node is zero, water losses are considered at that node. For better adjustment of the NRW demand, the network may be divided into several DMAs and NRW, and the hydraulic pattern for each DMA is worked out by installing a flow meter at the inlet of each DMA for better calibration. Hence, this calibration process assumed that the prepared data and predicted nodal demands were reasonably accurate and the model calibrated by adjusting only the pipe roughness coefficients for the group of pipes by the same amount to minimize the summation of the sum of square of difference between the measured and simulated values of the pressure heads (Eq. 4) at the observation points. With the correctly prepared input data and initially assumed pipe roughness coefficient values, the network is simulated, and the simulated pressure heads \( _{1} P_{t}^{s} \), \( _{2} P_{t}^{s} \) and \( _{3} P_{t}^{s} \) are noted at the observational points every hour in a day. The simulated pressure heads are compared with field-measured pressure heads at three predetermined pressure-monitoring points PMP-1, PMP-2 and PMP-3. The comparison showed that model-simulated pressure heads at all PMPs were greater and did not match with the field-measured pressure heads. This requires adjustment of C values. Valves location and setting are considered during calibration so that C values of pipes do not become unrealistic.

Now, to know the impact of changing C values on pressure heads at observation nodes, the C values of different groups of pipes were changed (herein reduced by 5), one by one, and the pressure head values on the observational nodes were noted as shown in Table 3. It can be observed that the pressure heads are reduced at the observational nodes in all cases by reducing the C values. The impact of changing the C value of pipes of Group 1 is very less and the pressure head values are same even up to the fifth place of decimal. Since the measured field pressure heads are less than the simulated pressure heads, the C values are required to be reduced to reduce the simulated pressure heads.

Table 3 Pressure heads at observation nodes on changing HW values for pipes in different groups one by one
Full size table

As the simulated pressure heads are higher than the measured pressure heads with initially assumed C values, the C values are reduced by the same value for all pipe groups and the network is simulated to obtain the least value of the summation of the sum of the square of difference between the measured and simulated pressure heads. Initially, with the assumed values of pipe roughness coefficients, the summation of the sum of square of difference between the measured and simulated pressure head values were obtained as 34.24 (row 1, Table 4). The pipe roughness values are then reduced by a unit and again the summation of the sum of square of difference between the measured and simulated pressure head values obtained. The minimum value of summation is 18.32 when the C values for Groups 1–4 are 79, 94, 119 and 129.

Table 4 Summation of sum of square of difference between the measured and simulated pressure heads
Full size table

The comparison of the measured and simulated pressure head profiles at all PMPs is shown in Fig. 2. Thus, the hydraulic model of the Ramnagar GSR WDN is calibrated with acceptable accuracy for pipe roughness values 129, 119, 94 and 79 of HDPE, DI, CI < 10 and CI > 10 pipes, respectively, and is ready for use.

Fig. 2
figure 2

Comparison of simulated pressure heads with those measured in the field after calibration

Full size image

Summary and conclusions

A study of the calibration of WDN using online data of flow and pressure is presented herein. The methodology uses pressure observations at few nodes for calibration. In the present study, the values of most of the input parameters were obtained accurately and only the pipe roughness coefficients were adjusted. The most critical input parameter is observed to be the valve opening. During calibration, all the valves were checked for their current status and settings. Hourly, observations of pressure values in the network were used to adjust pipe roughness coefficient values by grouping them based on material and year of installation. This resulted in a more general calibration. Throttled valves were modeled based on percentage opening by classifying them into different groups. A close match between the modeled and observed pressure values were obtained for the case study for the whole day observations with different demands. The entire process of data collection and calibration is described. The methodology can be repeated for any network.