Abstract
Geostatistical methods are one of the advanced techniques used for interpolation of groundwater quality data. The results obtained from geostatistics will be useful for decision makers to adopt suitable remedial measures to protect the quality of groundwater sources. Data used in this study were collected from 78 wells in Varamin plain aquifer located in southeast of Tehran, Iran, in 2013. Ordinary kriging method was used in this study to evaluate groundwater quality parameters. According to what has been mentioned in this paper, seven main quality parameters (i.e. total dissolved solids (TDS), sodium adsorption ratio (SAR), electrical conductivity (EC), sodium (Na+), total hardness (TH), chloride (Cl−) and sulfate (SO42−)), have been analyzed and interpreted by statistical and geostatistical methods. After data normalization by Nscore method in WinGslib software, variography as a geostatistical tool to define spatial regression was compiled and experimental variograms were plotted by GS+ software. Then, the best theoretical model was fitted to each variogram based on the minimum RSS. Cross validation method was used to determine the accuracy of the estimated data. Eventually, estimation maps of groundwater quality were prepared in WinGslib software and estimation variance map and estimation error map were presented to evaluate the quality of estimation in each estimated point. Results showed that kriging method is more accurate than the traditional interpolation methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Groundwater is the most important natural resource used for drinking by many people around the world, especially in arid and semi-arid areas. The resource cannot be optimally used and sustained unless the quality of groundwater is assessed. Having a clear view of groundwater quality, decision makers can plan and organize the operation and maintenance of groundwater resources in a much better way. In Iran, groundwater resources are not only the most important resources for drinking purpose, but also they are extensively used in agricultural, domestic and industrial sections (Sadat-Noori et al. 2014). Understanding the spatial and temporal variation of groundwater quality is a crucial aspect for applying the optimal management of groundwater resources. Reliable data are essential for assessing and monitoring groundwater quality, but in many cases data collection all over the area is time-consuming and not possible, so interpolation methods can save time and money significantly (Sahebjalal 2012).
Applied environmental sciences often deal with regionalized data with the purpose of investigating the behavior of one or more spatially distributed attributes. Geostatistics science provides a number of methods based on random functions theory, which are frequently used to estimate the value of a spatially measured variable at the unsampled places. The main subject regarding any geostatistical method is the evaluation of spatial correlations, through parametric classes of covariance and variogram functions, which present the spatial regression among a dataset based on the spatial variability of couple of points at the specific spatial distances (lags) (Barca et al. 2017). Geostatistics focuses on spatial and temporal varying phenomena and can be considered as a collection of numerical techniques dealing with the description of spatial properties, employing chiefly random models in a manner similar to the way in which time series analysis characterizes temporal data. It offers a way of describing the spatial continuity of natural phenomena and provides adaptations of classical regression techniques to take advantage of this continuity (Bohling 2005). In the previous decades, the accuracy of interpolation methods for predicting groundwater properties has been investigated in several studies. Some studies are presented in the following.
Istok and Cooper (1988) used the kriging method to estimate heavy metal concentration in groundwater and concluded that this method was the best estimator for spatial prediction of lead. Bardossy and Kundzewicz (1990) studied two geostatistical techniques, point kriging and the IRF-k, for detection of outliers in groundwater quality. Their results showed the usefulness of these methods to assess the groundwater quality. Das Gupta et al. (1995) investigated groundwater resource quality in a Bangkok aquifer by geostatistical methods, and their results showed the usefulness of applying this method to issues related to groundwater quality. D’Agostino et al. (1998) investigated the spatial and temporal variability of nitrate in groundwater via kriging and co-kriging methods. Finke et al. (2004) used simple kriging to estimate water surface changes in the Netherlands and introduced it as a suitable method for mapping water surface. Huysmans and Dassargues (2009) studied the application of geostatistics on modeling groundwater flow and transport in a cross-bedded aquifer in Belgium. Their study showed that geostatistics is a powerful tool to determine subsurface heterogeneity for hydrogeological applications in a wide range of complex geological environment by applying geostatistics tool to a real aquifer. Zehtabian et al. (2013) carried out a study to find the most appropriate interpolation techniques to assess the spatial relationship of groundwater quality parameters (EC, TDS and TH) in Garmsar, Iran. They applied common geostatistical methods including Co-kriging, global kriging as well as some deterministic methods and concluded that co-kriging is one of the best approaches.
In this study, kriging estimation maps have been prepared to assess the efficiency of the geostatistical methods. Also, a focus has been made on applying more accurate variogram models on the experimental variograms, and variogram parameters have been validated. It has also been emphasized on a practical application of estimation variance to assess the uncertainty, and residual analysis to evaluate the error distribution. Furthermore, error map of the kriging method has been prepared, indicating the prospective sampling patterns. Although many geoscience researchers have applied geostatistical techniques, especially in groundwater, in the present study the anisotropy has been defined more reliably and the kriging method has been improved compared to previous researches. Since groundwater management requires awareness of the quality variations in their resources, in this research the groundwater quality situation of the Varamin plain aquifer, Iran, has been assessed followed by attempts to study the spatial distribution to identify places with the best quality. Geostatistical method (ordinary kriging) has been applied to predict and estimate groundwater quality parameters, and the desired maps have been compiled more significantly.
Materials and methods
The study area
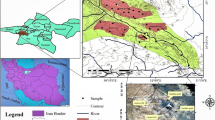
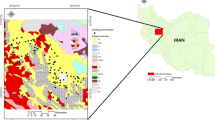
Varamin plain is located in southeast of the Tehran plain and northwest of central desert of Iran. This plain is located in the southern slopes of the Alborz Mountains, northern Iran. The study area is about 1535 km2. The Varamin plain is located between the longitudes of 51° 30′ and 51° 55′ and latitudes of 35° and 35° 38′ (Fig. 1). The average height of the plain is about 950 m above sea level. The annual average rainfall is about 172 mm and evaporation rate is about 2439 mm per year. The climate of this area is dry to semi-dry, but the southern part tends to be hot and dry due to its location in the desert border (Mokhtari and Espahbod 2009).
The main source of water in the Varamin plain is Jajrood River and groundwater sources are also considered as a significant source. Jajrood River is sometimes used for irrigation, while the groundwater is utilized for both drinking and irrigation purposes via pumping wells. The geological structures play an important role in the occurrence of groundwater in the plain. The Varamin aquifer is considered as a natural unconfined aquifer and is recharged across its entire surface by infiltrating rainfall and streams leaking into the subterranean system (Razandi et al. 2015). Based on the existence of two large anticlines, the aquifer is divided into the northern and southern parts. The northern part has more transmissibility and better water quality. From the northeast toward the southwest, both the quantity and quality of groundwater resources become more inappropriate. The Varamin plain has one major aquifer as well as several subsidiary aquifers in the central and southern parts. The rate of precipitation in this plain is very low, so it plays little role in recharging underground aquifers (Mollaie and Sorbi 2008).
As far as the geomorphological properties are concerned, the area is divided into the uplands, piedmont and plain. Uplands are located in the northeastern part of the region and its slope decreases toward the south. Piedmont areas are formed from old and new sediments. New sediments are in the form of an alluvial fan, and this aquifer has been formed on it. The northeastern part is formed from fine-grained and medium-grained particles. The northern uplands are formed from impenetrable and compressed formations; therefore, they have no influence on the storage of water (Mollaie and Sorbi 2008).
All of the groundwater samples were taken from the deepest parts of the wells with an average depth of about 85 m; however, they belonged to a mutual alluvium. Therefore, all the data are prepared from one groundwater system that its formation type is alluvial; as a result, the geostatistical method can show their correlation as well. In this study, 78 samples from the Iran Water Resources Management Company sampled in 2013 have been gathered to specify the groundwater quality of the Varamin plain aquifer. These wells are observation wells and the data of the Iran Water Resources Management Company are controlled during the field inspection of the observation wells on a monthly basis with an emphasis in the first half of the month.
Kriging method
Geoscientists often have to deal with spatial and modeling problems in the analyzing step of sparse data recorded from field observations. Geostatistics is an interesting tool used for describing and modeling spatial or temporal phenomena. Geostatistics provides a set of statistical tools for the analysis of data distributed in space and time domain. It allows the description of spatial patterns in a dataset, the incorporation of multiple sources of information in the mapping of features, the modeling of the spatial uncertainty and its propagation through decision making (Goovaerts 2014).
Kriging is a method for linear optimum unbiased interpolation with a minimum mean interpolation error. Furthermore, it is known to be an exact estimator in the sense that observation points are correctly re-estimated. This method does not necessarily require observation networks where data are normally distributed, and for the estimation of the structure of the regionalized variables, it considers only the neighboring points of estimation data (De Marsily 1986). The procedure facilitates the estimation at unsampled locations. Kriging estimates are calculated as weighted sums of the adjacent sampled concentrations. That is, if data appears to be highly continuous in spatial domain, the values closer to those estimated receive higher weights than those farther away (Ersoy et al. 2004).
One of the main advantages of kriging is that it presents the interpolation error of the values of the regionalized variable where there are no initial measurements. This feature offers a measure of the estimation accuracy and reliability of the spatial distribution of the variable (Theodossiou and Latinopoulos 2006). The spatial variability of a regionalized variable is described by a semi-variogram. The experimental semi-variogram is a graphical representation of the mean square variability between two neighboring points of distance h as shown in Eq. (1):
where \(\gamma (h)\) is the estimated value of the semi-variance for the h; N(h) is the number of experimental pairs separated by vector h; Z(x) and Z(x i + h) are values of the variable Z at the point x i and at a point of distance h from the point x i . At the experimental semi-variogram, a theoretical one is adjusted whose equation is derived based on the principle that kriging re-evaluates correctly the measurements at the observation points (Journel 1989).
Results and discussions
In this study, 78 data containing seven groundwater quality parameters sampled by the Iran Water Resources Management Company in 2013 were used to determine the groundwater quality of the Varamin plain. It must be investigated whether the data follow the normal distribution in advance. Since the aim is to apply ordinary kriging to map the parameters, identifying the statistical distribution of each parameter is of crucial importance, because ordinary kriging as a linear geostatistical tool will face biased results if the distribution of data does not follow the normal distribution. In this study, data were examined statistically with GS+ software. Since the data did not show normal distribution, they were normalized by the Nscore method in the WinGslib software. A statistical summary of the groundwater quality properties is given in Table 1. Histograms of the parameters drawn before and after the normalization process are shown in the appendix (Fig. 8). Normalization of data also validated based on the normalization index of W is as follows:
where W is the normalization index of data, S is skewness and K is kurtosis (Howarth and Earle 1979).
After data normalization, experimental variograms were prepared. Experimental variograms show spatial coherence of the data. It can also indicate the heterogeneity and anisotropy of the variable in the region. The best model for fitting a theoretical variogram was selected in GS+ software based on the minimum RSS and the maximum R2. If the sill or effective range is fluctuated in different directions, the studied region will show anisotropy. Interestingly, effective range and sill were relatively uniform after compiling the variograms in different directions. So, anisotropy was not observed in the study area. Figure 2 shows the directional variograms. Experimental variograms were fitted to the spherical models as the best theoretical variogram.
Table 2 shows the parameters of validated variograms obtained through groundwater quality. The ratio of nugget variance to sill is considered as a criterion for classifying the spatial dependence of groundwater quality variables. If this ratio is less than 0.25, the variables have strong spatial dependence; if the ratio is between 0.25 and 0.75, the variables indicate moderate spatial dependence; and if it is greater than 0.75, the variables show a weak spatial dependence (Mehrjardi et al. 2008). In this study, EC and TDS indicate moderate spatial dependence (0.36) and the other parameters show significant strong spatial structure. The effective range is estimated between 17.20 and 20.60 km for the parameters.
One of the advantages of kriging is the fact that it calculates the mean square interpolation error. Cross validation process is a step undertaken prior to geostatistical estimation to ensure the validity of the variogram parameters. Since nugget effect (C0), sill (C0 + C) and effective range (R) are used in kriging equation, it is important to assess how well these parameters can reproduce actual data. Before the implementation of any simulation or optimization mathematical model, its consistency with the original data must be verified. The proposed verification procedures do not aim to prove the correctness of the model, but to ensure the absence of systematic errors that could lead to biased estimations (Jolly et al. 2005). To determine the accuracy and validity of the process, the cross validation method was applied. In this method, the estimated values are plotted versus actual values. If the estimated values are equal to actual data, points will fall exactly on the line of the 45° (actual data = estimated data). More distribution points around the 45° line present the difference between the actual and predicted values. Figure 3 shows the cross validation of quality parameters via jackknife kriging. Also, to validate the models, some validation indicators, including mean error (ME), mean square error (MSE), mean square deviations ratio (MSDR), median square deviations ratio (MeSDR) and relative mean absolute error (RMAE) were applied and evaluated. Equations for the indicators are as follows:
where z(x i ) is the observed value at location x i , z*(x i ) is the predicted value at location x i and N is the number of pairs of observed and predicted values (Adhikary et al. 2011). The cross validation indicators are listed in Table 3.
Since a linear regression model is not always appropriate for the data, the accuracy of the model should be evaluated by defining residuals (actual data-estimated data) and examining residual plots. If the histogram of the residuals shows normal distribution with mean of zero, the accuracy of variogram parameters will be approved statistically (Rossi and Deutsch 2014). As seen in Fig. 4, histograms of the residual analysis show normal distribution.
Figure 5 shows the estimated 2D maps of the parameters, prepared in WinGslib1.5.7 software. Also, Fig. 9 (refer to the appendix) shows the estimated 3D maps, prepared in GS+ software. These maps clearly show that the quality of groundwater in the eastern half of the study area is very high. Also, the results show that a very small part in the southwest of the study area is exposed to contamination.
The estimation variances of kriging are independent of the value being estimated and are related only to the spatial position of the collected sample, the number of points and the variogram model. Given a set of values at the sampled locations, kriging is based on a variogram that summarizes how the variance of values at different points separated by a particular distance changes with distance. Estimation variance is a measure of confidence in predictions and is a function of the form of the variogram, the sample configuration and the sample support. It provides the information of regional variable in the regions with no recorded variable, and uncertainties can be evaluated with the parameters raised by the kriging method (Journel and Huijbregts 1978). As seen in Fig. 6, areas with a high estimation variance determine the area with high uncertainty of the estimation; therefore, these areas need to be sampled and studied further in prospective researches to decrease the uncertainty.
Since variance and spatial variance depend particularly on the dimension of measurements, a reasonable and credible judgment cannot be made only by these parameters. Quantifying errors allows researchers to qualify the uncertainty of the estimation method in a better way. Hence, defining a parameter which is independent of the dimension of data is certainly appreciated. Estimation error depends also on the estimated value, and it is the ratio of estimation of standard deviation to the estimated value in a block. However, determining a parameter arising from data which is independent from actual and estimated value may determine the uncertainties much better (Jalali et al. 2017). Figure 7 shows the error map of the estimated data for all the parameters.
Conclusions and summary
Seven parameters including TH, TDS, Cl−, SO42−, Na+, SAR and EC were utilized in this study to compile the groundwater quality. These parameters have significant influence on groundwater quality. The parameters had high skewness, so they were normalized by the Nscore method in WinGslib software to decrease the uncertainties raised from biased estimation. Then, the best model for fitting a theoretical variogram was determined in GS+ software based on the minimum RSS for each parameter. The spatial structure model was moderate for TDS and EC, and very strong for the other groundwater parameters, indicating high accuracy in interpolation. the cross validation process (jackknife and residual analysis) was performed to validate the variogram theoretical model. Then, groundwater quality maps of the aquifer were prepared and areas with low quality were identified. As the interpolated maps show, at the eastern half of the Varamin plain, groundwater quality is very high, and also a very small part in the southwestern of the study area is exposed to contamination. In the other parts of the aquifer, the groundwater quality is below the critical values.
Effective range was estimated between 17.20 and 20.60 km for all parameters. RSS for the parameters was very low, based on Table 2 introducing high accuracy of the fitted theoretical variograms. As it can be observed, the highest and lowest RSS were 0.24 and 0.16 for SAR and EC, respectively. The maximum values for ME and MSE were 0.01 and 0.52, based on Table 2. Also, the maximum and the minimum values for RMAE were 0.47 and 0.01 for EC and TH, respectively.
This paper has addressed an application of geostatistics to evaluate groundwater quality. Geostatistical methods are among the most appropriate tools to map the parameters in each block, because these techniques honor the spatial location of each sample and the interpolation maps are assigned by allocating geostatistical coefficient on each point. This study proved that the ordinary kriging is an appropriate method for estimating the values and producing reliable data and increasing the accuracy of assessment. It also saves financial and time resources. Since smoothing is one of the main problems of linear geostatistics, ordinary kriging in this research, other methods such as universal kriging and geostatistical simulations can be used to increase accuracy and evaluate results in future studies. Despite the smoothing drawback of kriging, this technique has been optimized by compiling the residual analysis and estimation variance procedures. Also, in this study, the errors related to variography have been minimized and has been carried out through cross validation, jackknife kriging, to assess the accuracy of the fitted theoretical model. In addition, estimation error map of the parameters was drawn to highlight the prospective sampling patterns. We hope our method can be useful in different regions with different data all over the world. This article may shed light on managing the hydrogeochemical quality of groundwater in several databases.
References
Adhikary PP, Dash CJ, Chandrasekharan H, Bej R (2011) Indicator and probability kriging methods for delineating Cu, Fe, and Mn contamination in groundwater of Najafgareh Block, Delhi, India. J Environ Monit Assess 176:663–676
Barca E, Porcu E, Bruno D, Passarella G (2017) An automated decision support system for aided assessment of variogram models. J Environ Model Softw 87:72–83
Bardossy A, Kundzewicz ZW (1990) Geostatistical methods for detection of outliers in groundwater quality spatial fields. J Hydrol 115:343–359
Bohling G (2005) Introduction to geostatistics and variogram analysis. Kansas Geological Survey, Lawrence, pp 1–20
D’Agostino V, Greene EA, Passarella G, Vurro M (1998) Spatial and temporal study of nitrate concentration in groundwater by means of co-regionalization. J Environ Geol 36:285–295
Das Gupta A, Jayakrishnan R, Onta PR, Ramnarong V (1995) Assessment of groundwater quality for the Bangkok aquifer system. In: Models for Assessing and Monitoring Groundwater Quality (Proceedings of a Boulder Symposium), IAHS Publication, p. 227
De Marsily G (1986) Quantitative hydrogeology; groundwater hydrology for engineers. Academic Press, Orlando, FL, p 440
Ersoy A, Yunsel TY, Cetin M (2004) Characterization of land contaminated by heavy metal mining using geostatistical methods. Arch Environ Contam Toxicol 46:162–175
Finke PA, Brus DJ, Bierkens MFP, Hoogland T, Knotters M, De Vries F (2004) Mapping groundwater dynamics using multiple sources of exhaustive high resolution data. J Geod 123:23–39
Goovaerts P (2014) The role of geostatistics in medical geology. In: 8th Congress of Ibérico on Geochemistry in EGU General Assembly (Abstracts), pp 17–22
Howarth RJ, Earle SAM (1979) Application of a generalized power transformation to geochemical data. J Int Assoc Math Geol 11:45–62
Huysmans M, Dassargues A (2009) Application of multiple-point geostatistics on modelling groundwater flow and transport in a cross-bedded aquifer (Belgium). Hydrogeol J. https://doi.org/10.1007/s10040-009-0495-2
Istok JD, Cooper RM (1988) Geostatistics applied to groundwater pollution. III: global estimates. J Environ Eng 114:915–928
Jalali M, Karami S, Marj AF (2017) On the problem of the spatial distribution delineation of the groundwater quality indicators via multivariate statistical and geostatistical approaches. J Environ Monit Assess (in press)
Jolly WM, Graham JM, Michaelis A, Nemani R, Running SW (2005) A flexible, integrated system for generating meteorological surfaces derived from point sources across multiple geographic scales. J Environ Model Softw 20:873–882
Journel AG (1989) Fundamentals of geostatistics in five lessons, short course in geology, vol 8. American Geophysical Union, Washington, DC, p 57
Journel AG, Huijbregts CJ (1978) Mining geostatistics. Academic Press, New York, p 600
Mehrjardi RT, Jahromi MZ, Mahmodi S, Heidari A (2008) Spatial distribution of groundwater quality with geostatistics (case study: yazd-Ardakan plain). World Applied Sci J 4:9–17
Mokhtari HR, Espahbod MR (2009) The investigation of hydrodynamic parameters potentiality of the Varamin Plain regarding the variation of salinity gradient. J Earth 4:27–47
Mollaie M, Sorbi A (2008) Investigate the quantitative situation of Varamin plain’s groundwater in a water 5-year period. In: Third conference of applied geology and environment, Islamshahr, Iran, Islamic Azad University of Islamshahr
Razandi Y, Pourghasemi HR, Neisani NS, Rahmati O (2015) Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using GIS. Earth Sci Inf 8:867–883
Rossi ME, Deutsch CV (2014) Mineral resource estimation. Springer, Dordrecht, p 337
Sadat-Noori SM, Ebrahimi K, Liaghat AM (2014) Groundwater quality assessment using the water quality index and GIS in Saveh-Nobaran aquifer, Iran. J Environ Earth Sci 71:3827–3843
Sahebjalal E (2012) Application of geostatistical analysis for evaluating variation in groundwater characteristics. J World Appl Sci 18:135–141
Theodossiou N, Latinopoulos P (2006) Evaluation and optimization of groundwater observation networks using the kriging methodology. J Environ Model Softw 21:991–1000
Zehtabian G, Azareh A, Samani AN, Rafei J (2013) Determining the most suitable geostatistical method to develop zoning map of parameters EC, TDS and TH groundwater (case study: garmsar Plain, Iran). Int J Agron Plant Prod 4:1855–1862
Acknowledgements
The authors would like to thank the Iran Water Resources Management Company for collecting, analyzing and providing the data. Also, the authors express their sincere appreciation and gratitude to Dr. Mohammad Jalali for his scientific contributions. Also, we fully appreciate the anonymous reviewers for their professional reviewing. Their precious comments have definitely improved the scientific quality of the paper. We thank the editorial board of the Journal of Applied Water Science for their consideration.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations’’
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Karami, S., Madani, H., Katibeh, H. et al. Assessment and modeling of the groundwater hydrogeochemical quality parameters via geostatistical approaches. Appl Water Sci 8, 23 (2018). https://doi.org/10.1007/s13201-018-0641-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s13201-018-0641-x